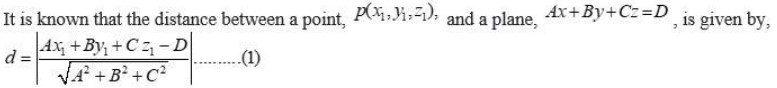Class 12 Maths Chapter 11 Three-Dimensional Geometry NCERT Solutions PDF Download

Q: 42. If the lines x−3−3=y−22k=z−32&x−13k=y−11=z−6−5 are perpendicular, find the value of k

The direction of ratios of the lines, x−3−3=y−22k=z−32&x−13k=y−11=z−6−5 , are −3, 2k, 2and3k, 1, −5 respectively. It is known that two lines with direction ratios, a1, b1, c1 and a2, b2, c2 , are perpendicular, if a1a2 + b1b2 + c1c2 =0 ∴−3 (3k)+2k×1+2 (−5)=0⇒−9k+2k−10=0⇒7k=−10⇒k=−107 Therefore, for k= -10/7, the given lines are perpendicular to each other.

Q: 29. Find the intercepts cut off by the plane 2x+y−z=5

2x+y−z=5 ......... (1) Dividing both sides of equation (1) by 5, we obtain 25x+y5−z5=1⇒x52+y5+z−5=1.......... (2) It is known that the equation of a plane in intercept form is xa+yb+zc=1 , where a, b, c are the intercepts cut off by the plane at x, y, and z axes respectively. Therefore, for the given equation, a=52, b=5andc=−5 Thus, the intercepts cut off by the plane are 52 , 5and−5.

Updated on Aug 7, 2025 12:06 IST

By Pallavi Pathak, Assistant Manager Content

In 3D Geometry Class 12, students will learn to use vector algebra in three-dimensional geometry. The chapter covers the direction ratios and direction cosines of a line joining two points, and equations of planes and lines in space under different conditions, distance of a point from a plane, shortest distance between two skew lines, angle between two planes, two lines, a plane, and a line.
3-Dimensional Geometry Class 12 NCERT solutions are given in a step-by-step format for students to understand the concepts deeply and prepare well for their CBSE Board examination and other competitive exams like JEE Mains. The students can also download the free Three-Dimensional Geometry Class 12 Solutions PDF from this page and improve their exam preparation.
To get access to the topic-wise revision PDF and notes of class 12 Maths, students must check - Class 12 Maths Notes PDF.

Table of content

Understanding 3D Geometry in Class 12 – A Brief Insight
Class 12 Three Dimensional Geometry: Key Topics, Weightage
Important Formulas of 3D Geometry Class 12
Download Class 12 Three-Dimensional Geometry NCERT Solution PDF for Free
Class 12 Three Dimensional Geometry Exercise-wise Solutions
Class 12 Three Dimensional Geometry Exercise 11.1 Solutions
NCERT Class 12 Math Chapter 11 Three Dimensional Geometry Solutions- FAQs

Understanding 3D Geometry in Class 12 – A Brief Insight

Here is a quick overview of the Class 12 3-Dimensional Geometry:

The chapter talks about the direction cosines of a line, which are defined as the line makes cosines of the angles with the positive directions of the coordinate axes.
If the direction cosines of a line are - l, m, and n, then - $l^{2} + m^{2} + n^{2} = 1$
The direction cosines of the line joining two points P(x1,y1,z1) and Q (x2,y2,z2) are - $\frac{x_{2} - x_{1}}{PQ}, \frac{y_{2} - y_{1}}{PQ}, \frac{z_{2} - z_{1}}{PQ}$
PQ = $PQ = \sqrt{{(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2} + {(z_{2} - z_{1})}^{2}}$
Direction ratios of a line are the numbers proportional to the direction cosines of a line.
The chapter also covers the skew lines concept, the angle between skew lines, and the shortest distance between two skew lines.

If you are looking for the CBSE short revision notes for Chemistry, Physics and Maths of Class 12, see here - NCERT Class 12 Notes.

Class 12 Three Dimensional Geometry: Key Topics, Weightage

Class 12 Three-Dimensional Geometry is an important chapter of Mathematics. Find below the topics covered in Chapter 11, Class 12 Maths:

Exercise	Topics Covered
11.1	Introduction
11.2	Direction Cosines and Direction Ratios of a Line
11.3	Equation of a Line in Space
11.4	Angle between Two Lines
11.5	Shortest Distance between Two Lines

3D Geometry Class 12 Weightage in JEE Mains

Exam	Number of Questions	Weightage
JEE Main	2 questions	6.6% to 8%

Important Formulas of 3D Geometry Class 12

Class 12 Chapter 11 Three-Dimensional Geometry Important Formulae for CBSE and Competitive Exams

Direction Cosines Relationship
$l^2 + m^2 + n^2 = 1$
Equation of a Line
- Vector form: $\vec{r} = \vec{a} + \lambda \vec{b}$
- Cartesian form: $\frac{x - x_1}{l} = \frac{y - y_1}{m} = \frac{z - z_1}{n}$
Equation of a Plane
- General form: $ax + by + cz + d = 0$
- Vector form: $\vec{r} \cdot \vec{n} = d$
Angle between Two Lines
$\cos \theta = \frac{\vec{b_1} \cdot \vec{b_2}}{|\vec{b_1}||\vec{b_2}|}$
Angle between Two Planes
$\cos \theta = \frac{|a_1a_2 + b_1b_2 + c_1c_2|}{\sqrt{a_1^2 + b_1^2 + c_1^2} \sqrt{a_2^2 + b_2^2 + c_2^2}}$
Distance of a Point from a Plane
$d = \frac{|ax_1 + by_1 + cz_1 + d|}{\sqrt{a^2 + b^2 + c^2}}$
Shortest Distance Between Two Skew Lines
$d = \frac{|\vec{b_1} \cdot (\vec{a_2} - \vec{a_1}) \times \vec{b_2}|}{|\vec{b_1} \times \vec{b_2}|}$
Condition for Coplanarity of Two Lines
$(\vec{a_2} - \vec{a_1}) \cdot (\vec{b_1} \times \vec{b_2}) = 0$

Download Class 12 Three-Dimensional Geometry NCERT Solution PDF for Free

Students must download the Three-Dimensional Geometry Class 12 Solutions PDF from the link given below. The well-structured solutions created by Shiksha's expert will help students to score high in the CBSE Board exam and entrance exams like JEE Mains.

Class 12 Math Chapter 10 Vector Solution PDF: Free PDF Download

Class 12 Three Dimensional Geometry Exercise-wise Solutions

Chapter 11 Three-dimensional geometry involves concepts such as Direction Cosines and Direction Ratios, the Equation of a Line, the Angle between a line and a plane, and others. Students must understand these topics to excel in board exams and competitive entrance tests.

Class 12 Three Dimensional Geometry Exercise 11.1 Solutions

Q1. If a line makes angles 90°, 135°, 45° with x ,y and z axes respectively, find its direction cosines.

A.1. Let the direction cosine of the line be l, m, n.

Then, $\begin{array}{l} l = 9 0^{\circ} = c o s 9 0^{\circ} = 0 \\ m = c o s 135 = \frac{- 1}{} \\ n = c o s 4 5^{\circ} = \frac{1}{} \end{array}$

Q2. Find the direction cosines of a line which makes equal angles with the co-ordinate axes.

A.2. Let the angles be α, β, r which are equal

Let the direction cosines of the line be l, m, n.

$\begin{array}{l} l = c o s α, m = c o s β, n = c o s r \\ α = β = r \\ l^{2} + m^{2} + n^{2} = 1 \\ c o s^{2} α + c o s^{2} β + c o s^{2} r = 1 \\ c o s^{2} α + c o s^{2} α + c o s^{2} α = 1 \\ 3 c o s^{2} α = 1 \\ c o s^{2} α = \frac{1}{3} \\ c o s α = \frac{1}{} \end{array}$

Q3. If a line has direction ratios −18, 12, −4, then what are its direction cosines?

A.3. Direction cosine are

$\begin{array}{l} \frac{- 18}{}, \frac{+ 12}{}, \frac{- 4}{} \\ = \frac{- 18}{22}, \frac{12}{22}, \frac{- 4}{22} \\ = \frac{- 9}{11}, \frac{6}{11}, \frac{- 2}{11} \end{array}$

Q4. Show that the points (2, 3, 4), (−1, −2, 1), (5, 8, 7) are collinear.

A.4. Given,

A(2,3,4), B(-1,-2,1), C(5,8,7)

Direction ratio of AB= $\begin{array}{l} (- 1 - 2), (- 2 - 3), (1 - 4) \\ = (3, - 5, - 3) \end{array}$

Where, a₁=3, b₁=-5, c₁=-3

Direction ratio of BC= $\begin{array}{l} (5 - (- 1)), (8 - (- 2)), (7 - 1) \\ = (6, 10, 6) \end{array}$

Where, a₂=6, b₂=10, c₂=6

Now,

$\begin{array}{l} \frac{a_{2}}{a_{1}} = \frac{6}{- 3} = - 2 \\ \frac{b_{2}}{b_{1}} = \frac{10}{- 5} = - 2 \\ \frac{c_{2}}{c_{1}} = \frac{6}{- 3} = - 2 \end{array}$

Here, direction ratio of two-line segments are proportional.

So, A, B, C are collinear.

Commonly asked questions

42. If the lines $\frac{x - 3}{- 3} = \frac{y - 2}{2 k} = \frac{z - 3}{2} & \frac{x - 1}{3 k} = \frac{y - 1}{1} = \frac{z - 6}{- 5}$ are perpendicular, find the value of k

The direction of ratios of the lines, $\frac{x - 3}{- 3} = \frac{y - 2}{2 k} = \frac{z - 3}{2} & \frac{x - 1}{3 k} = \frac{y - 1}{1} = \frac{z - 6}{- 5}$ , are $- 3, 2 k, 2 a n d 3 k, 1, - 5$ respectively.

It is known that two lines with direction ratios, $a_{1}, b_{1}, c_{1} a n d a_{2}, b_{2}, c_{2}$ , are perpendicular, if $a_{1} a_{2} + b_{1} b_{2} + c_{1} c_{2} = 0$

$\begin{array}{l} ∴ - 3 (3 k) + 2 k \times 1 + 2 (- 5) = 0 \\ \Rightarrow - 9 k + 2 k - 10 = 0 \\ \Rightarrow 7 k = - 10 \\ \Rightarrow k = \frac{- 10}{7} \end{array}$

Therefore, for k= -10/7, the given lines are perpendicular to each other.

46. Find the coordinates of the point where the line through $(5, 1, 6) a n d (3, 4, 1)$ crosses the YZ-plane.

It is known that the equation of the line passing through the points, $(x_{1}, y_{1}, z_{1}) a n d (x_{2}, y_{2}, z_{2}),$ is $\frac{x - x_{1}}{x_{2} - x_{1}} = \frac{x - y_{1}}{y_{2} - y_{1}} = \frac{z - z_{1}}{z_{2} - z_{1}}$

The line passing through the points, $(5, 1, 6) a n d (3, 4, 1),$ is given by,

$\begin{array}{l} \frac{x - 5}{3 - 5} = \frac{y - 1}{4 - 1} = \frac{z - 6}{1 - 6} \\ \Rightarrow \frac{x - 5}{- 2} = \frac{y - 1}{3} = \frac{z - 6}{- 5} = k (s a y) \\ \Rightarrow x = 5 - 2 k, y = 3 k + 1, z = 6 - 5 k \end{array}$

Any point on the line is of the form $(5 - 2 k, 3 k + 1, 6 - 5 k) .$

The equation of $Y Z - p l a n e i s x = 0$

Since the line passes through YZ-plane,

$5 - 2 k = 0$

$\begin{array}{l} \Rightarrow k = \frac{5}{2} \\ \Rightarrow 3 k + 1 = 3 \times \frac{5}{2} + 1 = \frac{17}{2} \\ 6 - 5 k = 6 - 5 \times \frac{5}{2} = \frac{- 13}{2} \end{array}$

Therefore, the required point is $(0, \frac{17}{2}, \frac{- 13}{2})$ .

30. Find the equation of the plane with intercept 3 on the y- axis and parallel to ZOX plane.

The equation of the plane ZOX is

y = 0

Any plane parallel to it is of the form, y = a

Since the y-intercept of the plane is 3,

∴ a = 3

Thus, the equation of the required plane is y = 3

29. Find the intercepts cut off by the plane $2 x + y - z = 5$

$2 x + y - z = 5 . . . . . . . . . (1)$

Dividing both sides of equation (1) by 5, we obtain

$\begin{array}{l} \frac{2}{5} x + \frac{y}{5} - \frac{z}{5} = 1 \\ \Rightarrow \frac{x}{\frac{5}{2}} + \frac{y}{5} + \frac{z}{- 5} = 1 . . . . . . . . . . (2) \end{array}$

It is known that the equation of a plane in intercept form is $\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1$ , where a, b, c are the intercepts cut off by the plane at x, y, and z axes respectively.

Therefore, for the given equation,

$a = \frac{5}{2}, b = 5 a n d c = - 5$

Thus, the intercepts cut off by the plane are $\frac{5}{2}$ $, 5 a n d - 5 .$

31. Find the equation of the plane through the intersection of the planes $3 x - y + 2 z - 4 = 0 a n d x +$ $y + z - 2 = 0$ and the point $(2, 2, 1) .$

The equation of any plane through the intersection of the planes,

$3 x - y + 2 z - 4 = 0 a n d x + y + z - 2 = 0,$ is

$(3 x - y + 2 z - 4) + α (x + y + z - 2) = 0, w h e r e, α \in R . . . . . . . . . . (1)$

The plane passes through the point $(2, 2, 1) .$ Therefore, this point will satisfy equation (1).

$\begin{array}{l} ∴ (3 \times 2 - 2 + 2 \times 1 - 4) + α (2 + 2 + 1 - 2) = 0 \\ \Rightarrow 2 + 3 α = 0 \\ \Rightarrow α = - \frac{2}{3} \end{array}$

Substituting $α = - \frac{2}{3}$ in equation (1), we obtain

$\begin{array}{l} (3 x - y + 2 z - 4) - \frac{2}{3} (x + y + z - 2) = 0 \\ \Rightarrow 3 (3 x - y + 2 z - 4) - 2 (x + y + z - 2) = 0 \\ \Rightarrow (9 x - 3 y + 6 z - 12) - 2 (x + y + z - 2) = 0 \\ \Rightarrow 7 x - 5 y + 4 z - 8 = 0 \end{array}$

40. Find the equation of the line parallel to x-axis and passing through the origin.

The line parallel to x-axis and passing through the origin is x-axis itself.

Let A be a point on x-axis. Therefore, the coordinates of A are given by $(a, 0, 0), w h e r e a ? R .$ Direction ratios of $O A a r e (a ? 0) = a, 0, 0$

The equation of OA is given by,

$\begin{array}{l} \frac{x ? 0}{a} = \frac{y ? 0}{0} = \frac{z ? 0}{0} \\ ? \frac{x}{1} = \frac{y}{0} = \frac{z}{0} = a \end{array}$

Thus, the equation of line parallel to x-axis and passing through origin is

$\frac{x}{1} = \frac{y}{0} = \frac{z}{0}$

41. If the coordinates of the points A, B, C, D be (1, 2, 3), (4, 5, 7), (−4, 3, −6) and (2, 9, 2) respectively, then find the angle between the lines AB and CD.

The coordinates of $A, B, C, a n d D a r e (1, 2, 3), (4, 5, 7), ( - 4, 3, - 6),$ and $(2, 9, 2)$ respectively.

The direction ratios of $A B a r e (4 - 1) = 3, (5 - 2) = 3, a n d (7 - 3) = 4$

The direction ratios of $C D a r e (2 - (- 4)) = 6, (9 - 3) = 6, a n d (2 - (- 6)) = 8$

It can be seen that, $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}} = \frac{1}{2}$

Therefore, AB is parallel to CD.

Thus, the angle between $A B a n d C D i s e i t h e r 0 ° o r 18$ $0$ $° .$

33. Find the vector equation of the plane passing through the intersection of the planes $\vec{r} . (2 \hat{i} + 2 \hat{j} - 2 \hat{k}) = 7, \vec{r} . (2 \hat{i} + 5 \hat{j} + 3 \hat{k}) = 9$ and through the point $(2, 1, 3) .$

The equations of the planes are $\vec{r} . (2 \hat{i} + 2 \hat{j} - 2 \hat{k}) = 7, \vec{r} . (2 \hat{i} + 5 \hat{j} + 3 \hat{k}) = 9$

$\begin{array}{l} \Rightarrow \vec{r} . (2 \hat{i} + 2 \hat{j} - 2 \hat{k}) - 7 = 0 . . . . . . . . . . (1) \\ \Rightarrow \vec{r} . (2 \hat{i} + 5 \hat{j} + 3 \hat{k}) - 9 = 0 . . . . . . . . . . (2) \end{array}$

The equation of any plane through the intersection of the planes given in equations (1) and (2) is given by,

$\begin{array}{l} [\vec{r} . (2 \hat{i} + 2 \hat{j} - 2 \hat{k}) - 7] + λ [\vec{r} . (2 \hat{i} + 5 \hat{j} + 3 \hat{k}) - 9] = 0, w h e r e, λ \in R \\ \vec{r} . [(2 \hat{i} + 2 \hat{j} - 2 \hat{k}) + λ (2 \hat{i} + 5 \hat{j} + 3 \hat{k})] = 9 λ + 7 \\ \vec{r} . [(2 + 2 λ) \hat{i} + (2 + 5 λ) \hat{j} + (3 λ - 3) \hat{k}] = 9 λ + 7 . . . . . . . . . . (3) \end{array}$

The plane passes through the point (2, 1, 3). Therefore, its position vector is given by,

$\vec{r} = 2 \hat{i} + 1 \hat{j} + 3 \hat{k}$

Substituting in equation (3), we obtain

$\begin{array}{l} (2 \hat{i} + \hat{j} + 3 \hat{k}) . [(2 + 2 λ) \hat{i} + (2 + 5 λ) \hat{j} + (3 λ - 3) \hat{k}] = 9 λ + 7 \\ \Rightarrow 2 (2 + 2 λ) + 1 (2 + 5 λ) + 3 (3 λ - 3) = 9 λ + 7 \\ \Rightarrow 4 + 4 λ + 2 + 5 λ + 9 λ - 9 = 9 λ + 7 \\ \Rightarrow 18 λ - 3 = 9 λ + 7 \\ \Rightarrow 9 λ = 10 \\ \Rightarrow λ = \frac{10}{9} \end{array}$

Substituting $λ = \frac{10}{9}$ in equation (3), we obtain

$\begin{array}{l} \vec{r} . (\frac{38}{9} \hat{i} + \frac{68}{9} \hat{j} + \frac{3}{9} \hat{k}) = 17 \\ \Rightarrow \vec{r} . (38 \hat{i} + 68 \hat{j} + 3 \hat{k}) = 153 \end{array}$

This is the vector equation of the required plane.

34. Find the equation of the plane through the line of intersection of the planes $x + y + z = 1 a n d 2 x + 3 y + 4 z = 5$ which is perpendicular to the plane $x - y + z = 0$

The equation of the plane through the intersection of the planes, $x + y + z = 1 a n d 2 x + 3 y + 4 z = 5$ , is

$(x + y + z - 1) + λ (2 x + 3 y + 4 z - 5)$

$\Rightarrow (2 λ + 1) x + (3 λ + 1) y + (4 λ + 1) z - (5 λ + 1) = 0 . . . . . . . . . . (1)$

The direction ratios, $a_{1}, b_{1}, c_{1},$ of this plane are $(2 λ + 1), (3 λ + 1), a n d (4 λ + 1) .$

The plane in equation (1) is perpendicular to $x - y + z = 0$

Its direction ratios, $a_{2}, b_{2}, c_{2},$ are $1, - 1, a n d 1$ .

Since the planes are perpendicular,

$\begin{array}{l} a_{1} a_{2} + b_{1} b_{2} + c_{1} c_{2} = 0 \\ \Rightarrow (2 λ + 1) - (3 λ + 1) + (4 λ + 1) = 0 \\ \Rightarrow 3 λ + 1 = 0 \\ \Rightarrow λ = - \frac{1}{3} \end{array}$

Substituting $λ = - \frac{1}{3}$ in equation (1), we obtain

$\begin{array}{l} \frac{1}{3} x - \frac{1}{3} z + \frac{2}{3} = 0 \\ \Rightarrow x - z + 2 = 0 \end{array}$

This is the required equation of the plane.

35. Find the angle between the planes whose vector equations are $\vec{r} . (2 \hat{i} + 2 \hat{j} - 3 \hat{k}) = 5 & \vec{r} . (3 \hat{i} - 3 \hat{j} + 5 \hat{k}) = 3$

The equations of the given planes are $\vec{r} . (2 \hat{i} + 2 \hat{j} - 3 \hat{k}) = 5 & \vec{r} . (3 \hat{i} - 3 \hat{j} + 5 \hat{k}) = 3$

It is known that if n1 and n2 are normal to the planes, $\vec{r} . \vec{n_{1}} = d_{1} & \vec{r} . \vec{n_{2}} = d_{2}$ then the angle between them, Q, is given by,

$c o s Q = | \frac{\vec{n_{1}} . \vec{n_{2}}}{| \vec{n_{1}} | | \vec{n_{2}} |} | . . . . . . . . . . (1)$

$\begin{array}{l} H e r e, \vec{n_{1}} = 2 \hat{i} + 2 \hat{j} - 3 \hat{k} & \vec{n_{2}} = 3 \hat{i} - 3 \hat{j} + 5 \hat{k} \\ ∴ \vec{n_{1}} . \vec{n_{2}} = (2 \hat{i} + 2 \hat{j} - 3 \hat{k}) (3 \hat{i} - 3 \hat{j} + 5 \hat{k}) = 2.3 + 2 . (- 3) + (- 3) . 5 = - 15 \\ | \vec{n_{1}} | = = \\ | \vec{n_{2}} | = = \end{array}$

Substituting the value of $\vec{n_{1}} . \vec{n_{2}}$ $| \vec{n_{1}} | & | \vec{n_{2}} |$ in equation (1), we obtain

$\begin{array}{l} c o s Q = | \frac{- 15}{.} | \\ \Rightarrow c o s Q = \frac{15}{} \\ \Rightarrow c o s Q^{- 1} = (\frac{15}{}) \end{array}$

36. In the following cases, determine whether the given planes are parallel or perpendicular and in case they are neither, find the angle between them.

$\begin{array}{l} \end{array} (a) 7 x + 5 y + 6 z + 30 = 0 a n d 3 x - y - 10 z + 4 = 0$

$(b) 2 x + y + 3 z - 2 = 0 a n d x - 2 y + 5 = 0$

$(c) 2 x - 2 y + 4 z + 5 = 0 a n d 3 x - 3 y + 6 z - 1$

$(d) 2 x - y + 3 z - 1 = 0 a n d 2 x - y + 3 z + 3 = 0$

$(e) 4 x + 8 y + z - 8 = 0 a n d y + z - 4 = 0$

The direction ratios of normal to the plane, $L_{1} : a_{1} x + b_{1} y + c_{1} z = 0 .$ , are $a_{1}, b_{1}, c_{1}$ and $L_{2} : a_{2} x + b_{2} y + c_{2} z = 0 .$

$L_{1}$
$\begin{array}{l} L_{2}, i f \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}} \\ L_{1} ⊥ L_{2}, i f a_{1} a_{2} + b_{1} b_{2} + c_{1} c_{2} = 0 \end{array}$

The angle between $L_{1} & L_{2}$ is given by,

(b) The equations of the planes are $2 x + y + 3 z - 2 = 0 a n d x - 2 y + 5 = 0$

$\begin{array}{l} a_{1} = 2, b_{1} = 1, c_{1} = 3 & a_{2} =, b_{2} = - 2, c_{2} = \\ a_{1} a_{2} + b_{1} b_{2} + c_{1} c_{2} = 2 \times 1 + 1 \times (- 2) + 3 \times 0 = 0 \end{array}$

Thus, the given planes are perpendicular to each other.

(c) The equations of the given planes are $2 x - 2 y + 4 z + 5 = 0 a n d 3 x - 3 y + 6 z - 1$

Here, $a_{1} = 2, b_{1} = - 2, c_{1} = 4 & a_{2} =, b_{2} = - 3, c_{2} = 6$

$a_{1} a_{2} + b_{1} b_{2} + c_{1} c_{2} = 2 \times 3 + 1 \times (- 2) (- 3) + 4 \times 6 = 6 + 6 + 24 = 36 \neq 0$

Thus, the given planes are not perpendicular to each other.

$\begin{array}{l} \frac{a_{1}}{a_{2}} = \frac{2}{3}, \frac{b_{1}}{b_{2}} = \frac{- 2}{- 3} = \frac{2}{3} & \frac{c_{1}}{c_{2}} = \frac{4}{6} = \frac{2}{3} \\ ∴ \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}} \end{array}$

Thus, the given planes are parallel to each other

(d) The equations of the planes are and $2 x - y + 3 z - 1 = 0 a n d 2 x - y + 3 z + 3 = 0$

$\begin{array}{l} a_{1} = 2, b_{1} = - 1, c_{1} = 3 & a_{2} =, b_{2} = - 1, c_{2} = 3 \\ \frac{a_{1}}{a_{2}} = \frac{2}{2} = 1, \frac{b_{1}}{b_{2}} = \frac{- 1}{- 1} = 1 & \frac{c_{1}}{c_{2}} = \frac{3}{3} = 1 \\ ∴ \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}} \end{array}$

Thus, the given lines are parallel to each other

(e) The equations of the given planes are $4 x + 8 y + z - 8 = 0 a n d y + z - 4 = 0$ $\begin{array}{l} a_{1} = 4, b_{1} = 8, c_{1} = 1 & a_{2} =, b_{2} = 1, c_{2} = 1 \\ a_{1} a_{2} + b_{1} b_{2} + c_{1} c_{2} = 4 \times 0 + 8 \times 1 + 1 = 9 \neq 0 \end{array}$

Therefore, the given lines are not perpendicular to each other.

$\begin{array}{l} \frac{a_{1}}{a_{2}} = \frac{4}{0}, \frac{b_{1}}{b_{2}} = \frac{8}{1} = 8 & \frac{c_{1}}{c_{2}} = \frac{1}{1} = 1 \\ ∴ \frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}} \end{array}$

Therefore, the given lines are not parallel to each other.

The angle between the planes is given by,

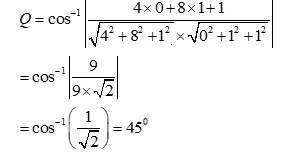
37. In the following cases find the distances of each of the given points from the corresponding given plane:

$\begin{array}{l} \end{array} (a) P o i n t (0, 0, 0) P l a n e 3 x - 4 y + 12 z = 3$

$(b) P o i n t (3, - 2, 1) P l a n e 2 x - y + 2 z + 3 = 0$

$c) P o i n t (2, 3, - 5) P l a n e x + 2 y - 2 z = 9$

$(d) P o i n t (- 6, 0, 0) P l a n e 2 x - 3 y + 6 z - 2 = 0$

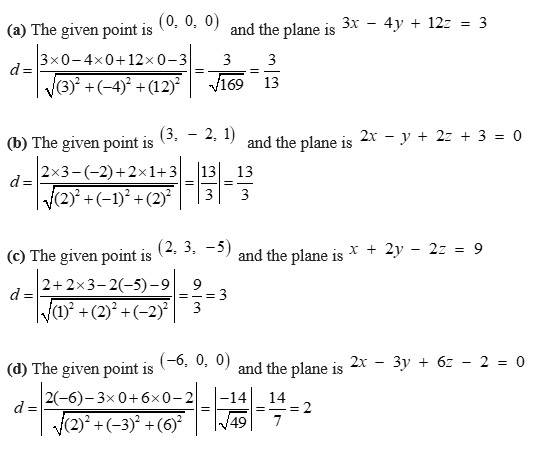
38. Show that the line joining the origin to the point $(2, 1, 1)$ is perpendicular to the line determined by the points $(3, 5, - 1), (4, 3, - 1) .$

Let OA be the line joining the origin, $O (0, 0, 0),$ and the point, $A (2, 1, 1) .$

Also, let BC be the line joining the points, $B (3, 5, - 1) a n d C (4, 3, - 1) .$

The direction ratios of $O A a r e 2, 1, a n d 1 a n d o f B C a r e (4 - 3) = 1, (3 - 5) = - 2, a n d (- 1 + 1) = 0$

OA is perpendicular to $B C, i f a_{1} a_{2} + b_{1} b_{2} + c_{1} c_{2} = 0$

$∴ a_{1} a_{2} + b_{1} b_{2} + c_{1} c_{2} = 2 \times 1 + 1 (- 2) + 1 \times 0 = 2 - 2 = 0$

Thus, OA is perpendicular to BC.

39. If $l_{1}, m_{1}, n_{1} a n d l_{2}, m_{2}, n_{2}$ are the direction cosines of two mutually perpendicular lines, show that the direction cosines of the line perpendicular to both of these are $m_{1} n_{2} - m_{2} n_{1}, n_{1} l_{2} - n_{2} l_{1}, l_{1} m_{2} - l_{2} m_{1} .$

It is given that $l_{1}, m_{1}, n_{1} a n d l_{2}, m_{2}, n_{2}$ are the direction cosines of two mutually perpendicular lines. Therefore,

$\begin{array}{l} l_{1} l_{2} + m_{1} m_{2} + n_{1} n_{2} = 0 . . . . . . . . . . (1) \\ {l_{1}}^{2} + {m_{1}}^{2} + n_{1}^{2} = 1 . . . . . . . . . . (2) \\ {l_{2}}^{2} + {m_{2}}^{2} + n_{2}^{2} = 1 . . . . . . . . . . (3) \end{array}$

Let $l, m, n$ be the direction cosines of the line which is perpendicular to the line with direction cosines $l_{1}, m_{1}, n_{1} a n d l_{2}, m_{2}, n_{2} .$

$\begin{array}{l} ∴ l l_{1} + m m_{1} + n n_{1} = 0 \\ l l_{2} + m m_{2} + n n_{2} = 0 \\ ∴ \frac{l}{m_{1} n_{2} - m_{2} n_{1}} = \frac{m}{n_{1} l_{2} - n_{2} l_{1}} = \frac{n}{l_{1} m_{2} - l_{2} m_{1}} \\ \Rightarrow \frac{l^{2}}{{(m_{1} n_{2} - m_{2} n_{1})}^{2}} = \frac{m^{2}}{{(n_{1} l_{2} - n_{2} l_{1})}^{2}} = \frac{n^{2}}{{(l_{1} m_{2} - l_{2} m_{1})}^{2}} \\ \Rightarrow \frac{l^{2}}{{(m_{1} n_{2} - m_{2} n_{1})}^{2}} = \frac{m^{2}}{{(n_{1} l_{2} - n_{2} l_{1})}^{2}} = \frac{n^{2}}{{(l_{1} m_{2} - l_{2} m_{2})}^{2}} \\ = \frac{l^{2} + m^{2} + n^{2}}{{(m_{1} n_{2} - m_{2} n_{1})}^{2} + {(n_{1} l_{2} - n_{2} l_{1})}^{2} + {(l_{1} m_{2} - l_{2} m_{2})}^{2}} . . . . . . . . . . (4) \end{array}$

$l, m, n$ are the direction cosines of the line.

$∴ l^{2} + m^{2} + n^{2} = 1 \dots (5)$

It is known that,

$\begin{array}{l} ({l_{1}}^{2} + {m_{1}}^{2} + n_{1}^{2}) ({l_{2}}^{2} + {m_{2}}^{2} + n_{2}^{2}) - {(l_{1} l_{2} + m_{1} m_{2} + n_{1} n_{2})}^{2} \\ = {(m_{1} n_{2} - m_{2} n_{1})}^{2} + {(n_{1} l_{2} - n_{2} l_{1})}^{2} + {(l_{1} m_{2} - l_{2} m_{1})}^{2} \\ F r o m, (1), (2) & (3), w e . o b t a i n \\ \Rightarrow 1.1 - 0 = {(m_{1} n_{2} - m_{2} n_{1})}^{2} + {(n_{1} l_{2} - n_{2} l_{1})}^{2} + {(l_{1} m_{2} - l_{2} m_{1})}^{2} \\ ∴ {(m_{1} n_{2} - m_{2} n_{1})}^{2} + {(n_{1} l_{2} - n_{2} l_{1})}^{2} + {(l_{1} m_{2} - l_{2} m_{1})}^{2} = 1 . . . . . . . . . . (6) \end{array}$

Substituting the values from equations (5) and (6) in equation (4), we obtain

$\frac{l^{2}}{{(m_{1} n_{2} - m_{2} n_{1})}^{2}} = \frac{m^{2}}{{(n_{1} l_{2} - n_{2} l_{1})}^{2}} = \frac{n^{2}}{{(l_{1} m_{2} - l_{2} m_{1})}^{2}} = 1$

Thus, the direction cosines of the required line are $m_{1} n_{2} - m_{2} n_{1}, n_{1} l_{2} - n_{2} l_{1}, l_{1} m_{2} - l_{2} m_{1}$

43. Find the vector equation of the line passing through $(1, 2, 3)$ and perpendicular to the plane

$\vec{r} = (\hat{i} + 2 \hat{j} - 5 \hat{k}) + 9 = 0$

The position vector of the point $(1, 2, 3)$ is $\vec{r} = \hat{i} + 2 \hat{j} + 3 \hat{k}$

The direction ratios of the normal to the plane, $\vec{r} = (\hat{i} + 2 \hat{j} - 5 \hat{k}) + 9 = 0$ , are $1, 2, a n d - 5$ and the normal vector is $\vec{N} = (\hat{i} + 2 \hat{j} - 5 \hat{k})$

The equation of a line passing through a point and perpendicular to the given plane is given by,

$\vec{l} = \vec{r} + λ \vec{N}, λ \in R \Rightarrow \vec{l} = (\hat{i} + 2 \hat{j} + 3 \hat{k}) + λ (\hat{i} + 2 \hat{j} - 5 \hat{k})$

44. Find the equation of the plane passing through $(a, b, c)$ and parallel to the plane $\vec{r} . (\hat{i} + \hat{j} + \hat{k}) = 2$

Any plane parallel to the plane, $\vec{r} . (\hat{i} + \hat{j} + \hat{k}) = 2$ , is of the form $\vec{r} . (\hat{i} + \hat{j} + \hat{k}) = λ . . . . . . . . . (1)$

The plane passes through the point (a, b, c). Therefore, the position vector $\vec{r}$ of this point is $\vec{r} = a \hat{i} + b \hat{j} + c \hat{k}$

Therefore, equation (1) becomes

$\begin{array}{l} (a \hat{i} + b \hat{j} + c \hat{k}) . (\hat{i} + \hat{j} + \hat{k}) = λ \\ \Rightarrow a + b + c = λ \end{array}$

Substituting $λ = a + b + c$ in equation (1), we obtain

$\vec{r} = (\hat{i} + \hat{j} + \hat{k}) = a + b + c . . . . . . . . . (2)$

This is the vector equation of the required plane.

Substituting $\vec{r} = x \hat{i} + y \hat{j} + z \hat{k}$ in equation (2), we obtain

$\begin{array}{l} (x \hat{i} + y \hat{j} + z \hat{k}) . (\hat{i} + \hat{j} + \hat{k}) = a + b + c \\ \Rightarrow x + y + z = a + b + c \end{array}$

45. Find the shortest distance between lines $\vec{r} = 6 \hat{i} + 2 \hat{j} + 2 \hat{k} + λ (\hat{i} - 2 \hat{j} - 2 \hat{k}) & \vec{r} = - 4 \hat{i} - \hat{k} + μ (3 \hat{i} - 2 \hat{j} - 2 \hat{k})$

The given lines are $\begin{array}{l} \vec{r} = 6 \hat{i} + 2 \hat{j} + 2 \hat{k} + λ (\hat{i} - 2 \hat{j} - 2 \hat{k}) . . . . . . . . . . (1) \\ \vec{r} = - 4 \hat{i} - \hat{k} + μ (3 \hat{i} - 2 \hat{j} - 2 \hat{k}) . . . . . . . . . . . (2) \end{array}$ $\begin{array}{l} \vec{r} = 6 \hat{i} + 2 \hat{j} + 2 \hat{k} + λ (\hat{i} - 2 \hat{j} - 2 \hat{k}) . . . . . . . . . . (1) \\ \vec{r} = - 4 \hat{i} - \hat{k} + μ (3 \hat{i} - 2 \hat{j} - 2 \hat{k}) . . . . . . . . . . . (2) \end{array}$

It is known that the shortest distance between two lines, $\vec{r} = a_{1} + λ b_{1} & \vec{r} = a_{2} + λ b_{2}$ is given by

$d = | \frac{(b_{1} \times b_{2}) . (a_{1} - a_{2})}{| b_{1} \times b_{2} |} |$

Comparing $\vec{r} = a_{1} + λ b_{1} & \vec{r} = a_{2} + λ b_{2}$ to equations (1) and (2), we obtain

$\begin{array}{l} \vec{a_{1}} = 6 \hat{i} + 2 \hat{j} + 2 \hat{k} \\ \vec{b_{1}} = \hat{i} - 2 \hat{j} - 2 \hat{k} \\ \vec{a_{2}} = - 4 \hat{i} - \hat{k} \\ \vec{b_{2}} = 3 \hat{i} - 2 \hat{j} - 2 \hat{k} \end{array}$

$\Rightarrow \vec{a_{2}} - \vec{a_{1}} = (- 4 \hat{i} - \hat{k}) - (6 \hat{i} + 2 \hat{j} + 2 \hat{k}) = 10 \hat{i} - 2 \hat{j} - 3 \hat{k}$

$\Rightarrow \vec{b_{1}} \times \vec{b_{2}} = | \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & - 2 & 2 \\ 3 & - 2 & - 2 \end{matrix} | = (4 + 4) \hat{i} - (- 2 - 6) \hat{j} + (- 2 + 6) \hat{k} = 8 \hat{i} + 8 \hat{j} + 4 \hat{k}$

$\begin{array}{l} ∴ | \vec{b_{1}} \times \vec{b_{2}} | = = 12 \\ (\vec{b_{1}} \times \vec{b_{2}}) . (\vec{a_{2}} - \vec{a_{1}}) = (8 \hat{i} + 8 \hat{j} + 4 \hat{k}) . (10 \hat{i} - 2 \hat{j} - 3 \hat{k}) = - 80 - 16 - 12 = - 108 \end{array}$

Substituting all the values in equation (1), we obtain

$d = | \frac{- 108}{12} | = 9$

Therefore, the shortest distance between the two given lines is 9 units.

47. Find the coordinates of the point where the line through (5, 1, 6) and (3, 4, 1) crosses the ZX-plane.

The line passing through the points, $(5, 1, 6) a n d (3, 4, 1),$ is given by,

Any point on the line is of the form $(5 - 2 k, 3 k + 1, 6 - 5 k) .$

Since the line passes through ZX-plane,

$\begin{array}{l} 3 k + 1 = 0 \\ \Rightarrow k = - \frac{1}{3} \\ \Rightarrow 5 - 2 k = 5 - 2 (- \frac{1}{3}) = \frac{17}{3} \\ 6 - 5 k = 6 - 5 (- \frac{1}{3}) = \frac{23}{3} \end{array}$

Therefore, the required point is $(\frac{17}{3}, 0, \frac{23}{3})$

48. Find the coordinates of the point where the line through $(3, - 4, - 5) a n d (2, - 3, 1)$ crosses the plane $2 x + y + z = 7) .$

It is known that the equation of the line through the points, $(x_{1}, y_{1}, z_{1}) a n d (x_{2}, y_{2}, z_{2})$ , is

$\frac{x - x_{1}}{x_{2} - x_{1}} = \frac{x - y_{1}}{y_{2} - y_{1}} = \frac{z - z_{1}}{z_{2} - z_{1}}$

Since the line passes through the points, $(3, - 4, - 5) a n d (2, - 3, 1)$ , its equation is given by,

$\begin{array}{l} \frac{x - 3}{2 - 3} = \frac{y + 4}{- 3 + 4} = \frac{z + 5}{1 + 5} \\ \Rightarrow \frac{x - 3}{- 1} = \frac{y + 4}{1} = \frac{z + 5}{6} = k (s a y) \\ \Rightarrow x = 3 - k, y = k - 4, z = 6 k - 5 \end{array}$

Therefore, any point on the line is of the form $(3 - k, k - 4, 6 k - 5) .$

This point lies on the plane, $2 x + y + z = 7$

$\begin{array}{l} ∴ 2 (3 - k) + (k - 4) + (6 k - 5) = 7 & 5 k - 3 = 7 & k = 2 \end{array}$

Hence, the coordinates of the required point are $(3 - 2, 2 - 4, 6 \times 2 - 5) i . e .,$ $(1, - 2, 7) .$

49. Find the equation of the plane passing through the point $(- 1, 3, 2)$ and perpendicular to each of the planes $x + 2 y + 3 z = 5 a n d 3 x + 3 y + z = 0 .$

The equation of the plane passing through the point $a (x + 1) + b (y - 3) + c (z - 2) = 0 \dots (1)$ where, a, b, c are the direction ratios of normal to the plane.

It is known that two planes, $a_{1} x + b_{1} y + c_{1} z + d_{1} = 0 & a_{2} x + b_{2} y + c_{2} z + d_{2} = 0$ are perpendicular, if $a_{1} a_{2} + b_{1} b_{2} + c_{1} c_{2} = 0$

Plane (1) is perpendicular to the plane, $x + 2 y + 3 z = 5$

$\begin{array}{l} a . 1 + b . 2 + c . 3 = 0 & a + 2 b + 3 c = 0 . . . . (2) \end{array}$

Also, plane (1) is perpendicular to the plane, $3 x + 3 y + z = 0$

$\begin{array}{l} a . 3 + b . 3 + c . 1 = 0 & 3 a + 3 b + c = 0 . . . . . (3) \end{array}$

From equations (2) and (3), we obtain

$\begin{array}{l} \frac{a}{2 \times 1 - 3 \times 3} = \frac{b}{3 \times 3 - 1 \times 1} = \frac{c}{1 \times 3 - 2 \times 3} \\ \Rightarrow \frac{a}{- 7} = \frac{b}{8} = \frac{c}{- 3} = k (s a y) \\ \Rightarrow a = - 7 k, b = 8 k, c = - 3 k \end{array}$

Substituting the values of a, b, and c in equation (1), we obtain

$\begin{array}{l} - 7 k (x + 1) + 8 k (y - 3) - 3 k (z - 2) = 0 \\ \Rightarrow (- 7 x - 7) + (8 y - 24) - 3 z + 6 = 0 \\ \Rightarrow - 7 x + 8 y - 3 z - 25 = 0 \\ \Rightarrow 7 x - 8 y + 3 z + 25 = 0 \end{array}$

This is the required equation of the plane.

50. If the points $(1, 1, p) a n d (- 3, 0, 1)$ be equidistant from the plane $\vec{r} . (3 \hat{i} + 4 \hat{j} - 12 \hat{k}) + 13 = 0$ then find the value of p

The position vector through the point $(1, 1, p)$ is $\vec{a_{1}} = \hat{i} + \hat{j} + p \hat{k}$

Similarly, the position vector through the point $(- 3, 0, 1)$ is

$\vec{a_{2}} = - 4 \hat{i} + \hat{k}$

The equation of the given plane is $\vec{r} . (3 \hat{i} + 4 \hat{j} - 12 \hat{k}) + 13 = 0$

It is known that the perpendicular distance between a point whose position vector is $\vec{a}$ and the plane, $\vec{r} . \vec{N} = d$ is given by, $D = \frac{| \vec{a} . \vec{N} - d |}{| \vec{N} |}$

Here, $\vec{N} = 3 \hat{i} + 4 \hat{j} - 12 \hat{k}$ and $d = - 13$

Therefore, the distance between the point (1, 1, p) and the given plane is

$\begin{array}{l} D_{1} = \frac{| (\hat{i} + \hat{j} + p \hat{k}) . (3 \hat{i} + 4 \hat{j} - 12 \hat{k}) + 13 |}{| 3 \hat{i} + 4 \hat{j} - 12 \hat{k} |} \\ \Rightarrow D_{1} = \frac{| 3 + 4 - 12 p + 13 |}{} \\ \Rightarrow D_{1} = \frac{| 20 - 12 p |}{13} . . . . . . . . . . (1) \end{array}$

Similarly, the distance between the point $(- 3, 0, 1)$ and the given plane is

$\begin{array}{l} D_{2} = \frac{| (3 \hat{i} + \hat{k}) . (3 \hat{i} + 4 \hat{j} - 12 \hat{k}) + 13 |}{| 3 \hat{i} + 4 \hat{j} - 12 \hat{k} |} \\ \Rightarrow D_{1} = \frac{| - 9 - 12 + 13 |}{} \\ \Rightarrow D_{1} = \frac{8}{13} . . . . . . . . . . (2) \end{array}$

It is given that the distance between the required plane and the points, $(1, 1, p) a n d (- 3, 0, 1),$ is equal.

$∴ D_{1} = D_{2}$

$\begin{array}{l} \Rightarrow \frac{| 20 - 12 p |}{13} = \frac{8}{13} \\ \Rightarrow 20 - 12 p = 8, o r, - (- 20 - 12 p) = 8 \\ \Rightarrow 12 p = 12, o r, 12 p = 28 \\ \Rightarrow p = 1, o r, p = \frac{7}{3} \end{array}$

51. Find the equation of the plane passing through the line of intersection of the planes $\vec{r} . (\hat{i} + \hat{j} + \hat{k}) = 1 & \vec{r} . (2 \hat{i} + 3 \hat{j} - \hat{k}) + 4 = 0$ and parallel to x - axis.

Equation of one plane is

$\begin{array}{l} \vec{r} . (\hat{i} + \hat{j} + \hat{k}) = 1 \\ \Rightarrow \vec{r} . (\hat{i} + \hat{j} + \hat{k}) - 1 = 0 \\ \vec{r} . (2 \hat{i} + 3 \hat{j} - \hat{k}) + 4 = 0 \end{array}$

The equation of any plane passing through the line of intersection of these planes is

$\begin{array}{l} [\vec{r} . (\hat{i} + \hat{j} + \hat{k}) - 1] + λ [\vec{r} . (2 \hat{i} + 3 \hat{j} - \hat{k}) + 4] = 0 \\ \vec{r} . [(2 λ + 1) \hat{i} + (3 λ + 1) \hat{j} + (1 - λ) \hat{k}] + (4 λ - 1) = 0 . . . . . (1) \end{array}$

Its direction ratios are (2λ + 1), (3λ + 1), and (1 − λ).

The required plane is parallel to x-axis. Therefore, its normal is perpendicular to x-axis.

The direction ratios of x-axis are 1, 0, and 0.

$\begin{array}{l} ∴ 1 . (2 λ + 1) + 0 (3 λ + 1) + 0 (1 - λ) = 0 \\ \Rightarrow 2 λ + 1 = 0 \\ \Rightarrow λ = - \frac{1}{2} \end{array}$

Substituting λ = -1/2 in equation (1), we obtain

$\begin{array}{l} \Rightarrow \vec{r} . [- \frac{1}{2} \hat{j} + \frac{3}{2} \hat{k}] + (- 3) = 0 \\ \Rightarrow \vec{r} (\hat{j} - 3 \hat{k}) + 6 = 0 \end{array}$

Therefore, its Cartesian equation is y − 3z + 6 = 0

This is the equation of the required plane.

52. If O be the origin and the coordinates of P be (1, 2, −3), then find the equation of the plane passing through P and perpendicular to OP.

The coordinates of the points, O and P, are (0, 0) and (1, 2, −3) respectively.

Therefore, the direction ratios of OP are (1 − 0) = 1, (2 − 0) = 2, and (−3 − 0) = −3

It is known that the equation of the plane passing through the point (x1, y1 z1) is

$a (x - x_{1}) + b (y - y_{1}) + c (z - z_{1}) = 0$ where, a, b, and c are the direction ratios of normal.

Here, the direction ratios of normal are 1, 2, and −3 and the point P is (1, 2, −3).

Thus, the equation of the required plane is

$\begin{array}{l} \end{array}$ $\begin{array}{l} 1 (x - 1) + 2 (y - 2) - 3 (z + 3) 0 & \Rightarrow x + 2 y - 3 z - 14 = 0 \end{array}$

53. Find the equation of the plane which contains the line of intersection of the planes $\vec{r} (\hat{i} + 2 \hat{j} + 3 \hat{k}) - 4 = 0, \vec{r} . (2 \hat{i} + h t \hat{j} - \hat{k}) + 5 = 0$ and which is perpendicular to the plane $\vec{r} . (5 \hat{i} + 3 \hat{j} - 6 \hat{k}) + 8 = 0$

The equations of the given planes are

$\begin{array}{l} \vec{r} . (\hat{i} + 2 \hat{j} + 3 \hat{k}) - 4 = 0 . . . . . (1) \\ \vec{r} . (2 \hat{i} + \hat{j} - \hat{k}) + 5 = 0 . . . . . . (2) \end{array}$

The equation of the plane passing through the line intersection of the plane given in equation (1) and equation (2) is

$\begin{array}{l} [\vec{r} . (\hat{i} + 2 \hat{j} + 3 \hat{k}) - 4] + λ [\vec{r} . (2 \hat{i} + \hat{j} - \hat{k}) + 5] = 0 \\ \vec{r} . [(2 λ + 1) \hat{i} + (λ + 2) \hat{j} + (3 - λ) \hat{k}] + (5 λ - 4) = 0 . . . . . (3) \end{array}$

The plane in equation (3) is perpendicular to the plane, $\vec{r} . (5 \hat{i} + 3 \hat{j} - 6 \hat{k}) + 8 = 0$

$\begin{array}{l} ∴ 5 (2 λ + 1) + 3 (λ + 2) - 6 (3 - λ) = 0 \\ \Rightarrow 19 λ - 7 = 0 \\ \Rightarrow λ = \frac{7}{19} \end{array}$

Substituting λ = 7/19 in equation (3), we obtain

$\begin{array}{l} \Rightarrow \vec{r} . (\frac{13}{19} \hat{i} + \frac{45}{19} \hat{j} + \frac{50}{19} \hat{k}) \frac{- 41}{19} = 0 \\ \Rightarrow \vec{r} . (33 \hat{i} + 45 \hat{j} + 50 \hat{k}) - 41 = 0 \end{array}$

This is the vector equation of the required plane.

The Cartesian equation of this plane can be obtained by substituting $\vec{r} = x \hat{i} + y \hat{j} + z \hat{k}$ in equation (3).

$\begin{array}{l} (x \hat{i} + y \hat{j} + z \hat{k}) . (33 \hat{i} + 45 \hat{j} + 50 \hat{k}) - 41 = 0 \\ \Rightarrow 33 x + 45 y + 50 z - 41 = 0 \end{array}$

55. Find the vector equation of the line passing through (1, 2, 3) and parallel to the plane $\vec{r} = (\hat{i} - \hat{j} + 2 \hat{k}) = 5$ and $\vec{r} . (3 \hat{i} + \hat{j} + \hat{k}) = 6$

Let the required line be parallel to vector $\vec{b}$ given by,

$\vec{b} = b_{1} \hat{i} + b_{2} \hat{j} + b_{3} \hat{k}$

The position vector of the point (1, 2, 3) is $\vec{a} = \hat{i} + 2 \hat{j} + 3 \hat{k}$

The equation of line passing through (1, 2, 3) and parallel to $\vec{b}$ is given by,

$\begin{array}{l} \vec{r} = \vec{a} + λ \vec{b} \\ \Rightarrow \vec{r} (\hat{i} + 2 \hat{j} + 3 \hat{k}) + λ (b_{1} \hat{i} + b_{2} \hat{j} + b_{3} \hat{k}) . . . . . . . . (1) \end{array}$

The equations of the given planes are

$\begin{array}{l} \vec{r} = (\hat{i} - \hat{j} + 2 \hat{k}) = 5 . . . . . . . . (2) \\ \vec{r} . (3 \hat{i} + \hat{j} + \hat{k}) = 6 . . . . . . . . (3) \end{array}$

The line in equation (1) and plane in equation (2) are parallel. Therefore, the normal to the plane of equation (2) and the given line are perpendicular.

$\begin{array}{l} \Rightarrow (\hat{i} - \hat{j} + 2 \hat{k}) . λ (b_{1} \hat{i} + b_{2} \hat{j} + b_{3} \hat{k}) = 0 \\ \Rightarrow λ (b_{1} - b_{2} + 2 b_{3}) = 0 \\ \Rightarrow b_{1} - b_{2} + 2 b_{3} = 0 . . . . . . . . . . (4) \end{array}$

Similarly, $(3 \hat{i} + \hat{j} + \hat{k}) . λ (b_{1} \hat{i} + b_{2} \hat{j} + b_{3} \hat{k}) = 0$

From equations (4) and (5), we obtain

$\begin{array}{l} \frac{b_{1}}{(- 1) \times 1 - 1 \times 2} = \frac{b_{2}}{2 \times 3 - 1 \times 1} = \frac{b_{3}}{1 \times 1 - 3 \times (- 1)} \\ \Rightarrow \frac{b_{1}}{- 3} = \frac{b_{2}}{5} = \frac{b_{3}}{4} \end{array}$

Therefore, the direction ratios of $\vec{b}$ are −3, 5, and 4.

$∴ \vec{b} = b_{1} \hat{i} + b_{2} \hat{j} + b_{3} \hat{k} = - 3 \hat{i} + 5 \hat{j} + 4 \hat{k}$

Substituting the value of $\vec{b}$ in equation (1), we obtain

$\vec{r} = (\hat{i} + 2 \hat{j} + 3 \hat{k}) + λ (- 3 \hat{i} + 5 \hat{j} + 4 \hat{k})$

This is the equation of the required line.

56. Find the vector equation of the line passing through the point (1, 2, − 4) and perpendicular to the two lines:

$\frac{x - 8}{3} = \frac{y + 19}{- 16} = \frac{z - 10}{7}$ and $\frac{x - 15}{3} = \frac{y - 29}{8} = \frac{z - 5}{- 5}$

Let the required line be parallel to the vector $\vec{b}$ given by, $\vec{b} = b_{1} \hat{i} + b_{2} \hat{j} + b_{3} \hat{k}$

The position vector of the point (1, 2, − 4) is $\vec{a} = \hat{i} + 2 \hat{j} - 4 \hat{k}$

The equation of the line passing through (1, 2, −4) and parallel to vector $\vec{b}$ is

$\begin{array}{l} \vec{r} = \vec{a} + λ \vec{b} \\ \Rightarrow \vec{r} = (\hat{i} + 2 \hat{j} - 4 \hat{k}) + λ (b_{1} \hat{i} + b_{2} \hat{j} + b_{3} \hat{k}) . . . . . . . (1) \end{array}$

The equations of the lines are

$\begin{array}{l} \frac{x - 8}{3} = \frac{y + 19}{- 16} = \frac{z - 10}{7} . . . . . . . . (2) \\ \frac{x - 15}{3} = \frac{y - 29}{8} = \frac{z - 5}{- 5} . . . . . . . . (3) \end{array}$

Line (1) and line (2) are perpendicular to each other.

$∴ 3 b_{1} - 16 b_{2} + 7 b_{3} = 0 . . . . . . . . (4)$

Also, line (1) and line (3) are perpendicular to each other.

$∴ 3 b_{1} + 8 b_{2} - 5 b_{3} = 0 . . . . . . . . (5)$

From equations (4) and (5), we obtain

$\begin{array}{l} \frac{b_{1}}{(- 16) (- 5) - 8 \times 7} = \frac{b_{2}}{7 \times 3 - 3 (- 5)} = \frac{b_{3}}{3 \times 8 - 3 (- 16)} \\ \Rightarrow \frac{b_{1}}{24} = \frac{b_{2}}{36} = \frac{b_{3}}{72} \\ \Rightarrow \frac{b_{1}}{2} = \frac{b_{2}}{3} = \frac{b_{3}}{6} \end{array}$

Direction ratios of $\vec{b}$ are 2, 3, and 6.

$∴ \vec{b} = 2 \hat{i} + 3 \hat{j} + 6 \hat{k}$

Substituting $\vec{b} = 2 \hat{i} + 3 \hat{j} + 6 \hat{k}$ in equation (1), we obtain

$\vec{r} = (\hat{i} + 2 \hat{j} - 4 \hat{k}) + λ (2 \hat{i} + 3 \hat{j} + 6 \hat{k})$

This is the equation of the required line.

57. Prove that if a plane has the intercepts a,b,c and is at a distance of P units from the origin, then $\frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}} = \frac{1}{p^{2}}$

The equation of a plane having intercepts a, b, c with x, y, and z axes respectively is given by,

$\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1$

The distance (p) of the plane from the origin is given by,

$\begin{array}{l} p = | \frac{\frac{0}{a} + \frac{0}{b} + \frac{0}{c} - 1}{} | \\ \Rightarrow p = \frac{1}{} \\ \Rightarrow p^{2} = \frac{1}{\frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}}} \\ \Rightarrow \frac{1}{p^{2}} = \frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}} \end{array}$

Choose the correct answer in Exercise Q. 22 and 23.

58. Distance between the two planes: $2 x + 3 y + 4 z = 4 a n d 4 x + 6 y + 8 z = 12$ is

(A) 2 units (B) 4 units (C) 8 units (D) 2/√29 units

The equations of the planes are

$\begin{array}{l} 2 x + 3 y + 4 z = 4 & 4 x + 6 y + 8 z = 12 & \Rightarrow 2 x + 3 y + 4 z = 6 \end{array}$

It can be seen that the given planes are parallel.

It is known that the distance between two parallel planes, $a x + b y + c z = d_{1} a n d a x + b y + c z = d_{2},$ is given by,

$\begin{array}{l} D = | \frac{d_{2} - d_{1}}{} | \\ \Rightarrow D = | \frac{6 - 4}{} | \\ D = \frac{2}{} \end{array}$

Thus, the distance between the lines is 2/√29 units.

Hence, the correct answer is D.

59. The planes: $2 x - y + 4 z = 5 a n d 5 x - 2.5 y + 10 z = 6$ are

(A) Perpendicular (B) Parallel (C) intersect y-axis

(D) Passes through (0,0,5/4)

The equations of the planes are

$\begin{array}{l} 2 x - y + 4 z = 5 \dots (1) & 5 x - 2.5 y + 10 z = 6 \dots (2) \end{array}$

It can be seen that,

$\begin{array}{l} \frac{a_{1}}{a_{2}} = \frac{2}{5} \\ \frac{b_{1}}{b_{2}} = \frac{- 1}{- 2.5} = \frac{2}{5} \\ \frac{c_{1}}{c_{2}} = \frac{4}{10} = \frac{2}{5} \\ ∴ \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}} \end{array}$

Therefore, the given planes are parallel.

Hence, the correct answer is B.

If the lines $\frac{x - 3}{- 3} = \frac{y - 2}{2 k} = \frac{z - 3}{2} & \frac{x - 1}{3 k} = \frac{y - 1}{1} = \frac{z - 6}{- 5}$ are perpendicular, find the value of k

It is known that two lines with direction ratios, $a_{1}, b_{1}, c_{1} a n d a_{2}, b_{2}, c_{2}$ , are perpendicular, if $a_{1} a_{2} + b_{1} b_{2} + c_{1} c_{2} = 0$

$\begin{array}{l} ∴ - 3 (3 k) + 2 k \times 1 + 2 (- 5) = 0 \\ \Rightarrow - 9 k + 2 k - 10 = 0 \\ \Rightarrow 7 k = - 10 \\ \Rightarrow k = \frac{- 10}{7} \end{array}$

Therefore, for k= -10/7, the given lines are perpendicular to each other.

NCERT Class 12 Math Chapter 11 Three Dimensional Geometry Solutions- FAQs

Check a few of the most important FAQs of the chapter 3D Geometry below;

Maths Ncert Solutions class 12th Exam

Student Forum

Anything you would want to ask experts?

Write here...

Other Similar chapters for you

News & Updates

Latest NewsPopular News

Class 12 Maths Chapter 11 Three-Dimensional Geometry NCERT Solutions PDF Download

Understanding 3D Geometry in Class 12 – A Brief Insight

Class 12 Three Dimensional Geometry: Key Topics, Weightage

3D Geometry Class 12 Weightage in JEE Mains

Try these practice questions

Important Formulas of 3D Geometry Class 12

Class 12 Chapter 11 Three-Dimensional Geometry Important Formulae for CBSE and Competitive Exams

Download Class 12 Three-Dimensional Geometry NCERT Solution PDF for Free

More Useful Links

Class 12 Three Dimensional Geometry Exercise-wise Solutions

Class 12 Three Dimensional Geometry Exercise 11.1 Solutions

Commonly asked questions

NCERT Class 12 Math Chapter 11 Three Dimensional Geometry Solutions- FAQs

Student Forum

Other Similar chapters for you

News & Updates

UPPSC PCS Prelims Exam Analysis 2025 Live: Answer Key, Expected Cutoff

Bihar STET 2025 Admit Card (Download Link) OUT @biharstet.com LIVE: Download BSEB Hall Ticket

JAC Compartment Result 2025 Class 10, 12 (Anytime Soon) Live Updates: Check Jharkhand Board Matric, Inter Results Here

NIELIT DLC (CCC/CCCP/ECC/ACC/BCC) Examination Starts Today on Oct 12

SSC Stenographer 2025 Result (Link Soon) @ssc.gov.in Live: Download Result & Cutoff PDF Here

JEE Main Marks vs Percentile vs Rank 2025: Calculate Percentile and Rank Using Marks

List of NIT Colleges in India 2025 - NIRF Ranking, Courses, Seats, Cutoff, Fees and Placement

CBSE 10th Maths Question Paper 2025, 2024, 2023, 2022, 2020, 2019 PDF Download

NEET Chapter Wise Weightage 2026 PDF by NTA: Physics, Chemistry & Biology

List of Top IITs in India 2025: NIRF Ranking, Courses, Seats, Fees & Placement