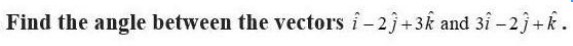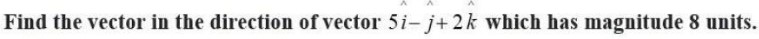Vector Algebra Class 12 covers the basic concepts of vectors, their algebraic and geometric properties, and various operations on vectors. Vector quantities include velocity, displacement, force, acceleration, momentum, weight, and electric field intensity. The chapter introduces the types of vectors, multiplication of a vector by a scalar, addition, and the product of vectors.
The subject matter experts at Shiksha created the Vectors Class 12 NCERT Solutions for students to deepen their concept clarity and score high in the CBSE Board and competitive exams like JEE Mains. This page also provides the Vector Algebra Class 12 PDF for students to download and prepare for the examination.
To get the topic-wise PDF and notes PDF for Class 12 Maths, check - Class 12 Maths Notes PDF for CBSE Exams.
- Glance at Vector Algebra Class 12
- Class 12 Math Chapter 10 Vector Algebra : Key Topics, Weightage
- Important Formulas of Class 12 Vector Algebra
- Class 12 Maths Vector Algebra NCERT Solutions PDF – Download for Free
- Class 12 Vector Algebra Exercise-wise NCERT Solutions
- Class 12 Vector Algebra Exercise 10.1 Solutions
Glance at Vector Algebra Class 12
Here is a quick review of Class 12 Maths Vector Algebra:
- The position vector of a point P(x, y, z) is given by and its magnitude by
- The scalar components of a vector represent its projections along the respective axes, and they are in direction ratios.
- The direction ratios (a, b, c), magnitude (r), and direction cosines (l,m,n) of any vector are related by -
- The chapter covers the vector sum of three sides of a triangle, two coinitial vectors, and the multiplication of vector.
To get access to the short revision notes of Chemistry, Physics, and Maths, check - NCERT Class 12 Notes.
Class 12 Math Chapter 10 Vector Algebra : Key Topics, Weightage
Before starting the preparation of any chapter, it is good to know the topics covered in it. See below the topics covered in the Vector Algebra Class 12:
| Exercise | Topics Covered |
|---|---|
| 10.1 | Introduction |
| 10.2 | Some Basic Concepts |
| 10.3 | Types of Vectors |
| 10.4 | Addition of Vectors |
| 10.5 | Multiplication of a Vector by a Scalar |
| 10.6 | Product of Two Vectors |
Vector Algebra Class 12 Weightage in JEE Main
| Exam | Number of Questions | Weightage |
|---|---|---|
| JEE Main | 2 questions | 8% |
Important Formulas of Class 12 Vector Algebra
Class 12 Math Chapter 10 Vector Algebra Important Formulae for CBSE and Competitive Exams
Students can check the important topics below;
Basic Vector Operations
- Position Vector: A point in 3D space has a position vector:
- Addition of Two Vectors: If and then:
- Magnitude of a Vector: For a vector
- Dot Product (Scalar Product): If and , then;
- Angle between Two Vectors:
- Cross Product (Vector Product): If and , then;
- Magnitude of Cross Product:
- Projection of a Vector:
-
Projection of on :
-
Vector Component of along :
- Collinearity of Two Vectors: Two vectors and are collinear if;
- Vector Equation of a Line
-
Vector form: A line passing through and parallel to :
-
Cartesian form: A line passing through and parallel to :
Class 12 Maths Vector Algebra NCERT Solutions PDF – Download for Free
Students should download the Vector Algebra Class 12 PDF from the link given below. The solutions are given in a step-by-step format. It is easy to understand and improves the problem-solving skills of students.
Class 12 Math Chapter 10 Vector Solution PDF: Free PDF Download
Related Links
| NCERT Notes for Class 11 & 12 | Class 12 Maths NCERT Solutions | NCERT Solutions Class 11 and 12 |
Class 12 Vector Algebra Exercise-wise NCERT Solutions
This chapter introduces concepts like vector operations, dot and cross products, scalar triple products, and their real-world significance. Mastering these topics is crucial for excelling in board exams and competitive entrance tests.
Class 12 Vector Algebra Exercise 10.1 Solutions
Class 12 Vector Algebra Exercise 10.1 Solutions
Class 12 Vector Algebra Exercise 10.1 deals with key concepts such as vectors, their representation, operations like addition, subtraction, and scalar multiplication, as well as their geometric interpretations. Shiksha has provided detailed solutions to all the problems in Vector Algebra Exercise 10.1, ensuring that students grasp the concepts thoroughly. Vector Algebra Class 12 Exercise 10.1 Solutions consists of 5 Questions. Students can check the complete solution for VEctor Algebra Exercise 10.1 below;
Class 12 Vector Algebra Exercise 10.1 Solutions
| Q1. Represent graphically a displacement of 40 km, 30° east of north. |
| A.1. east of north. |
|
(i) 10 kg (ii) 2 meters north-west (iii) 40° (iv) 40 Watt (v) 10–19 coulomb (vi) 20 m/sec2 |
| A.2. (i) 10kg involves only magnitude. So, it is scalar quantity. (ii) 2 meters north-west involves both magnitude and direction. So, it is vector quantity. (iii) 400 involves only magnitude. So, it is scalar quantity. (iv) 400 watts involves only magnitude. So, it is scalar quantity. (v) 10-19 coulomb involves only magnitude. So, it is scalar quantity. (vi) 20m/s-2 involves magnitude and direction. So, it is vector quantity. |
| Q3. Classify the following as scalar and vector quantities: (i) time period (ii) distance (iii) force (iv) velocity (v) work done |
| A.3. (i) Time period involves only magnitude. So, it is scalar quantity. (ii) Distance involves only magnitude. So, it is scalar quantity. (iii) Force involves both magnitude and direction. So, it is vector quantity. (iv) Velocity involves both magnitude and direction. So, it is vector quantity. (v) Work done involves only magnitude. So, it is scalar quantity. |
| Q..4. In the adjoining figure, (a square) identify the following vectors: (ii) Equal (iii) Collinear but not equal. |
| A.4. (a) Vector and are co initial same initial point. (b) and same magnitude & direction. (c) and are collinear but not equal they are parallels their direction are not same. |
Commonly asked questions
25. Kindly Consider the following
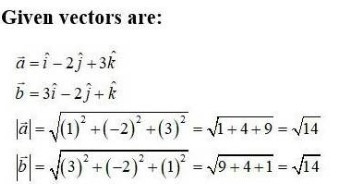
Now,
Also, we know,

49. If either = 0 and = 0 then Is the converse true? Justify your answer with an example.
We take any parallel non- zero vectors so that .

13. For given vectors , find the unit vector in the direction of
Given,
The sum of given vectors is given by
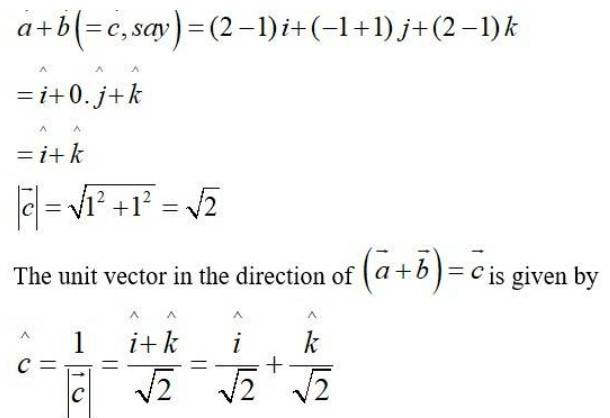
14. Kindly Consider the following
Kindly go through the solution
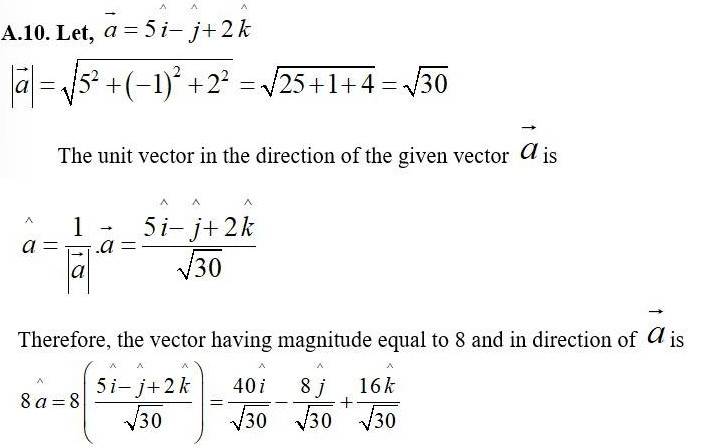
19. Find the position vector of a point R which divides the line joining two points P and Q. whose position vectors are and - respectively, in the ratio 2 : 1
(i) Internally
(ii) Externally
(i) The position vector of point R dividing the join of P and Q. internally in
the ratio 2:1 is,
(ii) The position vector of the point k dividing the join of P and Q. externally in the ratio 2:1
A15. (ii)
65. Let Find a vector which is perpendicular to both and and = 15
Given,
Let,
Since, is perpendicular to both
We know,
Putting this value in (3) we get
Putting value in (2), we get
The reQ.uired vector is
29. Find and ,if and
and ,if and
23. If and are two collinear vectors, then which of the following are incorrect:
(A) = λ for some scalar λ
(B) = ±
(C) The respective components of and are proportional.
(D) Both the vectors and have same direction, but different magnitudes.
We know,
If and are two collinear vector, they are parallel.
So,
Hence, the respective component are proportional but, vector and can have different direction.
Thus, the statement given in D is incorrect.
The correct answer is D.
3. Classify the following as scalar and vector quantities:
(i) Time period
(ii) Distance
(iii) Force
(iv) Velocity
(v) Work done
(i) Time period involves only magnitude. So, it is scalar quantity.
(ii) Distance involves only magnitude. So, it is scalar quantity.
(iii) Force involves both magnitude and direction. So, it is vector quantity.
(iv) Velocity involves both magnitude and direction. So, it is vector quantity.
(v) Work done involves only magnitude. So, it is scalar quantity.
47. Given that and What can you conclude about the vectors and ?
Given,
and
For,
, then either or or
For,
, then either or or
In case and are non- zero on both side.
But and cannot be both perpendicular and parallel simultaneously.
So, we can conclude that
or
48. Let the vectors be given as then show that
Given,
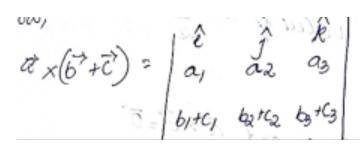
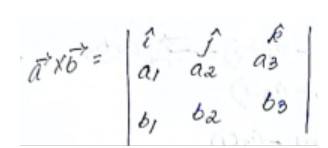
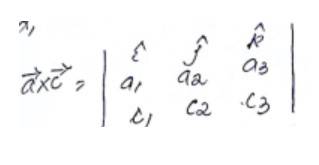
Adding (2) and (3), we get
From (1) and (4), we have
Hence, proved.
12. Find the unit vector in the direction of the vector where P and Q. are the points (1, 2, 3) and (4, 5, 6) respectively.
Given,
So,
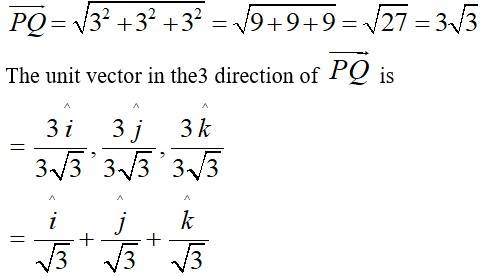
17. Find the direction cosines of the vector joining the points A (1, 2, –3) and B (–1, –2, 1) directed from A to B.
Given, A(1,2,-3) and (-1,-2,1)
Now,
Then,
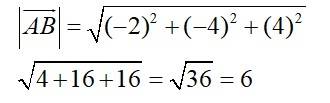
Let, l, m, n be direction cosine,
Therefore, direction cosine of are
7. Write two different vectors having same magnitude.
Two different vectors having same magnitude: -
(i)
(ii)
15. Show that the vectors are collinear.
Let,
It is seen that
Where,
Therefore, we can say that the given vector are collinear.
16. Find the direction cosines of the vector
Let

53. Area of a rectangle having vertices A, B, C and D with position vectors respectively is:
(A)
(B) 1
(C) 2
(D) 4
(c) Given,
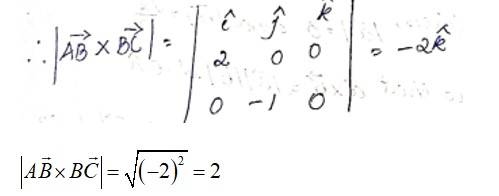
66. The scalar product of the vector with a unit vector along the sum of vectors is equal to one. Find the value of λ.
The unit vector along is given as;
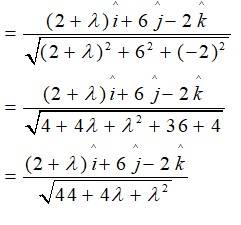
By Q.uestion, scalar product of with this unit vector is 1.
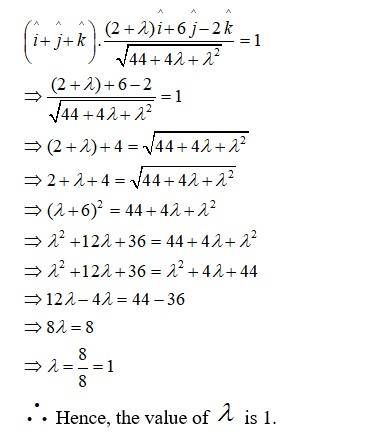
67. If are mutually perpendicular vectors of equal magnitudes, show that the vector -is equally inclined to and .
Given that are mutually perpendicular vectors, we have
Let, vector be inclined to at angles, respectively.
Therefore, the vector are equally inclined to
9. Find the scalar and vector components of the vector with initial point (2, 1) and terminal point (–5, 7).
Let the vector with initial point P (2,1) and terminal point Q. (-5,7) can be shown as,
The scalar components are -7 and 6.
The vector components are -7i and 6j.
18. Show that the vector is equally inclined to the axes OX, OY and OZ.
Here,
Let,
Then,
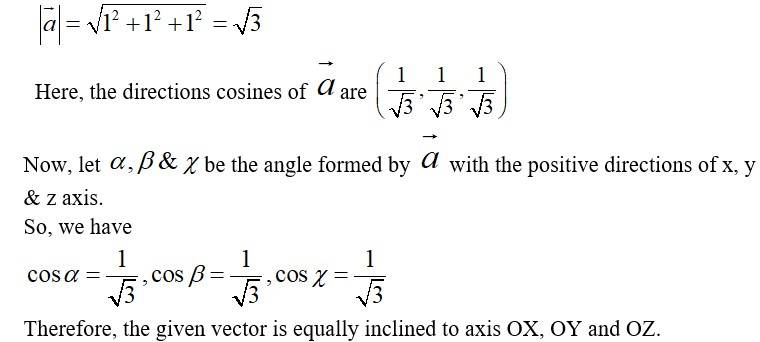
8. Find the values of x and y so that the vectors are equal.
Note that two vector are equal only if their corresponding components are equal.
Thus, the given vectors and will be equal if and only if
20. Find the position vector of the mid-point of the vector joining the points P (2, 3, 4) and Q. (4, 1, – 2).
The Position vector of mid-point R of the vector joining point P (2,3,4) and Q (4,1, -2) is given by;
24. Find the angle between two vectors and with magnitude √3 and 2 respectively having . = √6
Given,
=√3
We have,
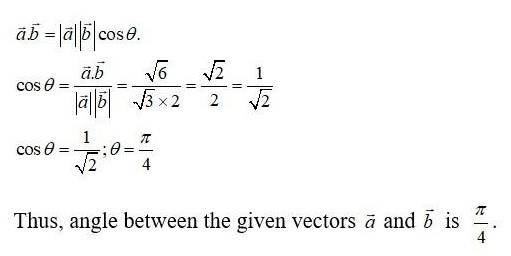
32. Find if for a unit vector .
36. If and are unit vectors such that = 0 find the value of
40. Show that the vectors form the vertices of a right angled triangle.
Let vector and be position vector of point A, B, C respectively.
So,
Now, vectors and represents the sides of .
Hence,
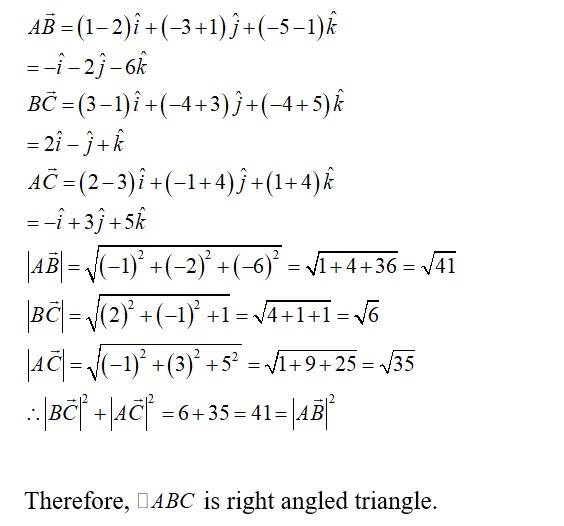
70. Choose the correct answer:
Let and be two unit vectors andθ is the angle between them. Then is a unit vector if
(A) θ =
(B) θ =
(C) θ =
(D) θ =
Let, be two unit vectors and be the angle between them.
Then,
Now, is a unit vector if
[ is unit vector.]
Therefore, the correct answer is (D)
50. Find the area of the triangle with vertices A (1, 1, 2), B (2, 3, 5) and C (1, 5, 5).
Given,
We have,
The area of given triangle is


Given,
The area of a parallelogram with and as its adjacent sides is given by
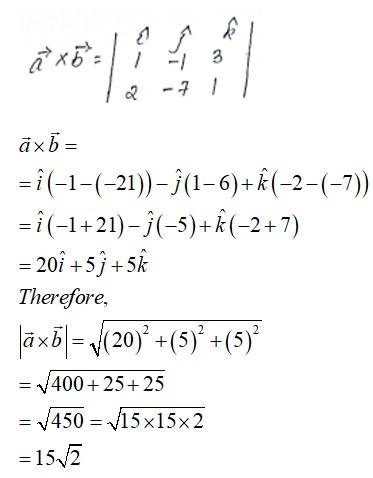
52. Let the vectors and such that | | = 3 and | | = √2/3 then is a unit vector, if the angle between and is:
(A)
(B)
(C)
(D)
(B) Given,

Hence, is a unit vector if angle between and is
54. Write down a unit vector in XY-plane making an angle of 30° with the positive direction of x-axis.
Let be unit vector in the XY-plane then,
is the angle made by the unit vector with the positive direction of the X-axis.
Then,

ReQ.uired unit vector
55. Find the scalar components and magnitude of the vector joining the points
Given,
Point
= Position vector of Q.- Position vector of P
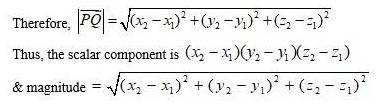
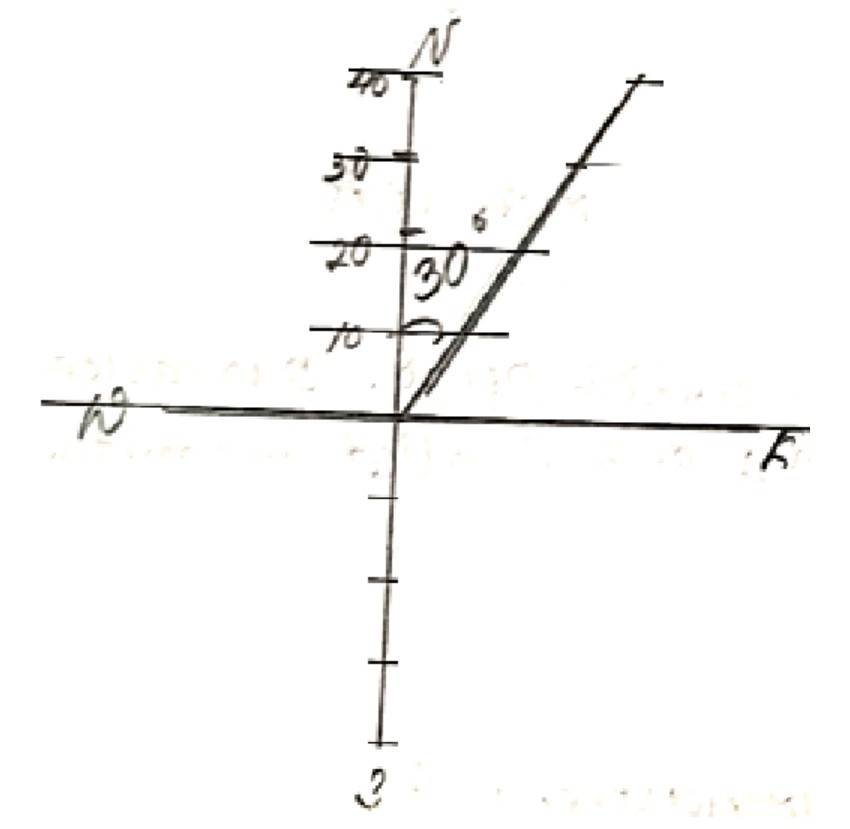
56. A girl 4 Km towards west, then she walks 3 Km in a direction 30° east of north and stops. Determine the girls displacement from her initial point of departure.

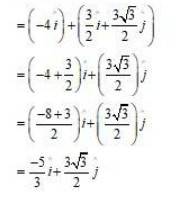
The girl’s displacement from her initial point of departure is
57. If then is it true that Justify your answer.
Let us take a , which
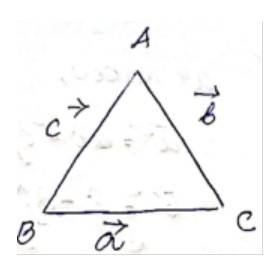
So, by triangle law of vector addition, we have
And, we know that represent, the sides of
Also, it is known that the sum of the length of any slides of a triangle is greater than the third side.
Hence, it is not true that
58. Find the value of x for which is a unit vector.
Given,
is a unit vector.
So,
Now,
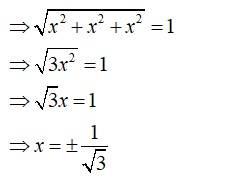

59. Find a vector of magnitude 5 units and parallel to the resultant of the vectors
We know,
Let, be the resultant of and
Then,

60. If find a unit vector parallel to the vector
Given,
Then,
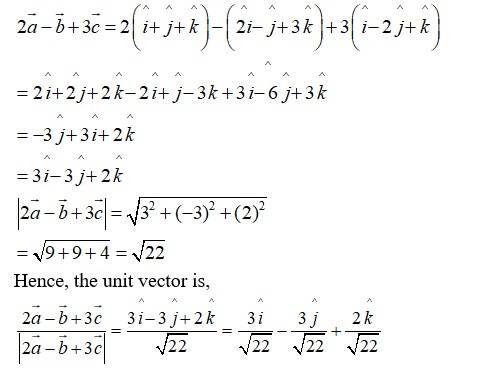
61. Show that the points A (1, –2, –8), B (5, 0, –2) and C (11, 3, 7) are collinear and find the ratio in which B divides AC.
Given,
Now,

Thus, A,B and C are collinear.
Let, be the ratio that point B divides AC.
We have,
On eQ.uating the corresponding component , we get
Hence, point B divides AC in the ratio
62. Find the position vector of a point R which divides the line joining the two points P and Q whose position vectors are and externally in the ratio 1 : 2. Also, show that P is the middle point of line segment RQ.
Given,
It is given that point R divides a line segment joining two points P and Q.
externally in the ratio 1:2 Then,
Position vector of the mid-point of RQ.
63. Two adjacent sides of a parallelogram are . Find the unit vector parallel to its diagonal. Also, find its area.
Given,
Adjacent sides of parallelogram are
Diagonal of parallelogram =
Thus, the unit vector parallel to diagonal
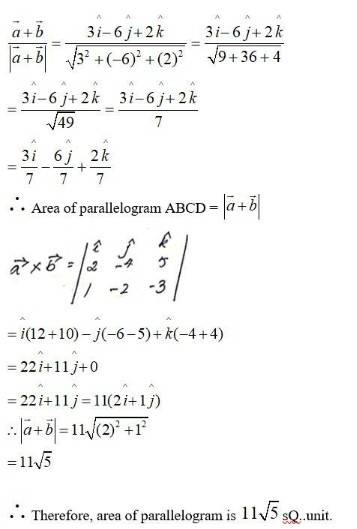
64. Show that the direction cosines of a vector equally inclined to the axes OX,Oy and OZ 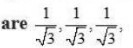
Kindly go through the solution
68. Prove that if and only if are perpendicular given .
( Distributive of scalar product over addition )
( Scalar product is commutative , )
Therefore, are perpendicular.
69. Choose the correct answer:
If θ is the angle between two vectors and then only when:
(A)
(B)
(C)
(D)
Let, in triangle between two vector
Then, without loss of generality, are non-zero vector so that
are positive.
We know,
So,
Therefore, , when
Hence, the correct answer is B.
10. Find the sum of the vectors:
The given vectors are
The sum of the vector is
21. Show that the points A, B and C with position vectors respectively form the vertices of a right angled triangle.
We have,
Now,
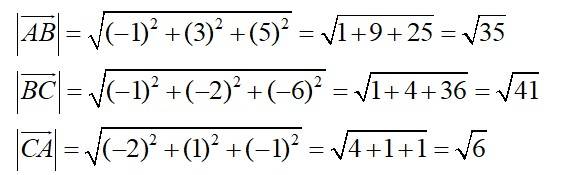
Hence,
Hence, given points from the vertices of a right angled triangle.
11. Find the unit vector in the direction of the vector
Kindly go through the solution
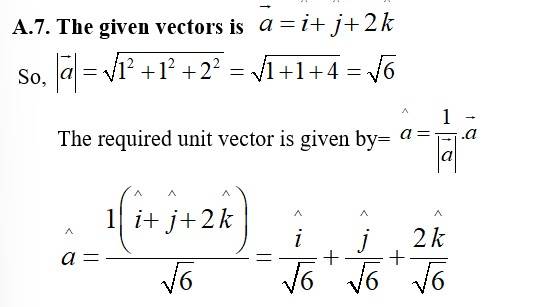
22. In triangle ABC (Fig. below), which of the following is not true:
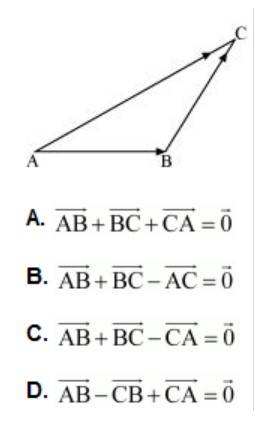
(A)
By triangle law of addition in given triangle, we get:
So, (A) is true.
(B)
So, (B) is true.
(C)
The eQ.uation in alternative C , which is not true, is incorrect.
(D)
The, equation given is alternative is D is true.
The correct answer is C.
26. Find the projection of the vector
on the vector
Let,
The projection of vector on is given by,
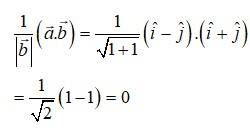
The projection of vector on is 0.
27. Find the projection of the vector on the vector
Let,
The project of vector on is.
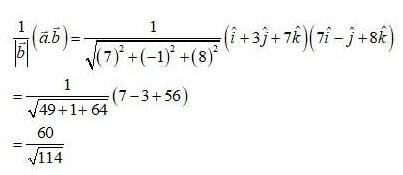
28. Kindly Consider the following
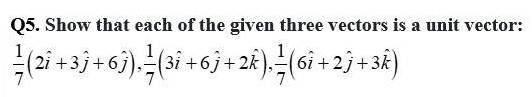
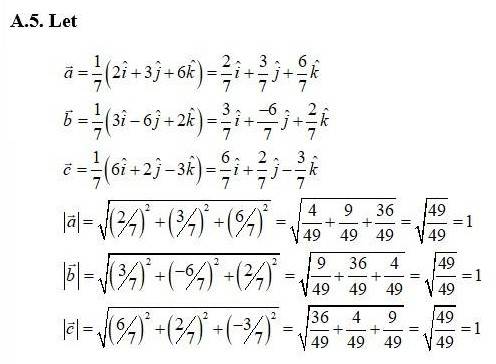
Here, each of the given three vector is a unit vector.
Therefore, the given three vectors are mutually perpendicular to each other.
30. Evaluate the product
31. Find the magnitude of two vectors and having the same magnitude such that the angle between them is 60° and their scalar product is 1/2.
Let be the angle between the vectors and .
It is given that
We know,
Magnitude of two vector=1
33. If are such that is perpendicular to then find the value of λ
Given,
Now,
If is perpendicular to , then
Therefore, the required value of is 8.
34. Show that is perpendicular to for any two non-zero vectors and
Therefore, and are perpendicular.
35. If and . = 0 and . = 0 , then what can be concluded about the vector ?
We know,
and
Now,
is a zero vector.
Thus, vector satisfying can be any vector.
37. If either vector . But the converse need not be true. Justify your answer with an example.
Consider
and
Then,
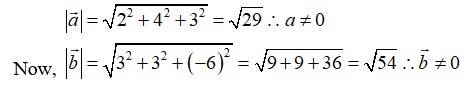
Therefore, the converse of the given statement need not be true.
38. If the vertices A, B, C of a triangle ABC are (1, 2, 3), (–1, 0, 0), (0, 1, 2), respectively, then find ∠ABC. [∠ABC is the angle between the vectors and ]
Vertices of are given as
is the angle between the vectors and
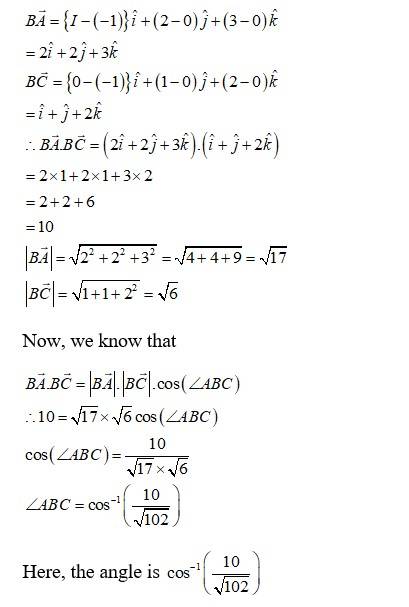
39. Show that the points A (1, 2, 7), B (2, 6, 3) and C (3, 10, –1) are collinear.
Given, point are
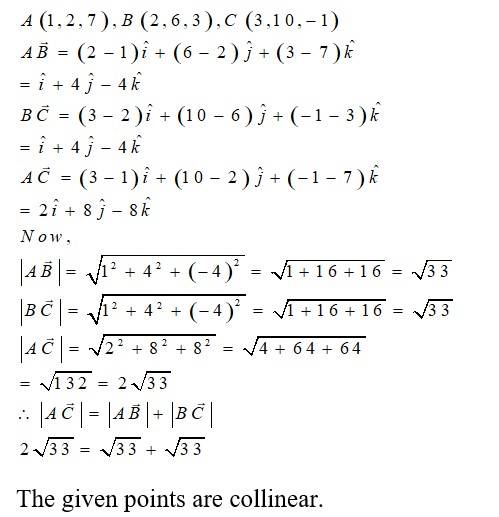
41. If is a nonzero vector of magnitude ‘a’ and λ a nonzero scalar, then λ is unit vector if
(A) λ = 1
(B) λ = –1
(C) a = | λ
|(D) a = 1/|λ|
Vector is a unit vector if
Now,
Therefore, vectar is a unit vector if a= .
Option (D)is correct.
42. Find if and
Kindly go through the solution
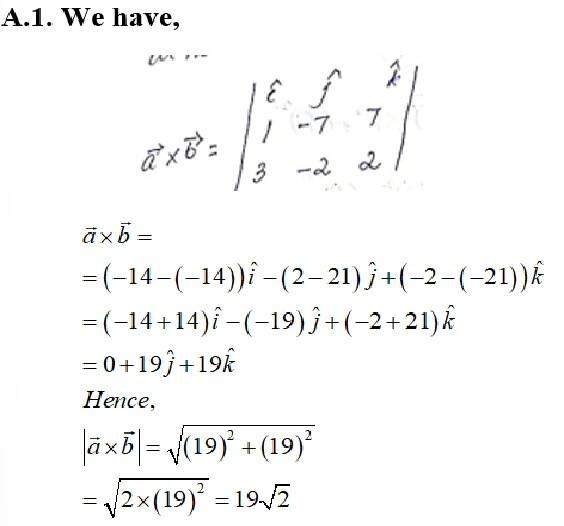
43. Find a unit vector perpendicular to each of the vectors
Given,
A vector which is perpendicular to both and is given by
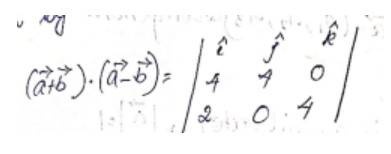
Say
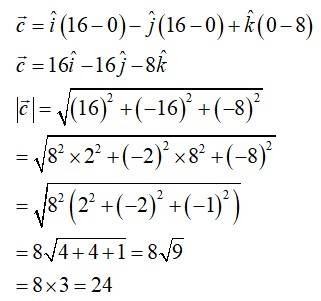
Therefore, the unit vector is
71. Choose the correct answer:
The value of is:
(A) 0
(B) -1
(C) 1
(D) 3
Therefore, the correct answer is (C)
72. If θ be the angle between any two vectors and , then when θ is equal to:
(A) 0
(B)
(C)
(D) π
Let, be angle between two vector . Then, without loss of generality, are non-zero vectors, so that are positive. Therefore, the correct answer is B. |
1. Represent graphically a displacement of 40 km, 30° east of north.
east of north.
(i) 10 kg
(ii) 2 meters north-west
(iii) 40°
(iv) 40 Watt
(v) 10–19 coulomb
(vi) 20 m/sec2
(i) 10kg involves only magnitude. So, it is scalar quantity.
(ii) 2 meters north-west involves both magnitude and direction. So, it is vector quantity.
(iii) 400 involves only magnitude. So, it is scalar quantity.
(iv) 400 watts involves only magnitude. So, it is scalar quantity.
(v) 10-19 coulomb involves only magnitude. So, it is scalar quantity.
(vi) 20m/s-2 involves magnitude and direction. So, it is vector quantity.
4. In the adjoining figure, (a square) identify the following vectors:
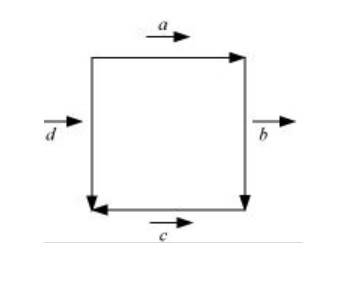
(ii) Equal
(iii) Collinear but not equal.

(a) Vector and are co initial same initial point.
(b) and same magnitude & direction.
(c) and are collinear but not equal they are parallels their direction are not same.
5. Answer the following as true or false:
(i) and - are collinear.
(ii) Two collinear vectors are always equal in magnitude.
(iii) Two vectors having same magnitude are collinear.
(iv) Two collinear vectors having the same magnitude are equal.
(i) True, as vector quantity and - are parallel to same line.
(ii) False, as collinear vector are those vectors that are parallel to same line, but it is not necessary that they are equal also.
(iii) False, as two vectors having same magnitude may have different directions, so they are not collinear.
(iv) False, as two collinear vectors having same magnitude are not equal whey they are opposite in direction.
7. Compute the magnitude of the following vectors:
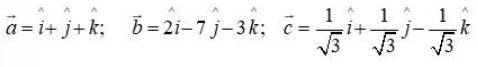
Kindly go through the solution
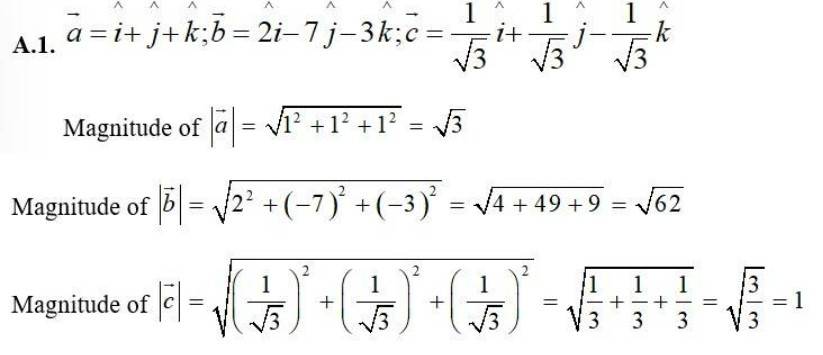
44. If a unit vector makes an angle π/3 with and an acute angle θ with then find θ and hence, the components of .
Let as component
We know,
is a unit vector,
Given that,
marks angles with , with and with acute angle.
Now,
We know,

45. Show that
Show that
46. Find λ and μ if

On comparing both side components,
Therefore, the value of and
Maths Ncert Solutions class 12th Exam