If p is a real number and if the middle term in the expansion of (p2 +2)8 is 1120, find p .

This is a Long Answer Type Questions as classified in NCERT Exemplar Sol: Given expression is (P2+2)8 N u m b e r o f t e r m s = 8 + 1 = 9 ( o d d ) ∴ M i d d l e t e r m ( n + 1 2 ) t h t e r m = 9 + 1 2 = 1 0 2 = 5 t h t e r m T 5 = T 4 + 1 = C 4 8 ( P 2 ) 8 − 4 ( 2 ) 4 = C 4 8 P 4 2 4 × 2 4 = C 4 8 P 4 N o w C 4 8 P 4 = 1 1 2 0 ⇒ 8 × 7 × 6 × 5 4 × 3 × 2 × 1 . P 4 = 1 1 2 0 ⇒ 7 0 P 4 = 1 1 2 0 ⇒ P 4 = 1 1 2 0 7 0 = 1 6 ⇒ P 4 = 2 4 ⇒ P = ± 2 H e n c e , t h e r e q u i r e d v a l u e o f P = ± 2 .

If xp occurs in the expansion of (x2+1x)2n, prove that its coefficient is 4n-p32n+p3.

This is a Long Answer Type Questions as classified in NCERT Exemplar Sol: The given expression is (x2+1x)2n G e n e r a l T e r m T r + 1 = C r n x n − r y r = C r 2 n ( x 2 ) 2 n − r ( 1 x ) r = C r 2 n ( x ) 4 n − 2 r . 1 x r = C r 2 n ( x ) 4 n − 2 r − r = C r 2 n ( x ) 4 n − 3 r I f x p o c c u r s i n ( x 2 + 1 x ) 2 n t h e n 4 n − 3 r = p ⇒ 3 r = 4 n − p ⇒ r = 4 n − p 3 ∴ C o e f f i c i e n t o f x p = C r 2 n = C 4 n − p 3 2 n = ( 2 n ) ! ( 4 n − p 3 ) ! ( 2 n − 4 n − p 3 ) ! = ( 2 n ) ! ( 4 n − p 3 ) ! ( 6 n − 4 n + p 3 ) ! = ( 2 n ) ! ( 4 n − p 3 ) ! ( 2 n + p 3 ) ! H e n c e , c o e f f i c i e n t o f x p = ( 2 n ) ! ( 4 n − p 3 ) ! ( 2 n + p 3 ) !

Find the term independent of x , x ≠ 0 , in the expansion of (3x2/2 – 1/3x)15

This is a Short Answer Type Questions as classified in NCERT Exemplar Sol: G e n e r a l T e r m T r + 1 = C r n x n − r y r = C r 1 5 ( 3 x 2 2 ) 1 5 − r ( − 1 3 x ) r = C r 1 5 ( 3 2 ) 1 5 − r ( x ) 3 0 − 2 r ( − 1 3 ) r 1 x r = C r 1 5 ( 3 2 ) 1 5 − r ( x ) 3 0 − 2 r − r ( − 1 ) r 1 ( 3 ) r = C r 1 5 ( 3 2 ) 1 5 − r ( x ) 3 0 − 3 r ( − 1 ) r 1 ( 3 ) r f o r g e t t i n g t h e t e r m i n d e p e n d e n t o f x , 3 0 − 3 r = 0 ⇒ r = 1 0 On putting the value of r in the above expression, we get = C 1 0 1 5 ( 3 2 ) 1 5 − 1 0 ( − 1 ) 1 0 1 ( 3 ) 1 0 = C 1 0 1 5 ( 3 ) 5 ( 2 ) 5 . 1 ( 3 ) 1 0 = C 1 0 1 5 . 1 ( 2 ) 5 . ( 3 ) 5 = C 1 0 1 5 ( 1 6 ) 5 H e n c e , t h e r e q u i r e d t e r m = C 1 0 1 5 ( 1 6 ) 5

If the term free from x in the expansion of x – k/x2 10 is 405, find the value of k .

This is a Short Answer Type Questions as classified in NCERT Exemplar Sol: The given expression is (x−Kx2)10 G e n e r a l T e r m T r + 1 = C r n x n − r y r = C r 1 0 ( x ) 1 0 − r ( − K x 2 ) r = C r 1 0 ( x ) 1 0 − r 2 ( − K ) r ( 1 x 2 r ) = C r 1 0 ( x ) 1 0 − r 2 − 2 r ( − K ) r = C r 1 0 ( x ) 1 0 − r − 4 r 2 ( − K ) r = C r 1 0 ( x ) 1 0 − 5 r 2 ( − K ) r f o r g e t t i n g t h e t e r m i n d e p e n d e n t o f x , 1 0 − 5 r 2 = 0 ⇒ r = 2 On putting the value of r in the above expression, we get = C 2 1 0 ( − K ) 2 A c c o r d i n g t o t h e c o n d i t i o n o f t h e q u e s t i o n , w e h a v e C 2 1 0 K 2 = 4 0 5 ⇒ 1 0 . 9 2 . 1 K 2 = 4 0 5 ⇒ 4 5 K 2 = 4 0 5 ⇒ K 2 = 4 0 5 4 5 = 9 ∴ K = ± 3 H e n c e , t h e v a l u e o f K = ± 3

Find the middle term(s) in the expansion of: (x/a−ax)10. 3x – x3/6 9

This is a Short Answer Type Questions as classified in NCERT Exemplar Sol: (i)Given expression is (xa−ax)10 N u m b e r o f t e r m s = 1 0 + 1 = 1 1 ( o d d ) ∴ M i d d l e t e r m ( n + 1 2 ) t h t e r m = 1 1 + 1 2 = 1 2 2 = 6 t h t e r m G e n e r a l t e r m T r + 1 = C r n x n − r y r ⇒ T 5 + 1 = C 5 1 0 ( x a ) 1 0 − 5 ( − a x ) 5 = − C 5 1 0 x 5 a 5 . a 5 x 5 = − C 5 1 0 = − 1 0 × 9 × 8 × 7 × 6 5 × 4 × 3 × 2 × 1 . = − 9 × 7 × 4 = − 2 5 2 H e n c e , t h e r e q u i r e d m i d d l e t e r m = − 2 5 2 (ii)Given expression is (3x−x36)9 N u m b e r o f t e r m s = 9 + 1 = 1 0 ( e v e n ) ∴ M i d d l e t e r m s a r e ( n 2 ) t h t e r m a n d ( n 2 + 1 ) t h t e r m ( 1 0 2 ) t h = 5 t h t e r m a n d ( 1 0 2 + 1 ) t h = 6 t h t e r m G e n e r a l t e r m T r + 1 = C r n x n − r y r ∴ T 5 = T 4 + 1 = C 4 9 ( 3 x ) 9 − 4 ( − x 3 6 ) 4 = C 4 9 ( 3 ) 5 . x 5 ( − 1 6 ) 4 . x 1 2 = 9 × 8 × 7 × 6 4 × 3 × 2 × 1 × 3 × 3 × 3 × 3 × 3 6 × 6 × 6 × 6 x 1 7 = 1 8 9 8 x 1 7 N o w , T 6 = T 5 + 1 = C 5 9 ( 3 x ) 9 − 5 ( − x 3 6 ) 5 = C 5 9 ( 3 ) 4 . x 4 ( − 1 6 ) 5 . x 1 5 = 9 × 8 × 7 × 6 × 5 5 × 4 × 3 × 2 × 1 ( 3 ) 4 ( − 1 6 ) 5 . x 1 9 = − 2 1 1 6 x 1 9 H e n c e , t h e r e q u i r e d m i d d l e t e r m s a r e 1 8 9 8 x 1 7 a n d − 2 1 1 6 x 1 9

The sum of the series 10 20 r =0 Cr is 219 + 20 C10/2

This is a True or False Type Questions as classified in NCERT Exemplar Sol: ∑ r = 0 1 0 C r 2 0 = C 0 2 0 + C 1 2 0 + C 2 2 0 + C 3 2 0 + … + C 1 0 2 0 = C 0 2 0 + C 1 2 0 + … + C 1 0 2 0 + C 1 1 2 0 + … + C 2 0 2 0 − ( C 1 1 2 0 + … + C 2 0 2 0 ) = 2 2 0 − ( C 1 1 2 0 + … + C 2 0 2 0 ) H e n c e , t h e g i v e n s t a t e m e n t i s ' F a l s e '

In the expansion of x2 – 1/x2 16 , the value of the constant term is ________________ .

This is a Fill in the Blanks Type Questions as classified in NCERT Exemplar Sol: Let Tr+1 be the constant term in the expansion of (x2−1x2)16 ∴ T r + 1 = C r 1 6 ( x 2 ) 1 6 − r ( − 1 x 2 ) r = C r 1 6 ( x ) 3 2 − 2 r ( − 1 ) r . 1 x 2 r = ( − 1 ) r . C r 1 6 ( x ) 3 2 − 2 r − 2 r = ( − 1 ) r . C r 1 6 ( x ) 3 2 − 4 r F o r g e t t i n g c o n s t a n t t e r m , 3 2 − 4 r = 0 ⇒ r = 8 ∴ T r + 1 = ( − 1 ) 8 . C 8 1 6 = C 8 1 6 H e n c e , t h e v a l u e o f t h e f i l l e r i s C 8 1 6 .

If the seventh terms from the beginning and the end in the expansion of are equal, then n equals _________________ . [Hint: T7=Tn−7+2 , = nC6 (2 /3)n-6 (1/3 1/3 6) = nCn – 6 (2 1/3 6 (1/3 1/3) n - 6 solve for n. ] = (2 1/3)n – 12 = 1/3 1/3 n -12 = only problem when n – 12 = 0 = n =12].

This is a Fill in the Blanks Type Questions as classified in NCERT Exemplar Sol: The given expansion is (+1)n ∴ T 7 = T 6 + 1 = C 6 n ( 2 1 / 3 ) n − 6 . 1 ( 3 1 / 3 ) 6 = C 6 n ( 2 ) n − 6 3 ( − 1 ) r . 1 ( 3 ) 2 N o w t h e T 7 f r o m t h e e n d = T 7 f r o m t h e b e g i n n i n g i n ( 1 + ) n . ∴ T 7 = T 6 + 1 = C 6 n ( 1 3 1 / 3 ) n − 6 . ( 2 1 / 3 ) 6 A s p e r t h e q u e s t i o n s , w e g e t C 6 n ( 2 ) n − 6 3 . ( 1 3 2 ) = C 6 n . 1 3 n − 6 3 . ( 2 ) 2 ⇒ ( 2 ) n − 6 3 . ( 3 ) − 2 = ( 3 ) − ( n − 6 3 ) . ( 2 ) 2 ⇒ ( 2 ) n − 6 3 − 2 . ( 3 ) − 2 + n − 6 3 = 1 ⇒ ( 2 ) n − 1 2 3 . ( 3 ) n − 1 2 3 = 1 ⇒ ( 6 ) n − 1 2 3 = ( 6 ) 0 ⇒ n − 1 2 3 = 0 ⇒ n = 1 2 H e n c e , t h e v a l u e o f t h e f i l l e r i s 1 2 .

The coefficient of a−6b4 in the expansion of (1a+2b3)10 is _________________ . [Hint: T5 = 10C4 1/a b -2b/3 4 = 1120/27 a-6b4]

This is a Fill in the Blanks Type Questions as classified in NCERT Exemplar Sol: The given expansion is (1a−2b3)10 F r o m a − 6 b 4 , w e c a n t a k e r = 4 ∴ T 5 = T 4 + 1 = C 4 1 0 ( 1 a ) 1 0 − 4 . ( − 2 b 3 ) 4 = C 4 1 0 ( 1 a ) 6 . ( − 2 3 ) 4 . b 4 = 1 0 . 9 . 8 . 7 4 . 3 . 2 . 1 × 1 6 8 1 . a − 6 b 4 = 2 1 0 × 1 6 8 1 . a − 6 b 4 = 1 1 2 0 2 7 . a − 6 b 4 H e n c e , t h e v a l u e o f t h e f i l l e r i s 1 1 2 0 2 7 .

Maths NCERT Exemplar Solutions Class 11th Chapter Eight: Overview, Questions, Preparation

Updated on Jul 23, 2025 15:30 IST

By Vishal Baghel, Executive Content Operations

CCCCC

Table of contents

Binomial Theorem Long Answer Type Questions
Binomial Theorem Short Answer Type Questions
Binomial Theorem Objective Type Questions
Binomial Theorem Fill in the Blanks
Binomial Theorem True or False Type Questions
JEE Mains

Binomial Theorem Long Answer Type Questions

If $p$ is a real number and if the middle term in the expansion of ${(\frac{p}{2} + 2)}^{8}$ is 1120, find $p$ .

\begin{array}{l} G i v e n expression i s {(\frac{P}{2} + 2)}^{8} \\ N u m b e r o f t e r m s = 8 + 1 = 9 (o d d) \\ ∴ M i d d l e t e r m {(\frac{n + 1}{2})}^{t h} t e r m = \frac{9 + 1}{2} = \frac{10}{2} = 5^{t h} t e r m \\ T_{5} = T_{4 + 1} = {}_{8}{C_{4}} {(\frac{P}{2})}^{8 - 4} {(2)}^{4} \\ = {}_{8}{C_{4}} \frac{P^{4}}{2^{4}} \times 2^{4} = {}_{8}{C_{4}} P^{4} \\ N o w {}_{8}{C_{4}} P^{4} = 1120 \Rightarrow \frac{8 \times 7 \times 6 \times 5}{4 \times 3 \times 2 \times 1} . P^{4} = 1120 \\ \Rightarrow 70 P^{4} = 1120 \Rightarrow P^{4} = \frac{1120}{70} = 16 \\ \Rightarrow P^{4} = 2^{4} \Rightarrow P = \pm 2 \\ H e n c e, t h e r e q u i r e d v a l u e o f P = \pm 2 . \end{array}

Show that the middle term in the expansion of (x – 1/x)2n is 1 × 3 × 5 × … (2n -1)/n × (-2)n.

\begin{array}{l} G i v e n expression i s {(x - \frac{1}{x})}^{2 n} \\ N u m b e r o f t e r m s = 2 n + 1 = 9 (o d d) \\ ∴ M i d d l e t e r m {(\frac{n + 1}{2})}^{t h} t e r m = \frac{2 n + 1 + 1}{2} = (n + 1) t h t e r m . \\ G e n e r a l T e r m T_{r + 1} = {}_{n}{C_{r}} x^{n - r} y^{r} \\ ∴ T_{n + 1} = {}_{2 n}{C_{n}} {(x)}^{2 n - n} {(- \frac{1}{x})}^{n} = {}_{2 n}{C_{n}} {(x)}^{n} {(- 1)}^{n} . \frac{1}{x^{n}} \\ = {(- 1)}^{n} . {}_{2 n}{C_{n}} = {(- 1)}^{n} . \frac{2 n!}{n! (2 n - n)!} \\ = {(- 1)}^{n} . \frac{2 n!}{n! n!} = {(- 1)}^{n} . \frac{2 n (2 n - 1) (2 n - 2) (2 n - 3) \dots 1}{n! n (n - 1) (n - 2) (n - 3) \dots 1} \\ = {(- 1)}^{n} . \frac{2 n (2 n - 1) . 2 (n - 1) (2 n - 3) \dots 1}{n! n (n - 1) (n - 2) (n - 3) \dots 1} \\ = \frac{{(- 1)}^{n} . 2^{n} . [n (n - 1) (n - 1) \dots] . [(2 n - 1) . (2 n - 3) \dots 5.3.1]}{n! . n (n - 1) (n - 2) \dots 1} \\ = \frac{{(- 2)}^{n} [(2 n - 1) . (2 n - 3) \dots 5.3.1]}{n!} \\ = \frac{1 \times 3 \times 5 \times \dots (2 n - 1)}{n!} \times {(- 2)}^{n} \\ H e n c e, t h e m i d d l e t e r m = \frac{1 \times 3 \times 5 \times \dots (2 n - 1)}{n!} \times {(- 2)}^{n} \end{array}

Commonly asked questions

If $p$ is a real number and if the middle term in the expansion of ${(\frac{p}{2} + 2)}^{8}$ is 1120, find $p$ .

This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} G i v e n expression i s {(\frac{P}{2} + 2)}^{8} \\ N u m b e r o f t e r m s = 8 + 1 = 9 (o d d) \\ ∴ M i d d l e t e r m {(\frac{n + 1}{2})}^{t h} t e r m = \frac{9 + 1}{2} = \frac{10}{2} = 5^{t h} t e r m \\ T_{5} = T_{4 + 1} = {}_{8}{C_{4}} {(\frac{P}{2})}^{8 - 4} {(2)}^{4} \\ = {}_{8}{C_{4}} \frac{P^{4}}{2^{4}} \times 2^{4} = {}_{8}{C_{4}} P^{4} \\ N o w {}_{8}{C_{4}} P^{4} = 1120 \Rightarrow \frac{8 \times 7 \times 6 \times 5}{4 \times 3 \times 2 \times 1} . P^{4} = 1120 \\ \Rightarrow 70 P^{4} = 1120 \Rightarrow P^{4} = \frac{1120}{70} = 16 \\ \Rightarrow P^{4} = 2^{4} \Rightarrow P = \pm 2 \\ H e n c e, t h e r e q u i r e d v a l u e o f P = \pm 2 . \end{array}$

Show that the middle term in the expansion of (x – 1/x)²ⁿis 1 × 3 ×5 × … (2n -1)/n × (-2)ⁿ.

This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} G i v e n expression i s {(x - \frac{1}{x})}^{2 n} \\ N u m b e r o f t e r m s = 2 n + 1 = 9 (o d d) \\ ∴ M i d d l e t e r m {(\frac{n + 1}{2})}^{t h} t e r m = \frac{2 n + 1 + 1}{2} = (n + 1) t h t e r m . \\ G e n e r a l T e r m T_{r + 1} = {}_{n}{C_{r}} x^{n - r} y^{r} \\ ∴ T_{n + 1} = {}_{2 n}{C_{n}} {(x)}^{2 n - n} {(- \frac{1}{x})}^{n} = {}_{2 n}{C_{n}} {(x)}^{n} {(- 1)}^{n} . \frac{1}{x^{n}} \\ = {(- 1)}^{n} . {}_{2 n}{C_{n}} = {(- 1)}^{n} . \frac{2 n!}{n! (2 n - n)!} \\ = {(- 1)}^{n} . \frac{2 n!}{n! n!} = {(- 1)}^{n} . \frac{2 n (2 n - 1) (2 n - 2) (2 n - 3) \dots 1}{n! n (n - 1) (n - 2) (n - 3) \dots 1} \\ = {(- 1)}^{n} . \frac{2 n (2 n - 1) . 2 (n - 1) (2 n - 3) \dots 1}{n! n (n - 1) (n - 2) (n - 3) \dots 1} \\ = \frac{{(- 1)}^{n} . 2^{n} . [n (n - 1) (n - 1) \dots] . [(2 n - 1) . (2 n - 3) \dots 5.3.1]}{n! . n (n - 1) (n - 2) \dots 1} \\ = \frac{{(- 2)}^{n} [(2 n - 1) . (2 n - 3) \dots 5.3.1]}{n!} \\ = \frac{1 \times 3 \times 5 \times \dots (2 n - 1)}{n!} \times {(- 2)}^{n} \\ H e n c e, t h e m i d d l e t e r m = \frac{1 \times 3 \times 5 \times \dots (2 n - 1)}{n!} \times {(- 2)}^{n} \end{array}$

Find $n$ in the binomial expansion 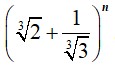$,$ if the ratio of the 7th term from the beginning to the 7th term from the end is $\frac{1}{6} .$

This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} T h e g i v e n expression i s {(+ \frac{1}{})}^{n} \\ = {(2^{1 / 3} + \frac{1}{3^{1 / 3}})}^{n} \\ G e n e r a l T e r m T_{r + 1} = {}_{n}{C_{r}} x^{n - r} y^{r} \\ T_{7} = T_{6 + 1} = {}_{n}{C_{6}} {(2^{\frac{1}{3}})}^{n - 6} {(\frac{1}{3^{\frac{1}{3}}})}^{6} \\ = {}_{n}{C_{6}} {(2)}^{\frac{n - 6}{3}} . (\frac{1}{3^{2}}) = {}_{n}{C_{6}} {(2)}^{\frac{n - 6}{3}} . {(3)}^{- 2} \\ 7 t h t e r m f r o m t h e e n d = {(n - 7 + 2)}^{t h} t e r m f r o m t h e b e g i n n i n g \\ = {(n - 5)}^{t h} t e r m f r o m t h e b e g i n n i n g \\ S o, T_{n - 6 + 1} = {}_{n}{C_{n - 6}} {(2^{\frac{1}{3}})}^{n - n + 6} {(\frac{1}{3^{\frac{1}{3}}})}^{n - 6} \\ = {}_{n}{C_{n - 6}} {(2)}^{2} . (\frac{1}{3^{\frac{n - 6}{3}}}) = {}_{n}{C_{n - 6}} {(2)}^{2} . {(3)}^{\frac{6 - n}{3}} \\ A c c o r d i n g t o t h e q u e s t i o n, w e g e t \\ \frac{{}_{n}{C_{6}} {(2)}^{\frac{n - 6}{3}} . {(3)}^{- 2}}{{}_{n}{C_{n - 6}} {(2)}^{2} . {(3)}^{\frac{6 - n}{3}}} = \frac{1}{6} \\ \Rightarrow \frac{{}_{n}{C_{n - 6}} {(2)}^{\frac{n - 6}{3}} . {(3)}^{- 2}}{{}_{n}{C_{n - 6}} {(2)}^{2} . {(3)}^{\frac{6 - n}{3}}} = \frac{1}{6} \Rightarrow {(2)}^{\frac{n - 6}{3} - 2} . {(3)}^{- 2 - \frac{6 - n}{3}} = \frac{1}{6} \\ \Rightarrow {(2)}^{\frac{n - 6 - 6}{3}} . {(3)}^{\frac{- 6 - 6 + n}{3}} = \frac{1}{6} \Rightarrow {(2)}^{\frac{n - 12}{3}} . {(3)}^{\frac{n - 12}{3}} = {(6)}^{- 1} \\ \Rightarrow {(6)}^{\frac{n - 12}{3}} = {(6)}^{- 1} \Rightarrow \frac{n - 12}{3} = - 1 \\ \Rightarrow n - 12 = - 3 \Rightarrow n = 12 - 3 = 9 \\ H e n c e, t h e r e q u i r e d v a l u e o f n i s 9 . \end{array}$

In the expansion of ${(x + a)}^{n}$ if the sum of odd terms is denoted by $O$ and the sum of even terms by $E$ , prove that:

$O^{2} - E^{2} = {(x^{2} - a^{2})}^{n} .$

$4 O E = {(x + a)}^{2 n} - {(x - a)}^{2 n} .$

This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} (i) T h e g i v e n expression i s {(x + a)}^{n} \\ {(x + a)}^{n} = {}_{n}{C_{0}} x^{n} a^{0} + {}_{n}{C_{1}} x^{n - 1} a + {}_{n}{C_{2}} x^{n - 2} a^{2} + {}_{n}{C_{3}} x^{n - 3} a^{3} + \dots + {}_{n}{C_{n}} a^{n} \\ S u m o f o d d t e r m s, \\ O = {}_{n}{C_{0}} x^{n} + {}_{n}{C_{2}} x^{n - 2} a^{2} + {}_{n}{C_{4}} x^{n - 4} a^{4} + \dots \\ a n d t h e s u m o f e v e n t e r m s, \\ E = {}_{n}{C_{1}} x^{n - 1} a + {}_{n}{C_{3}} x^{n - 3} a^{3} + {}_{n}{C_{5}} x^{n - 5} a^{5} + \dots \\ N o w {(x + a)}^{n} = O + E \dots (i) \\ S i m i l a r l y, {(x - a)}^{n} = O - E \dots (i i) \\ M u l t i p l y i n g e q n . (i) a n d e q n . (i i), w e g e t \\ {(x + a)}^{n} {(x - a)}^{n} = (O + E) (O - E) \\ {(x^{2} - a^{2})}^{n} = O^{2} - E^{2} \\ H e n c e, O^{2} - E^{2} = {(x^{2} - a^{2})}^{n} \\ (i i) 4 O E = {(O + E)}^{2} - {(O - E)}^{2} \\ = {[{(x + a)}^{n}]}^{2} - {[{(x - a)}^{n}]}^{2} \\ = {[x + a]}^{2 n} - {[x - a]}^{2 n} \\ H e n c e, 4 O E = {(x + a)}^{2 n} - {(x - a)}^{2 n} \end{array}$

If $x^{p}$ occurs in the expansion of ${(\frac{x^{2} + 1}{x})}^{2 n},$ prove that its coefficient is $\frac{4 n - p}{3} \frac{2 n + p}{3} .$

This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} T h e g i v e n expression i s {(x^{2} + \frac{1}{x})}^{2 n} \\ G e n e r a l T e r m T_{r + 1} = {}_{n}{C_{r}} x^{n - r} y^{r} \\ = {}_{2 n}{C_{r}} {(x^{2})}^{2 n - r} {(\frac{1}{x})}^{r} = {}_{2 n}{C_{r}} {(x)}^{4 n - 2 r} . \frac{1}{x^{r}} \\ = {}_{2 n}{C_{r}} {(x)}^{4 n - 2 r - r} = {}_{2 n}{C_{r}} {(x)}^{4 n - 3 r} \\ I f x^{p} o c c u r s i n {(x^{2} + \frac{1}{x})}^{2 n} \\ t h e n 4 n - 3 r = p \Rightarrow 3 r = 4 n - p \\ \Rightarrow r = \frac{4 n - p}{3} \\ ∴ C o e f f i c i e n t o f x^{p} = {}_{2 n}{C_{r}} = {}_{2 n}{C_{\frac{4 n - p}{3}}} \\ = \frac{(2 n)!}{(\frac{4 n - p}{3})! (2 n - \frac{4 n - p}{3})!} = \frac{(2 n)!}{(\frac{4 n - p}{3})! (\frac{6 n - 4 n + p}{3})!} \\ = \frac{(2 n)!}{(\frac{4 n - p}{3})! (\frac{2 n + p}{3})!} \\ H e n c e, c o e f f i c i e n t o f x^{p} = \frac{(2 n)!}{(\frac{4 n - p}{3})! (\frac{2 n + p}{3})!} \end{array}$

Find the term independent of $x$ in the expansion of ${(1 + x + 2 x^{3})}^{}$ 3/2 x² – 1/3x ⁹.

This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} T h e g i v e n expression i s (1 + x + 2 x^{3}) {(\frac{3}{2} x^{2} - \frac{1}{3 x})}^{9} \\ L e t u s c o n s i d e r {(\frac{3}{2} x^{2} - \frac{1}{3 x})}^{9} \\ G e n e r a l T e r m T_{r + 1} = {}_{n}{C_{r}} x^{n - r} y^{r} \\ T_{r + 1} = {}_{9}{C_{r}} {(\frac{3}{2} x^{2})}^{9 - r} {(- \frac{1}{3 x})}^{r} = {}_{9}{C_{r}} {(\frac{3}{2})}^{9 - r} {(x)}^{18 - 2 r} {(- \frac{1}{3})}^{r} . \frac{1}{x^{r}} \\ = {}_{9}{C_{r}} {(\frac{3}{2})}^{9 - r} {(x)}^{18 - 2 r - r} {(- \frac{1}{3})}^{r} = {}_{9}{C_{r}} {(\frac{3}{2})}^{9 - r} {(- \frac{1}{3})}^{r} . {(x)}^{18 - 3 r} \\ S o, t h e g e n e r a l t e r m i n t h e expansion o f \\ (1 + x + 2 x^{3}) {(\frac{3}{2} x^{2} - \frac{1}{3 x})}^{9} \\ = {}_{9}{C_{r}} {(\frac{3}{2})}^{9 - r} {(- \frac{1}{3})}^{r} . {(x)}^{18 - 3 r} + {}_{9}{C_{r}} {(\frac{3}{2})}^{9 - r} {(- \frac{1}{3})}^{r} . {(x)}^{19 - 3 r} + 2 . {}_{9}{C_{r}} {(\frac{3}{2})}^{9 - r} {(- \frac{1}{3})}^{r} . {(x)}^{21 - 3 r} \\ F o r g e t t i n g t h e t e r m i n d e p e n d e n t o f x, \\ P u t 18 - 3 r = 0, 19 - 3 r = 0 a n d 21 - 3 r = 0 w e g e t \\ r = 6, r = \frac{19}{3} a n d r = 7 \\ T h e p o s s i b l e v a l u e o f r a r e 6 a n d 7 (? r \neq \frac{19}{3}) \\ ∴ T h e t e r m i n d e p e n d e n t o f x i s \\ = {}_{9}{C_{6}} {(\frac{3}{2})}^{9 - 6} {(- \frac{1}{3})}^{6} + . {}_{9}{C_{7}} {(\frac{3}{2})}^{9 - 7} {(- \frac{1}{3})}^{7} \\ = \frac{9 \times 8 \times 7 \times 6!}{3 \times 2 \times 1 \times 6!} . \frac{3^{3}}{2^{3}} . \frac{1}{3^{6}} - 2 . \frac{9 \times 8 \times 7!}{2 \times 1 \times 7!} . \frac{3^{2}}{2^{2}} . \frac{1}{3^{7}} \\ = \frac{84}{8} . \frac{1}{3^{3}} - \frac{36}{4} . \frac{2}{3^{5}} = \frac{7}{18} - \frac{2}{27} = \frac{21 - 4}{54} = \frac{17}{54} \\ H e n c e, t h e r e q u i r e d t e r m i s \frac{17}{54} \end{array}$

Binomial Theorem Short Answer Type Questions

Find the term independent of x, $x \neq 0$ , in the expansion of (3x²/2 – 1/3x)¹⁵

\begin{array}{l} G e n e r a l T e r m T_{r + 1} = {}_{n}{C_{r}} x^{n - r} y^{r} \\ = {}_{15}{C_{r}} {(\frac{3 x^{2}}{2})}^{15 - r} {(- \frac{1}{3 x})}^{r} = {}_{15}{C_{r}} {(\frac{3}{2})}^{15 - r} {(x)}^{30 - 2 r} {(- \frac{1}{3})}^{r} \frac{1}{x^{r}} \\ = {}_{15}{C_{r}} {(\frac{3}{2})}^{15 - r} {(x)}^{30 - 2 r - r} {(- 1)}^{r} \frac{1}{{(3)}^{r}} \\ = {}_{15}{C_{r}} {(\frac{3}{2})}^{15 - r} {(x)}^{30 - 3 r} {(- 1)}^{r} \frac{1}{{(3)}^{r}} \\ f o r g e t t i n g t h e t e r m i n d e p e n d e n t o f x, \\ 30 - 3 r = 0 \Rightarrow r = 10 \\ O n p u t t i n g t h e v a l u e o f r i n t h e a b o v e expression, w e g e t \\ = {}_{15}{C_{10}} {(\frac{3}{2})}^{15 - 10} {(- 1)}^{10} \frac{1}{{(3)}^{10}} = {}_{15}{C_{10}} \frac{{(3)}^{5}}{{(2)}^{5}} . \frac{1}{{(3)}^{10}} \\ = {}_{15}{C_{10}} . \frac{1}{{(2)}^{5} . {(3)}^{5}} = {}_{15}{C_{10}} {(\frac{1}{6})}^{5} \\ H e n c e, t h e r e q u i r e d t e r m = {}_{15}{C_{10}} {(\frac{1}{6})}^{5} \end{array}

If the term free from in the expansion of x – k/x² ¹⁰is 405, find the value of .

\begin{array}{l} T h e g i v e n expression i s {(\sqrt[]{x} - \frac{K}{x^{2}})}^{10} \\ G e n e r a l T e r m T_{r + 1} = {}_{n}{C_{r}} x^{n - r} y^{r} \\ = {}_{10}{C_{r}} {(\sqrt[]{x})}^{10 - r} {(\frac{- K}{x^{2}})}^{r} = {}_{10}{C_{r}} {(x)}^{\frac{10 - r}{2}} {(- K)}^{r} (\frac{1}{x^{2 r}}) \\ = {}_{10}{C_{r}} {(x)}^{\frac{10 - r}{2} - 2 r} {(- K)}^{r} = {}_{10}{C_{r}} {(x)}^{\frac{10 - r - 4 r}{2}} {(- K)}^{r} \\ = {}_{10}{C_{r}} {(x)}^{\frac{10 - 5 r}{2}} {(- K)}^{r} \\ f o r g e t t i n g t h e t e r m i n d e p e n d e n t o f x, \\ \frac{10 - 5 r}{2} = 0 \Rightarrow r = 2 \\ O n p u t t i n g t h e v a l u e o f r i n t h e a b o v e expression, w e g e t \\ = {}_{10}{C_{2}} {(- K)}^{2} \\ A c c o r d i n g t o t h e c o n d i t i o n o f t h e q u e s t i o n, w e h a v e \\ {}_{10}{C_{2}} K^{2} = 405 \Rightarrow \frac{10.9}{2.1} K^{2} = 405 \\ \Rightarrow 45 K^{2} = 405 \Rightarrow K^{2} = \frac{405}{45} = 9 \\ ∴ K = \pm 3 \\ H e n c e, t h e v a l u e o f K = \pm 3 \end{array}

Commonly asked questions

Find the term independent of $x$ , $x \neq 0$ , in the expansion of (3x²/2 – 1/3x)¹⁵

This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} G e n e r a l T e r m T_{r + 1} = {}_{n}{C_{r}} x^{n - r} y^{r} \\ = {}_{15}{C_{r}} {(\frac{3 x^{2}}{2})}^{15 - r} {(- \frac{1}{3 x})}^{r} = {}_{15}{C_{r}} {(\frac{3}{2})}^{15 - r} {(x)}^{30 - 2 r} {(- \frac{1}{3})}^{r} \frac{1}{x^{r}} \\ = {}_{15}{C_{r}} {(\frac{3}{2})}^{15 - r} {(x)}^{30 - 2 r - r} {(- 1)}^{r} \frac{1}{{(3)}^{r}} \\ = {}_{15}{C_{r}} {(\frac{3}{2})}^{15 - r} {(x)}^{30 - 3 r} {(- 1)}^{r} \frac{1}{{(3)}^{r}} \\ f o r g e t t i n g t h e t e r m i n d e p e n d e n t o f x, \\ 30 - 3 r = 0 \Rightarrow r = 10 \\ O n p u t t i n g t h e v a l u e o f r i n t h e a b o v e expression, w e g e t \\ = {}_{15}{C_{10}} {(\frac{3}{2})}^{15 - 10} {(- 1)}^{10} \frac{1}{{(3)}^{10}} = {}_{15}{C_{10}} \frac{{(3)}^{5}}{{(2)}^{5}} . \frac{1}{{(3)}^{10}} \\ = {}_{15}{C_{10}} . \frac{1}{{(2)}^{5} . {(3)}^{5}} = {}_{15}{C_{10}} {(\frac{1}{6})}^{5} \\ H e n c e, t h e r e q u i r e d t e r m = {}_{15}{C_{10}} {(\frac{1}{6})}^{5} \end{array}$

If the term free from $x$ in the expansion of x – k/x² ¹⁰ is 405, find the value of $k$ .

This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} T h e g i v e n expression i s {(\sqrt[]{x} - \frac{K}{x^{2}})}^{10} \\ G e n e r a l T e r m T_{r + 1} = {}_{n}{C_{r}} x^{n - r} y^{r} \\ = {}_{10}{C_{r}} {(\sqrt[]{x})}^{10 - r} {(\frac{- K}{x^{2}})}^{r} = {}_{10}{C_{r}} {(x)}^{\frac{10 - r}{2}} {(- K)}^{r} (\frac{1}{x^{2 r}}) \\ = {}_{10}{C_{r}} {(x)}^{\frac{10 - r}{2} - 2 r} {(- K)}^{r} = {}_{10}{C_{r}} {(x)}^{\frac{10 - r - 4 r}{2}} {(- K)}^{r} \\ = {}_{10}{C_{r}} {(x)}^{\frac{10 - 5 r}{2}} {(- K)}^{r} \\ f o r g e t t i n g t h e t e r m i n d e p e n d e n t o f x, \\ \frac{10 - 5 r}{2} = 0 \Rightarrow r = 2 \\ O n p u t t i n g t h e v a l u e o f r i n t h e a b o v e expression, w e g e t \\ = {}_{10}{C_{2}} {(- K)}^{2} \\ A c c o r d i n g t o t h e c o n d i t i o n o f t h e q u e s t i o n, w e h a v e \\ {}_{10}{C_{2}} K^{2} = 405 \Rightarrow \frac{10.9}{2.1} K^{2} = 405 \\ \Rightarrow 45 K^{2} = 405 \Rightarrow K^{2} = \frac{405}{45} = 9 \\ ∴ K = \pm 3 \\ H e n c e, t h e v a l u e o f K = \pm 3 \end{array}$

Find the coefficient of $x$ in the expansion of

$(1 - 3 x + 7 x^{2}) {(1 - x)}^{16} .$

This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} T h e g i v e n expression i s (1 - 3 x + 7 x^{2}) {(1 - x)}^{16} \\ = (1 - 3 x + 7 x^{2}) [{}_{16}{C_{0}} {(1)}^{16} {(- x)}^{0} + {}_{16}{C_{1}} {(1)}^{15} (- x) + {}_{16}{C_{2}} {(1)}^{14} {(- x)}^{2} + \dots] \\ = (1 - 3 x + 7 x^{2}) (1 - 16 x + 120 x^{2} + \dots) \\ C o l l e c t i n g t h e t e r m c o n t a i n i n g x, w e g e t - 16 x - 3 x = - 19 x \\ H e n c e, t h e c o e f f i c i e n t o f x = - 19 \end{array}$

Find the term independent of $x$ in the expansion of 3x – 2/x^{2 15}

This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} G i v e n expression i s {(3 x - \frac{2}{x^{2}})}^{15} \\ G e n e r a l t e r m T_{r + 1} = {}_{n}{C_{r}} x^{n - r} y^{r} \\ = {}_{15}{C_{r}} {(3 x)}^{15 - r} {(- \frac{2}{x^{2}})}^{r} = {}_{15}{C_{r}} {(3)}^{15 - r} {(x)}^{15 - r} {(- 2)}^{r} . \frac{1}{x^{2 r}} \\ = {}_{15}{C_{r}} {(3)}^{15 - r} . {(x)}^{15 - r - 2 r} {(- 2)}^{r} \\ = {}_{15}{C_{r}} {(3)}^{15 - r} {(x)}^{15 - 3 r} {(- 2)}^{r} \\ f o r g e t t i n g t h e t e r m i n d e p e n d e n t o f x, \\ 15 - 3 r = 0 \Rightarrow r = 5 \\ O n p u t t i n g t h e v a l u e o f r i n t h e a b o v e expression, w e g e t \\ = {}_{15}{C_{5}} {(3)}^{15 - 5} {(- 2)}^{5} = - {}_{15}{C_{5}} {(3)}^{10} {(2)}^{5} \\ = - \frac{15 \times 14 \times 13 \times 12 \times 11}{5 \times 4 \times 3 \times 2 \times 1} . {(3)}^{10} {(2)}^{5} = - 7 \times 13 \times 3 \times 11 . {(3)}^{10} {(2)}^{5} = - 3003 . {(3)}^{10} {(2)}^{5} \\ H e n c e, t h e r e q u i r e d t e r m = - 3003 . {(3)}^{10} {(2)}^{5} \end{array}$

Find the middle term(s) in the expansion of:

${(x / a - \frac{a}{x})}^{10} .$ 3x – x³/6 ⁹

This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} (i) G i v e n expression i s {(\frac{x}{a} - \frac{a}{x})}^{10} \\ N u m b e r o f t e r m s = 10 + 1 = 11 (o d d) \\ ∴ M i d d l e t e r m {(\frac{n + 1}{2})}^{t h} t e r m = \frac{11 + 1}{2} = \frac{12}{2} = 6^{t h} t e r m \\ G e n e r a l t e r m T_{r + 1} = {}_{n}{C_{r}} x^{n - r} y^{r} \\ \Rightarrow T_{5 + 1} = {}_{10}{C_{5}} {(\frac{x}{a})}^{10 - 5} {(- \frac{a}{x})}^{5} = - {}_{10}{C_{5}} \frac{x^{5}}{a^{5}} . \frac{a^{5}}{x^{5}} = - {}_{10}{C_{5}} \\ = - \frac{10 \times 9 \times 8 \times 7 \times 6}{5 \times 4 \times 3 \times 2 \times 1} . = - 9 \times 7 \times 4 = - 252 \\ H e n c e, t h e r e q u i r e d m i d d l e t e r m = - 252 \\ (i i) G i v e n expression i s {(3 x - \frac{x^{3}}{6})}^{9} \\ N u m b e r o f t e r m s = 9 + 1 = 10 (e v e n) \\ ∴ M i d d l e t e r m s a r e {(\frac{n}{2})}^{t h} t e r m a n d {(\frac{n}{2} + 1)}^{t h} t e r m \\ {(\frac{10}{2})}^{t h} = 5^{t h} t e r m a n d {(\frac{10}{2} + 1)}^{t h} = 6^{t h} t e r m \\ G e n e r a l t e r m T_{r + 1} = {}_{n}{C_{r}} x^{n - r} y^{r} \\ ∴ T_{5} = T_{4 + 1} = {}_{9}{C_{4}} {(3 x)}^{9 - 4} {(- \frac{x^{3}}{6})}^{4} = {}_{9}{C_{4}} {(3)}^{5} . x^{5} {(- \frac{1}{6})}^{4} . x^{12} \\ = \frac{9 \times 8 \times 7 \times 6}{4 \times 3 \times 2 \times 1} \times \frac{3 \times 3 \times 3 \times 3 \times 3}{6 \times 6 \times 6 \times 6} x^{17} = \frac{189}{8} x^{17} \\ N o w, T_{6} = T_{5 + 1} = {}_{9}{C_{5}} {(3 x)}^{9 - 5} {(- \frac{x^{3}}{6})}^{5} \\ = {}_{9}{C_{5}} {(3)}^{4} . x^{4} {(- \frac{1}{6})}^{5} . x^{15} \\ = \frac{9 \times 8 \times 7 \times 6 \times 5}{5 \times 4 \times 3 \times 2 \times 1} {(3)}^{4} {(- \frac{1}{6})}^{5} . x^{19} = - \frac{21}{16} x^{19} \\ H e n c e, t h e r e q u i r e d m i d d l e t e r m s a r e \frac{189}{8} x^{17} a n d - \frac{21}{16} x^{19} \end{array}$

Find the coefficient of $x^{15}$ in the expansion of ${(x - x^{2})}^{10} .$

This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} T h e g i v e n expression i s {(x - x^{2})}^{10} \\ G e n e r a l T e r m T_{r + 1} = {}_{n}{C_{r}} x^{n - r} y^{r} \\ = {}_{10}{C_{r}} {(x)}^{10 - r} {(- x^{2})}^{r} = {}_{10}{C_{r}} {(x)}^{10 - r} {(- 1)}^{r} {(x^{2})}^{r} \\ = {(- 1)}^{r} . {}_{10}{C_{r}} {(x)}^{10 - r + 2 r} = {(- 1)}^{r} . {}_{10}{C_{r}} {(x)}^{10 + r} \\ T o f i n d t h e c o e f f i c i e n t o f x^{15}, P u t 10 + r = 15 \Rightarrow r = 5 \\ ∴ C o e f f i c i e n t o f x^{15} = {(- 1)}^{5} . {}_{10}{C_{5}} = - {}_{10}{C_{5}} = - 252 \\ H e n c e, t h e r e q u i r e d c o e f f i c i e n t = - 252 \end{array}$

Find the coefficient of $\frac{1}{x^{17}}$ in the expansion of x⁴– 1/x^{3 15}

This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} T h e g i v e n expression i s {(x^{4} - \frac{1}{x^{3}})}^{15} \\ G e n e r a l T e r m T_{r + 1} = {}_{n}{C_{r}} x^{n - r} y^{r} \\ = {}_{15}{C_{r}} {(x^{4})}^{15 - r} {(- \frac{1}{x^{3}})}^{r} = {}_{15}{C_{r}} {(x)}^{60 - 4 r} {(- 1)}^{r} . \frac{1}{{x^{3}}^{r}} \\ = {}_{15}{C_{r}} {(- 1)}^{r} . \frac{1}{{x^{3}}^{r - 60 + 4 r}} = {}_{15}{C_{r}} {(- 1)}^{r} . \frac{1}{{x^{7}}^{r - 60}} \\ T o f i n d t h e c o e f f i c i e n t o f \frac{1}{x^{17}}, P u t 7 r - 60 = 17 \Rightarrow 7 r = 60 + 11 \Rightarrow r = \frac{77}{7} = 11 \\ P u t t i n g t h e v a l u e o f r i n t h e a b o v e expression, w e g e t \\ = {}_{15}{C_{11}} {(- 1)}^{11} . \frac{1}{x^{17}} = - {}_{15}{C_{4}} . \frac{1}{x^{17}} = - \frac{15 \times 14 \times 13 \times 12}{4 \times 3 \times 2 \times 1} . \frac{1}{x^{17}} \\ = - 1365 . \frac{1}{x^{17}} \\ H e n c e, t h e r e q u i r e d c o e f f i c i e n t o f \frac{1}{x^{17}} = - 1365 \end{array}$

Find the sixth term of the expansion ${(y^{\frac{1}{2}} + x^{\frac{1}{3}})}^{n}$ , if the binomial coefficient of the third term from the end is 45.

[Hint: Binomial coefficient of third term from the end = Binomial coefficient of third term from the beginning = ⁿC₂.]

This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} T h e g i v e n expression i s {(y^{\frac{1}{2}} + x^{\frac{1}{3}})}^{n}, since t h e b i n o m i a l c o e f f i c i e n t o f t h i r d \\ t e r m f r o m t h e e n d = b i n o m i a l c o e f f i c i e n t o f t h i r d t e r m f r o m t h e b e g i n n i n g = {}_{n}{C_{2}} \\ ∴ {}_{n}{C_{2}} = 45 \\ \Rightarrow \frac{n (n - 1)}{2} = 45 \Rightarrow n^{2} - n = 90 \\ \Rightarrow n^{2} - n - 90 = 0 \Rightarrow n^{2} - 10 n + 9 n - 90 = 0 \\ \Rightarrow n (n - 10) + 9 (n - 10) = 0 \Rightarrow (n - 10) (n + 9) = 0 \\ \Rightarrow n = 10, n = - 9 \Rightarrow n = 10, n \neq - 9 \\ S o, t h e g i v e n expression b e c o m e s {(y^{\frac{1}{2}} + x^{\frac{1}{3}})}^{10} \\ S i x t h t e r m i n t h i s expression \\ T_{6} = T_{5 + 1} = {}_{10}{C_{5}} {(y^{\frac{1}{2}})}^{10 - 5} {(x^{\frac{1}{3}})}^{5} = {}_{10}{C_{5}} y^{\frac{5}{2}} . x^{\frac{5}{3}} \\ = 252 y^{\frac{5}{2}} . x^{\frac{5}{3}} \\ H e n c e, t h e r e q u i r e d t e r m = 252 y^{\frac{5}{2}} . x^{\frac{5}{3}} \end{array}$

Find the value of $r$ , if the coefficients of the (2r + 4)^th and ^th terms in the expansion of ${(1 + x)}^{18}$ are equal.

This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} G e n e r a l T e r m T_{r + 1} = {}_{n}{C_{r}} x^{n - r} y^{r} \\ F o r c o e f f i c i e n t s o f {(2 r + 4)}^{t h} t e r m, w e h a v e \\ T_{2 r + 4} = T_{2 r + 3 + 1} = {}_{18}{C_{2 r + 3}} {(1)}^{18 - 2 r - 3} . x^{2 r + 3} \\ ∴ C o e f f i c i e n t s o f {(2 r + 4)}^{t h} t e r m = {}_{18}{C_{2 r + 3}} \\ S i m i l a r l y, T_{r - 2} = T_{r - 3 + 1} = {}_{18}{C_{r - 3}} {(1)}^{18 - r + 3} . x^{r - 3} \\ ∴ C o e f f i c i e n t s o f {(r - 2)}^{t h} t e r m = {}_{18}{C_{r - 3}} \\ A s p e r t h e c o n d i t i o n o f t h e q u e s t i o n s, w e h a v e {}_{18}{C_{2 r + 3}} = {}_{18}{C_{r - 3}} \\ \Rightarrow 2 r + 3 + r - 3 = 18 \Rightarrow 3 r = 18 \Rightarrow r = 6 \end{array}$

If the coefficient of second, third, and fourth terms in the expansion of ${(1 + x)}^{2 n}$ are in A.P. Show that $2 n^{2} - 9 n + 7 = 0 .$

This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} G i v e n expression i s {(1 + x)}^{2 n} \\ H e r e, c o e f f i c i e n t o f 2 n d t e r m = {}_{2 n}{C_{1}} \\ C o e f f i c i e n t o f 3 r d t e r m = {}_{2 n}{C_{2}} \\ a n d c o e f f i c i e n t o f 4 t h t e r m = {}_{2 n}{C_{3}} \\ G i v e n t h a t {}_{2 n}{C_{1}}, {}_{2 n}{C_{2}} a n d {}_{2 n}{C_{3}} a r e i n A . P \\ ∴ {}_{2 n}{C_{2}} - {}_{2 n}{C_{1}} = {}_{2 n}{C_{3}} - {}_{2 n}{C_{2}} \\ \Rightarrow 2 . {}_{2 n}{C_{2}} = {}_{2 n}{C_{1}} + {}_{2 n}{C_{3}} \\ \Rightarrow 2 . \frac{2 n!}{2! (2 n - 2)!} = \frac{2 n!}{(2 n - 1)!} + \frac{2 n!}{3! (2 n - 3)!} \\ \Rightarrow 2 [\frac{2 n (2 n - 1) (2 n - 2)!}{2 \times 1 \times (2 n - 2)!}] = \frac{2 n (2 n - 1)!}{(2 n - 1)!} + \frac{2 n (2 n - 1) (2 n - 2) (2 n - 3)!}{3 \times 2 \times 1 \times (2 n - 3)!} \\ \Rightarrow n (2 n - 1) = n + \frac{n (2 n - 1) (2 n - 2)}{6} \\ \Rightarrow 2 n - 1 = 1 + \frac{(2 n - 1) (2 n - 2)}{6} \\ \Rightarrow 12 n - 6 = 6 + 4 n^{2} - 4 n - 2 n + 2 \\ \Rightarrow 12 n - 12 = 4 n^{2} - 6 n + 2 \\ \Rightarrow 4 n^{2} - 6 n - 12 n + 2 + 12 = 0 \\ \Rightarrow 4 n^{2} - 18 n + 14 = 0 \\ \Rightarrow 2 n^{2} - 9 n + 7 = 0 \\ H e n c e p r o v e d . \end{array}$

Find the coefficient of $x^{4}$ in the expansion of ${(1 + x + x^{2} + x^{3})}^{11} .$

This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} G i v e n expression i s {(1 + x + x^{2} + x^{3})}^{11} \\ = {[(1 + x) + x^{2} (1 + x)]}^{11} = {[(1 + x) (1 + x^{2})]}^{11} \\ = {(1 + x)}^{11} . {(1 + x^{2})}^{11} \\ E x p a n d i n g t h e a b o v e expression, w e g e t \\ ({}_{11}{C_{0}} + {}_{11}{C_{1}} x + {}_{11}{C_{2}} x^{2} + {}_{11}{C_{3}} x^{3} + {}_{11}{C_{4}} x^{4} + \dots) . ({}_{11}{C_{0}} + {}_{11}{C_{1}} x^{2} + {}_{11}{C_{2}} x^{4} + \dots) \\ = (1 + 11 x + 55 x^{2} + 165 x^{3} + 330 x^{4} + \dots) . (1 + 11 x^{2} + 55 x^{4} + \dots) \\ C o l l e c t i n g t h e t e r m s c o n t a i n i n g x^{4}, w e g e t \\ (55 + 605 + 330) x^{4} = 990 x^{4} \\ H e n c e, t h e c o e f f i c i e n t o f x^{4} = 990 \end{array}$

Binomial Theorem Objective Type Questions

The total number of terms in the expansion of ${(x + a)}^{100} + {(x - a)}^{100}$ after simplification is:

(a) 50

(b) 202

(c) 51

(d) None of these

\begin{array}{l} N u m b e r o f t e r m s i n t h e expansion o f {(x + a)}^{100} = 101 \\ N u m b e r o f t e r m s i n t h e expansion o f {(x - a)}^{100} = 101 \\ N o w 50 t e r m s o f expansion w i l l c a n c e l o u t w i t h n e g a t i v e 50 t e r m s o f {(x - a)}^{100} \\ S o, t h e r e m a i n i n g 51 t e r m s o f f i r s t expansion w i l l b e a d d e d t o 51 t e r m s o f o t h e r . \\ T h e r e f o r e, t h e n u m b e r o f t e r m s = 51 \\ H e n c e, t h e c o r r e c t o p t i o n i s (c) . \end{array}

Given the integers $r > 1, n > 2$ , and the coefficients of the $(3 r)$ th and $(r + 2)$ nd terms in the binomial expansion of ${(1 + x)}^{2 n}$ are equal, then:

(a) $n = 2 r$

(b) $n = 3 r$

(c) $n = 2 r + 1$

(d) None of these

\begin{array}{l} G i v e n t h a t r > 1 a n d n > 2 \\ t h e n T_{3 r} = T_{3 r - 1 + 1} = {}_{2 n}{C_{3 r - 1}} . x^{3 r - 1} \\ a n d T_{r + 2} = T_{r + 1 + 1} = {}_{2 n}{C_{r + 1}} . x^{r + 1} \\ A s p e r q u e s t i o n, w e h a v e \\ {}_{2 n}{C_{3 r - 1}} = {}_{2 n}{C_{r + 1}} \\ \Rightarrow 3 r - 1 + r + 1 = 2 n [∵ {}_{n}{C_{p}} = {}_{n}{C_{q}} \Rightarrow n = p + q] \\ \Rightarrow 4 r = 2 n \\ \Rightarrow n = 2 r \\ H e n c e, t h e c o r r e c t o p t i o n i s (a) . \end{array}

Commonly asked questions

The total number of terms in the expansion of ${(x + a)}^{100} + {(x - a)}^{100}$ after simplification is:

(a) 50

(b) 202

(c) 51

(d) None of these

This is a Objective Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} N u m b e r o f t e r m s i n t h e expansion o f {(x + a)}^{100} = 101 \\ N u m b e r o f t e r m s i n t h e expansion o f {(x - a)}^{100} = 101 \\ N o w 50 t e r m s o f expansion w i l l c a n c e l o u t w i t h n e g a t i v e 50 t e r m s o f {(x - a)}^{100} \\ S o, t h e r e m a i n i n g 51 t e r m s o f f i r s t expansion w i l l b e a d d e d t o 51 t e r m s o f o t h e r . \\ T h e r e f o r e, t h e n u m b e r o f t e r m s = 51 \\ H e n c e, t h e c o r r e c t o p t i o n i s (c) . \end{array}$

Given the integers $r > 1, n > 2$ , and the coefficients of the $(3 r)$ th and $(r + 2)$ nd terms in the binomial expansion of ${(1 + x)}^{2 n}$ are equal, then:

(a) $n = 2 r$

(b) $n = 3 r$

(c) $n = 2 r + 1$

(d) None of these

This is a Objective Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} G i v e n t h a t r > 1 a n d n > 2 \\ t h e n T_{3 r} = T_{3 r - 1 + 1} = {}_{2 n}{C_{3 r - 1}} . x^{3 r - 1} \\ a n d T_{r + 2} = T_{r + 1 + 1} = {}_{2 n}{C_{r + 1}} . x^{r + 1} \\ A s p e r q u e s t i o n, w e h a v e \\ {}_{2 n}{C_{3 r - 1}} = {}_{2 n}{C_{r + 1}} \\ \Rightarrow 3 r - 1 + r + 1 = 2 n [? {}_{n}{C_{p}} = {}_{n}{C_{q}} \Rightarrow n = p + q] \\ \Rightarrow 4 r = 2 n \\ \Rightarrow n = 2 r \\ H e n c e, t h e c o r r e c t o p t i o n i s (a) . \end{array}$

The two successive terms in the expansion of ${(1 + x)}^{24}$ whose coefficients are in the ratio 1:4 are:

(a) 3^rd and 4^th

(b) 4^th and 5^th

(c) 5^th and 6^th

(d) 6^th and 7^th

This is a Objective Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} L e t r^{t h} a n d {(r + 1)}^{t h} b e t w o s u c c e s s i v e t e r m s i n t h e expansion {(1 + x)}^{24} \\ ∴ T_{r + 1} = {}_{24}{C_{r}} . x^{r} \\ a n d T_{r + 2} = T_{r + 1 + 1} = {}_{24}{C_{r + 1}} . x^{r + 1} \\ A s p e r q u e s t i o n, w e h a v e \frac{{}_{24}{C_{r}}}{{}_{24}{C_{r + 1}}} = \frac{1}{4} \\ \Rightarrow \frac{\frac{24!}{r! (24 - r)!}}{\frac{24!}{(r + 1)! (24 - r - 1)!}} = \frac{1}{4} \\ \Rightarrow \frac{24!}{r! (24 - r)!} \times \frac{(r + 1)! (24 - r - 1)!}{24!} = \frac{1}{4} \\ \Rightarrow \frac{(r + 1) . r! (24 - r - 1)!}{r! (24 - r) (24 - r - 1)!} = \frac{1}{4} \\ \Rightarrow \frac{r + 1}{24 - r} = \frac{1}{4} \Rightarrow 4 r + 4 = 24 - r \\ \Rightarrow 5 r = 20 \Rightarrow r = 4 \\ ∴ T_{4 + 1} = T_{5} a n d T_{4 + 2} = T_{6} \\ H e n c e, t h e c o r r e c t o p t i o n i s (c) . \end{array}$

The coefficient of $x^{n}$ in the expansion of ${(1 + x)}^{2 n}$ and ${(1 + x)}^{2 n - 1}$ are in the ratio:

(a) 1:2

(b) 1:3

(c) 3:1

(d) 2:1

This is a Objective Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} G e n e r a l T e r m T_{r + 1} = {}_{n}{C_{r}} x^{n - r} y^{r} \\ I n t h e expansion o f {(1 + x)}^{2 n}, w e g e t T_{r + 1} = {}_{2 n}{C_{r}} . x^{r} \\ T o g e t t h e c o e f f i c i e n t s o f x^{n}, p u t r = n \\ ∴ C o e f f i c i e n t s o f x^{n} = {}_{2 n}{C_{n}} \\ I n t h e expansion o f {(1 + x)}^{2 n - 1}, w e g e t T_{r + 1} = {}_{2 n - 1}{C_{r}} . x^{r} \\ ∴ C o e f f i c i e n t s o f x^{n} = {}_{2 n - 1}{C_{n - 1}} \\ T h e r e q u i r e d r a t i o i s \frac{{}_{2 n}{C_{n}}}{{}_{2 n - 1}{C_{n - 1}}} \\ = \frac{\frac{2 n!}{n! (n)!}}{\frac{(2 n - 1)!}{(n - 1)! (2 n - 1 - n + 1)!}} = \frac{\frac{2 n!}{n! n!}}{\frac{(2 n - 1)!}{(n - 1)! (n)!}} \\ = \frac{2 n!}{n! n!} \times \frac{(n - 1)! n!}{(2 n - 1)!} = \frac{2 n (2 n - 1)!}{n! n (n - 1)!} \times \frac{(n - 1)! n!}{(2 n - 1)!} \\ = \frac{2}{1} = 2 : 1 \\ H e n c e, t h e c o r r e c t o p t i o n i s (d) . \end{array}$

If the coefficients of the 2nd, 3rd, and 4th terms in the expansion of ${(1 + x)}^{n}$ are in A.P., then the value of $n$ is:

(a) 2

(b) 7

(c) 11

(d) 14

[Hint: 2 ⁿC₂ = ⁿC₁ + ⁿC₃ $\Rightarrow n^{2} - 9 n + 14 = 0 \Rightarrow n = 27 .$ ]

This is a Objective Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} G i v e n expression i s {(1 + x)}^{n} \\ {(1 + x)}^{n} = {}_{n}{C_{0}} + {}_{n}{C_{1}} x + {}_{n}{C_{2}} x^{2} + {}_{n}{C_{3}} x^{3} + \dots + {}_{n}{C_{n}} x^{n} \\ H e r e, c o e f f i c i e n t o f 2 n d t e r m = {}_{n}{C_{1}} \\ C o e f f i c i e n t o f 3 r d t e r m = {}_{n}{C_{2}} \\ a n d c o e f f i c i e n t o f 4 t h t e r m = {}_{n}{C_{3}} \\ G i v e n t h a t {}_{n}{C_{1}}, {}_{n}{C_{2}} a n d {}_{n}{C_{3}} a r e i n A . P \\ ∴ 2 . {}_{n}{C_{2}} = {}_{n}{C_{1}} + {}_{n}{C_{3}} \\ \Rightarrow 2 . \frac{n (n - 1)}{2} = n + \frac{n (n - 1) (n - 2)}{3.2.1} \\ \Rightarrow n (n - 1) = n + \frac{n (n - 1) (n - 2)}{6} \\ \Rightarrow n - 1 = 1 + \frac{(n - 1) (n - 2)}{6} \\ \Rightarrow 6 n - 6 = 6 + n^{2} - 3 n + 2 \\ \Rightarrow n^{2} - 3 n - 6 n + 14 = 0 \\ \Rightarrow n^{2} - 9 n + 14 = 0 \Rightarrow n^{2} - 7 n - 2 n + 14 = 0 \\ \Rightarrow n (n - 7) - 2 (n - 7) = 0 \Rightarrow (n - 2) (n - 7) = 0 \\ \Rightarrow n = 2, 7 \Rightarrow n = 7 w h e r e a s n = 2 i s n o t p o s s i b l e \\ H e n c e, t h e c o r r e c t o p t i o n i s (b) . \end{array}$

If $A$ and $B$ are coefficients of $x^{n}$ in the expansions of ${(1 + x)}^{2 n}$ and ${(1 + x)}^{2 n - 1}$ , respectively, then $\frac{A}{B}$

(a) 1

(b) 2

(c) $\frac{1}{2}$

(d) $\frac{1}{n}$

[Hint: $\frac{A}{B} =$ ²ⁿC_n/^{2n – 1}C_n = 2]

This is a Objective Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} G i v e n expression i s {(1 + x)}^{2 n} \\ T_{r + 1} = {}_{2 n}{C_{r}} x^{r} \\ ∴ C o e f f i c i e n t o f x^{n} = {}_{2 n}{C_{n}} = A (G i v e n) \\ I n t h e expression i s {(1 + x)}^{2 n - 1} \\ T_{r + 1} = {}_{2 n - 1}{C_{r}} x^{r} \\ ∴ C o e f f i c i e n t o f x^{n} = {}_{2 n - 1}{C_{n - 1}} = B (G i v e n) \\ S o, \frac{A}{B} = \frac{{}_{2 n}{C_{n}}}{{}_{2 n - 1}{C_{n - 1}}} \\ = \frac{\frac{2 n!}{n! (n)!}}{\frac{(2 n - 1)!}{(n - 1)! (2 n - 1 - n + 1)!}} = \frac{\frac{2 n!}{n! n!}}{\frac{(2 n - 1)!}{(n - 1)! (n)!}} \\ = \frac{2 n!}{n! n!} \times \frac{(n - 1)! n!}{(2 n - 1)!} = \frac{2 n (2 n - 1)!}{n! n (n - 1)!} \times \frac{(n - 1)! n!}{(2 n - 1)!} \\ = \frac{2}{1} = 2 : 1 \\ H e n c e, t h e c o r r e c t o p t i o n i s (b) . \end{array}$

If the middle term of ${(1 + \frac{x sin x}{x})}^{10}$ is equal to $7 \frac{7}{8}$ , then the value of $x$ is:

(a) $2 n π + \frac{π}{6}$

(b) $n π + \frac{π}{6}$

(c) $n π + {(- 1)}^{n} \frac{π}{6}$

(d) $n π + {(- 1)}^{n} \frac{π}{3}$

[Hint: T₆ = ¹⁰C₅ 1/x₅ . x⁵ sin⁵ x = 63/3 = sin⁵ x = 1/25 sin ½= x = nπ + (-1)ⁿπ/6]

This is a Objective Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} G i v e n expression i s {(\frac{1}{x} + x s i n x)}^{10} \\ N u m b e r o f t e r m s = 10 + 1 = 11 (o d d) \\ ∴ M i d d l e t e r m {(\frac{n + 1}{2})}^{t h} t e r m = \frac{11 + 1}{2} = \frac{12}{2} = 6^{t h} t e r m \\ T_{6} = T_{5 + 1} = {}_{10}{C_{5}} {(\frac{1}{x})}^{10 - 5} {(x s i n x)}^{5} \\ ∴ {}_{10}{C_{5}} {(\frac{1}{x})}^{5} . x^{5} . s i n^{5} x = 7 \frac{7}{8} \Rightarrow {}_{10}{C_{5}} . s i n^{5} x = \frac{63}{8} \\ \Rightarrow \frac{10 \times 9 \times 8 \times 7 \times 6}{5 \times 4 \times 3 \times 2 \times 1} . s i n^{5} x = \frac{63}{8} \Rightarrow 252 . s i n^{5} x = \frac{63}{8} \\ \Rightarrow s i n^{5} x = \frac{63}{8 \times 252} \Rightarrow s i n^{5} x = \frac{1}{32} \\ \Rightarrow s i n^{5} x = {(\frac{1}{2})}^{5} \Rightarrow s i n x = \frac{1}{2} \\ \Rightarrow s i n x = s i n \frac{π}{6} \\ ∴ x = n π + {(- 1)}^{n} . \frac{π}{6} \\ H e n c e, t h e c o r r e c t o p t i o n i s (c) . \end{array}$

Binomial Theorem Fill in the Blanks

The largest coefficient in the expansion of ${(1 + x)}^{30}$ is _________________ .

\begin{array}{l} H e r e n = 30 w h i c h i s e v e n \\ ∴ t h e largest c o e f f i c i e n t i n {(1 + x)}^{n} = {}_{n}{C_{n / 2}} \\ S o, t h e largest c o e f f i c i e n t i n {(1 + x)}^{30} = {}_{30}{C_{15}} \\ H e n c e, t h e v a l u e o f t h e f i l l e r i s {}_{30}{C_{15}} . \end{array}

The number of terms in the expansion of ${(x + y + z)}^{n}$ is _________________

[Hint: ${(x + y + z)}^{n} = {[x + (y + z)]}^{n} .$ ]

\begin{array}{l} T h e expression {(x + y + z)}^{n} c a n b e w r i t t e n a {[x + (y + z)]}^{n} \\ ∴ {[x + (y + z)]}^{n} = {}_{n}{C_{0}} x^{n} {(y + z)}^{0} + {}_{n}{C_{1}} {(x)}^{n - 1} (y + z) + {}_{n}{C_{2}} {(x)}^{n - 2} {(y + z)}^{2} + \dots + {}_{n}{C_{n}} {(y + z)}^{n} \\ ∴ N u m b e r o f t e r m s 1 + 2 + 3 + 4 + \dots + (n + 1) = \frac{(n + 1) (n + 2)}{2} \\ H e n c e, t h e v a l u e o f t h e f i l l e r i s \frac{(n + 1) (n + 2)}{2} \end{array}

Commonly asked questions

The largest coefficient in the expansion of ${(1 + x)}^{30}$ is _________________ .

This is a Fill in the Blanks Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} H e r e n = 30 w h i c h i s e v e n \\ ∴ t h e the largest c o e f f i c i e n t i n {(1 + x)}^{n} = {}_{n}{C_{n / 2}} \\ S o, t h e the largest c o e f f i c i e n t i n {(1 + x)}^{30} = {}_{30}{C_{15}} \\ H e n c e, t h e v a l u e o f t h e f i l l e r i s {}_{30}{C_{15}} . \end{array}$

The number of terms in the expansion of ${(x + y + z)}^{n}$ is _________________

[Hint: ${(x + y + z)}^{n} = {[x + (y + z)]}^{n} .$ ]

This is a Fill in the Blanks Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} T h e expression {(x + y + z)}^{n} c a n b e w r i t t e n a {[x + (y + z)]}^{n} \\ ∴ {[x + (y + z)]}^{n} = {}_{n}{C_{0}} x^{n} {(y + z)}^{0} + {}_{n}{C_{1}} {(x)}^{n - 1} (y + z) + {}_{n}{C_{2}} {(x)}^{n - 2} {(y + z)}^{2} + \dots + {}_{n}{C_{n}} {(y + z)}^{n} \\ ∴ N u m b e r o f t e r m s 1 + 2 + 3 + 4 + \dots + (n + 1) = \frac{(n + 1) (n + 2)}{2} \\ H e n c e, t h e v a l u e o f t h e f i l l e r i s \frac{(n + 1) (n + 2)}{2} \end{array}$

In the expansion of x² – 1/x² ¹⁶ $,$ the value of the constant term is ________________ .

This is a Fill in the Blanks Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} L e t T_{r + 1} b e t h e c o n s t a n t t e r m i n t h e expansion o f {(x^{2} - \frac{1}{x^{2}})}^{16} \\ ∴ T_{r + 1} = {}_{16}{C_{r}} {(x^{2})}^{16 - r} {(\frac{- 1}{x^{2}})}^{r} = {}_{16}{C_{r}} {(x)}^{32 - 2 r} {(- 1)}^{r} . \frac{1}{x^{2 r}} \\ = {(- 1)}^{r} . {}_{16}{C_{r}} {(x)}^{32 - 2 r - 2 r} = {(- 1)}^{r} . {}_{16}{C_{r}} {(x)}^{32 - 4 r} \\ F o r g e t t i n g c o n s t a n t t e r m, 32 - 4 r = 0 \\ \Rightarrow r = 8 \\ ∴ T_{r + 1} = {(- 1)}^{8} . {}_{16}{C_{8}} = {}_{16}{C_{8}} \\ H e n c e, t h e v a l u e o f t h e f i l l e r i s {}_{16}{C_{8}} . \end{array}$

If the seventh terms from the beginning and the end in the expansion of 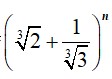are equal, then $n$ equals _________________ .

[Hint: $T_{7} = T_{n - 7 + 2}$ , = ⁿC⁶ (2 /3)^n-6 (1/3 ^{1/3 6}) = ⁿC^{n – 6} (2 ^1/3 ⁶ (1/3 ^1/3) ⁿ^{- 6} solve for $n .$ ]

= (2 ^1/3)ⁿ^{– 12} = 1/3 ^{1/3 n -12} = only problem when n – 12 = 0 = n =12].

This is a Fill in the Blanks Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} T h e g i v e n expansion i s {(+ \frac{1}{})}^{n} \\ ∴ T_{7} = T_{6 + 1} = {}_{n}{C_{6}} {(2^{1 / 3})}^{n - 6} . \frac{1}{{(3^{1 / 3})}^{6}} = {}_{n}{C_{6}} {(2)}^{\frac{n - 6}{3}} {(- 1)}^{r} . \frac{1}{{(3)}^{2}} \\ N o w t h e T_{7} f r o m t h e e n d = T_{7} f r o m t h e b e g i n n i n g i n {(\frac{1}{} +)}^{n} . \\ ∴ T_{7} = T_{6 + 1} = {}_{n}{C_{6}} {(\frac{1}{3^{1 / 3}})}^{n - 6} . {(2^{1 / 3})}^{6} \\ A s p e r t h e q u e s t i o n s, w e g e t \\ {}_{n}{C_{6}} {(2)}^{\frac{n - 6}{3}} . (\frac{1}{3^{2}}) = {}_{n}{C_{6}} . \frac{1}{3^{\frac{n - 6}{3}}} . {(2)}^{2} \\ \Rightarrow {(2)}^{\frac{n - 6}{3}} . {(3)}^{- 2} = {(3)}^{- (\frac{n - 6}{3})} . {(2)}^{2} \\ \Rightarrow {(2)}^{\frac{n - 6}{3} - 2} . {(3)}^{- 2 + \frac{n - 6}{3}} = 1 \\ \Rightarrow {(2)}^{\frac{n - 12}{3}} . {(3)}^{\frac{n - 12}{3}} = 1 \\ \Rightarrow {(6)}^{\frac{n - 12}{3}} = {(6)}^{0} \\ \Rightarrow \frac{n - 12}{3} = 0 \Rightarrow n = 12 \\ H e n c e, t h e v a l u e o f t h e f i l l e r i s 12 . \end{array}$

The coefficient of $a^{- 6} b^{4}$ in the expansion of ${(\frac{1}{a} + \frac{2 b}{3})}^{10}$ is _________________ .

[Hint: T₅ = ¹⁰C₄ 1/a ^b -2b/3 ⁴ = 1120/27 a^-6b⁴]

This is a Fill in the Blanks Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} T h e g i v e n expansion i s {(\frac{1}{a} - \frac{2 b}{3})}^{10} \\ F r o m a^{- 6} b^{4}, w e c a n t a k e r = 4 \\ ∴ T_{5} = T_{4 + 1} = {}_{10}{C_{4}} {(\frac{1}{a})}^{10 - 4} . {(- \frac{2 b}{3})}^{4} = {}_{10}{C_{4}} {(\frac{1}{a})}^{6} . {(- \frac{2}{3})}^{4} . b^{4} \\ = \frac{10.9.8.7}{4.3.2.1} \times \frac{16}{81} . a^{- 6} b^{4} = 210 \times \frac{16}{81} . a^{- 6} b^{4} \\ = \frac{1120}{27} . a^{- 6} b^{4} \\ H e n c e, t h e v a l u e o f t h e f i l l e r i s \frac{1120}{27} . \end{array}$

The middle term in the expansion of ${(a^{3} + b a)}^{28}$ is _________________ .

This is a Fill in the Blanks Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} N u m b e r o f t e r m s i n t h e expansion {(a^{3} + b a)}^{28} = 28 + 1 = 29 (o d d) \\ ∴ M i d d l e t e r m = \frac{29 + 1}{2} = 1 5^{t h} t e r m \\ ∴ T_{15} = T_{14 + 1} = {}_{28}{C_{14}} {(a^{3})}^{28 - 14} . {(b a)}^{14} = {}_{28}{C_{14}} {(a)}^{42} . b^{14} . a^{14} \\ = {}_{28}{C_{14}} a^{56} . b^{14} \\ H e n c e, t h e v a l u e o f t h e f i l l e r i s {}_{28}{C_{14}} a^{56} . b^{14} . \end{array}$

The ratio of the coefficients of $x^{p}$ and $x^{q}$ in the expansion of ${(1 + x)}^{p + q}$ is _________________ .

[Hint: : ^p^{+ q}C_p = ^p^{+ q}C_q

This is a Fill in the Blanks Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} G i v e n expansion i s {(1 + x)}^{p + q} \\ T_{r + 1} = {}_{p + q}{C_{r}} x^{r} \\ P u t r = p \\ = {}_{p + q}{C_{p}} x^{p} \\ ∴ t h e c o e f f i c i e n t s o f x^{p} = {}_{p + q}{C_{p}} \\ S i m i l a r l y, c o e f f i c i e n t s o f x^{q} = {}_{p + q}{C_{q}} \\ {}_{p + q}{C_{p}} = \frac{(p + q)!}{p! (p + q - p)!} = \frac{(p + q)!}{p! q!} \\ a n d {}_{p + q}{C_{q}} = \frac{(p + q)!}{q! (p + q - q)!} = \frac{(p + q)!}{p! q!} \\ S o, t h e r a t i o i s 1 : 1 . \end{array}$

The position of the term independent of $x$ in the expansion of $\sqrt {\frac{x}{3} + \frac{3}{{2 x}^{2}}}^{10}$ is _________________ .

This is a Fill in the Blanks Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} T h e g i v e n expansion i s {(\sqrt[]{\frac{x}{3}} + \frac{3}{2 x^{2}})}^{10} \\ T_{r + 1} = {}_{10}{C_{r}} {(\sqrt[]{\frac{x}{3}})}^{10 - r} {(\frac{3}{2 x^{2}})}^{r} = {}_{10}{C_{r}} {(\frac{x}{3})}^{\frac{10 - r}{2}} {(\frac{3}{2})}^{r} . \frac{1}{x^{2 r}} \\ = {}_{10}{C_{r}} {(\frac{1}{3})}^{\frac{10 - r}{2}} . x^{\frac{10 - r}{2}} {(\frac{3}{2})}^{r} . \frac{1}{x^{2 r}} \\ = {}_{10}{C_{r}} {(\frac{1}{3})}^{\frac{10 - r}{2}} . x^{\frac{10 - r}{2} - 2 r} {(\frac{3}{2})}^{r} \\ = {}_{10}{C_{r}} {(\frac{1}{3})}^{\frac{10 - r}{2}} . x^{\frac{10 - r - 4 r}{2}} {(\frac{3}{2})}^{r} \\ F o r i n d e p e n d e n t o f x, w e g e t \\ \frac{10 - r - 4 r}{2} = 0 \Rightarrow 10 - 5 r = 0 \Rightarrow r = 2 \\ S o, t h e p o s i t i o n o f t h e t e r m i n d e p e n d e n t o f x i s 3 r d t e r m . \\ H e n c e, t h e v a l u e o f t h e f i l l e r i s T h i r d t e r m . \end{array}$

If 2515 is divided by 13, the remainder is _________________ .

This is a Fill in the Blanks Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} L e t 2 5^{15} = {(26 - 1)}^{15} \\ = {}_{15}{C_{0}} {(26)}^{15} {(- 1)}^{0} + {}_{15}{C_{1}} {(26)}^{14} {(- 1)}^{1} + {}_{15}{C_{2}} {(26)}^{13} {(- 1)}^{2} + \dots + {}_{15}{C_{15}} {(- 1)}^{15} \\ = 2 6^{15} - 15 {(26)}^{14} + \dots - 1 - 13 + 13 \\ = 2 6^{15} - 15 {(26)}^{14} + \dots - 13 + 12 \\ = 13 λ + 12 \\ ∴ T h e r e m a i n d e r = 12 \\ H e n c e, t h e v a l u e o f t h e f i l l e r i s 12 . \end{array}$

Binomial Theorem True or False Type Questions

The sum of the series ^{10 20} _{r =0} C_ris 2¹⁹ + ²⁰ C₁₀/2

\begin{array}{l} \sum_{r = 0}^{10} {}_{20}{C_{r}} = {}_{20}{C_{0}} + {}_{20}{C_{1}} + {}_{20}{C_{2}} + {}_{20}{C_{3}} + \dots + {}_{20}{C_{10}} \\ = {}_{20}{C_{0}} + {}_{20}{C_{1}} + \dots + {}_{20}{C_{10}} + {}_{20}{C_{11}} + \dots + {}_{20}{C_{20}} - ({}_{20}{C_{11}} + \dots + {}_{20}{C_{20}}) \\ = 2^{20} - ({}_{20}{C_{11}} + \dots + {}_{20}{C_{20}}) \\ H e n c e, t h e g i v e n s t a t e m e n t i s' F a l s e' \end{array}

The expression $7^{9} + 9^{7}$ is divisible by 64.

[Hint: $7^{9} + 9^{7} = {(1 + 8)}^{9} - {(1 - 8)}^{7}$ .]

\begin{array}{l} 7^{9} + 9^{7} = {(1 + 8)}^{7} - {(1 - 8)}^{9} \\ = [{}_{7}{C_{0}} + {}_{7}{C_{1}} . 8 + {}_{7}{C_{2}} {(8)}^{2} + {}_{7}{C_{3}} {(8)}^{3} + \dots + {}_{7}{C_{7}} {(8)}^{7}] - [\begin{array}{l} {}_{9}{C_{0}} - {}_{9}{C_{1}} . 8 + {}_{9}{C_{2}} {(8)}^{2} - {}_{9}{C_{3}} {(8)}^{3} \\ + \dots {}_{9}{C_{9}} {(8)}^{9} \end{array}] \\ = (7 \times 8 + 9 \times 8) + (21 \times 8^{2} - 36 \times 8^{2}) + \dots \\ = (56 + 72) + (21 - 36) \times 8^{2} + \dots \\ = 128 + 64 (21 - 36) + \dots \\ = 64 [2 + (21 - 36) + \dots] \\ w h i c h i s d i v i s i b l e b y 64 . \\ H e n c e, t h e g i v e n s t a t e m e n t i s' T r u e' . \end{array}

Commonly asked questions

The sum of the series ^{10 20} _{r =0} C_ris 2¹⁹ + ²⁰ C₁₀/2

This is a True or False Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} \sum_{r = 0}^{10} {}_{20}{C_{r}} = {}_{20}{C_{0}} + {}_{20}{C_{1}} + {}_{20}{C_{2}} + {}_{20}{C_{3}} + \dots + {}_{20}{C_{10}} \\ = {}_{20}{C_{0}} + {}_{20}{C_{1}} + \dots + {}_{20}{C_{10}} + {}_{20}{C_{11}} + \dots + {}_{20}{C_{20}} - ({}_{20}{C_{11}} + \dots + {}_{20}{C_{20}}) \\ = 2^{20} - ({}_{20}{C_{11}} + \dots + {}_{20}{C_{20}}) \\ H e n c e, t h e g i v e n s t a t e m e n t i s' F a l s e' \end{array}$

The expression $7^{9} + 9^{7}$ is divisible by 64.

[Hint: $7^{9} + 9^{7} = {(1 + 8)}^{9} - {(1 - 8)}^{7}$ .]

This is a True or False Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} 7^{9} + 9^{7} = {(1 + 8)}^{7} - {(1 - 8)}^{9} \\ = [{}_{7}{C_{0}} + {}_{7}{C_{1}} . 8 + {}_{7}{C_{2}} {(8)}^{2} + {}_{7}{C_{3}} {(8)}^{3} + \dots + {}_{7}{C_{7}} {(8)}^{7}] - [\begin{array}{l} {}_{9}{C_{0}} - {}_{9}{C_{1}} . 8 + {}_{9}{C_{2}} {(8)}^{2} - {}_{9}{C_{3}} {(8)}^{3} \\ + \dots {}_{9}{C_{9}} {(8)}^{9} \end{array}] \\ = (7 \times 8 + 9 \times 8) + (21 \times 8^{2} - 36 \times 8^{2}) + \dots \\ = (56 + 72) + (21 - 36) \times 8^{2} + \dots \\ = 128 + 64 (21 - 36) + \dots \\ = 64 [2 + (21 - 36) + \dots] \\ w h i c h i s d i v i s i b l e b y 64 . \\ H e n c e, t h e g i v e n s t a t e m e n t i s' T r u e' . \end{array}$

The number of terms in the expansion of ${[{(2 x + y^{3})}^{4}]}^{7}$ is 8.

This is a True or False Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} G i v e n expression i s {[{(2 x + y^{3})}^{4}]}^{7} = {(2 x + y^{3})}^{28} \\ H e r e, n = 28 \\ ∴ T h e n u m b e r o f t e r m s i n g i v e n expression i s (n + 1) \\ i . e ., 28 + 1 = 29 \\ H e n c e, t h e g i v e n s t a t e m e n t i s' F a l s e' . \end{array}$

The sum of coefficients of the two middle terms in the expansion of ${(1 + x)}^{2 n - 1}$ is equal to ${}_{2 n - 1}{C_{n}}$ .

This is a True or False Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} G i v e n expression i s {(1 + x)}^{2 n - 1} \\ N u m b e r o f t e r m s = 2 n - 1 + 1 = 2 n (e v e n) \\ ∴ M i d d l e t e r m s a r e \frac{2 n}{2} t h t e r m a n d {(\frac{2 n}{2} + 1)}^{t h} t e r m s = n t h t e r m s a n d (n + 1) t h t e r m s \\ C o e f f i c i e n t o f n t h t e r m = {}_{2 n - 1}{C_{n - 1}} \\ a n d t h e c o e f f i c i e n t o f (n + 1) t h t e r m = {}_{2 n - 1}{C_{n}} \\ S u m o f t h e c o e f f i c i e n t s = {}_{2 n - 1}{C_{n - 1}} + {}_{2 n - 1}{C_{n}} \\ = {}_{2 n - 1 + 1}{C_{n}} = {}_{2 n}{C_{n}} [? {}_{n}{C_{r}} + {}_{n}{C_{r - 1}} = {}_{n + 1}{C_{r}}] \\ H e n c e, t h e g i v e n s t a t e m e n t i s' F a l s e' . \end{array}$

The last two digits of the number $3^{400}$ are 01.

This is a True or False Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} G i v e n t h a t 3^{400} = {(9)}^{200} = {(10 - 1)}^{200} \\ ∴ {(10 - 1)}^{200} = {}_{200}{C_{0}} {(10)}^{200} + {}_{200}{C_{1}} {(10)}^{199} + \dots - {}_{200}{C_{199}} {(10)}^{1} + {}_{200}{C_{200}} {(1)}^{200} \\ = 1 0^{200} - 200 \times 1 0^{199} + \dots - 10 \times 200 + 1 \\ S o, i t i s c l e a r t h a t l a s t t w o d i g i t s a r e 01 . \\ H e n c e, t h e g i v e n s t a t e m e n t i s' T r u e' . \end{array}$

If the expansion of ${(x - \frac{1}{x^{2}})}^{2 n}$ contains a term independent of $x$ , then $n$ is a multiple of 2.

This is a True or False Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} G i v e n expression i s {(x - \frac{1}{x^{2}})}^{2 n} \\ T_{r + 1} = {}_{2 n}{C_{r}} {(x)}^{2 n - r} {(- \frac{1}{x^{2}})}^{r} = {}_{2 n}{C_{r}} {(x)}^{2 n - r} {(- 1)}^{r} . \frac{1}{x^{2 r}} \\ = {}_{2 n}{C_{r}} {(x)}^{2 n - r - 2 r} {(- 1)}^{r} = {}_{2 n}{C_{r}} {(x)}^{2 n - 3 r} {(- 1)}^{r} \\ F o r t h e t e r m i n d e p e n d e n t o f x, 2 n - 3 r = 0 \\ ∴ r = \frac{2 n}{3} w h i c h i s n o t a n integer a n d t h e expression i s n o t p o s s i b l e t o b e t r u e . \\ H e n c e, t h e g i v e n s t a t e m e n t i s' F a l s e' . \end{array}$

The number of terms in the expansion of ${(a + b)}^{n}$ where $n \in ℕ$ is one less than the power $n$ .

This is a True or False Type Questions as classified in NCERT Exemplar
Sol:

$\begin{array}{l} Since, t h e n u m b e r o f t e r m s i n t h e g i v e n expression i s {(a + b)}^{n} i s 1 m o r e t h a n n i . e ., n + 1 \\ H e n c e, t h e g i v e n s t a t e m e n t i s' F a l s e' . \end{array}$

JEE Mains

Maths NCERT Exemplar Solutions Class 11th Chapter Eight Exam

Student Forum

Anything you would want to ask experts?

Write here...

Other Similar chapters for you

Binomial Theorem

News & Updates

Latest NewsPopular News

Maths NCERT Exemplar Solutions Class 11th Chapter Eight: Overview, Questions, Preparation

Binomial Theorem Long Answer Type Questions

Commonly asked questions

Binomial Theorem Short Answer Type Questions

Commonly asked questions

Binomial Theorem Objective Type Questions

Commonly asked questions

Binomial Theorem Fill in the Blanks

Commonly asked questions

Binomial Theorem True or False Type Questions

Commonly asked questions

JEE Mains

Student Forum

Other Similar chapters for you

News & Updates

TS SSC Exam Time table 2026 Soon @bse.telangana.gov.in; Live Updates on Telangana SSC Board Exam Dates

HP Board Date Sheet 10th, 12th Class 2026 @hpbose.org Live Updates; Check HPBOSE Exam Dates Shortly Here

JEE Main 2026 Application Form Live: Form Correction Dates OUT; NTA Registration Last Date Nov 27

CMAT 2026 Registration Last Date Live Updates; Apply Online @cmat.nta.nic.in

JEE Main Marks vs Percentile vs Rank 2025: Calculate Percentile and Rank Using Marks

List of NIT Colleges in India 2025 - NIRF Ranking, Courses, Seats, Cutoff, Fees and Placement

CBSE 10th Maths Question Paper 2025, 2024, 2023, 2022, 2020, 2019 PDF Download

NEET Chapter Wise Weightage 2026 PDF by NTA: Physics, Chemistry & Biology

Last 5 Years Question Papers of SSC Maharashtra Board PDF Download