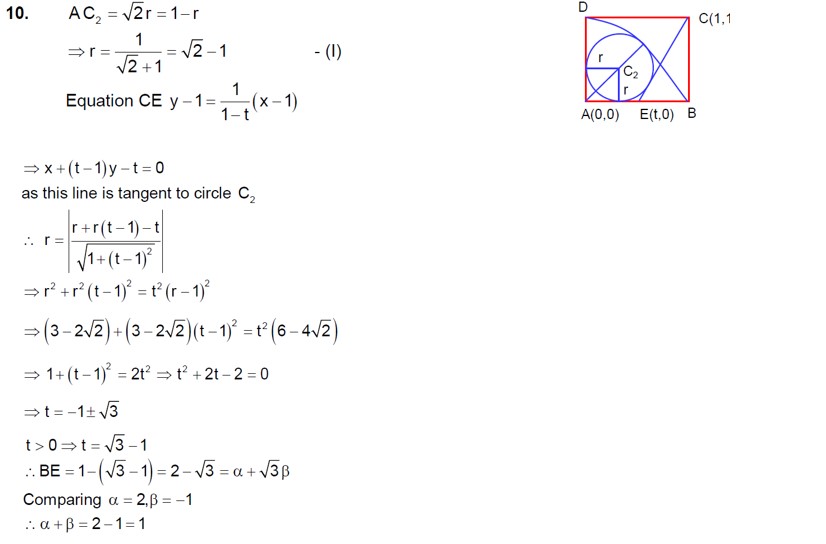- Permutations and Combinations Short Answer Type Questions
- Permutations and Combinations Long Answer Type Questions
- Permutations and Combinations Objective Type Questions
- Permutations and Combinations Fill in the Blanks Type Questions
- Permutations and Combinations True or False Type Questions
- Permutations and Combinations Matching Type Questions
Permutations and Combinations Short Answer Type Questions
| 1. Eight chairs are numbered 1 to 8. Two women and 3 men wish to occupy one chair each. First the women choose the chairs from amongst the chairs 1 to 4 and then men select from the remaining chairs. Find the total number of possible arrangements. [Hint: 2 women occupy the chair, from 1 to 4 in 4P2 ways and 3 men occupy the remaining chairs in 6P3 ways.] |
| Sol. |
| 2. If the letters of the word RACHIT are arranged in all possible ways as listed in dictionary, then what is the rank of the word RACHIT? |
| Sol. |
Commonly asked questions
Eight chairs are numbered 1 to 8. Two women and 3 men wish to occupy one chair each. First the women choose the chairs from amongst the chairs 1 to 4 and then men select from the remaining chairs. Find the total number of possible arrangements.
[Hint: 2 women occupy the chair, from 1 to 4 in 4P2 ways and 3 men occupy the remaining chairs in 6P3 ways.]
This is a short answer type question as classified in NCERT Exemplar
If the letters of the word RACHIT are arranged in all possible ways as listed in dictionary, then what is the rank of the word RACHIT?
[Hint: In each case number of words beginning with A, C, H, I is 5!]
This is a short answer type question as classified in NCERT Exemplar
A candidate is required to answer 7 questions out of 12 questions, which are divided into two groups, each containing 6 questions. He is not permitted to attempt more than 5 questions from either group. Find the number of different ways of doing questions.
This is a short answer type question as classified in NCERT Exemplar
Out of 18 points in a plane, no three are in the same line except five points which are collinear. Find the number of lines that can be formed joining the points.
[Hint: Number of straight lines = 18C2 – 5C2 + 1.]
This is a long answer type question as classified in NCERT Exemplar
We wish to select 6 persons from 8, but if the person A is chosen, then B must be chosen. In how many ways can selections be made?
This is a long answer type question as classified in NCERT Exemplar
How many committees of five persons with a chairperson can be selected from 12 persons?
This is a long answer type question as classified in NCERT Exemplar
How many automobile license plates can be made if each plate contains two different letters followed by three different digits?
This is a long answer type question as classified in NCERT Exemplar
A box contains two white, three black and four red balls. In how many ways can three balls be drawn from the box, if at least one black ball is to be included in the draw?
[Hint: Required number of ways = 3C1 × 6C2 + 3C2 × 6C2 + 3C3.]
This is a short answer type question as classified in NCERT Exemplar
A bag contains 5 black and 6 red balls. Determine the number of ways in which 2 black and 3 red balls can be selected from the lot.
This is a long answer type question as classified in NCERT Exemplar
Find the number of permutations of n distinct things taken r together, in which 3 particular things must occur together.
This is a long answer type question as classified in NCERT Exemplar
Find the number of different words that can be formed from the letters of the word ‘TRIANGLE’ so that no vowels are together.
This is a long answer type question as classified in NCERT Exemplar
Find the number of positive integers greater than 6000 and less than 7000 which are divisible by 5, provided that no digit is to be repeated.
This is a short answer type question as classified in NCERT Exemplar
There are 10 persons named P1, P2, P3, ... P10. Out of 10 persons, 5 persons are to be arranged in a line such that in each arrangement P1 must occur whereas P4 and P5 do not occur. Find the number of such possible arrangements.
[Hint: Required number of arrangement = 7C4 × 5!]
This is a short answer type question as classified in NCERT Exemplar
There are 10 lamps in a hall. Each one of them can be switched on independently. Find the number of ways in which the hall can be illuminated.
[Hint: Required number = 210 – 1.]
This is a short answer type question as classified in NCERT Exemplar
If nCr – 1 = 36, nCr = 84, and nCr + 1 = 126, then find rC2.
[Hint: Form equation using C(n, r-1), C(n, r), and C(n, r+1) to find the value of r.]
This is a short answer type question as classified in NCERT Exemplar
Find the number of integers greater than 7000 that can be formed with the digits 3, 5, 7, 8, and 9 where no digits are repeated.
[Hint: Besides 4-digit integers greater than 7000, five-digit integers are always greater than 7000.]
This is a short answer type question as classified in NCERT Exemplar
If 20 lines are drawn in a plane such that no two of them are parallel and no three are concurrent, in how many points will they intersect each other?
This is a short answer type question as classified in NCERT Exemplar
In a certain city, all telephone numbers have six digits, the first two digits always being 41 or 42 or 46 or 62 or 64. How many telephone numbers have all six digits distinct?
This is a short answer type question as classified in NCERT Exemplar
In an examination, a student has to answer 4 questions out of 5 questions; questions 1 and 2 are however compulsory. Determine the number of ways in which the student can make the choice.
This is a short answer type question as classified in NCERT Exemplar
A convex polygon has 44 diagonals. Find the number of its sides.
[Hint: Polygon of n sides has (nC2 – n) number of diagonals.]
This is a short answer type question as classified in NCERT Exemplar
If the normal to the curve y(x) = ∫(from 2 to x) (2t² - 15t + 10)dt at a point (a, b) is parallel to the line x + 3y = -5, a > 1, then the value of |a + 6b| is equal to..........
y (x) = ∫? (2t² - 15t + 10)dt
dy/dx = 2x² - 15x + 10.
For tangent at (a, b), slope is m = dx/dy = 1 / (dy/dx) = 1 / (2a² - 15a + 10).
Given slope is -1/3.
2a² - 15a + 10 = -3
2a² - 15a + 13 = 0 (The provided solution has 2a²-15a+7=0, suggesting a different problem or a typo)
Following the image: 2a² - 15a + 7 = 0
(2a - 1) (a - 7) = 0
a = 1/2 or a = 7.
a = 1/2 Rejected as a > 1. So a = 7.
b = ∫? (2t² - 15t + 10)dt = [2t³/3 - 15t²/2 + 10t] from 0 to 7.
6b = [4t³ - 45t² + 60t] from 0 to 7 = 4 (7)³ - 45 (7)² + 60 (7) = 1372 - 2205 + 420 = -413.
|a + 6b| = |7 - 413| = |-406| = 406.
Let f: R → R be a continuous function such that f(x) + f(x + 1) = 2, for all x ∈ R. If I? = ∫(from 0 to 8) f(x)dx and I? = ∫(from -1 to 3) f(x)dx, then the value of I? + 2I? is equal to.........
f (x) + f (x + 1) = 2 (1)
replace x with x + 1: f (x + 1) + f (x + 2) = 2 (2)
(2) - (1) ⇒ f (x + 2) = f (x)
∴ f (x) is periodic with period 2.
I? = ∫? f (x)dx = 4 ∫? ² f (x)dx.
I? = ∫? ³ f (x)dx = ∫? f (u-1)du. Let u = x+1.
I? = ∫? f (x-1)dx = 2 ∫? ² f (x-1)dx.
From (1), f (x-1) + f (x) = 2.
I? + 2I? = 4∫? ² f (x)dx + 2 (2∫? ² f (x-1)dx) = 4∫? ² f (x)dx + 4∫? ² (2 - f (x)dx
= 4∫? ² (f (x) + 2 - f (x)dx = 4∫? ² 2 dx = 4 [2x] from 0 to 2 = 16.
Let the curve y = y(x) be the solution of the differential equation, dy/dx = 2(x + 1). If the numerical value of area bounded by the curve y = y(x) and x-axis is 4√8/3, then the value of y(1) is equal to........
Let z and ω be two complex numbers such that ω = zz? - 2z + 2, |(z + i)/(z - 3i)| = 1 and Re(ω) has minimum value. Then, the minimum value of n ∈ N for which ω? is real, is equal to
|z+i|/|z-3i| = 1 ⇒ |z+i| = |z-3i|. This means z is on the perpendicular bisector of the segment from -i to 3i. The midpoint is i, so z = x+i.
w = z? - 2z + 2. Let z = x + iy.
w = (x² + y²) - 2 (x + iy) + 2 = (x² - 2x + 2 + y²) - 2iy.
Re (w) = x² - 2x + 2 + y² = (x - 1)² + 1 + y².
From the first condition, y=1. Re (w) = (x - 1)² + 1 + 1 = (x - 1)² + 2.
Re (w) is minimum for x = 1.
The common z is z = 1 + i.
w = (1+i) (1-i) - 2 (1+i) + 2 = 2 - 2 - 2i + 2 = 2 - 2i.
w² = (2 - 2i)² = 4 (1 - 2i - 1) = -8i.
w? = (-8i)² = -64 ∈ R.
∴ least n ∈ N for which w? ∈ R is n=4.
If lim (x→0) (ae? - bcosx + ce??)/(xsinx) = 2, then a+b+c is equal to........
lim (x→0) [a e? - b cos (x) + c e? ] / (x sin (x) = 2
Using Taylor expansions around x=0:
lim (x→0) [a (1+x+x²/2!+.) - b (1-x²/2!+.) + c (1-x+x²/2!+.)] / (x * x) = 2
lim (x→0) [ (a-b+c) + x (a-c) + x² (a/2+b/2+c/2) + O (x³)] / x² = 2
For the limit to exist, the coefficients of lower powers of x in the numerator must be zero.
a - b + c = 0
a - c = 0 ⇒ a = c
Substituting a=c into the first equation: 2a - b = 0 ⇒ b = 2a.
The limit becomes: lim (x→0) [x² (a/2 + b/2 + c/2)] / x² = (a+b+c)/2
(a + b + c) / 2 = 2 ⇒ a + b + c = 4.
Let f: (0, 2) → R be defined as f(x) = log?(1 + tan(πx/4)). Then, lim (n→∞) (2/n) [f(1/n) + f(2/n) + .... + f(1)] is equal to.......
A = lim (n→∞) (2/n) ∑ (r=1 to n) f (r/n + n/ (n²)
(The term n/n² seems intended to be part of the function argument, not simply added. The solution proceeds as if it's f (r/n)
A = lim (n→∞) (2/n) ∑ (r=1 to n) [ f (r/n) + f (1/n) + . + f (n-1)/n) ]
The expression in the image seems to be: A = lim (n→∞) (2/n) [ f (1/n) + f (2/n) + . + f (n-1)/n) ]
A = 2 ∫? ¹ f (x) dx = 2 ∫? ¹ log? (1 + tan (πx/4) dx
put πx/4 = t ⇒ dx = 4/π dt
A = 2 ∫? ^ (π/4) log? (1 + tan (t) * (4/π) dt = (8/π) ∫? ^ (π/4) log? (1 + tan (t) dt
Using the property ∫? f (x)dx = ∫? f (a-x)dx, the integral ∫? ^ (π/4) log (1 + tan (t)dt evaluates to (π/8)ln (2).
A = (8/π) * (π/8)ln (2) / ln (2) = 1.
The total number of 3 x 3 matrices A having entries from the set {0,1,2,3} such that the sum of all the diagonal entries of AA? is 9, is equal to........
Let A = [a? ]? Sum of diagonal elements of A.A? is Tr (A.A? ) = ∑? ∑? a? ² = 9.
where each a? ∈ {0, 1, 2, 3}.
Case I: One of a? = 3 and rest are 0. (3²=9). There are? C? = 9 ways.
Case II: Two of a? are 2, one is 1, and rest are 0. (2² + 2² + 1² = 9). There are? C? *? C? = 36 * 7 = 252 ways.
Case III: One of a? = 2, five are 1, and rest are 0. (2² + 1²+1²+1²+1²+1² = 9). There are? C? *? C? = 9 * 56 = 504 ways.
Case IV: All nine a? = 1. (1² * 9 = 9). There is 1 way.
Total = 9 + 252 + 504 + 1 = 766.
Let P = [[-30, 20, 56],,] and A = [[2, 7, ω²], [-1, -ω, 1], [0, -ω, -ω+1]] where ω = (-1 + i√3)/2, and I be the identity matrix of order 3. If the determinant of the matrix (P?¹AP - I)² is αω², then the value of α is equal to.........
(P? ¹AP - I)²
= (P? ¹AP - I) (P? ¹AP - I)
= P? ¹A (PP? ¹)AP - P? ¹AP - P? ¹AP + I
= P? ¹A²P - 2P? ¹AP + I
= P? ¹ (A² - 2A + I)P = P? ¹ (A - I)²P
| (P? ¹AP - I)²| = |P? ¹ (A - I)²P| = |P? ¹| | (A - I)²| |P| = | (A - I)²| = |A - I|²
A - I = [1, 7, w²], [-1, w², 1], [0, -w, -w]
|A - I| = 1 (-w³ + w) - 7 (w) + w² (w) = -w³ + w - 7w + w³ = -6w.
|A - I|² = (-6w)² = 36w².
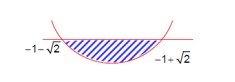
Let ABCD be a square of side of unit length. Let a circle C? centered at A with unit radius is drawn. Another circle C? which touches C? and the lines AD and AB are tangent to it, is also drawn. Let a tangent line from the point C to the circle C? meet the side AB at E. if the length of EB is α + √3β, where α, β are integers, then α + β is equal to.......... + √3β, where α, β are integers, then α + β is equal to..........
Kindly consider the following Image
Let the lines y + 2x = and be normal to a circle C : If the line is tangent to the circle C, then the value of is equal to……………..
………(i)
………(ii)
………(iii)
Centre of the circle given by solving (i) & (ii)
Again is tangent to the circle.
Permutations and Combinations Long Answer Type Questions
| 1. 18 mice were placed in two experimental groups and one control group, with all groups equally large. In how many ways can the mice be placed into three groups? |
| Sol. |
| 2. A bag contains six white marbles and five red marbles. Find the number of ways in which four marbles can be drawn from the bag if: (i) They can be of any colour. (ii) Two must be white and two red. (iii) They must all be of the same colour. |
| Sol. |
Commonly asked questions
18 mice were placed in two experimental groups and one control group, with all groups equally large. In how many ways can the mice be placed into three groups?
This is a long answer type question as classified in NCERT Exemplar
A bag contains six white marbles and five red marbles. Find the number of ways in which four marbles can be drawn from the bag if:
(i) They can be of any colour.
(ii) Two must be white and two red.
(iii) They must all be of the same colour.
This is a long answer type question as classified in NCERT Exemplar
In how many ways can a football team of 11 players be selected from 16 players? How many of them will:
(i) Include 2 particular players?
(ii) Exclude 2 particular players?
This is a long answer type question as classified in NCERT Exemplar
A sports team of 11 students is to be constituted, choosing at least 5 from Class XI and at least 5 from Class XII. If there are 20 students in each of these classes, in how many ways can the team be constituted?
This is a long answer type question as classified in NCERT Exemplar
A group consists of 4 girls and 7 boys. In how many ways can a team of 5 members be selected if the team has:
(i) No girls.
(ii) At least one boy and one girl.
(iii) At least three girls.
This is a long answer type question as classified in NCERT Exemplar
Permutations and Combinations Objective Type Questions
| 1. If nC12 = nC8, then n is equal to: (a) 20 (b) 12 (c) 6 (d) 30 |
| Sol. |
| 2.The number of possible outcomes when a coin is tossed 6 times is: (a) 36 (b) 64 (c) 12 (d) 32 |
| Sol. |
Commonly asked questions
The total number of 9-digit numbers which have all different digits is:
(a) 10!
(b) 9!
(c) 9 × 9!
(d) 10 × 10!
This is an Objective Type Questions as classified in NCERT Exemplar
The number of words that can be formed out of the letters of the word "ARTICLE" so that vowels occupy the even places is:
(a) 1440
(b) 144
(c) 7!
(d) 4C4 × 3C3
This is an Objective Type Questions as classified in NCERT Exemplar
Given 5 different green dyes, four different blue dyes, and three different red dyes, the number of combinations of dyes that can be chosen, taking at least one green and one blue dye, is:
(a) 3600
(b) 3720
(c) 3800
(d) 3600
[Hint: Possible numbers of choosing or not choosing 5 green dyes, 4 blue dyes, and 3 red dyes are , respectively.]
This is an Objective Type Questions as classified in NCERT Exemplar
If nC12 = nC8, then n is equal to:
(a) 20
(b) 12
(c) 6
(d) 30
This is an Objective Type Questions as classified in NCERT Exemplar
The number of possible outcomes when a coin is tossed 6 times is:
(a) 36
(b) 64
(c) 12
(d) 32
This is an Objective Type Questions as classified in NCERT Exemplar
The number of different four-digit numbers that can be formed with the digits 2, 3, 4, 7 and using each digit only once is:
(a) 120
(b) 96
(c) 24
(d) 100
This is an Objective Type Questions as classified in NCERT Exemplar
The sum of the digits in the unit place of all the numbers formed with the help of 3, 4, 5, and 6 taken all at a time is:
(a) 432
(b) 108
(c) 36
(d) 18
This is an Objective Type Questions as classified in NCERT Exemplar
The total number of words formed by 2 vowels and 3 consonants taken from 4 vowels and 5 consonants is equal to:
(a) 60
(b) 120
(c) 7200
(d) 720
This is an Objective Type Questions as classified in NCERT Exemplar
A five-digit number divisible by 3 is to be formed using the numbers 0, 1, 2, 3, 4, and 5 without repetitions. The total number of ways this can be done is:
(a) 216
(b) 600
(c) 240
(d) 3125
[Hint: 5-digit numbers can be formed using digits 0, 1, 2, 4, 5 or by using digits 1, 2, 3, 4, 5 since the sum of digits in these cases is divisible by 3.]
This is an Objective Type Questions as classified in NCERT Exemplar
Everybody in a room shakes hands with everybody else. The total number of handshakes is 66. The total number of persons in the room is:
(a) 11
(b) 12
(c) 13
(d) 14
This is an Objective Type Questions as classified in NCERT Exemplar
The number of triangles that are formed by choosing the vertices from a set of 12 points, seven of which lie on the same line, is:
(a) 105
(b) 15
(c) 75
(d) 185
This is an Objective Type Questions as classified in NCERT Exemplar
The number of parallelograms that can be formed from a set of four parallel lines intersecting another set of three parallel lines is:
(a) 6
(b) 18
(c) 12
(d) 9
This is an Objective Type Questions as classified in NCERT Exemplar
The number of ways in which a team of eleven players can be selected from 22 players always including 2 of them and excluding 4 of them is:
(a) 16C11
(b) 16C5
(c) 16C9
(d) 20C9
This is an Objective Type Questions as classified in NCERT Exemplar
The number of 5-digit telephone numbers having at least one of their digits repeated is:
(a) 90,000
(b) 10,000
(c) 30,240
(d) 69,760
This is an Objective Type Questions as classified in NCERT Exemplar
The number of ways in which we can choose a committee from four men and six women so that the committee includes at least two men and exactly twice as many women as men is:
(a) 94
(b) 126
(c) 128
(d) None
This is an Objective Type Questions as classified in NCERT Exemplar
Permutations and Combinations Fill in the Blanks Type Questions
| 1. If npr = 840, nCr = 35, then ______. |
| Sol. |
| 2.15C8 + 15C9 – 15C6 – 15C7 = ______. |
| Sol. |
Commonly asked questions
If npr = 840, nCr = 35, then ______.
This is an Objective Type Questions as classified in NCERT Exemplar
15C8 + 15C9 – 15C6 – 15C7 = ______.
This is an Objective Type Questions as classified in NCERT Exemplar
The number of permutations of different objects, taken at a time, when repetitions are allowed, is ______.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
The number of different words that can be formed from the letters of the word INTERMEDIATE such that two vowels never come together is ______.
[Hint: Number of ways of arranging 6 consonants of which two are alike is and number of ways of arranging vowels .]
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
Three balls are drawn from a bag containing 5 red, 4 white, and 3 black balls. The number of ways in which this can be done if at least 2 are red is ______.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
The number of six-digit numbers, all digits of which are odd, is ______.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
In a football championship, 153 matches were played. Every two teams played one match with each other. The number of teams participating in the championship is ______.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
The total number of ways in which six ‘+’ and four ‘–’ signs can be arranged in a line such that no two signs ‘–’ occur together is ______.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
A committee of 6 is to be chosen from 10 men and 7 women so as to contain at least 3 men and 2 women. In how many different ways can this be done if two particular women refuse to serve on the same committee?
[Hint: At least 3 men and 2 women: The number of ways = 10C3 × 10C3 + 10C4 × 7C2. For 2 particular women to be always there: the number of ways = 10C4 × 10C3 × 5C1. The total number of committees when two particular women are never together = Total – together.]
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
A box contains 2 white balls, 3 black balls, and 4 red balls. The number of ways three balls can be drawn from the box if at least one black ball is to be included in the draw is ______.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
Permutations and Combinations True or False Type Questions
| 1. There are 12 points in a plane of which 5 points are collinear, then the number of lines obtained by joining these points in pairs is 12C2 - 5C2. |
| Sol. |
| 2. Three letters can be posted in five letterboxes in 35 ways. |
| Sol. |
Commonly asked questions
Eighteen guests are to be seated, half on each side of a long table. Four particular guests desire to sit on one particular side and three others on the other side of the table. The number of ways in which the seating arrangements can be made is .
This is a True or False Type Questions as classified in NCERT Exemplar
There are 12 points in a plane of which 5 points are collinear, then the number of lines obtained by joining these points in pairs is 12C2 - 5C2.
This is a True or False Type Questions as classified in NCERT Exemplar
In the permutations of things, taken together, the number of permutations in which particular things occur together is .
This is a True or False Type Questions as classified in NCERT Exemplar
In a steamer, there are stalls for 12 animals, and there are horses, cows, and calves (not less than 12 each) ready to be shipped. They can be loaded in 312 ways.
This is a True or False Type Questions as classified in NCERT Exemplar
Three letters can be posted in five letterboxes in 35 ways.
This is a True or False Type Questions as classified in NCERT Exemplar
If some or all of objects are taken at a time, the number of combinations is .
This is a True or False Type Questions as classified in NCERT Exemplar
There will be only 24 selections containing at least one red ball out of a bag containing 4 red and 5 black balls. It is given that the balls of the same colour are identical.
This is a True or False Type Questions as classified in NCERT Exemplar
A candidate is required to answer 7 questions out of 12 questions which are divided into two groups, each containing 6 questions. He is not permitted to attempt more than 5 questions from either group. He can choose the seven questions in 650 ways.
This is a True or False Type Questions as classified in NCERT Exemplar
To fill 12 vacancies there are 25 candidates, of which 5 are from scheduled castes. If 3 of the vacancies are reserved for scheduled caste candidates while the rest are open to all, the number of ways in which the selection can be made is 5C3 × 20.
This is a True or False Type Questions as classified in NCERT Exemplar
Permutations and Combinations Matching Type Questions
| 1. There are 3 books on Mathematics, 4 on Physics, and 5 on English. How many different collections can be made such that each collection consists of: C1 | C2 (a) One book of each subject; | (i) 3968 (b) At least one book of each subject: | (ii) 60 (c) At least one book of English: | (iii) 3255 |
| Sol. |
| 2.Five boys and five girls form a line. Find the number of ways of making the seating arrangement under the following condition C1 | C2 (a) Boys and girls alternate: | (i) 5! × 6! (b) No two girls sit together: | (ii) 10! – 5! 6! (c) All the girls sit together: | (iii) (5!)² + (5!)² (d) All the girls are never together: | (iv) 2! 5! 5! |
| Sol. |
Commonly asked questions
Five boys and five girls form a line. Find the number of ways of making the seating arrangement under the following condition
C1 | C2
(a) Boys and girls alternate: | (i) 5! × 6!
(b) No two girls sit together: | (ii) 10! – 5! 6!
(c) All the girls sit together: | (iii) (5!)² + (5!)²
(d) All the girls are never together: | (iv) 2! 5! 5!
This is a matching answer type question as classified in NCERT Exemplar
There are 10 professors and 20 lecturers, out of whom a committee of 2 professors and 3 lecturers is to be formed. Find:
C1 | C2
(a) In how many ways can the committee be formed: | (i) 10C2 × 19C3
(b) In how many ways a particular professor is included: | (ii) 10C2 × 19C2
(c) In how many ways a particular lecturer is included: | (iii) 9C1 × 20C3
(d) In how many ways a particular lecturer is excluded: | (iv) 10C2 × 20C3
This is a matching answer type question as classified in NCERT Exemplar
How many words (with or without dictionary meaning) can be made from the letters of the word MONDAY, assuming that no letter is repeated, if
C1 | C2
(a) 4 letters are used at a time | (i) 720
(b) All letters are used at a time | (ii) 240
(c) All letters are used but the first is a vowel | (iii) 360
This is a matching answer type question as classified in NCERT Exemplar
There are 3 books on Mathematics, 4 on Physics, and 5 on English. How many different collections can be made such that each collection consists of:
C1 | C2
(a) One book of each subject; | (i) 3968
(b) At least one book of each subject: | (ii) 60
(c) At least one book of English: | (iii) 3255
This is a matching answer type question as classified in NCERT Exemplar
Using the digits 1, 2, 3, 4, 5, 6, 7, a number of 4 different digits is formed. Find:
C1 C2
(a) How many numbers are formed? | (i) 840
(b) How many numbers are exactly divisible by 2? | (ii) 200
(c) How many numbers are exactly divisible by 25? | (iii) 360
(d) How many of these are exactly divisible by 4? | (iv) 40
This is a matching answer type question as classified in NCERT Exemplar
Maths NCERT Exemplar Solutions Class 11th Chapter Seven Exam