A sample space consists of 9 elementary outcomes e 1 , e 2 , … , e 9 whose probabilities are: P ( e 1 ) = P ( e 2 ) = 0 . 0 8 , P ( e 3 ) = P ( e 4 ) = P ( e 5 ) = 0 . 1 , P ( e 6 ) = P ( e 7 ) = 0 . 2 , P ( e 8 ) = P ( e 9 ) = 0 . 0 7 . Suppose A = { e 1 , e 5 , e 8 } , B = { e 2 , e 5 , e 8 , e 9 } . (a) Calculate P ( A ) , P ( B ) , and P ( A ∩ B ) . (b) Using the addition law of probability, calculate P ( A ∪ B ) . (c) List the composition of the event A ∪ B , and calculate P ( A ∪ B ) by adding the probabilities of the elementary outcomes. (d) Calculate P ( B ′ ) from P ( B ) , also calculate P ( B ′ ) directly from the elementary outcomes of B .

This is a long answer type question as classified in NCERT Exemplar G i v e n t h a t : S = { e 1 , e 2 , e 3 , e 4 , e 5 , e 6 , e 7 , e 8 , e 9 } A = { e 1 , e 5 , e 5 } a n d B = { e 2 , e 5 , e 5 , e 9 } P ( e 1 ) = P ( e 2 ) = 0 . 0 8 P ( e 3 ) = P ( e 4 ) = P ( e 5 ) = 0 . 1 P ( e 6 ) = P ( e 7 ) = 0 . 2 P ( e 8 ) = P ( e 9 ) = 0 . 0 7 ( a ) P ( A ) = P ( e 1 ) + P ( e 5 ) + P ( e 8 ) = 0 . 0 8 + 0 . 1 + 0 . 0 7 = 0 . 2 5 ( b ) P ( A ∪ B ) = P ( A ) + P ( B ) − P ( A ∩ B ) … ( i ) B u t P ( B ) = P ( e 2 ) + P ( e 5 ) + P ( e 8 ) + P ( e 9 ) = 0 . 0 8 + 0 . 1 + 0 . 0 7 + 0 . 0 7 = 0 . 3 2 a n d P ( A ∩ B ) = { e 5 , e 8 } = P ( e 5 ) + P ( e 8 ) = 0 . 1 + 0 . 0 7 = 0 . 1 7 P u t t i n g t h e v a l u e s i n e q n . ( i ) w e g e t P ( A ∪ B ) = 0 . 2 5 + 0 . 3 2 − 0 . 1 7 = 0 . 4 0 ( c ) P ( A ∪ B ) = { e 1 , e 2 , e 5 , e 8 , e 9 } ∴ P ( A ∪ B ) = P ( e 1 ) + P ( e 2 ) + P ( e 5 ) + P ( e 8 ) + P ( e 9 ) = 0 . 0 8 + 0 . 0 8 + 0 . 1 + 0 . 0 7 + 0 . 0 7 = 0 . 4 0 ( d ) &t

Maths NCERT Exemplar Solutions Class 11th Chapter Sixteen: Overview, Questions, Preparation

Updated on Sep 8, 2025 14:16 IST

By Payal Gupta, Retainer

Table of contents

Probability Short Answer Type Questions
Probability Long Answer Type Questions
Probability Objective Type Questions
Probability True or False Type Questions
Probability Fill in the blank Type Questions
Probability Matching Type Questions

Probability Short Answer Type Questions

1. If the letters of the word ALGORITHM are arranged at random in a row, what is the probability that the letters GOR must remain together as a unit?

Sol.

\begin{array}{l} W o r d A L G O R I T H M h a s 9 l e t t e r s . \\ I f G O R r e m a i n t o g e t h e r, t h e n i t w i l l r e m a i n t o g e t h e r . \\ ∴ N u m b e r o f l e t t e r s = A L G O R I T H M = 6 + 1 = 7 \\ N u m b e r o f w o r d s = 7! \\ a n d t h e t o t a l n u m b e r o f w o r d s f r o m A L G O R I T H M = 9! \\ S o, t h e r e q u i r e d p r o b a b i l i t y = \frac{7!}{9!} = \frac{7!}{9.8.7!} = \frac{1}{72} \\ H e n c e, t h e r e q u i r e d p r o b a b i l i t y = \frac{1}{72} . \end{array}

2. Six new employees, two of whom are married to each other, are to be assigned six desks that are lined up in a row. If the assignment of employees to desks is made randomly, what is the probability that the married couple will have nonadjacent desks?

[Hint: First find the probability that the couple has adjacent desks, and then subtract it from 1.]

Sol.

\begin{array}{l} W o r d A L G O R I T H M h a s 9 l e t t e r s . \\ N u m b e r o f d e s k o c c u p i e d b y o n e c o u p l e = 1 \\ O n l y (4 + 1) = 5 p e r s o n s t o b e a s s i g n e d . \\ ∴ N u m b e r o f w a y s o f a s s i g n i n g t h e s e 5 p e r s o n s = 5! \times 2! \\ T o t a l n u m b e r o f w a y s o f a s s i g n i n g t h e s e 6 p e r s o n s = 6! \\ ∴ Probability t h a t a c o u p l e h a s a d j a c e n t d e s k = \frac{5! \times 2!}{6!} = \frac{1}{3} \\ S o, t h e p r o b a b i l i t y t h a t t h e m a r r i e d c o u p l e w i l l h a v e n o - a d j a c e n t d e s k s = 1 - \frac{1}{3} = \frac{2}{3} \\ H e n c e, t h e r e q u i r e d p r o b a b i l i t y = \frac{2}{3} . \end{array}

Commonly asked questions

Six new employees, two of whom are married to each other, are to be assigned six desks that are lined up in a row. If the assignment of employees to desks is made randomly, what is the probability that the married couple will have nonadjacent desks?

[Hint: First find the probability that the couple has adjacent desks, and then subtract it from 1.]

This is a short answer type question as classified in NCERT Exemplar $\begin{array}{l} W o r d A L G O R I T H M h a s 9 l e t t e r s . \\ N u m b e r o f d e s k o c c u p i e d b y o n e c o u p l e = 1 \\ O n l y (4 + 1) = 5 p e r s o n s t o b e a s s i g n e d . \\ ∴ N u m b e r o f w a y s o f a s s i g n i n g t h e s e 5 p e r s o n s = 5! \times 2! \\ T o t a l n u m b e r o f w a y s o f a s s i g n i n g t h e s e 6 p e r s o n s = 6! \\ ∴ Probability t h a t a c o u p l e h a s a d j a c e n t d e s k = \frac{5! \times 2!}{6!} = \frac{1}{3} \\ S o, t h e p r o b a b i l i t y t h a t t h e m a r r i e d c o u p l e w i l l h a v e n o a d j a c e n t d e s k s = 1 - \frac{1}{3} = \frac{2}{3} \\ H e n c e, t h e r e q u i r e d p r o b a b i l i t y = \frac{2}{3} . \end{array}$

If the letters of the word ALGORITHM are arranged at random in a row, what is the probability that the letters GOR must remain together as a unit?

This is a short answer type question as classified in NCERT Exemplar

$\begin{array}{l} W o r d A L G O R I T H M h a s 9 l e t t e r s . \\ I f G O R r e m a i n t o g e t h e r, t h e n i t w i l l r e m a i n t o g e t h e r . \\ ∴ N u m b e r o f l e t t e r s = A L G O R I T H M = 6 + 1 = 7 \\ N u m b e r o f w o r d s = 7! \\ a n d t h e t o t a l n u m b e r o f w o r d s f r o m A L G O R I T H M = 9! \\ S o, t h e r e q u i r e d p r o b a b i l i t y = \frac{7!}{9!} = \frac{7!}{9.8.7!} = \frac{1}{72} \\ H e n c e, t h e r e q u i r e d p r o b a b i l i t y = \frac{1}{72} . \end{array}$

Suppose an integer from 1 through 1000 is chosen at random. Find the probability that the integer is a multiple of 2 or a multiple of 9.

This is a short answer type question as classified in NCERT Exemplar

$\begin{array}{l} W e h a v e m u l t i p l e s o f 2, f r o m 1 t o 1000 a r e 2, 4, 6, 8, \dots, 1000 \\ L e t n b e t h e n u m b e r o f t e r m s \\ H e r e a = 2, d = 2, a_{n} = 1000 \\ a_{n} = a + (n - 1) d \\ 1000 = 2 + (n - 1) 2 \\ \Rightarrow 1000 = 2 n \Rightarrow n = 500 \\ N o w m u l t i p l e s o f 9, f r o m 1 t o 1000 a r e 9, 18, 27, \dots, 999 \\ H e r e a = 9, d = 9, a_{m} = 999 [m b e t h e n u m b e r o f t e r m s] \\ a_{m} = a + (m - 1) d \\ \Rightarrow 999 = 9 + (m - 1) 9 \\ \Rightarrow 999 = 9 m \Rightarrow m = 111 \\ N o w m u l t i p l e s o f 2 a n d 9 a r e 18, 36, 54, \dots, 990 \\ H e r e a = 18, d = 18, a_{p} = 999 [p b e t h e n u m b e r o f t e r m s] \\ ∴ a_{p} = a + (p - 1) d \\ \Rightarrow 990 = 18 + (p - 1) 18 \\ \Rightarrow 990 = 18 p \Rightarrow p = 55 \\ ∴ N u m b e r o f m u l t i p l e s o f 2 o r 9 = 500 + 111 - 55 = 556 \\ ∴ R e q u i r e d p r o b a b i l i t y = \frac{P (E)}{n (E)} = \frac{556}{1000} = 0.556 \\ H e n c e, t h e r e q u i r e d p r o b a b i l i t y = 0.556 \end{array}$

An experiment consists of rolling a die until a 2 appears.

(i) How many elements of the sample space correspond to the event that the 2 appears on the $k^{t h}$ roll of the die?

(ii) How many elements of the sample space correspond to the event that the 2 appears not later than the $k^{t h}$ roll of the die?

This is a short answer type question as classified in NCERT Exemplar

$\begin{array}{l} N u m b e r o f S a m p l e s p a c e = 6 \\ (i) G i v e n t h a t 2 a p p e a r s o n t h e k t h r o l l o f t h e d i e . \\ S o f i r s t (k - 1) t h r o l l h a v e 5 o u t c o m e s e a c h a n d k t h r o l l r e s u l t s 2 i . e . o n l y 1 o u t c o m e . \\ ∴ N u m b e r o f e l e m e n t o f s a m p l e s p a c e c o r r e s p o n d t o t h e e v e n t t h a t 2 a p p e a r s o n t h e k t h \\ r o l l o f t h e d i e = 5^{k - 1} . \\ (i i) I n t h i s c a s e, 2 a p p e a r s n o t l a t e r t h a n k t h r o l l o f t h e d i e, t h e n i t i s p o s s i b l e t h a t 2 c o m e s \\ i n f i r s t t h r o w t h e n o u t c o m e s w i l l b e 5 a n d 2 o u t c o m e s i n second t h r o w i . e . 1 o u t c o m e . \\ ∴ P o s s i b l e o u t c o m e = 5 \times 1 = 5 \\ S i m i l a r l y, i f 2 d o e s n o t a p p e a r i n second t h r o w a n d a p p e a r s i n t h i r d t h r o w \\ ∴ P o s s i b l e o u t c o m e = 5 \times 5 \times 1 \\ N o w w e h a v e t h e s e r i e s : \\ = 1 + 5 + 5 \times 5 + 5 \times 5 \times 5 + \dots + 5^{k - 1} \\ = 1 + 5 + 5^{2} + 5^{3} + \dots + 5^{k - 1} \\ = \frac{1 . (r^{k} - 1)}{r - 1} = \frac{5^{k - 1}}{5 - 1} \\ = \frac{5^{k - 1}}{4} \\ H e n c e, t h e r e q u i r e d p r o b a b i l i t y = \frac{5^{k - 1}}{4} . \end{array}$

A die is loaded in such a way that each odd number is twice as likely to occur as each even number. Find $P (G)$ , where $G$ is the event that a number greater than 3 occurs on a single roll of the die.

This is a short answer type question as classified in NCERT Exemplar

$\begin{array}{l} G i v e n t h a t p r o b a b i l i t y o f e v e n n u m b e r s = \frac{1}{2} \times p r o b a b i l i t y o f o d d n u m b e r s \\ \Rightarrow P (O d d) : P (E v e n) = 2 : 1 \\ ∴ P (o d d n u m b e r) = \frac{2}{2 + 1} = \frac{2}{3} \\ a n d P (e v e n n u m b e r) = \frac{1}{2 + 1} = \frac{1}{3} \\ A l s o, g i v e n t h a t, G t h e e v e n t t h a t a n u m b e r g r e a t e r t h a n 3 o c c u r s i n a single t h r o w o f d i e . \\ ∴ T h e p o s s i b l e o u t c o m e a r e 4, 5 a n d 6 o u t o f w h i c h t w o a r e e v e n a n d o n e i s o d d . \\ ∴ R e q u i r e d p r o b a b i l i t y = P (G) \\ = 2 \times P (e v e n) \times P (o d d) \\ = 2 \times \frac{1}{3} \times \frac{2}{3} = \frac{4}{9} \\ H e n c e, t h e r e q u i r e d p r o b a b i l i t y = \frac{4}{9} . \end{array}$

In a large metropolitan area, the probabilities are 0.87, 0.36, 0.30 that a family (randomly chosen for a sample survey) owns a colour television set, a black and white television set, or both kinds of sets. What is the probability that a family owns either any one or both kinds of sets?

This is a short answer type question as classified in NCERT Exemplar

$\begin{array}{l} L e t E_{1} b e t h e e v e n t t h a t a f a m i l y o w n s c o l o u r t e l e v i s i o n s e t . \\ a n d E_{2} b e t h e e v e n t t h a t a f a m i l y o w n s b l a c k a n d w h i t e t e l e v i s i o n s e t . \\ G i v e n t h a t P (E_{1}) = 0.87, P (E_{2}) = 0.36 \\ a n d P (E_{1} \cap E_{2}) = 0.30 \\ ∴ T h e p r o b a b i l i t y t h a t a f a m i l y o w n s e i t h e r c o l o u r o r b l a c k a n d w h i t e t e l e v i s i o n s e t . \\ ∴ P (E_{1} \cup E_{2}) = P (E_{1}) + P (E_{2}) - P (E_{1} \cap E_{2}) \\ = 0.87 + 0.36 - 0.30 = 0.93 \\ H e n c e, t h e r e q u i r e d p r o b a b i l i t y = 0.93 \end{array}$

If $A$ and $B$ are mutually exclusive events, $P (A) = 0.35$ and $P (B) = 0.45$ , find:

(a) $P (A^{'})$

(b) $P (B^{'})$

(c) $P (A \cup B)$

(d) $P (A \cap B)$

(e) $P (A \cap B^{'})$

(f) $P (A^{'} \cap B^{'})$

This is a short answer type question as classified in NCERT Exemplar

$\begin{array}{l} G i v e n t h a t P (A) = 0.35 a n d P (B) = 0.45 \\ Since t h e e v e n t s A a n d B a r e m u t u a l l y e x c l u s i v e t h e n P (A \cap B) = 0 \\ (a) P (A') = 1 - P (A) = 1 - 0.35 = 0.65 \\ (b) P (B') = 1 - P (B) = 1 - 0.45 = 0.55 \\ (c) P (A \cup B) = P (A) + P (B) - P (A \cap B) = 0.35 + 0.45 - 0 = 0.80 \\ (d) P (A \cap B) = 0 [? A a n d B a r e m u t u a l l y e x c l u s i v e e v e n t s] \\ (e) P (A \cap B') = P (A) - P (A \cap B) = 0.35 - 0 = 0.35 \\ (f) P (A' \cap B') = 1 - P (A \cup B) = 1 - 0.80 = 0.20 \end{array}$

A team of medical students doing their internship has to assist during surgeries at a city hospital. The probabilities of surgeries rated as very complex, complex, routine, simple, or very simple are respectively, 0.15, 0.20, 0.31, 0.26, 0.08. Find the probabilities that a particular surgery will be rated:

(a) complex or very complex;

(b) neither very complex nor very simple;

(c) routine or complex;

(d) routine or simple.

This is a short answer type question as classified in NCERT Exemplar

$\begin{array}{l} L e t E_{1}, E_{2}, E_{3}, E_{4} a n d E_{5} b e t h e e v e n t s t h a t t h e s u r g e r i e s a r e r a t e d a s v e r y c o m p l e x, c o m p l e x, \\ r o u t i n e, s i m p l e a n d v e r y s i m p l e r e s p e c t i v e l y . \\ ∴ P (E_{1}) = 0.15, P (E_{2}) = 0.20, P (E_{3}) = 0.31, P (E_{4}) = 0.26 a n d P (E_{5}) = 0.08 \\ (a) P (c o m p l e x a n d v e r y c o m p l e x) = P (E_{1} o r E_{2}) \\ \Rightarrow P (E_{1} \cup E_{2}) = P (E_{1}) + P (E_{2}) - P (E_{1} \cap E_{2}) \\ = 0.15 + 0.20 - 0 \\ = 0.35 [? A l l e v e n t a r e i n d e p e n d e n t] \\ (b) P (n e i t h e r v e r y c o m p l e x n o r v e r y s i m p l e) = P (E_{1}^{'} \cap E_{5}^{'}) \\ = P (E_{1} \cup E_{5})' = 1 - P (E_{1} \cup E_{5}) \\ = 1 - [P (E_{1}) + P (E_{5})] = 1 - [0.15 + 0.08] \\ = 1 - 0.23 = 0.77 \\ (c) P (r o u t i n e o r c o m p l e x) = P (E_{3} o r E_{2}) \\ \Rightarrow P (E_{3} \cup E_{2}) = P (E_{3}) + P (E_{2}) \\ = 0.31 + 0.20 = 0.51 \\ (d) P (r o u t i n e o r s i m p l e) = P (E_{3} o r E_{4}) \\ \Rightarrow P (E_{3} \cup E_{4}) = P (E_{3}) + P (E_{4}) \\ = 0.31 + 0.26 = 0.57 \end{array}$

Four candidates $A, B, C, D$ have applied for the assignment to coach a school cricket team. If $A$ is twice as likely to be selected as $B$ , and $B$ and $C$ are given about the same chance of being selected, while $C$ is twice as likely to be selected as $D$ , what are the probabilities that:

(a) C will be selected?

(b) A will not be selected?

This is a short answer type question as classified in NCERT Exemplar

$\begin{array}{l} G i v e n t h a t A i s t w i c e a s l i k e l y t o b e s e l e c t e d a s B \\ i . e ., P (A) = 2 P (B) \\ a n d C i s t w i c e a s l i k e l y t o b e s e l e c t e d a s D \\ ∴ P (C) = 2 P (D) \Rightarrow P (B) = 2 P (D) \\ \Rightarrow \frac{P (A)}{2} = 2 P (D) \Rightarrow P (D) = \frac{1}{4} P (A) \\ N o w B a n d C a r e g i v e n a b o u t t h e s a m e c h a n c e \\ ∴ P (B) = P (C) \\ Since, s u m o f a l l p r o b a b i l i t i e s = 1 \\ ∴ P (A) + P (B) + P (C) + P (D) = 1 \\ \Rightarrow P (A) + \frac{P (A)}{2} + \frac{P (A)}{2} + \frac{P (A)}{4} = 1 \\ \Rightarrow 4 P (A) + 2 P (A) + 2 P (A) + P (A) = 4 \\ \Rightarrow 9 P (A) = 4 \Rightarrow P (A) = \frac{4}{9} \\ (a) P (C w i l l b e s e l e c t e d) = P (C) = P (B) = \frac{P (A)}{2} \\ = \frac{4}{9} \times \frac{1}{2} = \frac{2}{9} \\ (b) P (A w i l l n o t b e s e l e c t e d) = P (A') = 1 - P (A) \\ &thi \end{array}$

One of the four persons, John, Rita, Aslam, or Gurpreet, will be promoted next month. Consequently, the sample space consists of four elementary outcomes:

S = {John promoted, Rita promoted, Aslam promoted, Gurpreet promoted}

You are told that the chances of John’s promotion are the same as that of Gurpreet. Rita’s chances of promotion are twice as likely as John’s. Aslam’s chances are four times that of John.

(a) Determine P (John promoted),

P (Rita promoted),

P (Aslam promoted), and

P (Gurpreet promoted).

(b) If A = {John promoted or Gurpreet promoted}, find P(A).

This is a short answer type question as classified in NCERT Exemplar

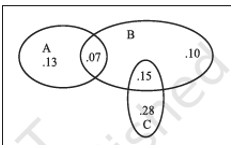
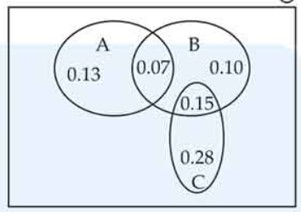
$\begin{array}{l} L e t E_{1}, E_{2}, E_{3} a n d E_{4} b e t h e e v e n t s t h a t J o h n p r o m o t e d, R i t a p r o m o t e d, A s l a m p r o m o t e d \\ a n d G u r p r e e t p r o m o t e d r e s p e c t i v e l y . \\ ∴ S a m p l e s p a c e S = {E_{1}, E_{2}, E_{3}, E_{4}} \\ G i v e n t h a t p r o b a b i l i t y o f J o h n' s p r o m o t i o n i s s a m e a s t h a t o f G u r p r e e t \\ ∴ P (E_{1}) = P (E_{4}) \\ R i t a' s c h a n c e s o f p r o m o t i o n a r e t w i c e a s l i k e l y a s J o h n \\ ∴ P (E_{2}) = 2 P (E_{1}) \\ A n d A s l a m' s c h a n c e s o f p r o m o t i o n a r e 4 t i m e s t h a t o f J o h n \\ ∴ P (E_{3}) = 4 P (E_{1}) \\ Since, t h e s u m o f a l l p r o b a b i l i t i e s = 1 \\ ∴ P (E_{1}) + P (E_{2}) + P (E_{3}) + P (E_{4}) = 1 \\ \Rightarrow P (E_{1}) + 2 P (E_{1}) + 4 P (E_{1}) + P (E_{1}) = 1 \\ \Rightarrow 8 P (E_{1}) = 1 \\ \Rightarrow P (E_{1}) = \frac{1}{8} \\ (a) P (J o h n p r o m o t e d) = P (E_{1}) = \frac{1}{8} \\ P (R i t a p r o m o t e d) = P (E_{2}) = 2 P (E_{1}) = 2 \times \frac{1}{8} = \frac{2}{8} \\ P (A s l a m p r o m o t e d) = P (E_{3}) = 4 P (E_{1}) = 4 \times \frac{1}{8} = \frac{4}{8} = \frac{1}{2} \\ P (G u r p r e e t p r o m o t e d) = P (E_{4}) = P (E_{1}) = \frac{1}{8} \\ (b) P (J o h n p r o m o t e d o r G u r p r e e t p r o m o t e d) = P (E_{1} \cup E_{4}) \\ \Rightarrow &th \end{array}$

The accompanying Venn diagram shows three events, A, B, and C, and also the probabilities of the various intersections (for instance, P (A ∩ B) = .07). Determine

(a) P (A)

(b) P (B ∩ C )

(d) P (A ∩ B )

(e) P (B ∩ C)

(f) Probability of exactly one of the three occurs.

This is a short answer type question as classified in NCERT Exemplar

$\begin{array}{l} F r o m t h e g i v e n V e n n d i a g r a m \\ (a) P (A) = 0.13 + 0.07 = 0.20 \\ (b) P (B \cap \bar{C}) = P (B) - P (B \cap C) \\ = 0.07 + 0.10 + 0.15 - 0.15 = 0.07 + 0.10 = 0.17 \\ (c) P (A \cup B) = P (A) + P (B) - P (A \cap B) \\ = 0.13 + 0.07 + 0.07 + 0.10 + 0.15 - 0.07 \\ = 0.13 + 0.07 + 0.10 + 0.15 = 0.45 \\ (d) P (A \cap \bar{B}) = P (A) - P (A \cap B) \\ = 0.13 + 0.07 - 0.07 = 0.13 \\ (e) P (B \cap C) = 0.15 \\ (f) P (e x a c t l y o n e o f t h e t h r e e o c c u r s) = 0.13 + 0.10 + 0.28 = 0.51 \end{array}$

Probability Long Answer Type Questions

1. One urn contains two black balls (labeled $B_{1}$ and $B_{1}$ ) and one white ball. A second urn contains one black ball and two white balls (labeled $W_{1}$ and $W_{2}$ ). Suppose the following experiment is performed: one of the two urns is chosen at random. Next, a ball is randomly chosen from the urn. Then a second ball is chosen at random from the same urn without replacing the first ball.

(a) Write the sample space showing all possible outcomes.

(b) What is the probability that two black balls are chosen?

(c) What is the probability that two balls of opposite color are chosen?

Sol.

\begin{array}{l} G i v e n t h a t o n e o f t h e u r n s i s c h o o s e n, t h e n a b a l l i s r a n d o m l y c h o o s e n f r o m t h e u r n, t h e n \\ a second b a l l i s c h o o s e n a t r a n d o m f r o m t h e s a m e u r n w i t h o u t r e p l a c i n g t h e f i r s t b a l l \\ (a) S a m p l e s p a c e S = {B_{1} B_{2}, B_{1} W, B_{2} B_{1}, B_{2} W, W B_{1}, W B_{2}, B W_{1}, B W_{2}, W_{1} B, W_{1} W_{2}, W_{2} B, W_{2} W_{1}} \\ T o t a l n u m b e r o f S a m p l e s p a c e, S = 12 \\ (b) I f t w o b l a c k b a l l s a r e c h o o s e n \\ t h e n t h e f a v o u r a b l e e v e n t s a r e B_{1} B_{2}, B_{2} B_{1} i . e . 2 \\ ∴ R e q u i r e d p r o b a b i l i t y = \frac{2}{12} = \frac{1}{6} \\ (c) I f t w o b a l l s o f o p p o s i t e c o l o u r s a r e c h o o s e n t h e n, t h e \\ r e q u i r e d p r o b a b i l i t y = \frac{8}{12} = \frac{2}{3} \end{array}

2. A bag contains 8 red and 5 white balls. Three balls are drawn at random. Find the probability that:

(a) All the three balls are white.

(b) All the three balls are red.

(c) One ball is red and two balls are white.

Sol.

\begin{array}{l} G i v e n t h a t : N u m b e r o f r e d b a l l s = 8 \\ N u m b e r o f w h i t e b a l l s = 5 \\ (a) P (a l l t h e t h r e e b a l l s a r e w h i t e) \\ = \frac{{}_{5}{C_{3}}}{{}_{13}{C_{3}}} = \frac{\frac{5!}{3! 2!}}{\frac{13!}{3! 10!}} = \frac{5!}{3! 2!} \times \frac{3! 10!}{13!} \\ = \frac{5!}{2!} \times \frac{10!}{13 \times 12 \times 11 \times 10!} \\ = \frac{5 \times 4 \times 3 \times 2!}{2!} \times \frac{1}{13 \times 12 \times 11} = \frac{5 \times 4 \times 3}{13 \times 12 \times 11} = \frac{5}{143} \\ (b) P (a l l t h e t h r e e b a l l s a r e r e d) \\ = \frac{{}_{8}{C_{3}}}{{}_{13}{C_{3}}} = \frac{\frac{8!}{3! 5!}}{\frac{13!}{3! 10!}} = \frac{8!}{3! 5!} \times \frac{3! 10!}{13!} \\ = \frac{8 \times 7 \times 6 \times 5!}{5!} \times \frac{10!}{13 \times 12 \times 11 \times 10!} \\ = \frac{8 \times 7 \times 6}{13 \times 12 \times 11} = \frac{28}{143} \\ (c) P (o n e b a l l i s r e d a n d t w o b a l l s a r e w h i t e) \\ = \frac{{}_{8}{C_{1}} \times {}_{5}{C_{2}}}{{}_{13}{C_{3}}} = \frac{\frac{8!}{7! 1!} \times \frac{5!}{2! 3!}}{\frac{13!}{3! 10!}} = \frac{8 \times 7!}{7!} \times \frac{5 \times 4 \times 3 \times 2!}{2! \times 3!} \times \frac{3! \times 10!}{13 \times 12 \times 11 \times 10!} \\ = \frac{8 \times 5}{13 \times 11} = \frac{40}{143} \end{array}

Commonly asked questions

One urn contains two black balls (labeled $B_{1}$ and $B_{1}$ ) and one white ball. A second urn contains one black ball and two white balls (labeled $W_{1}$ and $W_{2}$ ). Suppose the following experiment is performed: one of the two urns is chosen at random. Next, a ball is randomly chosen from the urn. Then a second ball is chosen at random from the same urn without replacing the first ball.

(a) Write the sample space showing all possible outcomes.

(b) What is the probability that two black balls are chosen?

(c) What is the probability that two balls of opposite color are chosen?

This is a long answer type question as classified in NCERT Exemplar

$\begin{array}{l} G i v e n t h a t o n e o f t h e u r n s i s c h o o s e n, t h e n a b a l l i s r a n d o m l y c h o o s e n f r o m t h e u r n, t h e n \\ a second b a l l i s c h o o s e n a t r a n d o m f r o m t h e s a m e u r n w i t h o u t r e p l a c i n g t h e f i r s t b a l l \\ (a) S a m p l e s p a c e S = {B_{1} B_{2}, B_{1} W, B_{2} B_{1}, B_{2} W, W B_{1}, W B_{2}, B W_{1}, B W_{2}, W_{1} B, W_{1} W_{2}, W_{2} B, W_{2} W_{1}} \\ T o t a l n u m b e r o f S a m p l e s p a c e, S = 12 \\ (b) I f t w o b l a c k b a l l s a r e c h o o s e n \\ t h e n t h e f a v o u r a b l e e v e n t s a r e B_{1} B_{2}, B_{2} B_{1} i . e . 2 \\ ∴ R e q u i r e d p r o b a b i l i t y = \frac{2}{12} = \frac{1}{6} \\ (c) I f t w o b a l l s o f o p p o s i t e c o l o u r s a r e c h o o s e n t h e n, t h e \\ r e q u i r e d p r o b a b i l i t y = \frac{8}{12} = \frac{2}{3} \end{array}$

A bag contains 8 red and 5 white balls. Three balls are drawn at random. Find the probability that:

(a) All the three balls are white.

(b) All the three balls are red.

(c) One ball is red and two balls are white.

This is a long answer type question as classified in NCERT Exemplar

$\begin{array}{l} G i v e n t h a t : N u m b e r o f r e d b a l l s = 8 \\ N u m b e r o f w h i t e b a l l s = 5 \\ (a) P (a l l t h e t h r e e b a l l s a r e w h i t e) \\ = \frac{{}_{5}{C_{3}}}{{}_{13}{C_{3}}} = \frac{\frac{5!}{3! 2!}}{\frac{13!}{3! 10!}} = \frac{5!}{3! 2!} \times \frac{3! 10!}{13!} \\ = \frac{5!}{2!} \times \frac{10!}{13 \times 12 \times 11 \times 10!} \\ = \frac{5 \times 4 \times 3 \times 2!}{2!} \times \frac{1}{13 \times 12 \times 11} = \frac{5 \times 4 \times 3}{13 \times 12 \times 11} = \frac{5}{143} \\ (b) P (a l l t h e t h r e e b a l l s a r e r e d) \\ = \frac{{}_{8}{C_{3}}}{{}_{13}{C_{3}}} = \frac{\frac{8!}{3! 5!}}{\frac{13!}{3! 10!}} = \frac{8!}{3! 5!} \times \frac{3! 10!}{13!} \\ = \frac{8 \times 7 \times 6 \times 5!}{5!} \times \frac{10!}{13 \times 12 \times 11 \times 10!} \\ = \frac{8 \times 7 \times 6}{13 \times 12 \times 11} = \frac{28}{143} \\ (c) P (o n e b a l l i s r e d a n d t w o b a l l s a r e w h i t e) \\ = \frac{{}_{8}{C_{1}} \times {}_{5}{C_{2}}}{{}_{13}{C_{3}}} = \frac{\frac{8!}{7! 1!} \times \frac{5!}{2! 3!}}{\frac{13!}{3! 10!}} = \frac{8 \times 7!}{7!} \times \frac{5 \times 4 \times 3 \times 2!}{2! \times 3!} \times \frac{3! \times 10!}{13 \times 12 \times 11 \times 10!} \\ = \frac{8 \times 5}{13 \times 11} = \frac{40}{143} \end{array}$

If the letters of the word ASSASSINATION are arranged at random, find the probability that:

(a) Four S’s come consecutively in the word.

(b) Two I’s and two N’s come together.

(c) All A’s are not coming together.

(d) No two A’s are coming together.

This is a long answer type question as classified in NCERT Exemplar

$\begin{array}{l} T o t a l n u m b e r o f w o r d i s A S S A S S I N A T I O N a r e 13 . \\ W h e r e, w e h a v e 3 A' s, 4 S' s, 2 I' s, 2 N' s, 1 T' s a n d 1 O' s . \\ (a) I f 4 S' s c o m e consecutively i n t h e w o r d, t h e n a r r a n g e m e n t m a y b e a s f o l l o w s : \\ \underset{1 G r o u p}{S S S S} \underset{9 o t h e r s}{\underset{?}{A A A I I N N T O}} \\ ∴ N u m b e r o f w o r d s w h e n a l l S' s a r e t o g e t h e r = \frac{10!}{3! 2! 2!} \end{array}$

$\begin{array}{l} a n d t h e t o t a l n u m b e r o f w o r d f o r m e d f r o m t h e w o r d s A S S A S S I N A T I O N = \frac{13!}{3! 4! 2! 2!} \\ ∴ R e q u i r e d p r o b a b i l i t y = \frac{\frac{10!}{3! 2! 2!}}{\frac{13!}{3! 4! 2! 2!}} = \frac{10!}{3! 2! 2!} \times \frac{3! 4! 2! 2!}{13!} \\ = \frac{10! 4!}{13!} = \frac{10! \times 4 \times 3 \times 2}{13 \times 12 \times 11 \times 10!} = \frac{2}{143} \\ (b) I f 2 I' s a n d 2 N' s c o m e t o g e t h e r t h e n t h e r e a r e 10 a l p h a b e t s \\ N u m b e r o f w o r d s w h e n 2 I' s a n d 2 N' s c o m e t o g e t h e r = \frac{10!}{3! 4!} \times \frac{4!}{2! 2!} \\ ∴ R e q u i r e d p r o b a b i l i t y = \frac{\frac{10!}{3! 4!} \times \frac{4!}{2! 2!}}{\frac{13!}{3! 4! 2! 2!}} = \frac{10!}{3! 4!} \times \frac{4!}{2! 2!} \times \frac{3! 4! 2! 2!}{13!} \\ = \frac{4! 10!}{13!} = \frac{4 \times 3 \times 2 \times 10!}{13 \times 12 \times 11 \times 10!} = \frac{2}{143} \\ (c) I f a l l A' s a r e coming t o g e t h e r, t h e n t h e r e a r e 11 a l p h a b e t s \\ N u m b e r o f w o r d s w h e n a l l A' s c o m e t o g e t h e r = \frac{11!}{4! 2! 2!} \\ ∴ P r o b a b i l i t y w h e n a l l A' s c o m e t o g e t h e r = \frac{\frac{11!}{4! 2! 2!}}{\frac{13!}{4! 3! 2! 2!}} = \frac{11!}{4! 2! 2!} \times \frac{4! 3! 2! 2!}{13!} \\ = \frac{11! 3!}{13!} = \frac{6}{13 \times 12} = \frac{1}{26} \\ ∴ R e q u i r e d p r o b a b i l i t y w h e n a l l A' s d o n o t c o m e t o g e t h e r = 1 - \frac{1}{26} = \frac{25}{26} \\ (d) I f n o t w o A' s a r e t o g e t h e r, t h e n a r r a n g i n g t h e a l p h a b e t s e x c e p t A' s \\ - S - S - S - S - I - N - T - I - O - N - \\ N u m b e r o f w a y s o f a r r a n g i n g a l l a l p h a b e t s e x c e p t A' s = \frac{10!}{4! 2! 2!} \\ T h e r e a r e 11 v a c a n t p l a c e s b e t w e e n t h e s e a l p h a b e t s . \\ ∴ 3 A' s c a n b e p l a c e d i n 11 p l a c e s i n {}_{11}{C_{3}} w a y s = \frac{11!}{3! 8!} \\ ∴ T o t a l n u m b e r o f w o r d s w h e n n o t w o A' s c o m e t o g e t h e r = \frac{11!}{3! 8!} \times \frac{10!}{4! 2! 2!} \\ ∴ R e q u i r e d p r o b a b i l i t y = \frac{11!}{3! 8!} \times \frac{10!}{4! 2! 2!} \times \frac{4! 3! 2! 2!}{13!} \\ = \frac{10!}{8! \times 13 \times 12} = \frac{10 \times 9 \times 8!}{8! \times 13 \times 12} = \frac{10 \times 9}{13 \times 12} = \frac{15}{26} \end{array}$

A card is drawn from a deck of 52 cards. Find the probability of getting a king or a heart or a red card.

This is a long answer type question as classified in NCERT Exemplar

$\begin{array}{l} T o t a l n u m b e r o f c a r d s = 52 \\ F a v o u r a b l e e v e n t s = 4 k i n g s + 13 h e a r t s + 26 r e d - 13 - 2 = 28 \\ ∴ R e q u i r e d p r o b a b i l i t y = \frac{28}{52} = \frac{7}{13} . \end{array}$

A sample space consists of 9 elementary outcomes $e_{1}, e_{2}, \dots, e_{9}$ whose probabilities are:

$P (e_{1}) = P (e_{2}) = 0.08$ , $P (e_{3}) = P (e_{4}) = P (e_{5}) = 0.1$ , $P (e_{6}) = P (e_{7}) = 0.2$ , $P (e_{8}) = P (e_{9}) = 0.07$ .

Suppose $A = {e_{1}, e_{5}, e_{8}}$ , $B = {e_{2}, e_{5}, e_{8}, e_{9}}$ .

(a) Calculate $P (A)$ , $P (B)$ , and $P (A \cap B)$ .

(b) Using the addition law of probability, calculate $P (A \cup B)$ .

(c) List the composition of the event $A \cup B$ , and calculate $P (A \cup B)$ by adding the probabilities of the elementary outcomes.

(d) Calculate $P (B^{'})$ from $P (B)$ , also calculate $P (B^{'})$ directly from the elementary outcomes of $B$ .

This is a long answer type question as classified in NCERT Exemplar

$\begin{array}{l} G i v e n t h a t : S = {e_{1}, e_{2}, e_{3}, e_{4}, e_{5}, e_{6}, e_{7}, e_{8}, e_{9}} \\ A = {e_{1}, e_{5}, e_{5}} a n d B = {e_{2}, e_{5}, e_{5}, e_{9}} \\ P (e_{1}) = P (e_{2}) = 0.08 \\ P (e_{3}) = P (e_{4}) = P (e_{5}) = 0.1 \\ P (e_{6}) = P (e_{7}) = 0.2 \\ P (e_{8}) = P (e_{9}) = 0.07 \\ (a) P (A) = P (e_{1}) + P (e_{5}) + P (e_{8}) \\ = 0.08 + 0.1 + 0.07 = 0.25 \\ (b) P (A \cup B) = P (A) + P (B) - P (A \cap B) \dots (i) \\ B u t P (B) = P (e_{2}) + P (e_{5}) + P (e_{8}) + P (e_{9}) \\ = 0.08 + 0.1 + 0.07 + 0.07 = 0.32 \\ a n d P (A \cap B) = {e_{5}, e_{8}} = P (e_{5}) + P (e_{8}) \\ = 0.1 + 0.07 = 0.17 \\ P u t t i n g t h e v a l u e s i n e q n . (i) w e g e t \\ P (A \cup B) = 0.25 + 0.32 - 0.17 = 0.40 \\ (c) P (A \cup B) = {e_{1}, e_{2}, e_{5}, e_{8}, e_{9}} \\ ∴ P (A \cup B) = P (e_{1}) + P (e_{2}) + P (e_{5}) + P (e_{8}) + P (e_{9}) \\ = 0.08 + 0.08 + 0.1 + 0.07 + 0.07 = 0.40 \\ (d) &t \end{array}$

Determine the probability p, for each of the following events.

(a) An odd number appears in a single toss of a fair die.

(b) At least one head appears in two tosses of a fair coin.

(c) A king, 9 of hearts, or 3 of spades appears in drawing a single card from a well shuffled ordinary deck of 52 cards.

(d) The sum of 6 appears in a single toss of a pair of fair dice.

This is a long answer type question as classified in NCERT Exemplar

$\begin{array}{l} (a) P o s s i b l e o u t c o m e o f a single t h r o w o f d i e \\ S = {1, 2, 3, 4, 5, 6} o u t o f w h i c h 1, 3, 5 a r e o d d \\ ∴ R e q u i r e d p r o b a b i l i t y = \frac{3}{6} = \frac{1}{2} \\ (b) W h e n a f a i r c o i n i s t o s s e d t w i c e, t h e n t h e s a m p l e s p a c e \\ S = {H H, H T, T H, T T} \\ ∴ P r o b a b i l i t y o f g e t t i n g a t l e a s t o n e h e a d (H H, H T, T H) = \frac{3}{4} \\ (c) F a v o u r a b l e e v e n t s a r e 4 k i n g s + 2 o f h e a r t s + 3 o f s p a d e s = 4 + 1 + 1 = 6 = \frac{6}{52} = \frac{3}{26} \\ (d) W h e n a p a i r o f d i c e i s r o l l e d, t h e n t o t a l n u m b e r o f s a m p l e s p a c e = 36 o u t o f w h i c h \\ (1, 5), (5, 1), (2, 4), (4, 2) a n d (3, 3) a r e t h e f a v o u r a b l e e v e n t s \\ ∴ R e q u i r e d p r o b a b i l i t y = \frac{5}{36} . \end{array}$

Probability Objective Type Questions

1. In a non-leap year, the probability of having 53 Tuesdays or 53 Wednesdays is:

(a) $\frac{1}{7}$

(b) $\frac{2}{7}$

(c) $\frac{3}{7}$

(d) None of these

Sol.

\begin{array}{l} T h e r e a r e 365 d a y s i n a l e a p y e a r a n d t h e r e a r e 7 d a y s i n a w e e k . \\ ∴ 365 \div 7 = 52 w e e k s + 1 d a y \\ S o, t h i s d a y m a y b e T u e s d a y o r W e d n e s d a y . \\ S o, t h e r e q u i r e d p r o b a b i l i t y = \frac{1}{7} . \\ H e n c e, t h e c o r r e c t o p t i o n i s (a) . \end{array}

2. Three numbers are chosen from 1 to 20. Find the probability that they are not consecutive:

(a) $\frac{186}{190}$

(b) $\frac{187}{190}$

(c) $\frac{188}{190}$

(d) 18/²⁰C₃

Sol.

\begin{array}{l} S e t o f t h r e e c o n s e c u t i v e n u m b e r s f r o m 1 t o 20 a r e 1, 2, 3; 2, 3, 4; 3, 4, 5; \dots; 18, 19, 20 . \\ S o, t h e p r o b a b i l i t y t h a t t h e n u m b e r s a r e consecutive \\ = \frac{18}{{}_{20}{C_{3}}} = \frac{18}{\frac{20!}{3! 7!}} = \frac{18.3! 7!}{20!} \\ = \frac{18 \times 3 \times 2 \times 17!}{20 \times 19 \times 18 \times 17!} = \frac{3 \times 2}{20 \times 19} = \frac{3}{190} \\ ∴ P (t h r e e n u m b e r s a r e n o t consecutive) = 1 - \frac{3}{190} = \frac{187}{190} \\ H e n c e, t h e c o r r e c t o p t i o n i s (b) . \end{array}

Commonly asked questions

A single letter is selected at random from the word “PROBABILITY.” The probability that it is a vowel is:

(a) $\frac{1}{3}$

(b) $\frac{1}{4}$

(c) $\frac{2}{11}$

(d) None of these.

This is an Objective Type Questions as classified in NCERT Exemplar

$\begin{array}{l} T o t a l n u m b e r o f a l p h a b e t s i n p r o b a b i l i t y = 11 \\ N u m b e r o f v o w e l s = 4 \\ ∴ Required p r o b a b i l i t y = \frac{4}{11} \\ H e n c e, t h e c o r r e c t o p t i o n i s (b) . \end{array}$

In a non-leap year, the probability of having 53 Tuesdays or 53 Wednesdays is:

(a) $\frac{1}{7}$

(b) $\frac{2}{7}$

(c) $\frac{3}{7}$

(d) None of these

This is an Objective Type Questions as classified in NCERT Exemplar

$\begin{array}{l} T h e r e a r e 365 d a y s i n a l e a p y e a r a n d t h e r e a r e 7 d a y s i n a w e e k . \\ ∴ 365 \div 7 = 52 w e e k s + 1 d a y \\ S o, t h i s d a y m a y b e T u e s d a y o r W e d n e s d a y . \\ S o, t h e r e q u i r e d p r o b a b i l i t y = \frac{1}{7} . \\ H e n c e, t h e c o r r e c t o p t i o n i s (a) . \end{array}$

Three numbers are chosen from 1 to 20. Find the probability that they are not consecutive:

(a) $\frac{186}{190}$

(b) $\frac{187}{190}$

(c) $\frac{188}{190}$

(d) 18/²⁰C₃

This is an Objective Type Questions as classified in NCERT Exemplar

$\begin{array}{l} S e t o f t h r e e c o n s e c u t i v e n u m b e r s f r o m 1 t o 20 a r e 1, 2, 3; 2, 3, 4; 3, 4, 5; \dots; 18, 19, 20 . \\ S o, t h e p r o b a b i l i t y t h a t t h e n u m b e r s a r e consecutive \\ = \frac{18}{{}_{20}{C_{3}}} = \frac{18}{\frac{20!}{3! 7!}} = \frac{18.3! 7!}{20!} \\ = \frac{18 \times 3 \times 2 \times 17!}{20 \times 19 \times 18 \times 17!} = \frac{3 \times 2}{20 \times 19} = \frac{3}{190} \\ ∴ P (t h r e e n u m b e r s a r e n o t consecutive) = 1 - \frac{3}{190} = \frac{187}{190} \\ H e n c e, t h e c o r r e c t o p t i o n i s (b) . \end{array}$

While shuffling a pack of 52 playing cards, 2 are accidentally dropped. Find the probability that the missing cards are of different colors

(a) $\frac{29}{52}$

(b) $\frac{1}{2}$

(c) $\frac{26}{51}$

(d) $\frac{27}{51}$

This is an Objective Type Questions as classified in NCERT Exemplar

$\begin{array}{l} W e k n o w t h a t o u t o f 52 p l a y i n g c a r d s 26 a r e o f r e d a n d 26 a r e o f b l a c k c o l o u r . \\ ∴ P (b o t h c a r d s o f d i f f e r e n t c o l o u r) = \frac{26}{52} \times \frac{26}{51} + \frac{26}{52} \times \frac{26}{51} \\ = 2 \times \frac{26}{52} \times \frac{26}{51} = \frac{26}{51} \\ H e n c e, t h e c o r r e c t o p t i o n i s (c) . \end{array}$

Seven persons are to be seated in a row. The probability that two particular persons sit next to each other is:

(a) $\frac{1}{3}$

(b) $\frac{1}{6}$

(c) $\frac{2}{7}$

(d) $\frac{1}{2}$

This is an Objective Type Questions as classified in NCERT Exemplar

$\begin{array}{l} T h e t w o p a r t i c u l a r p e r s o n s t o b e s e a t e d n e x t e a c h o t h e r t h e n, t h e y f o r m o n e g r o u p . \\ N o w t h e p e r m u t a t i o n o f 6 p e r s o n s = 6! \times 2! \\ a n d T o t a l n u m b e r o f p e r m u t a t i o n o f 7 p e r s o n s = 7! \\ ∴ Required p r o b a b i l i t y = \frac{6! \times 2!}{7!} \\ = \frac{6! \times 2}{7 \times 6!} = \frac{2}{7} \\ H e n c e, t h e c o r r e c t o p t i o n i s (c) . \end{array}$

If P(A ∪ B) = P(A ∩ B) for any two events A and B, then:

(a) P(A) = P(B)

(b) P(A) > P(B)

(c) P(A) < P(B)

(d) None of these.

This is an Objective Type Questions as classified in NCERT Exemplar

$\begin{array}{l} G i v e n t h a t : P (A \cup B) = P (A \cap B) \\ \Rightarrow P (A) + P (B) - P (A \cap B) = P (A \cap B) \\ \Rightarrow [P (A) - P (A \cap B)] + [P (B) - P (A \cap B)] = 0 \\ B u t P (A) - P (A \cap B) \geq 0 [? P (A \cap B) \leq P (A) o r P (B)] \dots (i) \\ a n d P (B) - P (A \cap B) \geq 0 \dots (i i) \\ F r o m e q n . (i) a n d (i i) w e g e t \\ P (A) = P (B) \\ H e n c e, t h e c o r r e c t o p t i o n i s (a) . \end{array}$

Six boys and six girls sit in a row at random. The probability that all the girls sit together is:

(a) $\frac{1}{432}$

(b) $\frac{12}{431}$

(c) $\frac{1}{132}$

(d) None of these.

This is an Objective Type Questions as classified in NCERT Exemplar

$\begin{array}{l} I f a l l t h e g i r l s s i t t o g e t h e r, t h e n w e c o n s i d e r i t a s 1 g r o u p \\ ∴ T o t a l n u m b e r o f a r r a n g e m e n t o f 6 + 1 = 7 p e r s o n s i n a r o w = 7! \\ a n d t h e g i r l s a l s o t h e i r p l a c e s w i t h 6! w a y s . \\ ∴ Required p r o b a b i l i t y = \frac{6! 7!}{12!} = \frac{6 \times 5 \times 4 \times 3 \times 2 \times 7!}{12 \times 11 \times 10 \times 9 \times 8 \times 7!} = \frac{1}{132} \\ H e n c e, t h e c o r r e c t o p t i o n i s (c) . \end{array}$

$\begin{array}{l} . \end{array}$

If the probabilities for A to fail in an examination are 0.2 and for B are 0.3, then the probability that either A or B fails is:

(a) > 0.5

(b) 0.5

(c) ≤ 0.5

(d) 0

This is an Objective Type Questions as classified in NCERT Exemplar

$\begin{array}{l} G i v e n t h a t : P (A f a i l s) = 0.2 \\ P (B f a i l s) = 0.3 \\ ∴ P (e i t h e r A o r B f a i l s) \leq P (A f a i l s) + P (B f a i l s) \\ \leq 0.2 + 0.3 \\ \leq 0.5 \\ H e n c e, t h e c o r r e c t o p t i o n i s (c) . \end{array}$

The probability that at least one of the events A and B occurs is 0.6. If A and B occur simultaneously with a probability of 0.2, then P(A) + P(B) is:

(a) 0.4

(b) 0.8

(c) 1.2

(d) 1.6

This is an Objective Type Questions as classified in NCERT Exemplar

$\begin{array}{l} G i v e n t h a t : P (A \cup B) = 0.6 \\ P (A \cap B) = 0.2 \\ ∴ P (A \cup B) = P (A) + P (B) - P (A \cap B) \\ \Rightarrow 0.6 = P (A) + P (B) - 0.2 \\ \Rightarrow P (A) + P (B) = 0.6 + 0.2 = 0.8 \\ a n d 1 - P (\bar{A}) + 1 - P (\bar{B}) = 0.8 \\ \Rightarrow P (\bar{A}) + P (\bar{B}) = 2 - 0.8 = 1.2 \\ H e n c e, t h e c o r r e c t o p t i o n i s (c) . \end{array}$

If M and N are any two events, the probability that at least one of them occurs is:

(a) P(M) + P(N) – 2P(M ∩ N)

(b) P(M) + P(N) – P(M ∩ N)

(c) P(M) + P(N) + P(M ∩ N)

(d) P(M) + P(N) + 2P(M ∩ N)

This is an Objective Type Questions as classified in NCERT Exemplar

$\begin{array}{l} I f M a n d N a r e a n y t w o e v e n t s, t h e n \\ P (M \cup N) = P (M) + P (N) - P (M \cap N) \\ H e n c e, t h e c o r r e c t o p t i o n i s (b) . \end{array}$

Without repetition of the numbers, four-digit numbers are formed with the numbers 0, 2, 3, 5. The probability of such a number divisible by 5 is:

(a) $\frac{1}{5}$

(b) $\frac{4}{5}$

(c) $\frac{1}{30}$

(d) $\frac{5}{9}$

This is an Objective Type Questions as classified in NCERT Exemplar $\begin{array}{l} F o u r d i g i t n u m b e r t h e d i g i t s 0, 2, 3, 5 w i t h o u t r e p e t i t i o n a n d d i v i s i b l e b y 5 w i t h t h e \\ g i v e n c o n d i t i o n i s \\ I f u n i t p l a c e b e f i l l e d w i t h 0 \\ T h e n t h e n u m b e r o f w a y s = 3 \times 2 \times 1 \times 1 = 6 \\ I f u n i t p l a c e b e f i l l e d w i t h 5 \\ T h e n t h e n u m b e r o f w a y s = 2 \times 2 \times 1 \times 1 = 4 \\ ∴ T o t a l n u m b e r o f w a y s = 6 + 4 = 10 \\ T o t a l n u m b e r o f w a y s o f a r r a n g i n g t h e d i g i t s 0, 2, 3, 5 t o f o r m 4 d i g i t n u m b e r s w i t h o u t \\ r e p e t i t i o n i s 3 \times 3 \times 2 \times 1 = 18 \\ ∴ Required p r o b a b i l i t y = \frac{10}{18} = \frac{5}{9} \\ H e n c e, t h e c o r r e c t o p t i o n i s (d) . \end{array}$

If A and B are mutually exclusive events, then: (A) P

(a) ≤ P(B)

(b) P(A) ≥ P(B)

(c) P(A) < P(B)

(d) None of these.

This is an Objective Type Questions as classified in NCERT Exemplar

$\begin{array}{l} F o r m u t u a l l y e x c l u s i v e e v e n t s, \\ P (A \cap B) = 0 \\ ∴ P (A \cup B) = P (A) + P (B) [? P (A \cap B) = 0] \\ \Rightarrow P (A) + P (B) \leq 1 \\ \Rightarrow P (A) + 1 - P (\bar{B}) \leq 1 [? P (B) = 1 - P (\bar{B})] \\ \Rightarrow P (A) - P (\bar{B}) \leq 0 \\ \Rightarrow P (A) \leq P (\bar{B}) \\ H e n c e, t h e c o r r e c t o p t i o n i s (a) . \end{array}$

Probability True or False Type Questions

1. The probability that a person visiting a zoo will see the giraffe is 0.72, the probability that he will see the bears is 0.84, and the probability that he will see both is 0.52.

Sol.

\begin{array}{l} G i v e n t h a t : \\ P (t o s e e g i r a f f e e) = 0.72 \\ P (t o s e e b e a r) = 0.84 \\ P (t o s e e b o t h g i r a f f e e a n d b e a r) = 0.52 \\ ∴ P (t o s e e g i r a f f e e o r b e a r) = P (t o s e e g i r a f f e e) + P (t o s e e b e a r) - P (t o s e e b o t h) \\ = 0.72 + 0.84 - 0.52 \\ = 1.04 w h i c h i s n o t p o s s i b l e . \\ H e n c e, t h e g i v e n s t a t e m e n t i s' F a l s e' . \end{array}

2. The probability that a student will pass his examination is 0.73, the probability of the student getting a compartment is 0.13, and the probability that the student will either pass or get a compartment is 0.96.

Sol.

\begin{array}{l} L e t E b e t h e e v e n t t h a t t h e s t u d e n t w i l l p a s s \\ a n d F b e t h e e v e n t t h a t h e w i l l g e t c o m p a r t m e n t \\ ∴ P (E) = 0.73, P (F) = 0.13 a n d P (E \cup F) = 0.96 \\ ∴ P (E \cup F) = P (E) + P (F) - P (E \cap F) \\ = 0.73 + 0.13 - 0 [∵ P (E \cap F) = 0] \\ = 0.86 \\ B u t P (E \cup F) = 0.96 \\ H e n c e, t h e g i v e n s t a t e m e n t i s' F a l s e' . \end{array}

Commonly asked questions

The probability that a person visiting a zoo will see the giraffe is 0.72, the probability that he will see the bears is 0.84, and the probability that he will see both is 0.52.

This is a True or False Type Questions as classified in NCERT Exemplar

$\begin{array}{l} G i v e n t h a t : \\ P (t o s e e g i r a f f e e) = 0.72 \\ P (t o s e e b e a r) = 0.84 \\ P (t o s e e b o t h g i r a f f e e a n d b e a r) = 0.52 \\ ∴ P (t o s e e g i r a f f e e o r b e a r) = P (t o s e e g i r a f f e e) + P (t o s e e b e a r) - P (t o s e e b o t h) \\ = 0.72 + 0.84 - 0.52 \\ = 1.04 w h i c h i s n o t p o s s i b l e . \\ H e n c e, t h e g i v e n s t a t e m e n t i s' F a l s e' . \end{array}$

The probability that a student will pass his examination is 0.73, the probability of the student getting a compartment is 0.13, and the probability that the student will either pass or get a compartment is 0.96.

This is a True or False Type Questions as classified in NCERT Exemplar

$\begin{array}{l} L e t E b e t h e e v e n t t h a t t h e s t u d e n t w i l l p a s s \\ a n d F b e t h e e v e n t t h a t h e w i l l g e t c o m p a r t m e n t \\ ∴ P (E) = 0.73, P (F) = 0.13 a n d P (E \cup F) = 0.96 \\ ∴ P (E \cup F) = P (E) + P (F) - P (E \cap F) \\ = 0.73 + 0.13 - 0 [? P (E \cap F) = 0] \\ = 0.86 \\ B u t P (E \cup F) = 0.96 \\ H e n c e, t h e g i v e n s t a t e m e n t i s' F a l s e' . \end{array}$

The probabilities that a typist will make 0, 1, 2, 3, 4, or 5 or more mistakes in typing a report are, respectively, 0.12, 0.25, 0.36, 0.14, 0.08, 0.11.

This is a True or False Type Questions as classified in NCERT Exemplar

$\begin{array}{l} S u m o f a l l p r o b a b i l i t i e s = 1 \\ ∴ P (0) + P (1) + P (2) + P (3) + P (4) + P (5) = 0.12 + 0.25 + 0.36 + 0.14 + 0.08 + 0.11 \\ = 1.06 > 1 \\ H e n c e, t h e g i v e n s t a t e m e n t i s' F a l s e' . \end{array}$

If A and B are two candidates seeking admission in an engineering college, the probability that A is selected is 0.5, and the probability that both A and B are selected is at most 0.3. Is it possible that the probability of B getting selected is 0.7?

This is a True or False Type Questions as classified in NCERT Exemplar

$\begin{array}{l} G i v e n t h a t P (A) = 0.5 a n d P (A \cap B) \leq 0.3 \\ N o w P (A) \times P (B) \leq 0.3 \\ \Rightarrow 0.5 \times P (B) \leq 0.3 \\ \Rightarrow P (B) \leq \frac{0.3}{0.5} \\ \Rightarrow P (B) \leq 0.6 \\ H e n c e, t h e g i v e n s t a t e m e n t i s' F a l s e' \end{array}$

The probability of the occurrence of event A is 0.7 and that of the occurrence of event B is 0.3, but the probability of the occurrence of both is 0.4.

This is a True or False Type Questions as classified in NCERT Exemplar

$\begin{array}{l} H e r e, P (A) = 0.7, P (B) = 0.3 \\ ∴ P (A \cap B) = P (A) \times P (B) \\ = 0.7 \times 0.3 = 0.21 \\ B u t t h e g i v e n p r o b a b i l i t y i s 0.4 \\ H e n c e, t h e g i v e n s t a t e m e n t i s' F a l s e' \end{array}$

The probability of the intersection of two events A and B is always less than or equal to the probability of A.

This is a True or False Type Questions as classified in NCERT Exemplar

$\begin{array}{l} H e r e, P (A \cap B) \leq P (A) W h i c h i s a l w a y s t r u e . \\ H e n c e, t h e g i v e n s t a t e m e n t i s' T r u e' \end{array}$

The sum of probabilities of two students getting distinction in their final examinations is 1.2.

This is a True or False Type Questions as classified in NCERT Exemplar

$\begin{array}{l} Since, t h e t w o g i v e n e v e n t s a r e n o t r e l a t e d t o t h e s a m e S a m p l e s p a c e . \\ ∴ T h e s u m o f p r o b a b i l i t i e s o f t w o s t u d e n t s g e t t i n g d i s t i n c t i o n i n t h e i r f i n a l \\ m a y b e 1.2 \\ H e n c e, t h e g i v e n s t a t e m e n t i s' T r u e' \end{array}$

Probability Fill in the blank Type Questions

1. The probability that the home team will win an upcoming football game is 0.77, the probability that it will tie the game is 0.08, and the probability that it will lose the game is ___.

Sol.

\begin{array}{l} P (loosing t h e g a m e) = 1 - (0.77 + 0.08) \\ = 1 - 0.85 = 0.15 \\ H e n c e, t h e v a l u e o f t h e f i l l e r i s 0.15 \end{array}

2. If e₁, e₂, e₃, e₄ are the four elementary outcomes in a sample space and P(e₁) = 0.1, P(e₂) = 0.5, P(e₃) = 0.1, then the probability of e₄ is __.

Sol.

\begin{array}{l} W e k n o w t h a t t h e s u m o f a l l p r o b a b i l i t i e s = 1 \\ ∴ P (e_{1}) + P (e_{2}) + P (e_{3}) + P (e_{4}) = 1 \\ \Rightarrow 0.1 + 0.5 + 0.1 + P (e_{4}) = 1 \\ \Rightarrow 0.7 + P (e_{4}) = 1 \\ \Rightarrow P (e_{4}) = 1 - 0.7 = 0.3 \\ H e n c e, t h e v a l u e o f t h e f i l l e r i s 0.3 \end{array}

Commonly asked questions

The probability that a person visiting a zoo will see the giraffe is 0.72, the probability that he will see the bears is 0.84, and the probability that he will see both is 0.52.

This is a Fill in the blanks Type Questions as classified in NCERT Exemplar

If A and B are two events associated with a random experiment such that P(A) = 0.3, P(B) = 0.2, and P(A ∩ B) = 0.1, then the value of P(A ∩ B') is ___.

This is a Fill in the blanks Type Questions as classified in NCERT Exemplar

$\begin{array}{l} G i v e n t h a t : P (A) = 0.3, P (B) = 0.2 \\ a n d P (A \cap B) = 0.1 \\ ∴ P (A \cap \bar{B}) = P (A) - P (A \cap B) \\ = 0.3 - 0.1 = 0.2 \\ H e n c e, t h e v a l u e o f t h e f i l l e r i s 0.2 \end{array}$

The probability of happening of event A is 0.5, and that of B is 0.3. If A and B are mutually exclusive events, then the probability of neither A nor B is ____.

This is a Fill in the blanks Type Questions as classified in NCERT Exemplar

$\begin{array}{l} G i v e n t h a t : P (A) = 0.5, P (B) = 0.3 \\ a n d P (A \cap B) = 0 [? A a n d B a r e m u t u a l l y e x c l u s i v e e v e n t s] \\ ∴ P (\bar{A} \cap \bar{B}) = P (\bar{A \cup B}) \\ = 1 - P (A \cup B) = 1 - [P (A) + P (B)] \\ = 1 - (0.5 + 0.3) = 1 - 0.8 = 0.2 \\ H e n c e, t h e v a l u e o f t h e f i l l e r i s 0.2 \end{array}$

Let S = {1, 2, 3, 4, 5, 6} and E = {1, 3, 5}. Then E is ___.

This is a Fill in the blanks Type Questions as classified in NCERT Exemplar

$\begin{array}{l} G i v e n t h a t : S = {1, 2, 3, 4, 5, 6} \\ E = {1, 3, 5} \\ ∴ \bar{E} = S - E = {2, 4, 6} \\ H e n c e, t h e v a l u e o f t h e f i l l e r i s {2, 4, 6} . \end{array}$

Probability Matching Type Questions

1. Match the proposed probability under Column C₁ with the appropriate written description under column C₂ :

C₁ C₂

Probability Written Description

(a) 0.95 (i) An incorrect assignment

(b) 0.02 (ii) No chance of happening

(c) – 0.3 (iii) As much chance of happening as not.

(d) 0.5 (iv) Very likely to happen

(e) 0 (v) Very little chance of happening

Sol.

\begin{array}{l} (a) 0.95 = V e r y l i k e l y t o h a p p e n, s o i t i s c l o s e t o 1 . \\ (b) 0.02 = V e r y l i t t l e c h a n c e o f h a p p e n i n g a s t h e p r o b a b i l i t y i s v e r y l o w . \\ (c) - 0.3 = A n i n c o r r e c t a s s i g n m e n t b e c a u s e p r o b a b i l i t y i s n e v e r n e g a t i v e . \\ (d) 0.5 = A s m u c h c h a n c e o f h a p p e n i n g a s n o t b e c a u s e s u m o f c h a n c e s o f h a p p e n i n g \\ a n d n o t h a p p e n i n g i s o n e . \\ (e) 0 = N o c h a n c e o f h a p p e n i n g . \\ H e n c e, (a) \leftrightarrow (i v), (b) \leftrightarrow (v), (c) \leftrightarrow (i), (d) \leftrightarrow (i i i), (e) \leftrightarrow (i i) \end{array}

2. Match the following

(a) If E₁ and E₂ are the two mutually (i) E₁ ∩ E₂ = E₁ exclusive events

(b) If E₁ and E₂ are the mutually (ii) (E₁ – E₂) ∪ (E₁ ∩ E₂) = E₁

exclusive and exhaustive events

(c) If E₁ and E₂ have common (iii) E₁ ∩ E₂ = φ, E₁ ∪ E₂ = S

outcomes, then

(d) If E₁ and E₂ are two events (iv) E₁ ∩ E₂ = φ

such that E₁ ⊂ E₂

Sol.

\begin{array}{l} (a) I f E_{1} a n d E_{2} a r e m u t u a l l y e x c l u s i v e e v e n t s, t h e n E_{1} \cap E_{2} = ϕ . \\ (b) I f E_{1} a n d E_{2} a r e m u t u a l l y e x c l u s i v e a n d e x h a u s t i v e e v e n t s, t h e n \\ E_{1} \cap E_{2} = ϕ a n d E_{1} \cup E_{2} = S . \\ (c) I f E_{1} a n d E_{2} h a v e c o m m o n o u t c o m e s, t h e n (E_{1} - E_{2}) \cup (E_{1} \cap E_{2}) = E_{1} \\ (d) I f E_{1} a n d E_{2} a r e t w o e v e n t s s u c h t h a t E_{1} \subset E_{2} \Rightarrow E_{1} \cap E_{2} = E_{1} \\ H e n c e, (a) \leftrightarrow (i v), (b) \leftrightarrow (i i i), (c) \leftrightarrow (i i), (d) \leftrightarrow (i) \end{array}

Commonly asked questions

Match the following

(a) If E₁ and E₂ are the two mutually (i) E₁ ∩ E₂ = E₁ exclusive events

(b) If E₁ and E₂ are the mutually (ii) (E₁ – E₂) ∪ (E₁ ∩ E₂) = E₁

exclusive and exhaustive events

(c) If E₁ and E₂ have common (iii) E₁ ∩ E₂ = φ, E₁ ∪ E₂ = S

outcomes, then

(d) If E₁ and E₂ are two events (iv) E₁ ∩ E₂ = φ

such that E₁ ⊂ E₂

This is a matching answer type question as classified in NCERT Exemplar

$\begin{array}{l} (a) I f E_{1} a n d E_{2} a r e m u t u a l l y e x c l u s i v e e v e n t s, t h e n E_{1} \cap E_{2} = ? . \\ (b) I f E_{1} a n d E_{2} a r e m u t u a l l y e x c l u s i v e a n d e x h a u s t i v e e v e n t s, t h e n \\ E_{1} \cap E_{2} = ? a n d E_{1} \cup E_{2} = S . \\ (c) I f E_{1} a n d E_{2} h a v e c o m m o n o u t c o m e s, t h e n (E_{1} - E_{2}) \cup (E_{1} \cap E_{2}) = E_{1} \\ (d) I f E_{1} a n d E_{2} a r e t w o e v e n t s s u c h t h a t E_{1} \subset E_{2} \Rightarrow E_{1} \cap E_{2} = E_{1} \\ H e n c e, (a) \leftrightarrow (i v), (b) \leftrightarrow (i i i), (c) \leftrightarrow (i i), (d) \leftrightarrow (i) \end{array}$

Match the proposed probability under Column C₁ with the appropriate written description under column C₂ :

C₁ C₂

Probability Written Description

(a) 0.95 (i) An incorrect assignment

(b) 0.02 (ii) No chance of happening

(c) – 0.3 (iii) As much chance of happening as not.

(d) 0.5 (iv) Very likely to happen

(e) 0 (v) Very little chance of happening

This is a matching answer type question as classified in NCERT Exemplar

$\begin{array}{l} (a) 0.95 = V e r y l i k e l y t o h a p p e n, s o i t i s c l o s e t o 1 . \\ (b) 0.02 = V e r y l i t t l e c h a n c e o f h a p p e n i n g a s t h e p r o b a b i l i t y i s v e r y l o w . \\ (c) - 0.3 = A n i n c o r r e c t a s s i g n m e n t b e c a u s e p r o b a b i l i t y i s n e v e r n e g a t i v e . \\ (d) 0.5 = A s m u c h c h a n c e o f h a p p e n i n g a s n o t b e c a u s e s u m o f c h a n c e s o f h a p p e n i n g \\ a n d n o t h a p p e n i n g i s o n e . \\ (e) 0 = N o c h a n c e o f h a p p e n i n g . \\ H e n c e, (a) \leftrightarrow (i v), (b) \leftrightarrow (v), (c) \leftrightarrow (i), (d) \leftrightarrow (i i i), (e) \leftrightarrow (i i) \end{array}$

Maths NCERT Exemplar Solutions Class 11th Chapter Sixteen Exam

Student Forum

Anything you would want to ask experts?

Write here...

Other Similar chapters for you

Probability

News & Updates

Latest NewsPopular News

Maths NCERT Exemplar Solutions Class 11th Chapter Sixteen: Overview, Questions, Preparation

Probability Short Answer Type Questions

Commonly asked questions

Probability Long Answer Type Questions

Commonly asked questions

Probability Objective Type Questions

Commonly asked questions

Probability True or False Type Questions

Commonly asked questions

Probability Fill in the blank Type Questions

Commonly asked questions

Probability Matching Type Questions

Commonly asked questions

Student Forum

Other Similar chapters for you

News & Updates

JEE Main 2026 Application Form Live: NTA Registration Last Date To Apply November 27; Latest Updates

IBPS Clerk 2025 Prelims Cut off & Scorecard Releases Soon; Check Details

Board Exam Date Sheet 2026 Class 10, 12 Live Updates: Check CBSE, Maharashtra Board, UP Board, GSEB, HBSE Date Sheet

JEE Main Marks vs Percentile vs Rank 2025: Calculate Percentile and Rank Using Marks

List of NIT Colleges in India 2025 - NIRF Ranking, Courses, Seats, Cutoff, Fees and Placement

CBSE 10th Maths Question Paper 2025, 2024, 2023, 2022, 2020, 2019 PDF Download

NEET Chapter Wise Weightage 2026 PDF by NTA: Physics, Chemistry & Biology

List of Top IITs in India 2025: NIRF Ranking, Courses, Seats, Fees & Placement