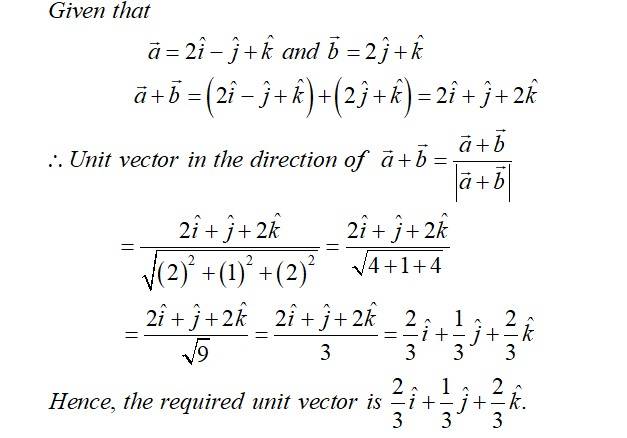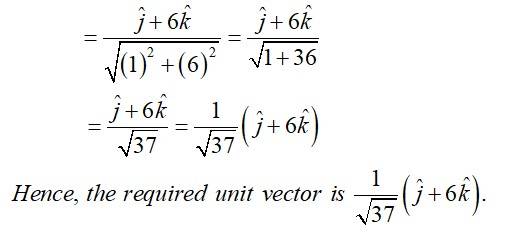The angle between two vectors a → , b → with magnitudes √3 and 4, respectively, and a → . b → = 2√3 is: (A) π 6 (B) π 3 (C) π 2 (D) 5 π 2

This is a Objective type Questions as classified in NCERT Exemplar Sol: H e r e , g i v e n t h a t | a → | = 3 , | b → | = 4 a n d a → . b → = 2 3 ∴ F r o m s c a l a r p r o d u c t , w e k n o w t h a t a → . b → = | a → | | b → | c o s θ ⇒ 2 3 = 3 . 4 . c o s θ ⇒ c o s θ = 2 3 3 . 4 = 1 2 ∴ θ = π 3 H e n c e , t h e c o r r e c t o p t i o n i s ( b ) .

Find the value of λ such that the vectors a → = 2î + λĵ + k̂ and b → = î + 2ĵ + 3k̂ are orthogonal. (A) 0 (B) 1 (C) 3 2 (D) − 5 2

This is an Objective type Questions as classified in NCERT Exemplar Sol: G i v e n t h a t a → = 2 i ^ + λ j ^ + k ^ a n d b → = i ^ + 2 j ^ + 3 k ^ Since a→ and b→ are orthogonal ∴ a → . b → = 0 ⇒ ( 2 i ^ + λ j ^ + k ^ ) . ( i ^ + 2 j ^ + 3 k ^ ) = 0 ⇒ 2 + 2 λ + 3 = 0 ⇒ 5 + 2 λ = 0 ⇒ λ = − 5 2 H e n c e , t h e c o r r e c t o p t i o n i s ( d ) .

Find the unit vector in the direction of the sum of vectors a → = î − 2ĵ + k̂ and b → = ĵ + 2k̂.

This is a Short Answer type Questions as classified in NCERT Exemplar Sol: G i v e n t h a t a → = 2 i ^ − j ^ + k ^ a n d b → = 2 j ^ + k ^ a → + b → = ( 2 i ^ − j ^ + k ^ ) + ( 2 j ^ + k ^ ) = 2 i ^ + j ^ + 2 k ^ ∴ U n i t v e c t o r i n t h e d i r e c t i o n o f a → + b → = a → + b → | a → + b → | = 2 i ^ + j ^ + 2 k ^ ( 2 ) 2 + ( 1 ) 2 + ( 2 ) 2 = 2 i ^ + j ^ + 2 k ^ 4 + 1 + 4 = 2 i ^ + j ^ + 2 k ^ 9 = 2 i ^ + j ^ + 2 k ^ 3 = 2 3 i ^ + 1 3 j ^ + 2 3 k ^ H e n c e , t h e r e q u i r e d u n i t v e c t o r i s 2 3 i ^ + 1 3 j ^ + 2 3 k ^ .

Find a unit vector in the direction of PQ → , where P and Q have coordinates (5, 0, 8) and (3, 3, 2), respectively.

This is a Short Answer type Questions as classified in NCERT Exemplar Sol: G i v e n c o o r d i n a t e s a r e P ( 5 , 0 , 8 ) a n d Q ( 3 , 3 , 2 ) ∴ P Q → = ( 3 − 5 ) i ^ + ( 3 − 0 ) j ^ + ( 2 − 8 ) k ^ = − 2 i ^ + 3 j ^ − 6 k ^ ∴ U n i t v e c t o r i n t h e d i r e c t i o n o f P Q → = P Q → | P Q → | = − 2 i ^ + 3 j ^ − 6 k ^ ( − 2 ) 2 + ( 3 ) 2 + ( − 6 ) 2 = − 2 i ^ + 3 j ^ − 6 k ^ 4 + 9 + 3 6 = − 2 i ^ + 3 j ^ − 6 k ^ 4 9 = − 2 i ^ + 3 j ^ − 6 k ^ 7 = 1 7 ( − 2 i ^ + 3 j ^ − 6 k ^ ) H e n c e , t h e r e q u i r e d u n i t v e c t o r i s 1 7 ( − 2 i ^ + 3 j ^ − 6 k ^ ) .

The sum, of all real values of x for which 3 x 2 − 9 x + 1 7 x 2 + 3 x + 1 0 = 5 x 2 − 7 x + 1 9 3 x 2 + 5 x + 1 2 is equal to…………….

3 x 2 − 9 x + 1 7 x 2 + 3 x + 1 0 = 5 x 2 − 7 x + 1 9 3 x 2 + 5 x + 1 2 1 + 2 x 2 − 1 2 x + 7 x 2 + 3 x + 1 0 = 1 + 2 x 2 − 1 2 x + 7 3 x 2 + 5 x + 1 2 ( 2 x 2 − 1 2 x + 7 ) ( 1 x 2 + 3 x + 1 0 − 1 3 x 2 + 5 x + 1 2 ) = 0

If ∫ 0 3 1 5 x 3 1 + x 2 + ( 1 + x 2 ) 3 d x = α 2 + β 3 , where a, b are integers, then α + β is equal to………..

Put 1 + x 2 = t 2 ⇒ 2 x d x = 2 t d t ∴ ∫ 1 2 1 5 ( t 2 − 1 ) t d t t 2 + t 3 d t Put (1 + t) = u2 3 0 ∫ 2 3 ( u 4 − 2 u 2 ) d u dt = 2u du = − 6 3 + 1 6 2 = α 2 + β 3 α = 1 6 , β = − 6 ∴ α + β = 1 0

If the system of linear equations 2x + 3y – z = 2 x + y + z = 4 x−y+|λ|z=4λ−4 where λ∈R, has no solution, then

System of equation is (23−1111−1|λ|) (xyz)= [−244λ−4] R1 – 2 R2, R3 – R2 (01−3110−2|λ|−1) (xyz)= (−10 44λ−8) System of equation will have no solution for λ = 7.

Let the solution curve y = y(x) of the differential equation [ x x 2 − y 2 + e y x ] x d y d x = x + [ x x 2 − y 2 + e y x ] y pass through the points (1, 0) and (2α, α), α > 0. Then a is equal to

[xx2−y2+ey/x]xdydx=x+[xx2−y2+ey/x]y ⇒ey/x[x dy−y dx]=x dx+xx2−y2(y dx−x dy) ⇒ey/xd(y/x)=dxx−d(y/x)1−(y/x)2 Integrating ey/x=lnx−sin−1(yx)+c Passes (1, 0) 1 = c ⇒α=12exp(e−1+π6)

Let AB and PQ be two vertical poles, 160m apart from each other. Let C be the middle points of B and Q, which are feet of these two poles. Let π 8 and q be the angles of elevation from C to P and A, respectively. If the height of pole PQ is twice the height of pole AB, then tan2q is equal to

tanπ8=2h80......... (i) tanθ=h80.......... (ii) ⇒tanπ8=2tanθ tan2θ=3−224

State True or False for the statement in each of the Exercises 41 to 45. If | a → | =| b → | , then necessarily it implies a → = ± b →

This is a True or False type Questions as classified in NCERT Exemplar Sol: I f | a → | = | b → | t h e n a → = ± b → w h i c h i s t r u e . H e n c e t h e g i v e n s t a t e m e n t i s T r u e .

If | a → + b → | = | a → - b → | , then the vectors a → and b → are orthogonal.

This is a True or False type Questions as classified in NCERT Exemplar Sol: G i v e n t h a t | a → + b → | = | a → − b → | S q u a r i n g b o t h s i d e s , w e g e t | a → + b → | 2 = | a → − b → | 2 ⇒ | a → | 2 + | b → | 2 + 2 a → . b → = | a → | 2 + | b → | 2 − 2 a → . b → ⇒ 2 a → . b → = − 2 a → . b → ⇒ a → . b → = − a → . b → ⇒ 2 a → . b → = 0 ⇒ a → . b → = 0 w h i c h i m p l i e s t h a t a → a n d b → a r e o r t h o g o n a l . H e n c e t h e g i v e n s t a t e m e n t i s T r u e .

The formula ( a → + b → ) 2 + ( a → 2 + b → 2 ) + 2 ( a → × b → ) 2 is valid for non-zero vectors a → and b → .

This is a True or False type Questions as classified in NCERT Exemplar Sol: ( a → + b → ) 2 = ( a → + b → ) . ( a → + b → ) = | a → | 2 + | b → | 2 + 2 a → . b → H e n c e t h e g i v e n s t a t e m e n t i s F a l s e .

If a → ⋅ and b → are adjacent sides of a rhombus, then a → ⋅ b → = 0.

This is a True or False type Questions as classified in NCERT Exemplar Sol: I f a → . b → = 0 t h e n a → . b → = | a → | | b → | c o s 9 0 0 So the angle between the adjacent sides of the rhombus should be 900 which is not possible. H e n c e t h e g i v e n s t a t e m e n t i s F a l s e .

Show that the area of the parallelogram whose diagonals are given by a → and b → is 1 2 ∣ a → × b → 2 ∣ Also, find the area of the parallelogram whose diagonals are 2î − ĵ + k̂ and î + 3ĵ − k̂.

This is a Long Answer type Questions as classified in NCERT Exemplar Let ABCD be a parallelogram such that, A B → = p → , A D → = q → = B C → ∴ b y l a w o f t r i a n g l e , w e g e t A C → = a → = p → + q → … ( i ) a n d B D → = b → = − p → + q → … ( i i ) A d d i n g e q . ( i ) a n d ( i i ) w e g e t , a → + b → = 2 q → ⇒ q → = ( a → + b → 2 ) S u b t r a c t i n g e q . ( i i ) f r o m ( i ) w e g e t , a → − b → = 2 p → ⇒ p → = ( a → − b → 2 ) ∴ p → × q → = 1 4 ( a → + b → ) ( a → − b → ) = 1 4 ( a → × a → − a → × b → + b → × a → − b → × b → ) = 1 4 ( − a → × b → + b → × a → ) [ ? a → × a → = 0 b → × b → = 0 ] = 1 4 ( a → × b → + b → × a → ) = 1 4 . 2 ( a → × b → ) = | a → × b → | 2 So, the area of parallelogram ABCD=|p→×q→|=12|a→×b→| Now area of parallelogram whose diagonals are 2i^−j^+k^ and i^+3j^−k^ = 1 2 | ( 2 i ^ − j ^ + k ^ ) × ( i ^ + 3 j ^ − k ^ ) | = 1 2 | i ^ j ^ k ^ 2 − 1 1 1 3 − 1 | = 1 2 [ i ^ ( 1 − 3 ) − j ^ ( − 2 − 1 ) + k ^ ( 6 + 1 ) ] = 1 2 | − 2 i ^ + 3 j ^ + 7 k ^ | = 1 2 ( − 2 ) 2 + ( 3 ) 2 + ( 7 ) 2 = 1 2 4 + 9 + 4 9 = 1 2 6 2 s q . u n i t s . H e n c e , t h e r e q u i r e d a r e a i s 1 2 6 2 s q . u n i t s .

If a → = î + ĵ + k̂ and b̂ = ĵ − k̂, find a vector c such that a → × c → = b → and a → . c → = 3.

This is a Long Answer type Questions as classified in NCERT Exemplar Sol: L e t c → = c 1 i ^ + c 2 j ^ + c 3 k ^ A l s o g i v e n t h a t a → = i ^ + j ^ + k ^ a n d b → = j ^ − k ^ S i n c e , a → × c → = b → ∴ | i ^ j ^ k ^ 1 1 1 c 1 c 2 c 3 | = j ^ − k ^ i ^ ( c 3 − c 2 ) − j ^ ( c 3 − c 1 ) + k ^ ( c 2 − c 1 ) = j ^ − k ^ O n c o m p a r i n g t h e l i k e t e r m s , w e g e t c 3 − c 2 = 0 … ( i ) c 1 − c 3 = 1 … ( i i ) c 2 − c 1 = − 1 … ( i i i ) N o w f o r a → . c → = 3 ( i ^ + j ^ + k ^ ) . ( c 1 i ^ + c 2 j ^ + c 3 k ^ ) = 3 ∴ c 1 + c 2 + c 3 = 3 … ( i v ) A d d i n g e q . ( i i ) a n d e q . ( i i i ) w e g e t , c 2 − c 3 = 0 … ( v ) F r o m ( i v ) a n d ( v ) w e g e t c 1 + 2 c 2 = 3 … ( v i ) F r o m ( i i i ) a n d ( v i ) w e g e t c 1 + 2 c 2 = 3 − c 1 + c 2 = − 1 _ A d d i n g 3 c 2 = 2 ∴ c 2 = 2 3 c 3 − c 2 = 0 ⇒ c 3 − 2 3 = 0 ∴ c 3 = 2 3 N o w , c 2 − c 1 = − 1 ⇒ 2 3 − c 1 = − 1 ⇒ c 1 = 1 + 2 3 = 5 3 ∴ c → = 5 3 i ^ + 2 3 j ^ + 2 3 k ^ = 1 3 ( 5 i ^ + 2 j ^ + 2 k ^ ) H e n c e , c → = 1 3 ( 5 i ^ + 2 j ^ + 2 k ^ ) .

If r → . a → = 0, r → . b → = 0, r → . c → = 0 for some non-zero vector r̂, then the value of ( a → × b → ) ĉ is ________.

This is a Fill in the blanks type Questions as classified in NCERT Exemplar Sol: I f r → i s a n o n − z e r o v e c t o r , t h e n a → , b → a n d c → c a n b e i n t h e s a m e p l a n e . Since angles between a→, b→ and c→ are zero i.e. θ=0 ∴ a → . ( b → × c → ) = 0 H e n c e , t h e r e q u i r e d v a l u e i s 0 .

The values of k for which |k a → and k a → + 1 2 a → is parallel to a → holds true are ________.

This is a Fill in the blanks type Questions as classified in NCERT Exemplar Sol: G i v e n t h a t | k a → | < | a → | a n d k a → + 1 2 a → i s p a r a l l e l t o a → ∴ | k a → | < | a → | ⇒ | k | | a → | < | a → | ⇒ | k | < 1 ⇒ − 1 < k < 1 Now since ka→+12a→ is parallel to a→ H e r e , w e s e e t h a t k = − 1 2 , k a → + 1 2 a → b e c o m e n u l l v e c t o r a n d t h e n i t w i l l n o t b e p a r a l l e l t o a → . ∴ k a → + 1 2 a → i s p a r a l l e l t o a → w h e n k ∈ ( − 1 , 1 ) a n d k ≠ 1 2 . H e n c e , t h e r e q u i r e d v a l u e o f k ∈ ( − 1 , 1 ) a n d k ≠ 1 2 .

The value of the expression ( a → × b ? ) 2 + ( a → . b → ) 2 is ________.

This is a Fill in the blanks type Questions as classified in NCERT Exemplar Sol: | a → × b → | 2 + ( a → . b → ) 2 = ( | a → | | b → | s i n θ ) 2 + ( | a → | | b → | c o s θ ) 2 = | a → | 2 | b → | 2 s i n 2 θ + | a → | 2 | b → | 2 c o s 2 θ = | a → | 2 | b → | 2 . ( s i n 2 θ + c o s 2 θ ) = | a → | 2 | b → | 2 . 1 = | a → | 2 | b → | 2 H e n c e , t h e v a l u e o f t h e f i l l e r i s | a → | 2 | b → | 2 .

Maths NCERT Exemplar Solutions Class 12th Chapter Ten: Overview, Questions, Preparation

Updated on Jul 24, 2025 12:06 IST

By alok kumar singh, Executive Content Operations

Table of content

Vector Algebra Short Answer Type Questions
Vector Algebra Long Answer Type Questions
Vector Algebra Objective Type Questions
Vector Algebra Fill in the blanks
Vector Algebra True or False Type Question
28th June 2022 (First Shift)
JEE Mains 2022

Vector Algebra Short Answer Type Questions

1. Find the unit vector in the direction of the sum of vectors $\vec{a}$ = î − 2ĵ + k̂ and $\vec{b}$ = ĵ + 2k̂.

Sol:

2. If â = î + ĵ + 2k̂ and b̂ = î + 2ĵ − 2k̂, find the unit vector in the direction of
(i) 6 $\vec{b}$
(ii) 2 $\vec{a}$ − $\vec{b}$ .

Sol:

Commonly asked questions

Find the unit vector in the direction of the sum of vectors $\vec{a}$ = î − 2ĵ + k̂ and $\vec{b}$ = ĵ + 2k̂.

This is a Short Answer type Questions as classified in NCERT Exemplar

Sol:

\begin{array}{l} G i v e n t h a t \\ \vec{a} = 2 \hat{i} - \hat{j} + \hat{k} a n d \vec{b} = 2 \hat{j} + \hat{k} \\ \vec{a} + \vec{b} = (2 \hat{i} - \hat{j} + \hat{k}) + (2 \hat{j} + \hat{k}) = 2 \hat{i} + \hat{j} + 2 \hat{k} \\ ∴ U n i t v e c t o r i n t h e d i r e c t i o n o f \vec{a} + \vec{b} = \frac{\vec{a} + \vec{b}}{| \vec{a} + \vec{b} |} \\ = \frac{2 \hat{i} + \hat{j} + 2 \hat{k}}{\sqrt[]{{(2)}^{2} + {(1)}^{2} + {(2)}^{2}}} = \frac{2 \hat{i} + \hat{j} + 2 \hat{k}}{\sqrt[]{4 + 1 + 4}} \\ = \frac{2 \hat{i} + \hat{j} + 2 \hat{k}}{\sqrt[]{9}} = \frac{2 \hat{i} + \hat{j} + 2 \hat{k}}{3} = \frac{2}{3} \hat{i} + \frac{1}{3} \hat{j} + \frac{2}{3} \hat{k} \\ H e n c e, t h e r e q u i r e d u n i t v e c t o r i s \frac{2}{3} \hat{i} + \frac{1}{3} \hat{j} + \frac{2}{3} \hat{k} . \end{array}

If â = î + ĵ + 2k̂ and b̂ = î + 2ĵ − 2k̂, find the unit vector in the direction of
(i) 6 $\vec{b}$
(ii) 2 $\vec{a}$ − $\vec{b}$ .

This is a Short Answer type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n t h a t \vec{a} = \hat{i} + \hat{j} + 2 \hat{k} a n d \vec{b} = 2 \hat{i} + \hat{j} - 2 \hat{k} \\ (i) 6 \vec{b} = 6 (2 \hat{i} + \hat{j} - 2 \hat{k}) = 12 \hat{i} + 6 \hat{j} - 12 \hat{k} \\ ∴ U n i t v e c t o r i n t h e d i r e c t i o n o f 6 \vec{b} = \frac{6 \vec{b}}{| 6 \vec{b} |} \\ = \frac{12 \hat{i} + 6 \hat{j} - 12 \hat{k}}{\sqrt[]{{(12)}^{2} + {(6)}^{2} + {(- 12)}^{2}}} = \frac{12 \hat{i} + 6 \hat{j} - 12 \hat{k}}{\sqrt[]{144 + 36 + 144}} \\ = \frac{12 \hat{i} + 6 \hat{j} - 12 \hat{k}}{\sqrt[]{324}} = \frac{12 \hat{i} + 6 \hat{j} - 12 \hat{k}}{18} \\ = \frac{6}{18} (2 \hat{i} + \hat{j} - 2 \hat{k}) = \frac{1}{3} (2 \hat{i} + \hat{j} - 2 \hat{k}) \\ H e n c e, t h e r e q u i r e d u n i t v e c t o r i s \frac{1}{3} (2 \hat{i} + \hat{j} - 2 \hat{k}) . \\ (i i) 2 \vec{a} - \vec{b} = 2 (\hat{i} + \hat{j} + 2 \hat{k}) - (2 \hat{i} + \hat{j} - 2 \hat{k}) \\ = 2 \hat{i} + 2 \hat{j} + 4 \hat{k} - 2 \hat{i} - \hat{j} + 2 \hat{k} = \hat{j} + 6 \hat{k} \\ ∴ U n i t v e c t o r i n t h e d i r e c t i o n o f 2 \vec{a} - \vec{b} = \frac{2 \vec{a} - \vec{b}}{| 2 \vec{a} - \vec{b} |} \\ = \frac{\hat{j} + 6 \hat{k}}{\sqrt[]{{(1)}^{2} + {(6)}^{2}}} = \frac{\hat{j} + 6 \hat{k}}{\sqrt[]{1 + 36}} \\ = \frac{\hat{j} + 6 \hat{k}}{\sqrt[]{37}} = \frac{1}{\sqrt[]{37}} (\hat{j} + 6 \hat{k}) \\ H e n c e, t h e r e q u i r e d u n i t v e c t o r i s \frac{1}{\sqrt[]{37}} (\hat{j} + 6 \hat{k}) . \end{array}$

Find a unit vector in the direction of $\vec{PQ}$ , where P and Q have coordinates (5, 0, 8) and (3, 3, 2), respectively.

This is a Short Answer type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n c o o r d i n a t e s a r e P (5, 0, 8) a n d Q (3, 3, 2) \\ ∴ \vec{P Q} = (3 - 5) \hat{i} + (3 - 0) \hat{j} + (2 - 8) \hat{k} = - 2 \hat{i} + 3 \hat{j} - 6 \hat{k} \\ ∴ U n i t v e c t o r i n t h e d i r e c t i o n o f \vec{P Q} = \frac{\vec{P Q}}{| \vec{P Q} |} \\ = \frac{- 2 \hat{i} + 3 \hat{j} - 6 \hat{k}}{\sqrt[]{{(- 2)}^{2} + {(3)}^{2} + {(- 6)}^{2}}} = \frac{- 2 \hat{i} + 3 \hat{j} - 6 \hat{k}}{\sqrt[]{4 + 9 + 36}} \\ = \frac{- 2 \hat{i} + 3 \hat{j} - 6 \hat{k}}{\sqrt[]{49}} = \frac{- 2 \hat{i} + 3 \hat{j} - 6 \hat{k}}{7} \\ = \frac{1}{7} (- 2 \hat{i} + 3 \hat{j} - 6 \hat{k}) \\ H e n c e, t h e r e q u i r e d u n i t v e c t o r i s \frac{1}{7} (- 2 \hat{i} + 3 \hat{j} - 6 \hat{k}) . \end{array}$

If $\vec{a}$ and $\vec{b}$ . are the position vectors of A and B, respectively, find the position vector of a point C in BA produced such that BC = 1.5 BA.

This is a Short Answer type Questions as classified in NCERT Exempla

$\begin{array}{l} G i v e n t h a t B C = 1.5 B A \\ \Rightarrow \frac{B C}{B A} = 1.5 = \frac{3}{2} \\ \Rightarrow \frac{\vec{c} - \vec{b}}{\vec{a} - \vec{b}} = \frac{3}{2} \\ \Rightarrow 2 \vec{c} - 2 \vec{b} = 3 \vec{a} - 3 \vec{b} \Rightarrow 2 \vec{c} = 3 \vec{a} - 3 \vec{b} + 2 \vec{b} \\ \Rightarrow 2 \vec{c} = 3 \vec{a} - \vec{b} \\ ∴ \vec{c} = \frac{3 \vec{a} - \vec{b}}{2} \\ H e n c e, t h e r e q u i r e d v e c t o r i s \vec{c} = \frac{3 \vec{a} - \vec{b}}{2} . \end{array}$

Using vectors, find the value of k such that the points (k, –10, 3), (1, –1, 3), and (3, 5, 3) are collinear.

This is a Short Answer type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} L e t t h e g i v e n points a r e A (k, - 10, 3), B (1, - 1, 3) a n d C (3, 5, 3) \\ \vec{A B} = (1 - k) \hat{i} + (- 1 + 10) \hat{j} + (3 - 3) \hat{k} = (1 - k) \hat{i} + 9 \hat{j} + 0 \hat{k} \\ ∴ | \vec{A B} | = \sqrt[]{{(1 - k)}^{2} + {(9)}^{2}} = \sqrt[]{{(1 - k)}^{2} + 81} \\ \vec{B C} = (3 - 1) \hat{i} + (5 + 1) \hat{j} + (3 - 3) \hat{k} = 2 \hat{i} + 6 \hat{j} + 0 \hat{k} \\ ∴ | \vec{B C} | = \sqrt[]{{(2)}^{2} + {(6)}^{2}} = \sqrt[]{4 + 36} = \sqrt[]{40} = 2 \sqrt[]{10} \\ \vec{A C} = (3 - k) \hat{i} + (5 + 10) \hat{j} + (3 - 3) \hat{k} = (3 - k) \hat{i} + 6 \hat{j} + 0 \hat{k} \\ ∴ | \vec{A C} | = \sqrt[]{{(3 - k)}^{2} + {(15)}^{2}} = \sqrt[]{{(3 - k)}^{2} + 225} \\ I f A, B, a n d C a r e c o l l i n e a r, t h e n \\ | \vec{A B} | + | \vec{B C} | = | \vec{A C} | \\ \sqrt[]{{(1 - k)}^{2} + 81} + 2 \sqrt[]{10} = \sqrt[]{{(3 - k)}^{2} + 225} \\ S q u a r i n g b o t h s i d e s, w e h a v e \\ {[\sqrt[]{{(1 - k)}^{2} + 81} + \sqrt[]{40}]}^{2} = {[\sqrt[]{{(3 - k)}^{2} + 225}]}^{2} \\ \Rightarrow {(1 - k)}^{2} + 81 + 40 + 2 \sqrt[]{40} \sqrt[]{{(1 - k)}^{2} + 81} = {(3 - k)}^{2} + 225 \\ \Rightarrow 1 + k^{2} - 2 k + 121 + 2 \sqrt[]{40} \sqrt[]{1 + k^{2} - 2 k + 81} = 9 + k^{2} - 6 k + 225 \\ \Rightarrow 122 - 2 k + 2 \sqrt[]{40} \sqrt[]{k^{2} - 2 k + 82} = 234 - 6 k \\ D i v i d i n g b y 2, w e g e t \\ \Rightarrow 61 - k + \sqrt[]{40} \sqrt[]{k^{2} - 2 k + 82} = 117 - 3 k \\ \Rightarrow \sqrt[]{40} \sqrt[]{k^{2} - 2 k + 82} = 117 - 61 - 3 k + k \\ \Rightarrow \sqrt[]{40} \sqrt[]{k^{2} - 2 k + 82} = 56 - 2 k \\ \Rightarrow 2 \sqrt[]{10} \sqrt[]{k^{2} - 2 k + 82} = 56 - 2 k \\ \Rightarrow \sqrt[]{10} \sqrt[]{k^{2} - 2 k + 82} = 28 - k (D i v i d i n g b y 2) \\ S q u a r i n g b o t h s i d e s, w e g e t \\ \Rightarrow 10 (k^{2} - 2 k + 82) = 784 + k^{2} - 56 k \\ \Rightarrow 10 k^{2} - 20 k + 820 = 784 + k^{2} - 56 k \\ \Rightarrow 10 k^{2} - k^{2} - 20 k + 56 k + 820 - 784 = 0 \\ \Rightarrow 9 k^{2} + 36 k + 36 = 0 \Rightarrow k^{2} + 4 k + 4 = 0 \\ \Rightarrow {(k + 2)}^{2} = 0 \Rightarrow k + 2 = 0 \Rightarrow k = - 2 \\ H e n c e, t h e r e q u i r e d v a l u e i s k = - 2 . \end{array}$

A vector $\vec{r}$ . is inclined at equal angles to the three axes. If the magnitude of $r$ . is 2 $\sqrt[]{3}$ units, find $\vec{r}$ .

This is a Short Answer type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} Since, t h e v e c t o r \vec{r} m a k e s e q u a l a n g l e s w i t h t h e a x e s, t h e i r d i r e c t i o n c o s i n e s s h o u l d b e s a m e . \\ ∴ l = m = n \\ W e k n o w t h a t l^{2} + m^{2} + n^{2} = 1 \Rightarrow l^{2} + l^{2} + l^{2} = 1 \\ \Rightarrow 3 l^{2} = 1 \Rightarrow l^{2} = \frac{1}{3} \Rightarrow l = \pm \frac{1}{\sqrt[]{3}} \\ ∴ \hat{r} = \pm \frac{1}{\sqrt[]{3}} \hat{i} \pm \frac{1}{\sqrt[]{3}} \hat{j} \pm \frac{1}{\sqrt[]{3}} \hat{k} \Rightarrow \hat{r} = \pm \frac{1}{\sqrt[]{3}} (\hat{i} + \hat{j} + \hat{k}) \\ W e k n o w t h a t \vec{r} = (\hat{r}) | \vec{r} | \\ = \pm \frac{1}{\sqrt[]{3}} (\hat{i} + \hat{j} + \hat{k}) 2 \sqrt[]{3} = \pm 2 (\hat{i} + \hat{j} + \hat{k}) \\ H e n c e, t h e r e q u i r e d v a l u e o f \vec{r} i s \pm 2 (\hat{i} + \hat{j} + \hat{k}) . \end{array}$

A vector has magnitude 14 and direction ratios 2, 3, –6. Find the direction cosines and components of r?, given that makes an acute angle with the x-axis.

This is a Short Answer type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} L e t \vec{a}, \vec{b} a n d \vec{c} b e t h r e e v e c t o r s s u c h t h a t \vec{a} = 2 k, \vec{b} = 3 k a n d \vec{c} = - 6 k \\ I f l, m a n d n a r e t h e d i r e c t i o n s c o s i n e s o f v e c t o r \vec{r}, t h e n \\ l = \frac{\vec{a}}{| \vec{r} |} = \frac{2 k}{14} = \frac{k}{7} \\ m = \frac{\vec{b}}{| \vec{r} |} = \frac{3 k}{14} a n d n = \frac{\vec{c}}{| \vec{r} |} = \frac{- 6 k}{14} = \frac{- 3 k}{7} \\ W e k n o w t h a t l^{2} + m^{2} + n^{2} = 1 \Rightarrow \frac{k^{2}}{49} + \frac{9 k^{2}}{196} + \frac{9 k^{2}}{49} = 1 \\ \Rightarrow \frac{4 k^{2} + 9 k^{2} + 36 k^{2}}{196} = 1 \Rightarrow 49 k^{2} = 196 \Rightarrow k^{2} = 4 \\ ∴ k = \pm 2 a n d l = \frac{k}{7} = \frac{2}{7} \\ m = \frac{3 k}{14} = \frac{3 \times 2}{14} = \frac{3}{7} a n d n = \frac{- 3 k}{7} = \frac{- 3 \times 2}{7} = \frac{- 6}{7} \\ ∴ \hat{r} = \pm (\frac{2}{7} \hat{i} + \frac{3}{7} \hat{j} - \frac{6}{7} \hat{k}) \\ W e k n o w t h a t \vec{r} = (\hat{r}) | \vec{r} | \\ = \pm (\frac{2}{7} \hat{i} + \frac{3}{7} \hat{j} - \frac{6}{7} \hat{k}) . 14 = \pm (4 \hat{i} + 6 \hat{j} - 12 \hat{k}) \\ H e n c e, t h e r e q u i r e d d i r e c t i o n c o s i n e s a r e \frac{2}{7}, \frac{3}{7}, \frac{- 6}{7} a n d t h e c o m p o n e n t s o f \vec{r} a r e 4 \hat{i}, 6 \hat{j} a n d - 12 \hat{k} . \end{array}$

Find a vector of magnitude 6, which is perpendicular to both the vectors 2î − 2ĵ + k̂ and 4î − 3ĵ + k̂.

This is a Short Answer type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} L e t \vec{a} = 2 \hat{i} - \hat{j} + 2 \hat{k} a n d \vec{b} = 4 \hat{i} - \hat{j} + 3 \hat{k} \\ W e k n o w t h a t u n i t v e c t o r a r e p e r p e n d i c u l a r t o \vec{a} a n d \vec{b} = \frac{(\vec{a} \times \vec{b})}{| \vec{a} \times \vec{b} |} \\ \vec{a} \times \vec{b} = | \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & - 1 & 2 \\ 4 & - 1 & 3 \end{matrix} | \\ = \hat{i} (- 3 + 2) - \hat{j} (6 - 8) + \hat{k} (- 2 + 4) = - \hat{i} + 2 \hat{j} + 2 \hat{k} \\ ∴ | \vec{a} \times \vec{b} | = \sqrt[]{{(- 1)}^{2} + {(2)}^{2} + {(2)}^{2}} = \sqrt[]{1 + 4 + 4} = \sqrt[]{9} = 3 \\ S o, \frac{(\vec{a} \times \vec{b})}{| \vec{a} \times \vec{b} |} = \frac{- \hat{i} + 2 \hat{j} + 2 \hat{k}}{3} = \frac{1}{3} (- \hat{i} + 2 \hat{j} + 2 \hat{k}) \\ N o w t h e v e c t o r o f m a g n i t u d e 6 = \frac{1}{3} (- \hat{i} + 2 \hat{j} + 2 \hat{k}) . 6 \\ = 2 (- \hat{i} + 2 \hat{j} + 2 \hat{k}) = - 2 \hat{i} + 4 \hat{j} + 4 \hat{k} \\ H e n c e, t h e r e q u i r e d v e c t o r i s - 2 \hat{i} + 4 \hat{j} + 4 \hat{k} . \end{array}$

Find the angle between the vectors 2î − ĵ + k̂ and 3î + 4ĵ − k̂.

This is a Short Answer type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} L e t \vec{a} = 2 \hat{i} - \hat{j} + \hat{k} a n d \vec{b} = 3 \hat{i} + 4 \hat{j} - \hat{k} \\ a n d l e t θ b e t h e a n g l e b e t w e e n \vec{a} a n d \vec{b} . \\ ∴ c o s θ = \frac{\vec{a} . \vec{b}}{| \vec{a} | | \vec{b} |} = \frac{(2 \hat{i} - \hat{j} + \hat{k}) (3 \hat{i} + 4 \hat{j} - \hat{k})}{\sqrt[]{4 + 1 + 1} . \sqrt[]{9 + 16 + 1}} \\ = \frac{6 - 4 - 1}{\sqrt[]{6} \sqrt[]{26}} = \frac{1}{2 \sqrt[]{3} . \sqrt[]{13}} = \frac{1}{2 \sqrt[]{39}} \\ ∴ θ = c o s^{- 1} \frac{1}{2 \sqrt[]{39}} \Rightarrow c o s^{- 1} (\frac{1}{156}) \\ H e n c e, t h e r e q u i r e d v a l u e o f θ i s c o s^{- 1} (\frac{1}{156}) . \end{array}$

If $\vec{a}$ + $\vec{b}$ + $\vec{c}$ = 0, show that $\vec{a}$ × $\vec{b}$ = $\vec{b}$ × $c$ = $\vec{c}$ × $\vec{a}$ . Interpret the result geometrically.

This is a Short Answer type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n t h a t \vec{a} + \vec{b} + \vec{c} = 0 \\ S o, \vec{a} \times (\vec{a} + \vec{b} + \vec{c}) = \vec{a} \times 0 \\ \Rightarrow \vec{a} \times \vec{a} + \vec{a} \times \vec{b} + \vec{a} \times \vec{c} = 0 \\ \Rightarrow \vec{0} + \vec{a} \times \vec{b} + \vec{a} \times \vec{c} = 0 (? \vec{a} \times \vec{a} = 0) \\ \Rightarrow \vec{a} \times \vec{b} - \vec{c} \times \vec{a} = 0 (\vec{a} \times \vec{c} = - \vec{c} \times \vec{a}) \\ \Rightarrow \vec{a} \times \vec{b} = \vec{c} \times \vec{a} \dots (i) \\ N o w, \vec{a} + \vec{b} + \vec{c} = 0 \\ \Rightarrow \vec{b} \times (\vec{a} + \vec{b} + \vec{c}) = \vec{b} \times 0 \\ \Rightarrow \vec{b} \times \vec{a} + \vec{b} \times \vec{b} + \vec{b} \times \vec{c} = 0 \\ \Rightarrow \vec{b} \times \vec{a} + \vec{0} + \vec{b} \times \vec{c} = 0 (? \vec{b} \times \vec{b} = 0) \\ \Rightarrow - (\vec{a} \times \vec{b}) + \vec{b} \times \vec{c} = 0 \\ \Rightarrow \vec{b} \times \vec{c} = \vec{a} \times \vec{b} \dots (i i) \\ F r o m e q . (i) a n d (i i) w e g e t \\ \vec{a} \times \vec{b} = \vec{b} \times \vec{c} = \vec{c} \times \vec{a} . H e n c e p r o v e d . \\ G e o m e t r i c a l I n t e r p r e t a t i o n \\ A c c o r d i n g t o f i g u r e, w e h a v e A r e a o f parallelogram A B C D i s \\ \Rightarrow | \vec{a} \times \vec{b} | = | \vec{a} | | \vec{b} | s i n θ \\ Since, t h e parallelograms o n t h e s a m e b a s e a n d b e t w e e n t h e s a m e p a r a l l e l l i n e s a r e \\ e q u a l i n a r e a . \\ ∴ | \vec{a} \times \vec{b} | = | \vec{b} \times \vec{c} | = | \vec{c} \times \vec{a} | \\ \Rightarrow \vec{a} \times \vec{b} = \vec{b} \times \vec{c} = \vec{c} \times \vec{a} . \end{array}$

Find the sine of the angle between the vectors $\vec{a}$ = 3î + 2ĵ + k̂ and $\vec{b}$ = −î + 2ĵ + 4k̂.

This is a Short Answer type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n t h a t \vec{a} = 3 \hat{i} + \hat{j} + 2 \hat{k} a n d \vec{b} = 2 \hat{i} - 2 \hat{j} + 4 \hat{k} \\ W e k n o w t h a t | \vec{a} \times \vec{b} | = | \vec{a} | | \vec{b} | s i n θ \\ ∴ \vec{a} \times \vec{b} = | \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ 3 & 1 & 2 \\ 2 & - 2 & 4 \end{matrix} | \\ = \hat{i} (4 + 4) - \hat{j} (12 - 4) + \hat{k} (- 6 - 2) \\ = 8 \hat{i} - 8 \hat{j} - 8 \hat{k} \\ ∴ | \vec{a} \times \vec{b} | = \sqrt[]{{(8)}^{2} + {(- 8)}^{2} + {(- 8)}^{2}} \\ = \sqrt[]{64 + 64 + 64} = \sqrt[]{192} = \sqrt[]{64 \times 3} = 8 \sqrt[]{3} \\ \Rightarrow | \vec{a} | = \sqrt[]{{(3)}^{2} + {(1)}^{2} + {(2)}^{2}} = \sqrt[]{9 + 1 + 4} = \sqrt[]{14} \\ \Rightarrow | \vec{b} | = \sqrt[]{{(2)}^{2} + {(- 2)}^{2} + {(4)}^{2}} = \sqrt[]{4 + 4 + 16} = \sqrt[]{24} = 2 \sqrt[]{6} \\ ∴ s i n θ = \frac{| \vec{a} \times \vec{b} |}{| \vec{a} | | \vec{b} |} = \frac{8 \sqrt[]{3}}{\sqrt[]{14} . 2 \sqrt[]{6}} = \frac{4 \sqrt[]{3}}{\sqrt[]{84}} = \frac{4 \sqrt[]{3}}{2 \sqrt[]{21}} = \frac{2}{\sqrt[]{7}} \\ H e n c e, s i n θ = \frac{2}{\sqrt[]{7}} . \end{array}$

If A, B, C, D are the points with position vectors î + ĵ − k̂, 2î − 3ĵ + k̂, 2î − 3k̂, and 3î + 2ĵ − k̂, respectively, find the projection of $\bar{A B}$ along $\bar{C D .}$

This is a Short Answer type Questions as classified in NCERT Exemplar

$\begin{array}{l} H e r e, P o s i t i o n v e c t o r o f A = \hat{i} + \hat{j} - \hat{k} \\ P o s i t i o n v e c t o r o f B = 2 \hat{i} - \hat{j} + 3 \hat{k} \\ P o s i t i o n v e c t o r o f C = 2 \hat{i} - 3 \hat{k} \\ P o s i t i o n v e c t o r o f D = 3 \hat{i} - 2 \hat{j} + \hat{k} \\ \vec{A B} = P . V o f B - P . V o f A \\ = (2 \hat{i} - \hat{j} + 3 \hat{k}) - (\hat{i} + \hat{j} - \hat{k}) = \hat{i} - 2 \hat{j} + 4 \hat{k} \\ \vec{C D} = P . V o f D - P . V o f C \\ = (3 \hat{i} - 2 \hat{j} + \hat{k}) - (2 \hat{i} - 3 \hat{k}) = \hat{i} - 2 \hat{j} + 4 \hat{k} \\ Projection o f \vec{A B} o n \vec{C D} = \frac{\bar{A B} \bar{. C D}}{| \bar{C D} |} = \frac{(\hat{i} - 2 \hat{j} + 4 \hat{k}) (\hat{i} - 2 \hat{j} + 4 \hat{k})}{\sqrt[]{{(1)}^{2} + {(- 2)}^{2} + {(4)}^{2}}} \\ = \frac{1 + 4 + 16}{\sqrt[]{1 + 4 + 16}} = \frac{21}{\sqrt[]{21}} = \sqrt[]{21} \\ H e n c e, t h e r e q u i r e d p rojection= \sqrt[]{21} . \end{array}$

Using vectors, find the area of the triangle ABC with vertices A(1, 2, 3), B(2, –1, 4), C(4, 5, –1).

This is a Short Answer type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n t h a t A (1, 2, 3), B (2, - 1, 4) a n d C (4, 5, - 1) \\ \vec{A B} = (2 - 1) \hat{i} + (- 1 - 2) \hat{j} + (4 - 3) \hat{k} \\ \vec{A B} = \hat{i} - 3 \hat{j} + \hat{k} \\ \vec{A C} = (4 - 1) \hat{i} + (5 - 2) \hat{j} + (- 1 - 3) \hat{k} = 3 \hat{i} + 3 \hat{j} - 4 \hat{k} \\ A r e a o f Δ A B C = \frac{1}{2} | \vec{A B} \times \vec{A C} | = \frac{1}{2} | \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & - 3 & 1 \\ 3 & 3 & - 4 \end{matrix} | \\ = \frac{1}{2} [\hat{i} (12 - 3) - \hat{j} (- 4 - 3) + \hat{k} (3 + 9)] = \frac{1}{2} | 9 \hat{i} + 7 \hat{j} + 12 \hat{k} | \\ = \frac{1}{2} \sqrt[]{{(9)}^{2} + {(7)}^{2} + {(12)}^{2}} = \frac{1}{2} \sqrt[]{81 + 49 + 144} = \frac{1}{2} \sqrt[]{274} \\ H e n c e, t h e r e q u i r e d a r e a i s \frac{\sqrt[]{274}}{2} . \end{array}$

Using vectors, prove that parallelograms on the same base and between the same parallels are equal in area.

This is a Short Answer type Questions as classified in NCERT Exemplar

$\begin{array}{l} L e t A B C D a n d A B F E b e t w o parallelograms o n t h e s a m e b a s e A B a n d b e t w e e n s a m e \\ p a r a l l e l l i n e s A B a n d D F . \\ L e t \vec{A B} = \vec{a} a n d \vec{A D} = \vec{b} \\ ∴ A r e a o f parallelogram A B C D = | \vec{a} \times \vec{b} | \\ N o w A r e a o f parallelogram A B F E = | \vec{A B} \times \vec{A E} | \\ = | \vec{a} \times (\vec{A D} + \vec{D E}) | = | \vec{a} \times (\vec{b} + K \vec{a}) | \\ = | (\vec{a} \times \vec{b}) + K (\vec{a} \times \vec{a}) | = | \vec{a} \times \vec{b} | + 0 [? \vec{a} \times \vec{a} = 0] \\ = | \vec{a} \times \vec{b} | \\ H e n c e p r o v e d . \end{array}$

Vector Algebra Long Answer Type Questions

1. Prove that in any triangle ABC, $c o s A = \frac{b^{2} + c^{2} - a^{2}}{2 b c}$ where a, b, c are the magnitudes of the sides opposite to the vertices A, B, C, respectively.

Sol:

2. If $\vec{a}, \vec{b}, \vec{c}$ determine the vertices of a triangle, show that $\frac{1}{2} (\vec{b} \times \vec{c} + \vec{c} \times \vec{a} + \vec{a} \times \vec{b})$ gives the $\vec{a}, \vec{b}, \vec{c}$ vector area of the triangle. Hence deduce the condition that the three points are collinear. Also, find the unit vector normal to the plane of the triangle.

Sol:

\begin{array}{l} Since, \vec{a}, \vec{b} a n d \vec{c} a r e t h e v e r t i c e s o f Δ A B C \\ ∴ \vec{A B} = \vec{b} - \vec{a}, \vec{B C} = \vec{c} - \vec{b} a n d \vec{A c} = \vec{c} - \vec{a} \\ ∴ A r e a o f Δ A B C = \frac{1}{2} | \vec{A B} \times \vec{A C} | \\ = \frac{1}{2} | (\vec{b} - \vec{a}) \times (\vec{c} - \vec{b}) | = \frac{1}{2} | \vec{b} \times \vec{c} - \vec{b} \times \vec{a} - \vec{a} \times \vec{c} + \vec{a} \times \vec{a} | \\ = \frac{1}{2} | \vec{b} \times \vec{c} + \vec{a} \times \vec{b} + \vec{c} \times \vec{a} | [\begin{array}{l} ∵ \vec{a} \times \vec{b} = - \vec{b} \times \vec{a} \\ \vec{c} \times \vec{a} = - \vec{a} \times \vec{c} \\ \vec{a} \times \vec{a} = \vec{0} \end{array}] \\ F o r t h r e e v e c t o r s a r e c o l l i n e a r, a r e a o f Δ A B C = 0 \\ ∴ \frac{1}{2} | \vec{b} \times \vec{c} + \vec{a} \times \vec{b} + \vec{c} \times \vec{a} | = 0 \\ | \vec{a} \times \vec{b} + \vec{b} \times \vec{c} + \vec{c} \times \vec{a} | = 0 \\ w h i c h i s t h e c o n d i t i o n o f c o l l i n e a r i t y o f \vec{a}, \vec{b} a n d \vec{c} . \\ L e t \hat{n} b e t h e u n i t v e c t o r n o r m a l t o t h e p l a n e o f t h e Δ A B C \\ ∴ \hat{n} = \frac{\vec{A B} \times \vec{A C}}{| \vec{A B} \times \vec{A C} |} = \frac{\vec{a} \times \vec{b} + \vec{b} \times \vec{c} + \vec{c} \times \vec{a}}{| \vec{a} \times \vec{b} + \vec{b} \times \vec{c} + \vec{c} \times \vec{a} |} \end{array}

Commonly asked questions

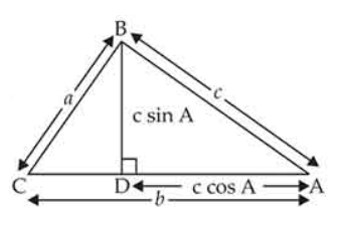
Prove that in any triangle ABC, $c o s A = \frac{b^{2} + c^{2} - a^{2}}{2 b c}$ where a, b, c are the magnitudes of the sides opposite to the vertices A, B, C, respectively.

This is a Long Answer type Questions as classified in NCERT Exemplar

Sol:

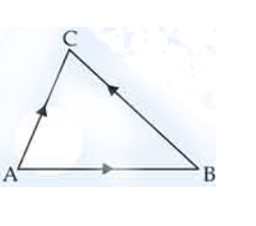
$\begin{array}{l} H e r e, i n t h e g i v e n f i g u r e, t h e c o m p o n e n t s o f c a r e c c o s A a n d a n d c s i n A . \\ ∴ \vec{C D} = b - c c o s A \\ I n Δ B D C, \\ a^{2} = C D^{2} + B D^{2} \\ \Rightarrow a^{2} = {(b - c c o s A)}^{2} + {(c s i n A)}^{2} \\ \Rightarrow a^{2} = b^{2} + c^{2} c o s^{2} A - 2 b c c o s A + c^{2} s i n^{2} A \\ \Rightarrow a^{2} = b^{2} + c^{2} (c o s^{2} A + s i n^{2} A) - 2 b c c o s A \\ \Rightarrow a^{2} = b^{2} + c^{2} - 2 b c c o s A \\ \Rightarrow 2 b c c o s A = b^{2} + c^{2} - a^{2} \\ ∴ c o s A = \frac{b^{2} + c^{2} - a^{2}}{2 b c} \\ H e n c e p r o v e d . \end{array}$

If $\vec{a}, \vec{b}, \vec{c}$ determine the vertices of a triangle, show that $\frac{1}{2} (\vec{b} \times \vec{c} + \vec{c} \times \vec{a} + \vec{a} \times \vec{b})$ gives the $\vec{a}, \vec{b}, \vec{c}$ vector area of the triangle. Hence deduce the condition that the three points are collinear. Also, find the unit vector normal to the plane of the triangle.

This is a Long Answer type Questions as classified in NCERT Exemplar

$\begin{array}{l} Since, \vec{a}, \vec{b} a n d \vec{c} a r e t h e v e r t i c e s o f Δ A B C \\ ∴ \vec{A B} = \vec{b} - \vec{a}, \vec{B C} = \vec{c} - \vec{b} a n d \vec{A c} = \vec{c} - \vec{a} \\ ∴ A r e a o f Δ A B C = \frac{1}{2} | \vec{A B} \times \vec{A C} | \\ = \frac{1}{2} | (\vec{b} - \vec{a}) \times (\vec{c} - \vec{b}) | = \frac{1}{2} | \vec{b} \times \vec{c} - \vec{b} \times \vec{a} - \vec{a} \times \vec{c} + \vec{a} \times \vec{a} | \\ = \frac{1}{2} | \vec{b} \times \vec{c} + \vec{a} \times \vec{b} + \vec{c} \times \vec{a} | [\begin{array}{l} ? \vec{a} \times \vec{b} = - \vec{b} \times \vec{a} \\ \vec{c} \times \vec{a} = - \vec{a} \times \vec{c} \\ \vec{a} \times \vec{a} = \vec{0} \end{array}] \\ F o r t h r e e v e c t o r s a r e c o l l i n e a r, a r e a o f Δ A B C = 0 \\ ∴ \frac{1}{2} | \vec{b} \times \vec{c} + \vec{a} \times \vec{b} + \vec{c} \times \vec{a} | = 0 \\ | \vec{a} \times \vec{b} + \vec{b} \times \vec{c} + \vec{c} \times \vec{a} | = 0 \\ w h i c h i s t h e c o n d i t i o n o f c o l l i n e a r i t y o f \vec{a}, \vec{b} a n d \vec{c} . \\ L e t \hat{n} b e t h e u n i t v e c t o r n o r m a l t o t h e p l a n e o f t h e Δ A B C \\ ∴ \hat{n} = \frac{\vec{A B} \times \vec{A C}}{| \vec{A B} \times \vec{A C} |} = \frac{\vec{a} \times \vec{b} + \vec{b} \times \vec{c} + \vec{c} \times \vec{a}}{| \vec{a} \times \vec{b} + \vec{b} \times \vec{c} + \vec{c} \times \vec{a} |} \end{array}$

Show that the area of the parallelogram whose diagonals are given by $\vec{a}$ and $\vec{b}$ is $\frac{1}{2} ∣ \frac{\vec{a} \times \vec{b}}{2} ∣$ Also, find the area of the parallelogram whose diagonals are 2î − ĵ + k̂ and î + 3ĵ − k̂.

This is a Long Answer type Questions as classified in NCERT Exemplar

\begin{array}{l} L e t A B C D b e a parallelogram s u c h t h a t, \\ \vec{A B} = \vec{p}, \vec{A D} = \vec{q} = \vec{B C} \\ ∴ b y l a w o f t r i a n g l e, w e g e t \\ \vec{A C} = \vec{a} = \vec{p} + \vec{q} \dots (i) \\ a n d \vec{B D} = \vec{b} = - \vec{p} + \vec{q} \dots (i i) \\ A d d i n g e q . (i) a n d (i i) w e g e t, \\ \vec{a} + \vec{b} = 2 \vec{q} \Rightarrow \vec{q} = (\frac{\vec{a} + \vec{b}}{2}) \\ S u b t r a c t i n g e q . (i i) f r o m (i) w e g e t, \\ \vec{a} - \vec{b} = 2 \vec{p} \Rightarrow \vec{p} = (\frac{\vec{a} - \vec{b}}{2}) \\ ∴ \vec{p} \times \vec{q} = \frac{1}{4} (\vec{a} + \vec{b}) (\vec{a} - \vec{b}) = \frac{1}{4} (\vec{a} \times \vec{a} - \vec{a} \times \vec{b} + \vec{b} \times \vec{a} - \vec{b} \times \vec{b}) \\ = \frac{1}{4} (- \vec{a} \times \vec{b} + \vec{b} \times \vec{a}) [\begin{array}{l} ? \vec{a} \times \vec{a} = 0 \\ \vec{b} \times \vec{b} = 0 \end{array}] \\ = \frac{1}{4} (\vec{a} \times \vec{b} + \vec{b} \times \vec{a}) = \frac{1}{4} . 2 (\vec{a} \times \vec{b}) = \frac{| \vec{a} \times \vec{b} |}{2} \\ S o, t h e a r e a o f parallelogram A B C D = | \vec{p} \times \vec{q} | = \frac{1}{2} | \vec{a} \times \vec{b} | \\ N o w a r e a o f parallelogram w h o s e d i a g o n a l s a r e 2 \hat{i} - \hat{j} + \hat{k} a n d \hat{i} + 3 \hat{j} - \hat{k} \\ = \frac{1}{2} | (2 \hat{i} - \hat{j} + \hat{k}) \times (\hat{i} + 3 \hat{j} - \hat{k}) | \\ = \frac{1}{2} | \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & - 1 & 1 \\ 1 & 3 & - 1 \end{matrix} | \\ = \frac{1}{2} [\hat{i} (1 - 3) - \hat{j} (- 2 - 1) + \hat{k} (6 + 1)] = \frac{1}{2} | - 2 \hat{i} + 3 \hat{j} + 7 \hat{k} | \\ = \frac{1}{2} \sqrt[]{{(- 2)}^{2} + {(3)}^{2} + {(7)}^{2}} = \frac{1}{2} \sqrt[]{4 + 9 + 49} = \frac{1}{2} \sqrt[]{62} s q . u n i t s . \\ H e n c e, t h e r e q u i r e d a r e a i s \frac{1}{2} \sqrt[]{62} s q . u n i t s . \end{array}

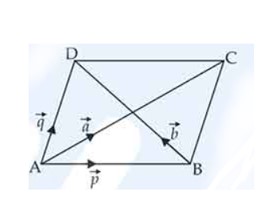
If $\vec{a}$ = î + ĵ + k̂ and b̂ = ĵ − k̂, find a vector $c$ such that $\vec{a} \times \vec{c}$ = $\vec{b}$ and $\vec{a} . \vec{c}$ = 3.

This is a Long Answer type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} L e t \vec{c} = c_{1} \hat{i} + c_{2} \hat{j} + c_{3} \hat{k} \\ A l s o g i v e n t h a t \vec{a} = \hat{i} + \hat{j} + \hat{k} a n d \vec{b} = \hat{j} - \hat{k} \\ S i n c e, \vec{a} \times \vec{c} = \vec{b} \\ ∴ | \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & 1 & 1 \\ c_{1} & c_{2} & c_{3} \end{matrix} | = \hat{j} - \hat{k} \\ \hat{i} (c_{3} - c_{2}) - \hat{j} (c_{3} - c_{1}) + \hat{k} (c_{2} - c_{1}) = \hat{j} - \hat{k} \\ O n c o m p a r i n g t h e l i k e t e r m s, w e g e t \\ c_{3} - c_{2} = 0 \dots (i) \\ c_{1} - c_{3} = 1 \dots (i i) \\ c_{2} - c_{1} = - 1 \dots (i i i) \\ N o w f o r \vec{a} . \vec{c} = 3 \\ (\hat{i} + \hat{j} + \hat{k}) . (c_{1} \hat{i} + c_{2} \hat{j} + c_{3} \hat{k}) = 3 \\ ∴ c_{1} + c_{2} + c_{3} = 3 \dots (i v) \\ A d d i n g e q . (i i) a n d e q . (i i i) w e g e t, \\ c_{2} - c_{3} = 0 \dots (v) \\ F r o m (i v) a n d (v) w e g e t \\ c_{1} + 2 c_{2} = 3 \dots (v i) \\ F r o m (i i i) a n d (v i) w e g e t \\ c_{1} + 2 c_{2} = 3 \\ \underline{- c_{1} + c_{2} = - 1} \\ A d d i n g 3 c_{2} = 2 \\ ∴ c_{2} = \frac{2}{3} \\ c_{3} - c_{2} = 0 \Rightarrow c_{3} - \frac{2}{3} = 0 ∴ c_{3} = \frac{2}{3} \\ N o w, c_{2} - c_{1} = - 1 \Rightarrow \frac{2}{3} - c_{1} = - 1 \\ \Rightarrow c_{1} = 1 + \frac{2}{3} = \frac{5}{3} \\ ∴ \vec{c} = \frac{5}{3} \hat{i} + \frac{2}{3} \hat{j} + \frac{2}{3} \hat{k} = \frac{1}{3} (5 \hat{i} + 2 \hat{j} + 2 \hat{k}) \\ H e n c e, \vec{c} = \frac{1}{3} (5 \hat{i} + 2 \hat{j} + 2 \hat{k}) . \end{array}$

Vector Algebra Objective Type Questions

Choose the correct answer from the given four options in each of the Exercises 19 to 33:

1. The vector in the direction of the vector î − 2ĵ + 2k̂ that has magnitude 9 is:

(A) î − 2ĵ + 2k̂

(B) $\frac{(\hat{i} - 2 \hat{j} + 2 \hat{k})}{3}$

(C) 9(î − 2ĵ + 2k̂)

(D) (î − 2ĵ + 2k̂)/3

Sol:

$\begin{array}{l} L e t \vec{a} = \hat{i} - 2 \hat{j} + 2 \hat{k} \\ U n i t v e c t o r i n t h e d i r e c t i o n o f \vec{a} = \frac{\vec{a}}{| \vec{a} |} \\ = \frac{\hat{i} - 2 \hat{j} + 2 \hat{k}}{\sqrt[]{{(1)}^{2} + {(- 2)}^{2} + {(2)}^{2}}} = \frac{\hat{i} - 2 \hat{j} + 2 \hat{k}}{\sqrt[]{1 + 4 + 4}} = \frac{\hat{i} - 2 \hat{j} + 2 \hat{k}}{3} \\ ∴ v e c t o r o f m a g n i t u d e 9 = \frac{9 (\hat{i} - 2 \hat{j} + 2 \hat{k})}{3} = 3 (\hat{i} - 2 \hat{j} + 2 \hat{k}) \\ H e n c e, t h e c o r r e c t o p t i o n i s (c) . \end{array}$

2. The position vector of the point that divides the join of points 2â − 3b̂ and â + b̂ in the ratio 3:1 is:

(A) $\frac{(3 \vec{a} - 2 \hat{\vec{b}})}{2}$

(B) $\frac{(7 \vec{a} - 8 \hat{\vec{b}})}{4}$

(C) $\frac{3 \vec{a}}{4}$

(D) $\frac{5 \vec{a}}{4}$

Sol:

$\begin{array}{l} T h e g i v e n v e c t o r s a r e 2 \vec{a} - 3 \vec{b} a n d \vec{a} + \vec{b} a n d t h e r a t i o i s 3 : 1 . \\ ∴ T h e p o s i t i o n v e c t o r o f t h e r e q u i r e d point c w h i c h d i v i d e s t h e j o i n o f t h e g i v e n \\ v e c t o r s \vec{a} a n d \vec{b} i s \\ \vec{c} = \frac{m_{1} x_{2} + m_{2} x_{1}}{m_{1} + m_{2}} = \frac{1 . (2 \vec{a} - 3 \vec{b}) + 3 (\vec{a} + \vec{b})}{3 + 1} = \frac{2 \vec{a} - 3 \vec{b} + 3 \vec{a} + 3 \vec{b}}{4} \\ = \frac{5 \vec{a}}{4} = \frac{5}{4} \vec{a} \\ H e n c e, t h e c o r r e c t o p t i o n i s (d) . \end{array}$

Commonly asked questions

Choose the correct answer from the given four options in each of the Exercises 19 to 33:

The vector in the direction of the vector î − 2? + 2k? that has magnitude 9 is:

(A) î − 2ĵ + 2k̂

(B) $\frac{(\hat{i} - 2 \hat{j} + 2 \hat{k})}{3}$

(C) 9(î − 2ĵ + 2k̂)

(D) (î − 2ĵ + 2k̂)/3

This is a Objective type Questions as classified in NCERT Exemplar

Sol:

The position vector of the point that divides the join of points 2â − 3b̂ and â + b̂ in the ratio 3:1 is:

(A) $\frac{(3 \vec{a} - 2 \hat{\vec{b}})}{2}$

(B) $\frac{(7 \vec{a} - 8 \hat{\vec{b}})}{4}$

(C) ^{$\frac{3 \vec{a}}{4}$}

(D) $\frac{5 \vec{a}}{4}$

This is an Objective type Questions as classified in NCERT Exemplar

Sol:

The vector having initial and terminal points as (2, 5, 0) and (–3, 7, 4), respectively, is

(A) –î + 12ĵ + 4k̂

(B) 5î − 2ĵ − 4k̂

(C) −5î + 2ĵ + 4k̂

(D) î + ĵ + k̂

This is a Objective type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} L e t A a n d B b e t w o points w h o s e c o o r d i n a t e s a r e g i v e n a s (2, 5, 0) a n d (- 3, 7, 4) \\ ∴ \vec{A B} = (- 3 - 2) \hat{i} + (7 - 5) \hat{j} + (4 - 0) \hat{k} \\ \Rightarrow \vec{A B} = - 5 \hat{i} + 2 \hat{j} + 4 \hat{k} \\ H e n c e, t h e c o r r e c t o p t i o n i s (c) . \end{array}$

The angle between two vectors $\vec{a}$ , $\vec{b}$ with magnitudes √3 and 4, respectively, and $\vec{a}$ . $\vec{b}$ = 2√3 is:

(A) $\frac{π}{6}$

(B) $\frac{π}{3}$

(C) $\frac{π}{2}$

(D) $\frac{5 π}{2}$

This is a Objective type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} H e r e, g i v e n t h a t | \vec{a} | = \sqrt[]{3}, | \vec{b} | = 4 a n d \vec{a} . \vec{b} = 2 \sqrt[]{3} \\ ∴ F r o m s c a l a r p r o d u c t, w e k n o w t h a t \\ \vec{a} . \vec{b} = | \vec{a} | | \vec{b} | c o s θ \\ \Rightarrow 2 \sqrt[]{3} = \sqrt[]{3} . 4 . c o s θ \\ \Rightarrow c o s θ = \frac{2 \sqrt[]{3}}{\sqrt[]{3} . 4} = \frac{1}{2} \\ ∴ θ = \frac{π}{3} \\ H e n c e, t h e c o r r e c t o p t i o n i s (b) . \end{array}$

Find the value of λ such that the vectors $\vec{a}$ = 2î + λĵ + k̂ and $\vec{b}$ = î + 2ĵ + 3k̂ are orthogonal.

(A) 0

(B) 1

(C) $\frac{3}{2}$

(D) − $\frac{5}{2}$

This is an Objective type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n t h a t \vec{a} = 2 \hat{i} + λ \hat{j} + \hat{k} a n d \vec{b} = \hat{i} + 2 \hat{j} + 3 \hat{k} \\ Since \vec{a} a n d \vec{b} a r e o r t h o g o n a l \\ ∴ \vec{a} . \vec{b} = 0 \\ \Rightarrow (2 \hat{i} + λ \hat{j} + \hat{k}) . (\hat{i} + 2 \hat{j} + 3 \hat{k}) = 0 \\ \Rightarrow 2 + 2 λ + 3 = 0 \\ \Rightarrow 5 + 2 λ = 0 \Rightarrow λ = \frac{- 5}{2} \\ H e n c e, t h e c o r r e c t o p t i o n i s (d) . \end{array}$

The value of λ for which the vectors 3î − 6? + k? and 2î − 4? + λk? are parallel is:

(A) $\frac{2}{3}$

(B) $\frac{3}{2}$

(C) $\frac{5}{2}$

(D) $\frac{2}{5}$

This is an Objective type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} L e t \vec{a} = a_{1} \hat{i} + a_{2} \hat{j} + a_{3} \hat{k} a n d \vec{b} = b_{1} \hat{i} + b_{2} \hat{j} + b_{3} \hat{k} \\ I f \vec{a} ? \vec{b} \\ ∴ \frac{a_{1}}{b_{1}} = \frac{a_{2}}{b_{2}} = \frac{a_{3}}{b_{3}} \\ \Rightarrow \frac{3}{2} = \frac{- 6}{- 4} = \frac{1}{λ} \Rightarrow \frac{1}{λ} = \frac{3}{2} \Rightarrow λ = \frac{2}{3} \\ H e n c e, t h e c o r r e c t o p t i o n i s (a) . \end{array}$

The vectors from the origin to the points A and B are: respectively. Then the area of triangle OAB is:

(A) 340

(B) 25

(D) $\frac{1}{2} \sqrt[]{229}$

This is an Objective type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} L e t O b e t h e o r i g i n \\ ∴ \vec{O A} = 2 \hat{i} - 3 \hat{j} + 2 \hat{k} a n d \vec{O B} = 2 \hat{i} - 3 \hat{j} + 2 \hat{k} \\ ∴ A r e a o f Δ O A B = \frac{1}{2} | \vec{O A} \times \vec{O B} | = \frac{1}{2} | \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & - 3 & 2 \\ 2 & 3 & 1 \end{matrix} | \\ = \frac{1}{2} | \hat{i} (- 3 - 6) - \hat{j} (2 - 4) + \hat{k} (6 + 6) | \\ = \frac{1}{2} | - 9 \hat{i} + 2 \hat{j} + 12 \hat{k} | = \frac{1}{2} \sqrt[]{{(- 9)}^{2} + {(2)}^{2} + {(12)}^{2}} \\ = \frac{1}{2} \sqrt[]{81 + 4 + 144} = \frac{1}{2} \sqrt[]{229} \\ H e n c e, t h e c o r r e c t o p t i o n i s (d) . \end{array}$

For any vector , the value of is equal to:

(A) ${\vec{a}}^{2}$

(B) $3 {\vec{a}}^{2}$

(C) $4 {\vec{a}}^{2}$

(D) $2 {\vec{a}}^{2}$

This is an Objective type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} L e t \vec{a} = a_{1} \hat{i} + a_{2} \hat{j} + a_{3} \hat{k} \\ ∴ {\vec{a}}^{2} = a_{1}^{2} + a_{2}^{2} + a_{3}^{2} \\ N o w, \vec{a} \times \hat{i} = (a_{1} \hat{i} + a_{2} \hat{j} + a_{3} \hat{k}) \times \hat{i} \\ = | \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ a_{1} & a_{2} & a_{3} \\ 1 & 0 & 0 \end{matrix} | \\ = \hat{i} (0 - 0) - \hat{j} (0 - a_{3}) + \hat{k} (0 - a_{2}) = a_{3} \hat{j} - a_{2} \hat{k} \\ ∴ {(\vec{a} \times \hat{i})}^{2} = (a_{3} \hat{j} - a_{2} \hat{k}) . (a_{3} \hat{j} - a_{2} \hat{k}) = a_{3}^{2} + a_{2}^{2} \\ S i m i l a r l y {(\vec{a} \times \hat{j})}^{2} = a_{1}^{2} + a_{3}^{2} a n d {(\vec{a} \times \hat{k})}^{2} = a_{1}^{2} + a_{2}^{2} \\ ∴ {(\vec{a} \times \hat{i})}^{2} + {(\vec{a} \times \hat{j})}^{2} + {(\vec{a} \times \hat{k})}^{2} = a_{3}^{2} + a_{2}^{2} + a_{1}^{2} + a_{3}^{2} + a_{1}^{2} + a_{2}^{2} \\ = 2 (a_{1}^{2} + a_{2}^{2} + a_{3}^{2}) = 2 {\vec{a}}^{2} \\ H e n c e, t h e c o r r e c t o p t i o n i s (d) . \end{array}$

If $∣ \vec{a} ∣ = 10$ , $∣ \vec{b} ∣ = 2$ , and $\vec{a} \cdot \vec{b} = 12$ , then the value of $∣ \vec{a} \times \vec{b} ∣$ is:

(A) 5

(B) 10

(C) 14

(D) 16

This is an Objective type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n t h a t \vec{a} = 10, \vec{b} = 2 a n d \vec{a} . \vec{b} = 12 \\ ∴ \vec{a} . \vec{b} = | \vec{a} | | \vec{b} | c o s θ \\ \Rightarrow 12 = 10 . 2 . c o s θ \\ \Rightarrow c o s θ = \frac{12}{20} = \frac{3}{5} \\ ∴ s i n θ = \sqrt[]{1 - c o s^{2} θ} \\ \Rightarrow s i n θ = \sqrt[]{1 - {(\frac{3}{5})}^{2}} \Rightarrow s i n θ = \sqrt[]{1 - \frac{9}{25}} \\ \Rightarrow s i n θ = \sqrt[]{\frac{16}{25}} \Rightarrow s i n θ = \frac{4}{5} \\ N o w | \vec{a} \times \vec{b} | = | \vec{a} | | \vec{b} | s i n θ \\ = 10 . 2 . \frac{4}{5} = 16 \\ H e n c e, t h e c o r r e c t o p t i o n i s (d) . \end{array}$

The vectors $λ \hat{i} + \hat{j} + 2 \hat{k}, \hat{i} + λ \hat{j} - \hat{k}, a n d 2 \hat{i} + \hat{j} + λ \hat{k}$ are coplanar if:

(A) $λ = - 2$

(B) $λ = 0$

(C) $λ = 1$

(D) $λ = - 1$

This is an Objective type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} L e t \vec{a} = λ \hat{i} + \hat{j} + 2 \hat{k} \\ ∴ \vec{b} = \hat{i} + λ \hat{j} - \hat{k} \\ \vec{c} = 2 \hat{i} - \hat{j} + λ \hat{k} \\ I f \vec{a}, \vec{b} a n d \vec{c} a r e c o p l a n a r, t h e n \\ \vec{a} . (\vec{b} \times \vec{c}) = 0 \\ ∴ | \begin{matrix} λ & 1 & 2 \\ 1 & λ & - 1 \\ 2 & - 1 & λ \end{matrix} | = 0 \\ \Rightarrow λ (λ^{2} - 1) - 1 (λ + 2) + 2 (- 1 - 2 λ) = 0 \\ \Rightarrow λ^{3} - λ - λ - 2 - 2 - 4 λ = 0 \\ \Rightarrow λ^{3} - 6 λ - 4 = 0 \\ \Rightarrow (λ + 2) (λ^{2} - 2 λ - 2) = 0 \\ \Rightarrow λ = - 2 o r λ^{2} - 2 λ - 2 = 0 \\ \Rightarrow λ = \frac{2 \pm \sqrt[]{4 + 8}}{2} \\ \Rightarrow λ = \frac{2 \pm 2 \sqrt[]{3}}{2} \\ ∴ λ = - 2 o r 1 \pm \sqrt[]{3} \\ H e n c e, t h e c o r r e c t o p t i o n i s (a) . \end{array}$

If $\vec{a}, \vec{b}, \vec{c}$ are unit vectors such that $\vec{a} + \vec{b} + \vec{c} = 0$ then the value of $\vec{a .} \vec{b} + \vec{b} . \vec{c} + \vec{c} . \vec{a}$ is:

(A) 1

(B) 3

(C) $- \frac{3}{2}$

(D) None of these

This is an Objective type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n t h a t | \vec{a} | = | \vec{b} | = | \vec{c} | = 1 \\ a n d \vec{a} + \vec{b} + \vec{c} = \vec{0} \\ ∴ (\vec{a} + \vec{b} + \vec{c}) . (\vec{a} + \vec{b} + \vec{c}) = \vec{0} . \vec{0} = 0 \\ {| \vec{a} |}^{2} + \vec{a} . \vec{b} + \vec{a} . \vec{c} + \vec{b} . \vec{a} + {| \vec{b} |}^{2} + \vec{b} . \vec{c} + \vec{c} . \vec{a} + \vec{c} . \vec{b} + {| \vec{c} |}^{2} = 0 \\ \Rightarrow {| \vec{a} |}^{2} + {| \vec{b} |}^{2} + {| \vec{c} |}^{2} + 2 \vec{a} . \vec{b} + 2 \vec{b} . \vec{c} + 2 \vec{c} . \vec{a} = 0 \\ \Rightarrow 1 + 1 + 1 + 2 (\vec{a} . \vec{b} + \vec{b} . \vec{c} + \vec{c} . \vec{a}) = 0 \\ \Rightarrow 2 (\vec{a} . \vec{b} + \vec{b} . \vec{c} + \vec{c} . \vec{a}) = - 3 \\ \Rightarrow \vec{a} . \vec{b} + \vec{b} . \vec{c} + \vec{c} . \vec{a} = \frac{- 3}{2} \\ H e n c e, t h e c o r r e c t o p t i o n i s (c) . \end{array}$

The projection vector of $\vec{a .}$ on $\vec{b}$ is:

(A) $\frac{(\vec{a .} \cdot \vec{b})}{∣ \vec{b} ∣^{2}} \vec{b}$

(B) $\frac{\vec{a .} \cdot \vec{b}}{∣ \vec{b} ∣} \vec{b}$

(C) $\frac{(\vec{a .} \cdot \vec{b})}{∣ \vec{a .} ∣}$

(D) $\frac{(\vec{a} \cdot \vec{b})}{∣ \vec{a} ∣^{2}} \vec{b}$

This is an Objective type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e p r o j e c t i o n v e c t o r o f \vec{a} o n \vec{b} = (\frac{\vec{a} . \vec{b}}{| \vec{b} |}) . \vec{b} \\ H e n c e, t h e c o r r e c t o p t i o n i s (a) . \end{array}$

If $\vec{a}, \vec{b}, \vec{c}$ are three vectors such that $\vec{a} + \vec{b} + \vec{c} = 0$ and $? \vec{a} | = 2$ , $? \vec{b} | = 2, ? \vec{c} | = 2$ then the value of $\vec{a .} \vec{b} + \vec{b} . \vec{c} + \vec{c} . \vec{a}$ is:

(A) 0

(B) 1

(C) $- 19$

(D) 38

This is an Objective type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n t h a t | \vec{a} | = 2, | \vec{b} | = 3, | \vec{c} | = 5 \\ a n d \vec{a} + \vec{b} + \vec{c} = \vec{0} \\ ∴ (\vec{a} + \vec{b} + \vec{c}) . (\vec{a} + \vec{b} + \vec{c}) = \vec{0} . \vec{0} = 0 \\ {| \vec{a} |}^{2} + \vec{a} . \vec{b} + \vec{a} . \vec{c} + \vec{b} . \vec{a} + {| \vec{b} |}^{2} + \vec{b} . \vec{c} + \vec{c} . \vec{a} + \vec{c} . \vec{b} + {| \vec{c} |}^{2} = 0 \\ \Rightarrow {| \vec{a} |}^{2} + {| \vec{b} |}^{2} + {| \vec{c} |}^{2} + 2 \vec{a} . \vec{b} + 2 \vec{b} . \vec{c} + 2 \vec{c} . \vec{a} = 0 \\ \Rightarrow {(2)}^{2} + {(3)}^{2} + {(5)}^{2} + 2 (\vec{a} . \vec{b} + \vec{b} . \vec{c} + \vec{c} . \vec{a}) = 0 \\ \Rightarrow 4 + 9 + 25 + 2 (\vec{a} . \vec{b} + \vec{b} . \vec{c} + \vec{c} . \vec{a}) = 0 \\ \Rightarrow 38 + 2 (\vec{a} . \vec{b} + \vec{b} . \vec{c} + \vec{c} . \vec{a}) = 0 \\ \Rightarrow 2 (\vec{a} . \vec{b} + \vec{b} . \vec{c} + \vec{c} . \vec{a}) = - 38 \\ \Rightarrow \vec{a} . \vec{b} + \vec{b} . \vec{c} + \vec{c} . \vec{a} = - 19 \\ H e n c e, t h e c o r r e c t o p t i o n i s (c) . \end{array}$

If $∣ \vec{a} ∣ = 4$ and $- 3 \leq λ \leq 2$ , then the range of $∣ λ \vec{a} ∣$ is:

(A) [0, 8]

(B) [-12, 8]

(C) [0, 12]

(D) [8, 12]

This is an Objective type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n t h a t | \vec{a} | = 4, - 3 \leq λ \leq 2 \\ N o w | λ \vec{a} | = λ | \vec{a} | = λ . 4 = 4 λ \\ H e r e, - 3 \leq λ \leq 2 \\ \Rightarrow - 3.4 \leq 4 λ \leq 2.4 \Rightarrow - 12 \leq 4 λ \leq 8 \\ ∴ 4 λ = [- 12, 8] \\ H e n c e, t h e c o r r e c t o p t i o n i s (b) . \end{array}$

The number of unit vectors perpendicular to both $\vec{a} = 2 \hat{i} + 2 \hat{j} + \hat{k}, \vec{b} = \hat{j} + 2 \hat{k}$ is:

(A) One

(B) Two

(C) Three

(D) Infinite

This is an Objective type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e n u m b e r o f v e c t o r s o f u n i t l e n g t h p e r p e n d i c u l a r t o v e c t o r s \vec{a} a n d \vec{b} i s \vec{c} (L e t) \\ ∴ \vec{c} = \pm (\vec{a} \times \vec{b}) \\ S o, t h e r e w i l l b e t w o v e c t o r s o f u n i t l e n g t h p e r p e n d i c u l a r t o v e c t o r s \vec{a} a n d \vec{b} . \\ H e n c e, t h e c o r r e c t o p t i o n i s (b) . \end{array}$

Vector Algebra Fill in the blanks

1. The vector $\vec{a}$ + $\vec{b}$ bisects the angle between the non-collinear vectors $\vec{a}$ and $\vec{b}$ if ________.

Sol:

$\begin{array}{l} I f v e c t o r \vec{a} + \vec{b} bisects t h e a n g l e b e t w e e n n o n - c o l l i n e a r v e c t o r s \vec{a} a n d \vec{b} t h e n t h e a n g l e b e t w e e n \\ \vec{a} + \vec{b} a n d \vec{a} i s e q u a l t o t h e a n g l e b e t w e e n \vec{a} + \vec{b} a n d \vec{b} . \\ S o, c o s θ = \frac{\vec{a} . (\vec{a} + \vec{b})}{| \vec{a} | | \vec{a} + \vec{b} |} = \frac{\vec{a} . (\vec{a} + \vec{b})}{| \vec{a} | \sqrt[]{a^{2} + b^{2}}} \dots (i) \\ A l s o, c o s θ = \frac{\vec{b} . (\vec{a} + \vec{b})}{| \vec{b} | | \vec{a} + \vec{b} |} [∵ θ i s s a m e] \\ = \frac{\vec{b} . (\vec{a} + \vec{b})}{| \vec{b} | \sqrt[]{a^{2} + b^{2}}} \dots (i i) \\ F r o m e q . (i) a n d e q . (i i) w e g e t, \\ \frac{\vec{a} . (\vec{a} + \vec{b})}{| \vec{a} | \sqrt[]{a^{2} + b^{2}}} = \frac{\vec{b} . (\vec{a} + \vec{b})}{| \vec{b} | \sqrt[]{a^{2} + b^{2}}} \\ \Rightarrow \frac{\vec{a}}{| \vec{a} |} = \frac{\vec{b}}{| \vec{b} |} \\ \Rightarrow \hat{a} = \hat{b} \Rightarrow \vec{a} = \vec{b} \\ H e n c e, t h e r e q u i r e d f i l l e r i s \vec{a} = \vec{b} . \end{array}$

2. If $\vec{r}$ . $\vec{a}$ = 0, $\vec{r}$ . $\vec{b}$ = 0, $\vec{r}$ . $\vec{c}$ = 0 for some non-zero vector r̂, then the value of (

\vec{a}

× $\vec{b}$ ) ĉ is ________.

Sol:

$\begin{array}{l} I f \vec{r} i s a n o n - z e r o v e c t o r, t h e n \vec{a}, \vec{b} a n d \vec{c} c a n b e i n t h e s a m e p l a n e . \\ Since a n g l e s b e t w e e n \vec{a}, \vec{b} a n d \vec{c} a r e z e r o i . e . θ = 0 \\ ∴ \vec{a} . (\vec{b} \times \vec{c}) = 0 \\ H e n c e, t h e r e q u i r e d v a l u e i s 0 . \end{array}$

Commonly asked questions

The vector $\vec{a}$ + $\vec{b}$ bisects the angle between the non-collinear vectors $\vec{a}$ and $\vec{b}$ if ________.

This is a Fill in the blanks type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} I f v e c t o r \vec{a} + \vec{b} bisects t h e a n g l e b e t w e e n n o n - c o l l i n e a r v e c t o r s \vec{a} a n d \vec{b} t h e n t h e a n g l e b e t w e e n \\ \vec{a} + \vec{b} a n d \vec{a} i s e q u a l t o t h e a n g l e b e t w e e n \vec{a} + \vec{b} a n d \vec{b} . \\ S o, c o s θ = \frac{\vec{a} . (\vec{a} + \vec{b})}{| \vec{a} | | \vec{a} + \vec{b} |} = \frac{\vec{a} . (\vec{a} + \vec{b})}{| \vec{a} | \sqrt[]{a^{2} + b^{2}}} \dots (i) \\ A l s o, c o s θ = \frac{\vec{b} . (\vec{a} + \vec{b})}{| \vec{b} | | \vec{a} + \vec{b} |} [? θ i s s a m e] \\ = \frac{\vec{b} . (\vec{a} + \vec{b})}{| \vec{b} | \sqrt[]{a^{2} + b^{2}}} \dots (i i) \\ F r o m e q . (i) a n d e q . (i i) w e g e t, \\ \frac{\vec{a} . (\vec{a} + \vec{b})}{| \vec{a} | \sqrt[]{a^{2} + b^{2}}} = \frac{\vec{b} . (\vec{a} + \vec{b})}{| \vec{b} | \sqrt[]{a^{2} + b^{2}}} \\ \Rightarrow \frac{\vec{a}}{| \vec{a} |} = \frac{\vec{b}}{| \vec{b} |} \\ \Rightarrow \hat{a} = \hat{b} \Rightarrow \vec{a} = \vec{b} \\ H e n c e, t h e r e q u i r e d f i l l e r i s \vec{a} = \vec{b} . \end{array}$

If $\vec{r}$ . $\vec{a}$ = 0, $\vec{r}$ . $\vec{b}$ = 0, $\vec{r}$ . $\vec{c}$ = 0 for some non-zero vector r̂, then the value of
( $\vec{a}$ × $\vec{b}$ ) ĉ is ________.

This is a Fill in the blanks type Questions as classified in NCERT Exemplar

Sol:

The vectors $\vec{a}$ = 3î − 2ĵ + 2k̂ and b̂ = î − 2k̂ are the adjacent sides of a parallelogram. The acute angle between its diagonals is ________.

This is a Fill in the blanks type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n t h a t \vec{a} = 3 \hat{i} - 2 \hat{j} + 2 \hat{k} \\ a n d \vec{b} = - \hat{i} - 2 \hat{k} \\ ∴ \vec{a} + \vec{b} = 2 \hat{i} - 2 \hat{j} a n d \vec{a} - \vec{b} = 4 \hat{i} - 2 \hat{j} + 4 \hat{k} \\ L e t θ b e t h e a n g l e b e t w e e n t h e t w o d i a g o n a l v e c t o r s \vec{a} + \vec{b} a n d \vec{a} - \vec{b} t h e n \\ c o s θ = \frac{(\vec{a} + \vec{b}) . (\vec{a} - \vec{b})}{| \vec{a} + \vec{b} | | \vec{a} - \vec{b} |} = \frac{(2 \hat{i} - 2 \hat{j}) . (4 \hat{i} - 2 \hat{j} + 4 \hat{k})}{\sqrt[]{{(2)}^{2} + {(- 2)}^{2}} \sqrt[]{{(4)}^{2} + {(- 2)}^{2} + {(4)}^{2}}} \\ = \frac{8 + 4}{2 \sqrt[]{2} . 6} = \frac{12}{2 \sqrt[]{2} . 6} = \frac{1}{\sqrt[]{2}} \\ ∴ θ = \frac{π}{4} \\ H e n c e, t h e v a l u e o f r e q u i r e d f i l l e r i s \frac{π}{4} . \end{array}$

The values of k for which |k $\vec{a}$ <| $\vec{a |}$ | and k $\vec{a} + \frac{1}{2} \vec{a}$ is parallel to $\vec{a}$ holds true are ________.

This is a Fill in the blanks type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n t h a t | k \vec{a} | < | \vec{a} | a n d k \vec{a} + \frac{1}{2} \vec{a} i s p a r a l l e l t o \vec{a} \\ ∴ | k \vec{a} | < | \vec{a} | \Rightarrow | k | | \vec{a} | < | \vec{a} | \Rightarrow | k | < 1 \Rightarrow - 1 < k < 1 \\ N o w since k \vec{a} + \frac{1}{2} \vec{a} i s p a r a l l e l t o \vec{a} \\ H e r e, w e s e e t h a t k = - \frac{1}{2}, k \vec{a} + \frac{1}{2} \vec{a} b e c o m e n u l l v e c t o r a n d t h e n i t w i l l n o t b e p a r a l l e l t o \vec{a} . \\ ∴ k \vec{a} + \frac{1}{2} \vec{a} i s p a r a l l e l t o \vec{a} w h e n k \in (- 1, 1) a n d k \neq \frac{1}{2} . \\ H e n c e, t h e r e q u i r e d v a l u e o f k \in (- 1, 1) a n d k \neq \frac{1}{2} . \end{array}$

The value of the expression $(\vec{a} \times b ?)^{2}$ + ${(\vec{a} . \vec{b})}^{2}$ is ________.

This is a Fill in the blanks type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} {| \vec{a} \times \vec{b} |}^{2} + {(\vec{a} . \vec{b})}^{2} = {(| \vec{a} | | \vec{b} | s i n θ)}^{2} + {(| \vec{a} | | \vec{b} | c o s θ)}^{2} \\ = {| \vec{a} |}^{2} {| \vec{b} |}^{2} s i n^{2} θ + {| \vec{a} |}^{2} {| \vec{b} |}^{2} c o s^{2} θ \\ = {| \vec{a} |}^{2} {| \vec{b} |}^{2} . (s i n^{2} θ + c o s^{2} θ) \\ = {| \vec{a} |}^{2} {| \vec{b} |}^{2} . 1 = {| \vec{a} |}^{2} {| \vec{b} |}^{2} \\ H e n c e, t h e v a l u e o f t h e f i l l e r i s {| \vec{a} |}^{2} {| \vec{b} |}^{2} . \end{array}$

If $\vec{| a} . \times \vec{b} |^{2} + \vec{| a} . \vec{b} |^{2} = 144 a n d \vec{| a} | = 4,$ then b is equal to _______.

This is a Fill in the blanks type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} {| \vec{a} \times \vec{b} |}^{2} + {(\vec{a} . \vec{b})}^{2} = 144 \\ \Rightarrow {(| \vec{a} | | \vec{b} | s i n θ)}^{2} + {(| \vec{a} | | \vec{b} | c o s θ)}^{2} = 144 \\ \Rightarrow {| \vec{a} |}^{2} {| \vec{b} |}^{2} s i n^{2} θ + {| \vec{a} |}^{2} {| \vec{b} |}^{2} c o s^{2} θ = 144 \\ \Rightarrow {| \vec{a} |}^{2} {| \vec{b} |}^{2} . (s i n^{2} θ + c o s^{2} θ) = 144 \\ \Rightarrow {| \vec{a} |}^{2} {| \vec{b} |}^{2} = 144 \\ \Rightarrow | \vec{a} | | \vec{b} | = 12 \\ \Rightarrow 4 . | \vec{b} | = 12 \\ ∴ | \vec{b} | = 3 \\ H e n c e, t h e v a l u e o f t h e f i l l e r i s 3 . \end{array}$

If a is any non-zero vector, then $(\vec{| a} . \hat{i}) . \hat{i} + (\vec{a} . \hat{j} \cdot) \hat{j} + (\vec{a} . \hat{k}) \hat{k}$ equals _______.

This is a Fill in the blanks type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} L e t \vec{a} = a_{1} \hat{i} + a_{2} \hat{j} + a_{3} \hat{k} \\ ∴ \vec{a} . \hat{i} = (a_{1} \hat{i} + a_{2} \hat{j} + a_{3} \hat{k}) . \hat{i} \\ = a_{1} \\ S i m i l a r l y, \vec{a} . \hat{j} = a_{2} a n d \vec{a} . \hat{k} = a_{3} \\ ∴ (\vec{a} . \hat{i}) . \hat{i} + (\vec{a} . \hat{j}) . \hat{j} + (\vec{a} . \hat{k}) . \hat{k} = a_{1} \hat{i} + a_{2} \hat{j} + a_{3} \hat{k} = \vec{a} \\ H e n c e, t h e v a l u e o f t h e f i l l e r i s \vec{a} . \end{array}$

Vector Algebra True or False Type Question

1. If $\vec{| a}$ | =|

\vec{b} |

, then necessarily it implies $\vec{a}$ = ± $\vec{b}$

Sol:

$\begin{array}{l} I f | \vec{a} | = | \vec{b} | t h e n \vec{a} = \pm \vec{b} w h i c h i s t r u e . \\ H e n c e t h e g i v e n s t a t e m e n t i s T r u e . \end{array}$

2. The position vector of a point P is a vector whose initial point is the origin.

Sol: $T r u e .$

Commonly asked questions

State True or False for the statement in each of the Exercises 41 to 45.

If $\vec{| a}$ | =| $\vec{b} |$ , then necessarily it implies $\vec{a}$ = ± $\vec{b}$

This is a True or False type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} I f | \vec{a} | = | \vec{b} | t h e n \vec{a} = \pm \vec{b} w h i c h i s t r u e . \\ H e n c e t h e g i v e n s t a t e m e n t i s T r u e . \end{array}$

The position vector of a point P is a vector whose initial point is the origin.

This is a True or False type Questions as classified in NCERT Exemplar

Sol: $T r u e .$

If $\vec{| a}$ + $\vec{b} |$ = $\vec{| a}$ - $\vec{b} |$ , then the vectors $\vec{a}$ and $\vec{b}$ are orthogonal.

This is a True or False type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n t h a t | \vec{a} + \vec{b} | = | \vec{a} - \vec{b} | \\ S q u a r i n g b o t h s i d e s, w e g e t \\ {| \vec{a} + \vec{b} |}^{2} = {| \vec{a} - \vec{b} |}^{2} \\ \Rightarrow {| \vec{a} |}^{2} + {| \vec{b} |}^{2} + 2 \vec{a} . \vec{b} = {| \vec{a} |}^{2} + {| \vec{b} |}^{2} - 2 \vec{a} . \vec{b} \\ \Rightarrow 2 \vec{a} . \vec{b} = - 2 \vec{a} . \vec{b} \\ \Rightarrow \vec{a} . \vec{b} = - \vec{a} . \vec{b} \\ \Rightarrow 2 \vec{a} . \vec{b} = 0 \Rightarrow \vec{a} . \vec{b} = 0 \\ w h i c h i m p l i e s t h a t \vec{a} a n d \vec{b} a r e o r t h o g o n a l . \\ H e n c e t h e g i v e n s t a t e m e n t i s T r u e . \end{array}$

The formula ${\vec{(a}}^{} + \vec{b})^{2} + ({\vec{a}}^{2} + {\vec{b}}^{2}) + 2 {(\vec{a} \times \vec{b})}^{2}$ is valid for non-zero vectors $\vec{a}$ and $\vec{b}$ .

This is a True or False type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} {(\vec{a} + \vec{b})}^{2} = (\vec{a} + \vec{b}) . (\vec{a} + \vec{b}) \\ = {| \vec{a} |}^{2} + {| \vec{b} |}^{2} + 2 \vec{a} . \vec{b} \\ H e n c e t h e g i v e n s t a t e m e n t i s F a l s e . \end{array}$

If $\vec{a} \cdot$ and $\vec{b}$ are adjacent sides of a rhombus, then $\vec{a} \cdot \vec{b}$ = 0.

This is a True or False type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} I f \vec{a} . \vec{b} = 0 t h e n \vec{a} . \vec{b} = | \vec{a} | | \vec{b} | c o s 9 0^{0} \\ S o t h e a n g l e b e t w e e n t h e a d j a c e n t s i d e s o f t h e rhombus s h o u l d b e 9 0^{0} w h i c h i s n o t p o s s i b l e . \\ H e n c e t h e g i v e n s t a t e m e n t i s F a l s e . \end{array}$

28th June 2022 (First Shift)

28^th June 2022 (First Shift)

Commonly asked questions

If the system of linear equations

2x + 3y – z = 2

x + y + z = 4

$x - y + | λ | z = 4 λ - 4$ where $λ \in R,$ has no solution, then

System of equation is

$(\begin{matrix} 2 & 3 & - 1 \\ 1 & 1 \\ 1 & - 1 & | λ | \end{matrix}) (\begin{array}{l} x \\ y \\ z \end{array}) = [\begin{array}{l} - 2 \\ 4 \\ 4 λ - 4 \end{array}]$

R₁ – 2 R₂, R₃ – R₂

$(\begin{matrix} 0 & 1 & - 3 \\ 1 & 1 \\ 0 & - 2 & | λ | - 1 \end{matrix}) (\begin{array}{l} x \\ y \\ z \end{array}) = (\begin{array}{l} - 10 \\ 4 \\ 4 λ - 8 \end{array})$

System of equation will have no solution for $λ$ = 7.

Let [t] denote the greatest integer less than or equal to t. Then, the value of the integral $\int_{0}^{1} [- 8 x^{2} + 6 x - 1] d x$ is equal to

$\int_{0}^{1} [- 8 x^{2} + 6 x - 1] d x$

Let f (x) = -8x² + 6x – 1

f (0) = -1, f (1) = -3

max f (x) = $- \frac{D}{4 a} = - \frac{36 - 32}{- 32} = \frac{1}{8}$

= $- \frac{1}{4} - 1 (\frac{3}{4} - \frac{λ}{2}) - 2 (\frac{\sqrt[]{17} - 3}{8} - \frac{3}{4}) - 3 (1 - \frac{\sqrt[]{17} - 3}{8})$

= $\frac{\sqrt[]{17} - 13}{8}$

Let f : R → R be defined as

where a, b, c $\in$ R and [t] denotes greatest integer less than or equal to t. Then, which of the following statements is true?

For x < 0 0 < e^x < 1 Þ [e^x] = 0

$0 \leq x < 1 a e^{x} + [x - 1]$

$= a e^{x} + [x] - 1$

= a e^x – 1 b + [sin px]

$∴ f (x) = [\begin{array}{l} 0 x < 0 \\ a e^{x} - 1 0 \leq x < 1 \\ b - 1 1 \leq x < 2 \\ - c x \geq 2 \end{array}]$

For f to be continuous at x = 0

a – 1 = 0 ⇒ a = 1

$\begin{array}{l} ∴ a + b + c = 1 + e + 1 - e = 2 \\ a + b + c \neq 1 \end{array}$

Let the solution curve y = y(x) of the differential equation $[\frac{x}{\sqrt[]{x^{2} - y^{2}}} + e^{\frac{y}{x}}] x \frac{d y}{d x} = x + [\frac{x}{\sqrt[]{x^{2} - y^{2}}} + e^{\frac{y}{x}}] y$ pass through the points (1, 0) and (2α, α), α > 0. Then a is equal to

$[\frac{x}{\sqrt[]{x^{2} - y^{2}}} + e^{y / x}] x \frac{d y}{d x} = x + [\frac{x}{\sqrt[]{x^{2} - y^{2}}} + e^{y / x}] y$

$\Rightarrow e^{y / x} [x d y - y d x] = x d x + \frac{x}{\sqrt[]{x^{2} - y^{2}}} (y d x - x d y)$

$\Rightarrow e^{y / x} d (y / x) = \frac{d x}{x} - \frac{d (y / x)}{\sqrt[]{1 - {(y / x)}^{2}}}$

Integrating

$e^{y / x} = l n x - s i n^{- 1} (\frac{y}{x}) + c$

Passes (1, 0)

1 = c

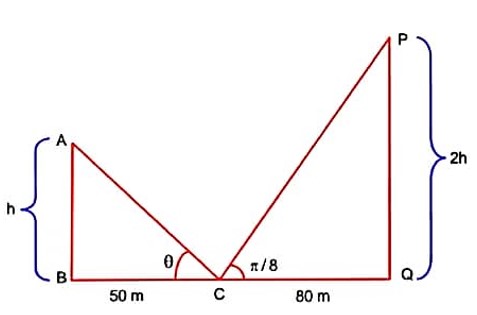
$\Rightarrow α = \frac{1}{2} e x p (\sqrt[]{e} - 1 + \frac{π}{6})$

Let AB and PQ be two vertical poles, 160m apart from each other. Let C be the middle points of B and Q, which are feet of these two poles. Let $\frac{π}{8}$ and q be the angles of elevation from C to P and A, respectively. If the height of pole PQ is twice the height of pole AB, then tan²q is equal to

t a n \frac{π}{8} = \frac{2 h}{80} . . . . . . . . . (i)

$t a n θ = \frac{h}{80} . . . . . . . . . . (i i)$

$\Rightarrow t a n \frac{π}{8} = 2 t a n θ$

$t a n^{2} θ = \frac{3 - 2 \sqrt[]{2}}{4}$

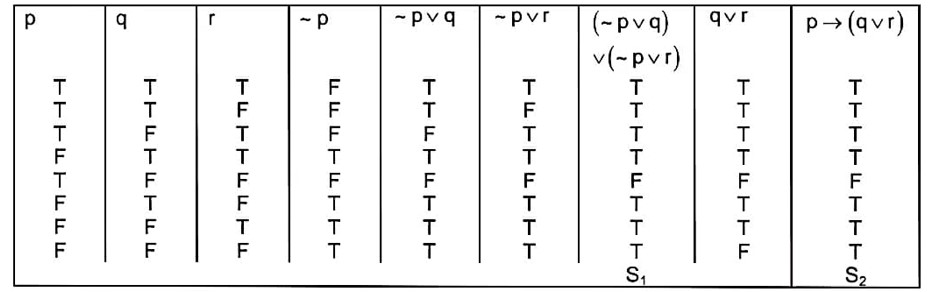
Let p, q, r be three logical statements. Consider the compound statements

$S_{1} : ((\sim p) \lor q) \lor ((\sim p) \lor r) a n d$

$S_{2} : p \to (q \lor r)$

Then, which of the following is NOT true?

Consider the following image

Let R₁ and R₂ be relations on the set {1,2,…., 50} such that

R₁ = ${(p, p^{n}) : p i s a p r i m e a n d n \geq 0 i s a n i n t ? e g e r} a n d$

R₂ = ${(p, p^{n}) : p i s a p r i m e a n d n = 0 o r 1} .$

Then, the number of elements in R₁ – R₂ is…………

A = {1, 2, 3, ….50}

R₁ = (2, 1), (2, 2), (2, 4)…. (2, 32)

(3, 1) (3, 3) (3, 9) (3, 27)

(13, 1) (13, 13) etc.

R₂ = { (2, 1), (2, 2), (3, 1), (3, 3), (5, 1), (5, 5), (7, 1), (7, 7), (1, 1), (11, 11)…}

$∴ R_{1} - R_{2}$ contains only 9 elements.

The mean and standard deviation of 15 observations are found to be 8 and 3 respectively. On rechecking it was found that, in the observations, 20 was misread as 5. Then, the correct variance is equal to…………….

$M e a n \frac{\sum_{i = 1}^{15} x_{i}}{15} = 8$

$\Rightarrow \sum_{i = 1}^{15} x_{i} = 120 . . . . . . . (i)$

S.D = 3

$\Rightarrow \sum_{i = 1}^{15} {x_{i}}^{2} = 15 (9 + 64) = 15 \times 73 . . . . . . . . . . (i i)$

Given 20 has misread as 5

$∴$ in new case

$\sum_{q = 1}^{15} x_{i^{2}} = 15 \times 73 - 25 + 400 = 1470$

mean in new case

$\bar{x} = \frac{120 - 5 + 20}{15}$

$∴ v$ ariance in new case

$σ_{n e w}^{2} = \frac{1}{15} (1470) - 81 = 17$

If $\vec{a} = 2 \hat{i} + \hat{j} + 3 \hat{k}, \vec{b} = 3 \hat{i} + 3 \hat{j} + \hat{k} a n d \vec{c} = c_{1} \hat{i} + c_{2} \hat{j} + c_{3} \hat{k}$ are coplanar vectors and $\vec{a} . \vec{c} = 5, \vec{b} ⊥ \vec{c}, t h e n 122 (c_{1} + c_{2} + c_{3})$ is equal to……….

$\vec{a} = 2 \hat{i} + \hat{j} + 3 \hat{k}$

$\begin{array}{l} \vec{b} = 3 \hat{i} + 3 \hat{j} + \hat{k} \\ \vec{c} = c_{1} \hat{i} + c_{2} \hat{j} + c_{3} \hat{k} \end{array}$

$C o p l n a n a r \Rightarrow | \begin{matrix} 2 & 1 & 3 \\ 3 & 3 & 1 \\ c_{1} & c_{2} & c_{3} \end{matrix} | = 0$

$\begin{array}{l} \Rightarrow - 8 c_{1} + 7 c_{2} + 12 c_{3} = 0 . . . . . . . . (i) \\ \vec{a} . \vec{c} = 5 \Rightarrow 2 c_{1} + c_{2} + 3 c_{3} = 5 . . . . . . . . (i i) \\ \vec{b} . \vec{c} = 0 \Rightarrow 3 c_{1} + 3 c_{2} + c_{3} = 0 . . . . . . . . (i i i) \end{array}$

Solving (i), (ii), (iii)

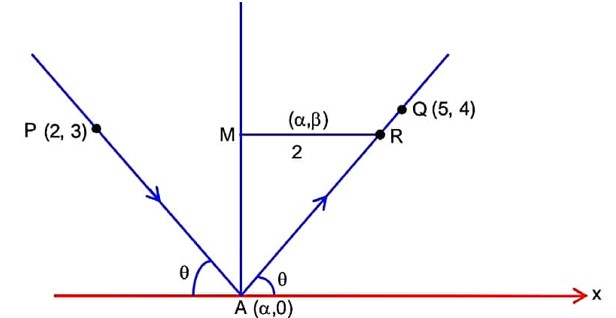
$C_{1} = \frac{10}{122}, c_{2} = \frac{- 85}{122}, c_{3} = \frac{225}{122}$

$∴ 122 (c_{1} + c_{2} + c_{3}) = 150$

A ray of light passing through the point P(2, 3) reflects on the x-axis at point A and the reflected ray passes through the point Q(5, 4). Let R be the point that divides the line segment AQ internally into the ration 2 : 1. Let the co-ordinates of the foot of the perpendicular M from R on the bisector of the angle PAQ be (a, b). Then the value of 7a + 3b is equal to………..

Let $l$ be a line which is normal to the curve y = 2x² + x + 2 at a point P on the curve. If the point Q(6, 4) lies on the line $l$ and O is origin, then the area of the triangle OPQ is equal to

$y = 2 x^{2} + x + 2 . . . . (i)$

$\frac{d y}{d x} = 4 x + 1$

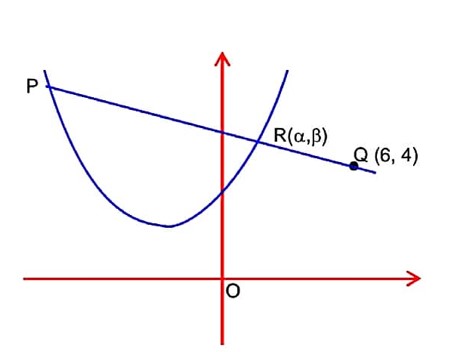
Slope of normal

$- \frac{d x}{d y} = - \frac{1}{4 x + 1}$

Equation of PQ y - β = $- \frac{1}{4 α + 1} (x - α)$

It passes (6, 4)

$\Rightarrow (4 - β) (4 α + 1) = - (6 - α)$

$4 α^{3} + 3 α^{2} - 3 α - 3 = 0$

Let A = ${1, a_{1}, a_{2} . . . . a_{18}, 77}$ be a set of integers with 1 < a₁ < a₂ < … < a₁₈ < 77. Let the set A + A = ${x + y : x, y \in A}$ contains exactly 39 elements. Then, the value of a₁ + a₂ +….. + a₁₈ is equal to

1 < a₁ < a₂ ……18 < 77

77 = 1 + (20 – 1) . d If n numbers are in A.P.

76 = 19 × d ⇒ d = 4

⇒ a₁ = 5

$\begin{array}{l} ∴ a_{1} + a_{2} + . . . . + a_{18} \\ = \frac{18}{2} [2 \times 5 + 17 \times 4] = 702 \end{array}$

The number of elements in the set ${z = a + i b \in C : a, b \in Z a n d 1 < | z - 3 + 2 i | < 4}$ is

$1 < | z - 3 + 2 i | < 4$

$z = a + i b a, b \in I$

⇒ 1 < (a – 3)² + (b + 2)² < 16

in equivalent to 1 < α² + β² < 16 $α = a - 3 \in l$

$(\pm 2, 0) (\pm 3, 0), (0, \pm 2) (0, \pm 3)$ $β = b + 2 \in l$

Total 40 such points are possible

Let the lines y + 2x = $\sqrt[]{11} + 7 \sqrt[]{7}$ and $2 y + x = 2 \sqrt[]{11} + 6 \sqrt[]{7}$ be normal to a circle C : ${(x - h)}^{2} + {(y - k)}^{2} = r^{2} .$ If the line $\sqrt[]{11} y - 3 x = \frac{5 \sqrt[]{77}}{3} + 11$ is tangent to the circle C, then the value of ${(5 h - 8 k)}^{2} + 5 r^{2}$ is equal to

$y + 2 x = \sqrt[]{11} + 7 \sqrt[]{7}$ ……… (i)

$2 y + x = 2 \sqrt[]{11} + 6 \sqrt[]{7}$ ……… (ii)

$\Rightarrow x + y = \sqrt[]{11} + \frac{13}{3} \sqrt[]{7}$ ……… (iii)

Centre of the circle given by solving (i) & (ii)

$a s (\frac{8 \sqrt[]{7}}{3}, \sqrt[]{11} + \frac{5 \sqrt[]{7}}{3})$

Again $\sqrt[]{11} y - 3 x = \frac{5 \sqrt[]{77}}{3}$ is tangent to the circle.

$∴ r = | \frac{\sqrt[]{11} (\sqrt[]{11} + \frac{5 \sqrt[]{7}}{3}) - 8 \sqrt[]{7} - \frac{5 \sqrt[]{77}}{3}}{\sqrt[]{11 + 9}} | = | \frac{11 - 8 \sqrt[]{7}}{\sqrt[]{20}} |$

$∴ {(5 h - 8 k)}^{2} + 5 r^{2} = 816$

If then the value of 16α is equal to

$∴ \frac{α (60!)}{(30!) (31!)} = \frac{62!}{32! 30!} - \frac{60!}{31! 29!}$

$= \frac{(1411) 60!}{(31!) (30!) 16}$

$∴ 16 α = 1411$

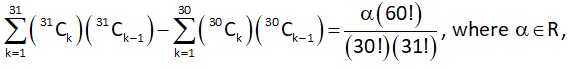
Let a function f : N → N be defined by

$f (n) = [\begin{matrix} 2 n & , & n = 2, 4, 6, 8 . . . . \\ n - 1 & , & n = 3, 7, 11, 15, . . . . \\ \frac{n + 1}{2} & , & n = 1, 5, 9, 13, . . . . . \end{matrix}$

then, f is

$f (x) = [\begin{matrix} 2 n & n = 2, 4, 6 . . . . \\ n - 1 & n = 3, 7, 11, 15 . . . . \\ \frac{n + 1}{2} & n = 1, 5, 9, 13 . . . . \end{matrix}$

for n = 2, 4, 6 ……

f (n) = 4, 8, 12, ….4 (n) form

for n = 3, 7, 11, 15, ….

f (n) = 1, 3, 5, 7, …. (4n + 1) or, (4n + 3) from

$∴$ f is one and onto.

Let A be matrix of order 3 × 3 and det(A) = 2. Then $d e t (d e t (A) a d j (5 a d j (A^{3})))$ is equal to

|A| = 2

$| | A | a d j (5 a d j A^{3}) |$

= $| A P^{3} | | a d j (5 a d j (A^{3})) |$

$\begin{array}{l} = {| A |}^{15} . 5^{6} \\ = 2^{15} \times 5^{6} = 2^{9} \times 1 0^{6} \end{array}$

The total number of 5-digit numbers, formed by using the digits 1, 2, 3, 5, 6, 7 without repetition, which are multiple of 6, is

Sum of digits

1 + 2 + 3 + 5 + 6 + 7 = 24

So, either 3 or 6 rejected at a time

Case 1 Last digit is 2

……….2

no. of cases = ²C₁ × 4! = 48

Case 2 Last digit is 6

……….6

= 4! = 24

Total cases = 72

Let A₁, A₂, A₃,…. be an increasing geometric progression of positive real numbers. If A₁A₃A₅A₇ = $\frac{1}{1296}$ and A₂ + A₄ = $\frac{7}{36},$ then, the value of A₆ + A₈ + A₁₀ is equal to

Let $\frac{A_{2}}{A_{1}} = \frac{A_{3}}{A_{2}} = . . . = r$

$∴ A_{1} A_{3} A_{5} A_{7} = \frac{1}{1296}$

$\Rightarrow A_{1} r^{3} = \frac{1}{6} . . . . . . . (i)$

Again, A₂ + A₄ = $\frac{7}{36}$

$A_{1} r = \frac{7}{36} - \frac{1}{6} = \frac{1}{36} . . . . . . . . (i i)$

$(i) & (i i) r = \sqrt[]{6} & A_{1} = \frac{1}{36 \sqrt[]{6}}$

$∴ A_{6} + A_{8} + A_{10} = A_{1} r^{5} (1 + r^{2} + r^{4}) = 43$

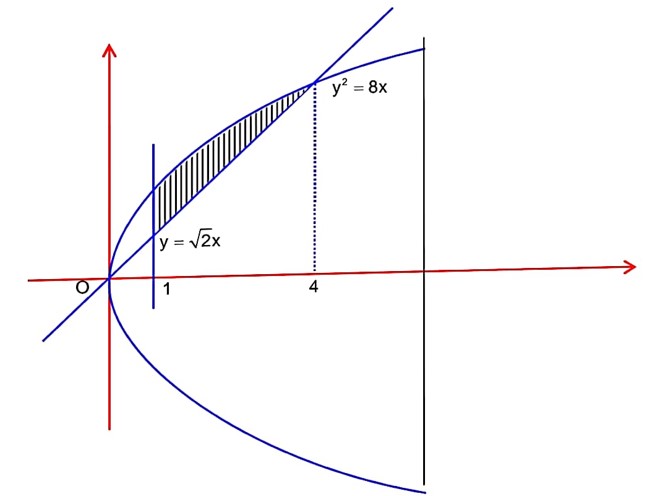
The area of the region S = ${(x, y) : y^{2} \leq 8 x, y \geq \sqrt[]{2} x, x \geq 1}$ is

Let y = y(x) be the solution of the differential equation $x (1 - x^{2}) \frac{d y}{d x} + (3 x^{2} y - y - 4 x^{3}) = 0, x > 1, w i t h y (2) = - 2 .$ Then y(3) is equal to

$x (1 - x^{2}) \frac{d y}{d x} + (3 x^{2} y - y - 4 x^{3}) = 0$

$\Rightarrow x (1 - x^{2}) \frac{d y}{d x} + (3 x^{2} - 1) y = 4 x^{3}$

$\Rightarrow y = 2 x - 1 (x^{3} - x) ∴ y (3) = - 18$

Let the eccentricity of the hyperbola $H : \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 b e \sqrt[]{\frac{5}{2}}$ and length of its latus rectum be $6 \sqrt[]{2}, i f y = 2 x + c$ is a tangent to the hyperbola H, then the value of c²is equal to

$a^{2} (e^{2} - 1) = b^{2}$

$e = \sqrt[]{\frac{5}{2}} \Rightarrow b^{2} = \frac{3 a^{2}}{2}$

Length of latus rectum $\frac{2 b^{2}}{a} = 6 \sqrt[]{2}$

$3 a = 6 \sqrt[]{2} \Rightarrow a = 2 \sqrt[]{2}$

$b = 2 \sqrt[]{3}$

y = 2x + c is tangent to hyperbola

$∴ c^{2} = a^{2} m^{2} - b^{2} = 20$

If the tangents drawn at the points O(0, 0) and $P (1 + \sqrt[]{5}, 2)$ on the circle x² + y² – 2x – 4y = 0 intersect at the point Q, then the area of the triangle OPQ is equal to

x^{2} + y^{2} - 2 x - 4 y = 0

Centre (1, 2) r = $\sqrt[]{5}$

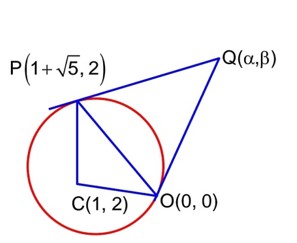
Equation of OQ is x . 0 + y . 0 – (x + 0) – 2 (y + 0) = 0

⇒ x + 2y = 0 ……… (i)

Equation of PQ is $x (1 + \sqrt[]{5}) + 2 y - (| x + 1 + \sqrt[]{5}) - 2 (y + 2) = 0$

Solving (i) & (ii), $Q (\sqrt[]{5} + 1, - \frac{\sqrt[]{5} + 1}{2})$

$= \frac{1}{2} | \frac{6 + 2 \sqrt[]{5} + 4 \sqrt[]{5} = 4}{2} | = \frac{6 \sqrt[]{5} + 10}{4} = \frac{3 \sqrt[]{5} + 5}{2}$

If two distinct points Q, R lie on the line of intersection of the planes x + 2y – z = 0 and 3x 5y + 2z = 0 and PQ = PR = $\sqrt[]{18}$ where the point P is (1, 2, 3), then the area of the triangle PQR is equal to

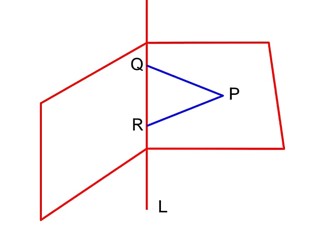
Let vector along L is $\vec{x}$

$\vec{x} = | \begin{matrix} i & j & k \\ - 1 & 2 & - 1 \\ 3 & - 5 & 2 \end{matrix} |$

= $- \hat{i} - \hat{j} - \hat{k}$

Area of $Δ P Q R = \frac{1}{2} | \vec{P Q} \times \vec{P R} |$

$= \frac{1}{2} | \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & 4 & - 1 \\ \frac{- 5}{3} & \frac{4}{3} & - \frac{11}{3} \end{matrix} |$

$= \frac{4}{3} \sqrt[]{38}$

The acute angle between the planes P₁ and P₂, when P₁ and P₂ are the planes passing through the intersection of the planes 5x + 8y + 13z – 29 = 0 and 8x – 7y + z – 20 = 0 and the points (2, 1, 3) and (0, 1, 2), respectively, is

$(5 x + 8 y + 13 z - 29) + λ (8 x - 7 y + z - 20) = 0$

P₁ passing (2, 1, 3)

(10 + 8 + 39 – 29) + $λ (16 - 7 + 3 - 20) = 0$

$28 - 8 λ = 0 λ = 7 / 2$

$\Rightarrow$ 2X – Y + Z – 6 = 0 …..(i)

For P₂ passes (0, 1, 2)

$(8 + 26 - 29) + λ (- 7 + 2 - 20) = 0$

$5 - 25 λ = 0 \Rightarrow λ = \frac{1}{5}$

$P_{2} : x + y + 2 z - 5 = 0 . . . . . . . . (i i)$

Acute angle between the planes

$c o s θ = \frac{2 - 1 + 2}{\sqrt[]{4 + 1 + 1} \sqrt[]{1 + 1 + 4}} = \frac{1}{2}$

$\Rightarrow θ = \frac{π}{3}$

Let the plane $P : \vec{r} . \vec{a} = d$ contains the line of intersection of two planes $\vec{r} . (\hat{i} + 3 \hat{j} - \hat{k}) = 6$ and $\vec{r} . (6 \hat{i} + 5 \hat{j} - \hat{k}) = 7 .$ If the plane P passes through the point $(2, 3, \frac{1}{2})$ , then the value of $\frac{{| 13 \vec{a} |}^{2}}{d^{2}}$ is equal to

$P : (x + 3 y - z - 6) = λ (- 6 x + 5 y - z - 7) = 0$

Passes $(2, 3, \frac{1}{2})$

$\Rightarrow (2 + 9 - \frac{1}{2} - 6) = λ (- 12 + 15 - \frac{1}{2} - 7) = 0$

$\Rightarrow λ = 1$

$\frac{{| 13 \vec{a} |}^{2}}{d^{2}} = \frac{{(13)}^{2} (93)}{{(13)}^{2}} = 93$

The probability, that in a randomly selected 3-digit number at least two digits are odd, is

aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa

The number of real solutions of the equation e^4x + 4e^3x – 58e^2x + 4e^x + 1 = 0, is……………

$e^{4 x} + 4 e^{3 x} - 58 e^{2 x} + 4 e^{x} + 1 = 0$

$(e^{2 x} + \frac{1}{e^{2 x}}) + 4 (e^{x} + \frac{1}{e^{x}}) - 58 = 0$

$\Rightarrow {(e^{x} + \frac{1}{e^{x}} + 2)}^{2} = 64$

$e^{x}$ $=$ $\frac{6 \pm 32}{2}$ $=$ $3$ $\pm$ $2$

The number of positive integers k such that the constant term in the binomial expansion of ${(2 x^{3} + \frac{3}{x^{k}})}^{12}, x \neq 0 i s 2^{8} . l, w h e r e l$ is an odd integer, is………..

${(2 x^{3} + \frac{3}{x^{k}})}^{12}$

gen term =

$=^{12} C_{r} 2^{12 - r} . 3^{r} . x^{36 - 3 r - r k}$

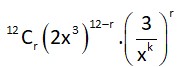
For constant term

36 – 3r – rk = 0

$\Rightarrow k = \frac{36 - 3 r}{r}$

for r = 1, 2, 4

¹²C_r2^12-r>2⁸

Possible values of k = 3, 1

JEE Mains 2022

Commonly asked questions

The sum, of all real values of x for which $\frac{3 x^{2} - 9 x + 17}{x^{2} + 3 x + 10} = \frac{5 x^{2} - 7 x + 19}{3 x^{2} + 5 x + 12}$ is equal to…………….

$\frac{3 x^{2} - 9 x + 17}{x^{2} + 3 x + 10} = \frac{5 x^{2} - 7 x + 19}{3 x^{2} + 5 x + 12}$

$1 + \frac{2 x^{2} - 12 x + 7}{x^{2} + 3 x + 10} = 1 + \frac{2 x^{2} - 12 x + 7}{3 x^{2} + 5 x + 12}$

$(2 x^{2} - 12 x + 7) (\frac{1}{x^{2} + 3 x + 10} - \frac{1}{3 x^{2} + 5 x + 12}) = 0$

Let S be the set of all passwords which are six to eight characters long, where each character is either an alphabet form ${A, B, C, D, E}$ or a number from ${1, 2, 3, 4, 5}$ with the repetition of characters allowed. If the number of passwords in S whose at least one character is a number from ${1, 2, 3, 4, 5} i s α \times 5^{6},$ $^{}$ then is equal to………….

Required number = Total – no character from {1, 2, 3, 4, 5}

$= (1 0^{6} - 5^{6}) + (1 0^{7} - 5^{7}) + (1 0^{8} - 5^{8})$

$= 5^{6} (2^{6} \times 111 - 31) = 5^{6} \times \frac{7073}{α}$

= 7073

Let $P (- 2, - 1, 1)$ and $Q (\frac{56}{17}, \frac{43}{17}, \frac{111}{17})$ be the vertices of the rhombus PQRS. If the direction ratios of the diagonal RS are a, -1, b where both a and b are integers of minimum absolute values, then α² + β² is equal to………..

$R S \equiv (α, -, 1 β)$

$D R o f P Q \equiv (\frac{56}{17} + 2, \frac{43}{17} + 1, \frac{111}{17} - 1)$

$\equiv (\frac{90}{17}, \frac{60}{17}, \frac{94}{17})$

$90 α + 94 β = 60$

$\begin{array}{l} β = - 15, α = - 15 \\ α^{2} + β^{2} = 450 \end{array}$

Let f: [0, 1] R be a twice differentiable function in (0, 1) such that f(0) = 3 and f(1) = 5. If the line y =2x + 3 intersects the graph of f at only two distinct points in (0, 1), then the least number of points $x \in (0, 1),$ at which $f " (x) = 0,$ is…………….

$f' (a) = f' (b) = f' (c) = 2$

f’’ (x) is zero for atleast $x_{1} \in (a, b) & x_{2} \in (b, c)$ $_{}_{}$

If $\int_{0}^{\sqrt[]{3}} \frac{15 x^{3}}{\sqrt[]{1 + x^{2} + \sqrt[]{{(1 + x^{2})}^{3}}}} d x = α \sqrt[]{2} + β \sqrt[]{3},$ where a, b are integers, then α + β is equal to………..

Put $1 + x^{2} = t^{2} \Rightarrow 2 x d x = 2 t d t$

$∴ \int_{1}^{2} \frac{15 (t^{2} - 1) t d t}{\sqrt[]{t^{2} + t^{3}}} d t$ Put (1 + t) = u²

$30 \int_{\sqrt[]{2}}^{\sqrt[]{3}} (u^{4} - 2 u^{2}) d u$ dt = 2u du

$= - 6 \sqrt[]{3} + 16 \sqrt[]{2} = α \sqrt[]{2} + β \sqrt[]{3}$

$\begin{array}{l} α = 16, β = - 6 \\ ∴ α + β = 10 \end{array}$

Let $A = [\begin{matrix} 1 & - 1 \\ 2 & α \end{matrix}] a n d B = [\begin{matrix} β & 1 \\ 1 & 0 \end{matrix}], α, β \in R .$ Let a₁ be the value of a which satisfies $(A + B) = A^{2} + [\begin{matrix} 2 & 2 \\ 2 & 2 \end{matrix}] a n d α_{2}$ be the value of a which satisfies (A + B)² = B². Then $| α_{1} - α_{2} |$ is equal to…………….

$A + B = [\begin{matrix} β + 1 & 0 \\ 3 & α \end{matrix}]$

${(A + B)}^{2} = [\begin{matrix} {(β + 1)}^{2} & 0 \\ 3 (β + 1) + 3 α & α^{2} \end{matrix}]$

$∴ [\begin{matrix} 1 & - α + 1 \\ 2 α + 4 & α^{2} \end{matrix}] = [\begin{matrix} {(β + 1)}^{2} & 0 \\ 3 (α + β + 1) & α^{2} \end{matrix}]$

= 1 = 1

$B^{2} = [\begin{matrix} β & 1 \\ 1 & 0 \end{matrix}] [\begin{matrix} β & 1 \\ 1 & 0 \end{matrix}]$

$β = 0, α = - 1 = α_{2}$

$| α_{1} - α_{2} | = | 1 - (- 1) | = 2$

For p, q $\in R,$ consider the real valued function f(x) = (x – p)² – q, $x \in R$ and q > 0. Let a₁, a₂, a₃ and a₄ be in an arithmetic progression with mean p and positive common difference. If $| f (a_{i}) | = 500$ for all I = 1, 2, 3, 4, then the absolute difference between the roots of f(x) = 0 is………….

$f (x) = 0 \Rightarrow {(x - p)}^{2} - q = 0$

Roots are $p + \sqrt[]{q}, p - \sqrt[]{q}$

Now, $| f (a_{i}) | = 500$

$L e t a_{1}, a_{2}, a_{3} . . . a r a, a + d, a + 2 d, a + 3 d$

=> $\frac{9}{4} d^{2} - q = 500$ …….(i)

and ${| f (a_{1}) |}^{2} = {| f (a_{2}) |}^{2}$

From equation (i)

$\frac{9}{4} . \frac{4 q}{5} - q = 500$

$\frac{4 q}{5} = 500$

and $2 \sqrt[]{q} = 2 \times \frac{50}{2} = 50$

For the hyperbola H: x² – y² = 1 and the ellipse E : $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1,$ a > b > 0, let the

(1) eccentricity of E be reciprocal of the eccentricity of H, and

(2) the line y = $\sqrt[]{\frac{5}{2}} x + K$ be a common tangent of E and H.

Then 4(a² + b²) is equal to……………..

$e_{E} = \sqrt[]{1 - \frac{b^{2}}{a^{2}}}, e_{H} = \sqrt[]{2}$

$I f \Rightarrow e_{E} = \frac{1}{e_{H}} \Rightarrow \frac{a^{2} - b^{2}}{a^{2}} = \frac{1}{2}$

$k^{2} = a^{2} \times \frac{5}{2} + b^{2} = \frac{3}{2}$

$6 b^{2} = \frac{3}{2} \Rightarrow b^{2} = \frac{1}{4} a n d a^{2} = \frac{1}{2}$

$∴ 4 (a^{2} + b^{2}) = 3$

Let x₁, x₂, x₃,……..x₂₀ be in geometric progression with x₁ = 3 and the common ratio $\frac{1}{2} .$ A new data is constructed replacing each x_i by (x_i – i)². If $\bar{x}$ is the mean of new data, then the greatest integer less than or equal to $\bar{x}$ is………….

$\sum_{}^{} x_{0}^{1} = \frac{3 {(1 - (\frac{1}{2}))}^{20}}{1 - \frac{1}{2}} = 6 (1 - \frac{1}{2^{20}})$

$= \sum_{i = 1}^{20} {(x_{i})}^{2} + {(i)}^{2} - 2 x_{i} i$

Now, $\sum_{i = 1}^{20} {(x_{i})}^{2} = \frac{9 {(1 - (\frac{1}{4}))}^{20}}{(1 - \frac{1}{4})} = 12 (1 - \frac{1}{2^{40}})$

$\bar{x} = \frac{2858}{20} + (\frac{- 12}{2^{40}} + \frac{22}{2^{20}}) \times \frac{1}{20}$

$[\bar{x}] = 142$

$\underset{x \to 0}{l i m} {(\frac{{(x + 2 c o s x)}^{3} + 2 {(x + 2 c o s x)}^{2} + 3 s i n x (x + 2 c o s x)}{{(x + 2)}^{3} + 2 {(x + 2)}^{2} + 3 s i n (x + 2)})}^{\frac{100}{x}}$ is equal to………….

$\underset{x \to 10}{l i m} {(\frac{{(x + 2 c o s x)}^{3} + 2 {(x + 2 c o s x)}^{2} + 3 s i n (x + 2 c o s x)}{{(x + 2)}^{3} \pm 2 {(x + 2)}^{2} + 3 s i n (x + 2)})}^{x}$

$e^{\frac{100}{16 + 3 s i n 2} [\frac{12 - 3 (4) + 8 \times 1 - 8 + 3 c o s 2 - 3 c o s 2}{1}]}$ , using L.H.L Rule, e0 = 1

$2 x^{2} - 12 x + 7 = 0 o r 3 x^{2} + 5 x + 12 = x^{2} + 3 x + 10$

$x^{2} + x + 1 = 0$

Sum of roots = 6, no solution.

Commonly asked questions

The sum, of all real values of x for which $\frac{3 x^{2} - 9 x + 17}{x^{2} + 3 x + 10} = \frac{5 x^{2} - 7 x + 19}{3 x^{2} + 5 x + 12}$ is equal to…………….

$\frac{3 x^{2} - 9 x + 17}{x^{2} + 3 x + 10} = \frac{5 x^{2} - 7 x + 19}{3 x^{2} + 5 x + 12}$

$1 + \frac{2 x^{2} - 12 x + 7}{x^{2} + 3 x + 10} = 1 + \frac{2 x^{2} - 12 x + 7}{3 x^{2} + 5 x + 12}$

$(2 x^{2} - 12 x + 7) (\frac{1}{x^{2} + 3 x + 10} - \frac{1}{3 x^{2} + 5 x + 12}) = 0$

Required number = Total – no character from {1, 2, 3, 4, 5}

$= (1 0^{6} - 5^{6}) + (1 0^{7} - 5^{7}) + (1 0^{8} - 5^{8})$

$= 5^{6} (2^{6} \times 111 - 31) = 5^{6} \times \frac{7073}{α}$

= 7073

$R S \equiv (α, -, 1 β)$

$D R o f P Q \equiv (\frac{56}{17} + 2, \frac{43}{17} + 1, \frac{111}{17} - 1)$

$\equiv (\frac{90}{17}, \frac{60}{17}, \frac{94}{17})$

$90 α + 94 β = 60$

$\begin{array}{l} β = - 15, α = - 15 \\ α^{2} + β^{2} = 450 \end{array}$

$f' (a) = f' (b) = f' (c) = 2$

f’’ (x) is zero for atleast $x_{1} \in (a, b) & x_{2} \in (b, c)$ $_{}_{}$

If $\int_{0}^{\sqrt[]{3}} \frac{15 x^{3}}{\sqrt[]{1 + x^{2} + \sqrt[]{{(1 + x^{2})}^{3}}}} d x = α \sqrt[]{2} + β \sqrt[]{3},$ where a, b are integers, then α + β is equal to………..

Put $1 + x^{2} = t^{2} \Rightarrow 2 x d x = 2 t d t$

$∴ \int_{1}^{2} \frac{15 (t^{2} - 1) t d t}{\sqrt[]{t^{2} + t^{3}}} d t$ Put (1 + t) = u²

$30 \int_{\sqrt[]{2}}^{\sqrt[]{3}} (u^{4} - 2 u^{2}) d u$ dt = 2u du

$= - 6 \sqrt[]{3} + 16 \sqrt[]{2} = α \sqrt[]{2} + β \sqrt[]{3}$

$\begin{array}{l} α = 16, β = - 6 \\ ∴ α + β = 10 \end{array}$

$A + B = [\begin{matrix} β + 1 & 0 \\ 3 & α \end{matrix}]$

${(A + B)}^{2} = [\begin{matrix} {(β + 1)}^{2} & 0 \\ 3 (β + 1) + 3 α & α^{2} \end{matrix}]$

$∴ [\begin{matrix} 1 & - α + 1 \\ 2 α + 4 & α^{2} \end{matrix}] = [\begin{matrix} {(β + 1)}^{2} & 0 \\ 3 (α + β + 1) & α^{2} \end{matrix}]$

= 1 = 1

$B^{2} = [\begin{matrix} β & 1 \\ 1 & 0 \end{matrix}] [\begin{matrix} β & 1 \\ 1 & 0 \end{matrix}]$

$β = 0, α = - 1 = α_{2}$

$| α_{1} - α_{2} | = | 1 - (- 1) | = 2$

$f (x) = 0 \Rightarrow {(x - p)}^{2} - q = 0$

Roots are $p + \sqrt[]{q}, p - \sqrt[]{q}$

Now, $| f (a_{i}) | = 500$

$L e t a_{1}, a_{2}, a_{3} . . . a r a, a + d, a + 2 d, a + 3 d$

=> $\frac{9}{4} d^{2} - q = 500$ …….(i)

and ${| f (a_{1}) |}^{2} = {| f (a_{2}) |}^{2}$

From equation (i)

$\frac{9}{4} . \frac{4 q}{5} - q = 500$

$\frac{4 q}{5} = 500$

and $2 \sqrt[]{q} = 2 \times \frac{50}{2} = 50$

For the hyperbola H: x² – y² = 1 and the ellipse E : $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1,$ a > b > 0, let the

(1) eccentricity of E be reciprocal of the eccentricity of H, and

(2) the line y = $\sqrt[]{\frac{5}{2}} x + K$ be a common tangent of E and H.

Then 4(a² + b²) is equal to……………..

$e_{E} = \sqrt[]{1 - \frac{b^{2}}{a^{2}}}, e_{H} = \sqrt[]{2}$

$I f \Rightarrow e_{E} = \frac{1}{e_{H}} \Rightarrow \frac{a^{2} - b^{2}}{a^{2}} = \frac{1}{2}$

$k^{2} = a^{2} \times \frac{5}{2} + b^{2} = \frac{3}{2}$

$6 b^{2} = \frac{3}{2} \Rightarrow b^{2} = \frac{1}{4} a n d a^{2} = \frac{1}{2}$

$∴ 4 (a^{2} + b^{2}) = 3$

$\sum_{}^{} x_{0}^{1} = \frac{3 {(1 - (\frac{1}{2}))}^{20}}{1 - \frac{1}{2}} = 6 (1 - \frac{1}{2^{20}})$

$= \sum_{i = 1}^{20} {(x_{i})}^{2} + {(i)}^{2} - 2 x_{i} i$

Now, $\sum_{i = 1}^{20} {(x_{i})}^{2} = \frac{9 {(1 - (\frac{1}{4}))}^{20}}{(1 - \frac{1}{4})} = 12 (1 - \frac{1}{2^{40}})$

$\bar{x} = \frac{2858}{20} + (\frac{- 12}{2^{40}} + \frac{22}{2^{20}}) \times \frac{1}{20}$

$[\bar{x}] = 142$

$\underset{x \to 10}{l i m} {(\frac{{(x + 2 c o s x)}^{3} + 2 {(x + 2 c o s x)}^{2} + 3 s i n (x + 2 c o s x)}{{(x + 2)}^{3} \pm 2 {(x + 2)}^{2} + 3 s i n (x + 2)})}^{x}$

$e^{\frac{100}{16 + 3 s i n 2} [\frac{12 - 3 (4) + 8 \times 1 - 8 + 3 c o s 2 - 3 c o s 2}{1}]}$ , using L.H.L Rule, e0 = 1

$2 x^{2} - 12 x + 7 = 0 o r 3 x^{2} + 5 x + 12 = x^{2} + 3 x + 10$

$x^{2} + x + 1 = 0$

Sum of roots = 6, no solution.

Maths NCERT Exemplar Solutions Class 12th Chapter Ten Exam

Student Forum

Anything you would want to ask experts?

Write here...

Other Similar chapters for you

Vector Algebra

News & Updates

Latest NewsPopular News

Maths NCERT Exemplar Solutions Class 12th Chapter Ten: Overview, Questions, Preparation

Vector Algebra Short Answer Type Questions

Commonly asked questions

Vector Algebra Long Answer Type Questions

Commonly asked questions

Vector Algebra Objective Type Questions

Commonly asked questions

Vector Algebra Fill in the blanks

Commonly asked questions

Vector Algebra True or False Type Question

Commonly asked questions

28th June 2022 (First Shift)

Commonly asked questions

JEE Mains 2022

Commonly asked questions

Commonly asked questions

Student Forum

Other Similar chapters for you

News & Updates

NMAT Registration 2025 Last date (Oct 18) @mba.com; Live Updates

UPPSC PCS 2025 Prelims Answer Key Download Link (Official PDF) @uppsc.up.nic.in Live Updates

NEET PG Rank wise Seat Allotment 2025: Check Branch-wise Expected Closing Ranks

Gujarat Board Exam Dates 2026 Class 10th, 12th Soon @gseb.org; Live Updates on GSEB SSC, HSC Time Table

JEE Main Marks vs Percentile vs Rank 2025: Calculate Percentile and Rank Using Marks

List of NIT Colleges in India 2025 - NIRF Ranking, Courses, Seats, Cutoff, Fees and Placement

CBSE 10th Maths Question Paper 2025, 2024, 2023, 2022, 2020, 2019 PDF Download

NEET Chapter Wise Weightage 2026 PDF by NTA: Physics, Chemistry & Biology

List of Top IITs in India 2025: NIRF Ranking, Courses, Seats, Fees & Placement