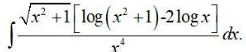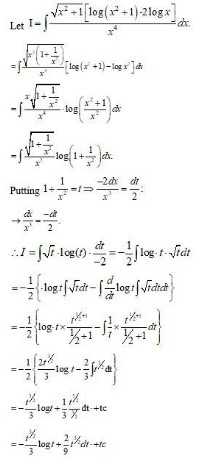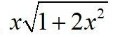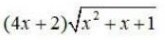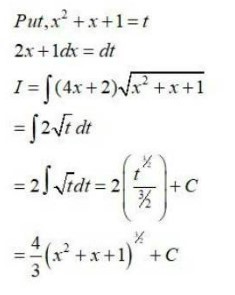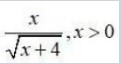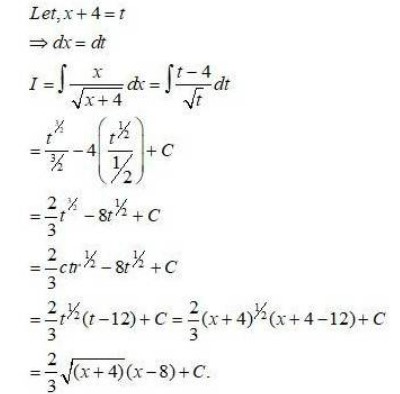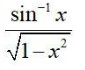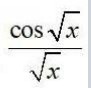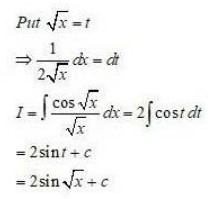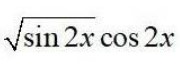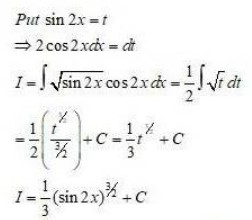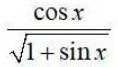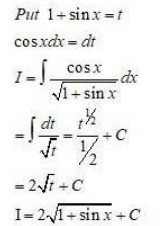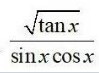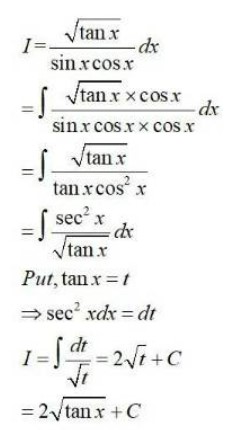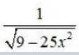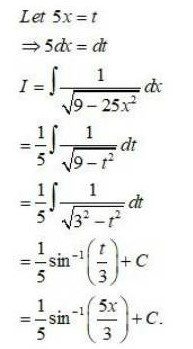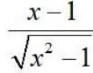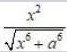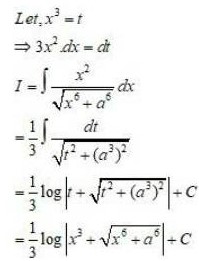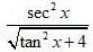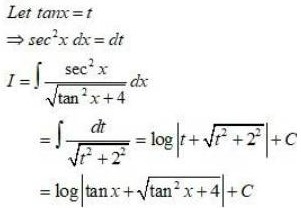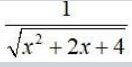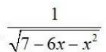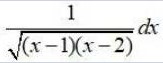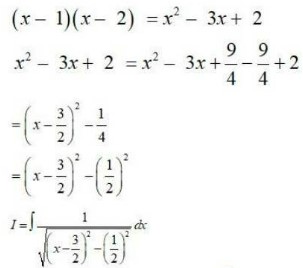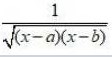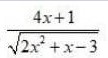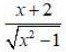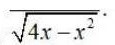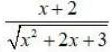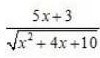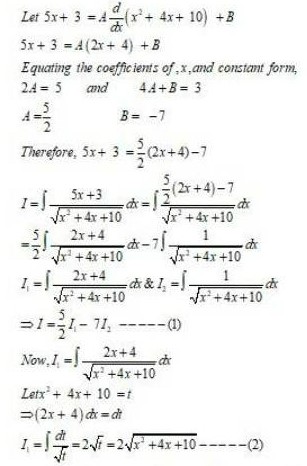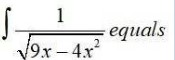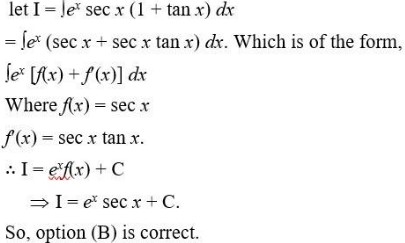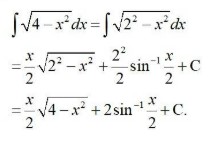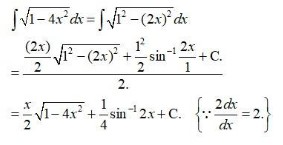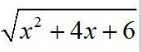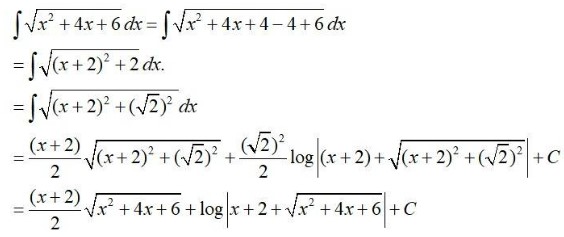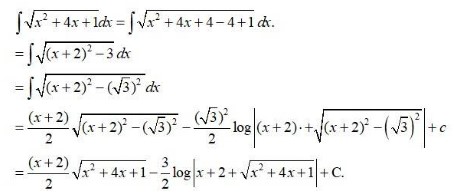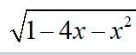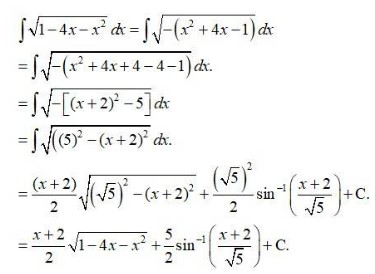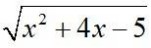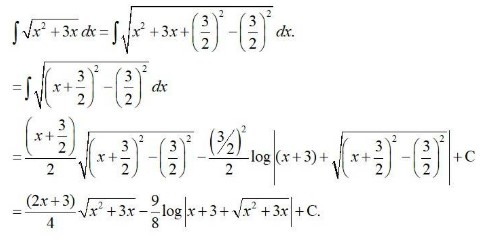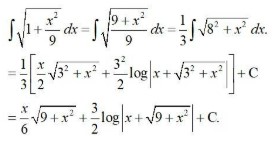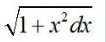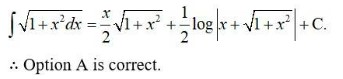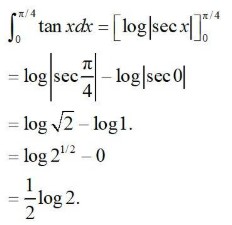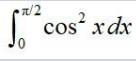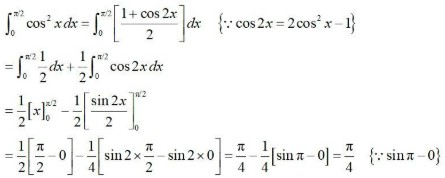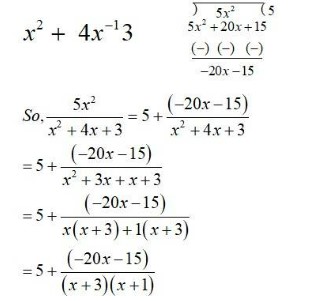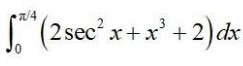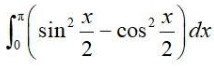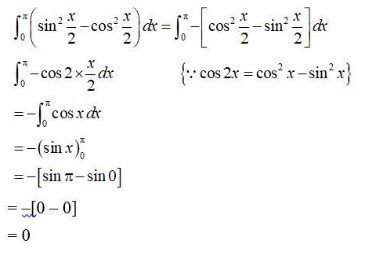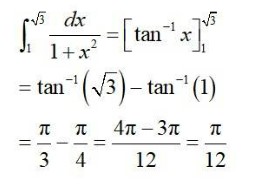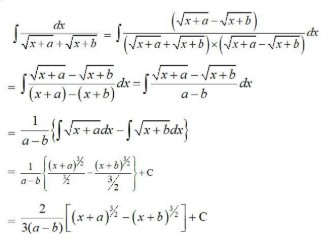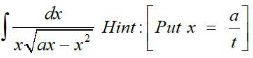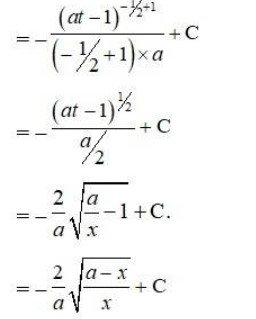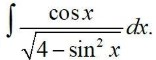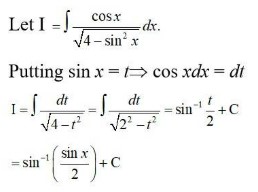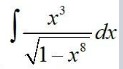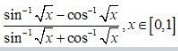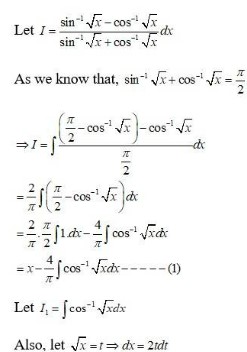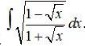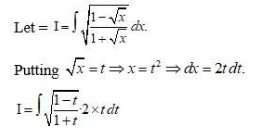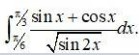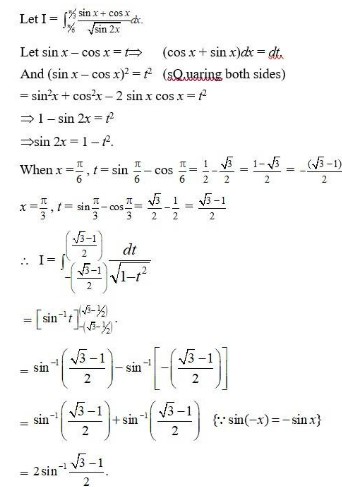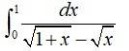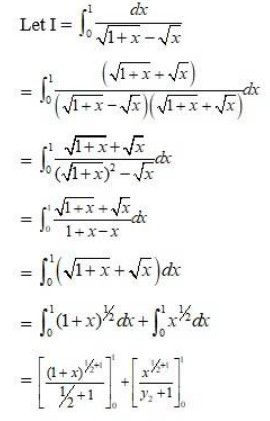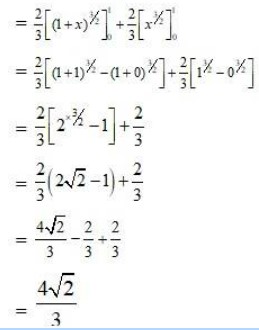Integrals Class 12 NCERT Solutions cover two types of integrals - definite and indefinite integrals, which are together called the Integral Calculus. Between the indefinite and definite integrals, there is a connection called the Fundamental Theorem of Calculus. This connection makes the definite integral a practical tool for engineering and science.
Class 12 Integrals concepts are important as it has applications in various industries. The definite integral is used to solve many interesting problems from various fields like probability, finance, and economics. The chapter also includes the elementary properties of the definite and indefinite integrals, including some techniques of integration.
If you are looking for Class 12 Maths notes for CBSE Board exam preparation, check - Class 12 Maths Notes. You will get the solved examples with chapter-wise PDFs.
- Insight into Class 12 Maths Chapter 7 Integrals NCERT Solutions
- Class 12 Math Chapter 7 Integral: Key Topics, Weightage
- Important Formulas of Class 12 Integrals
- Topics Covered in NCERT Maths Class 12 Integrals Chapter
- NCERT Maths Class 12th Solution PDF - Integrals Chapter Download
- Integrals Questions and Answers
Insight into Class 12 Maths Chapter 7 Integrals NCERT Solutions
Here is a quick review of the Integrals Class 12:
- The chapter is about integration, which is the inverse process of differentiation. Here, the differential of a function is given, and we need to find the function.
- Some properties of indefinite integrals are -
- The chapter also includes the standard integrals, integration by partial function, integration by substitution, and integrals of some special functions.
- Other concepts covered in this chapter include integration by parts, some special types of integrals, and the first fundamental theorem of integral calculus.
Related Links
| NCERT Notes for Class 11 & 12 | Class 12 Maths NCERT Solutions | NCERT Solutions Class 11 and 12 |
Class 12 Math Chapter 7 Integral: Key Topics, Weightage
Class 12 Integrals is an important chapter for entrance tests. Students should clearly understand the concepts of the chapter to score well in the CBSE Board exam and competitive exams like JEE Mains. Here are the topics covered in this chapter:
| Exercise | Topics Covered |
|---|---|
| 7.1 | Introduction |
| 7.2 | Integration as an Inverse Process of Differentiation |
| 7.3 | Methods of Integration |
| 7.4 | Integrals of Some Particular Functions |
| 7.5 | Integration by Partial Fractions |
| 7.6 | Integration by Parts |
| 7.7 | Definite Integral |
| 7.8 | Fundamental Theorem of Calculus |
| 7.9 | Evaluation of Definite Integrals by Substitution |
| 7.10 | Some Properties of Definite Integrals |
Class 12 Integrals Weightage in JEE Main
| Exam | Number of Questions | Total Marks | Weightage |
|---|---|---|---|
| JEE Main | 3 questions | Generally worth around 12 marks | 9-10% |
Those who are looking for comprehensive NCERT notes of Physics, Chemistry & Maths of class 12, must explore at - NCERT Class 12 Notes.
Important Formulas of Class 12 Integrals
Important Formulae for Class 12 Math Integrals
Topics Covered in NCERT Maths Class 12 Integrals Chapter
- Integration as an Inverse Process of Differentiation
- Methods of Integration
- Integrals of Some Particular Functions
- Integration by Partial Fractions
- Integration by Parts
- Definite Integral
- Fundamental Theorem of Calculus
- Evaluation of Definite Integrals by Substitution
- Some Properties of Definite Integrals
NCERT Maths Class 12th Solution PDF - Integrals Chapter Download
Integrals Class 12 NCERT Solutions PDF download link is given here. Students should download it to get the well-structured solutions to all the exercises of this chapter. It offers reliable and accurate study material for exam preparation.
Download Here: NCERT Solution for Class XII Maths Integrals PDF
Integrals Questions and Answers
| Find an anti-derivative (or integral) of the following functions by the method of inspection. Q1. |
| A.1.
Therefore, an anti-derivative of |
| Q2. |
| A.2.
Therefore, an anti-derivative of |
| Q3. |
| A.3.
Therefore, an anti-derivative of |
| Q4. |
| A.4.
Therefore, an anti-derivative of |
Commonly asked questions
Kindly Consider the following
103.
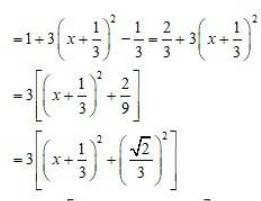

Kindly Consider the following
73.
Kindly Consider the following
79.
Kindly Consider the following
Kindly Consider the following
24.
Kindly Consider the following
27.
Kindly Consider the following
32.
Kindly Consider the following
77.
I
Kindly Consider the following
81.
Kindly Consider the following
82.
Kindly Consider the following
83.
Kindly Consider the following
85.
87. Kindly Consider the following
Kindly go through the solution
88. Kindly Consider the following
Kindly go through the solution
Kindly Consider the following
144. 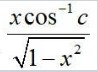
Kindly go through the solution
Kindly Consider the following
145.
251. Kindly Consider the following
Kindly go through the solution

Kindly Consider the following
70.
ind an anti-derivative (or integral) of the following functions by the method of inspection.
1.
Therefore, an anti-derivative of
Kindly Consider the following
28. √ax + b
Kindly Consider the following
29.
Kindly Consider the following
36.
Kindly Consider the following
71.
Kindly Consider the following
72.
Kindly go through the solution

Kindly Consider the following
74.
Kindly Consider the following
75.
Kindly Consider the following
76.
Find the following integrals in Exercises 6 to 20:
6.
=
Kindly Consider the following
41.
Dividing both numerator and denominator by ex, we get
Kindly Consider the following
42.
Kindly Consider the following
60.
Therefore, the correct answer is (D)
Kindly Consider the following
61.
Therefore, the correct answer is B.
Kindly Consider the following
2.
Therefore, an anti-derivative of
Kindly Consider the following
3.
Therefore, an anti-derivative of
Kindly Consider the following
4.
Therefore, an anti-derivative of
Kindly Consider the following
5.
Therefore, an anti-derivative of
Kindly Consider the following
7.
Kindly Consider the following
8.
Kindly Consider the following
9.
Kindly Consider the following
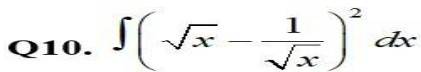
Kindly go through the solution

Kindly Consider the following
11.
Kindly Consider the following
13.
Kindly Consider the following
14.
c
Kindly Consider the following
15.
Kindly Consider the following
16.
Kindly Consider the following
17.
Kindly Consider the following
18.
Kindly Consider the following
19.
Kindly Consider the following
20.
Choose the correct answer in Exercises 21 and 22.
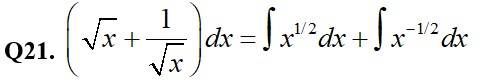
C
? The correct Answer is (C)
Kindly Consider the following
22.
Now,
Therefore, correct answer is A.
Kindly Consider the following
23.
Kindly Consider the following
25.
Kindly Consider the following
26.
Kindly go through the solution
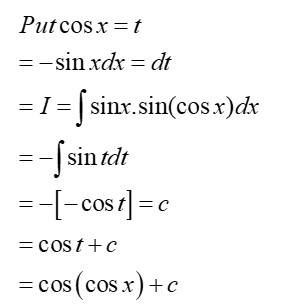
Kindly Consider the following
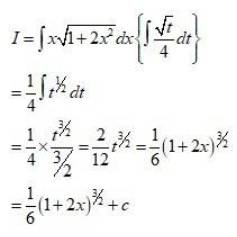
Kindly Consider the following
31.
Kindly go through the solution
Kindly Consider the following
33.
Kindly go through the solution
Kindly Consider the following
34.
Kindly Consider the following
35.
Kindly Consider the following
37.
Kindly Consider the following
38.
Kindly Consider the following
39.
Kindly Consider the following
40.
Kindly Consider the following
43.
Kindly Consider the following
44.
Kindly Consider the following
45.
Kindly go through the solution

Kindly Consider the following
46.
Kindly Consider the following
47.
Kindly Consider the following
48.
Kindly go through the solution
Kindly Consider the following
49.
Kindly go through the solution
Kindly Consider the following
50.
Kindly go through the solution
Kindly Consider the following
51.
Kindly Consider the following
52.
Kindly Consider the following
53.
Kindly Consider the following
54.
Kindly Consider the following
55.
Kindly Consider the following
56.
Kindly go through the solution
Kindly Consider the following
57.
Kindly Consider the following
58.
Kindly Consider the following
59.
From (1), we get
Kindly Consider the following
155.
Putting x = tanθ tan-1x = θ dx = sec2θdθ we get,

Kindly Consider the following
62.
Kindly Consider the following
63.
Kindly Consider the following
64.
Kindly Consider the following
65.
Kindly Consider the following
66.
Kindly Consider the following
67.
Kindly Consider the following
68.
Kindly Consider the following
69.
Kindly Consider the following
78.
Kindly Consider the following
80.
Kindly Consider the following
84.
Kindly Consider the following
86.
89. Kindly Consider the following
Kindly go through the solution
Kindly Consider the following
90.
Kindly Consider the following
91.
92. Kindly Consider the following
Kindly go through the solution
93. Kindly Consider the following
Kindly go through the solution
94. Kindly Consider the following
Kindly go through the solution
95. Kindly Consider the following
Kindly go through the solution
Kindly Consider the following
96.
97. Kindly Consider the following
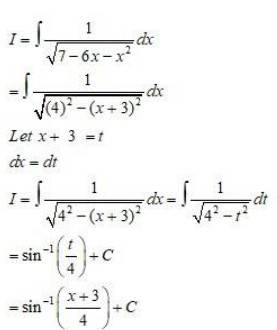
98. Kindly Consider the following
Kindly go through the solution
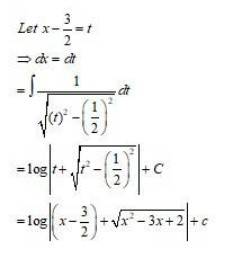
99. Kindly Consider the following
Kindly go through the solution
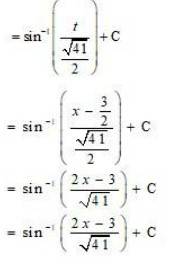
100. Kindly Consider the following
Kindly go through the solution
101. Kindly Consider the following
Kindly go through the solution
102. Kindly Consider the following
Kindly go through the solution

104. Kindly Consider the following
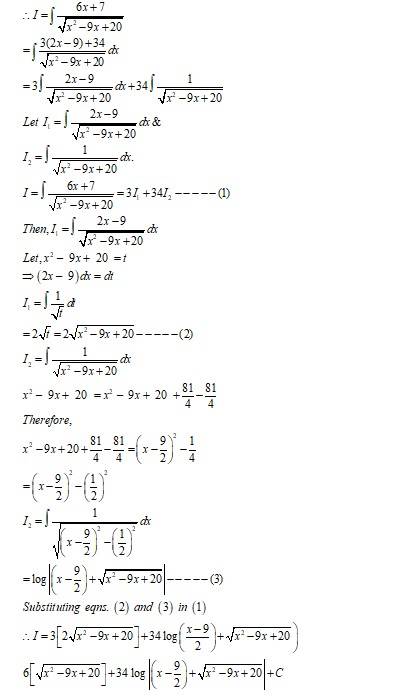
105. Kindly Consider the following
Kindly go through the solution
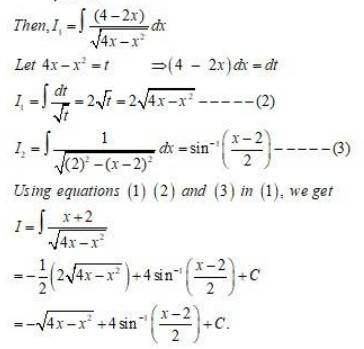
106. Kindly Consider the following
Kindly go through the solution
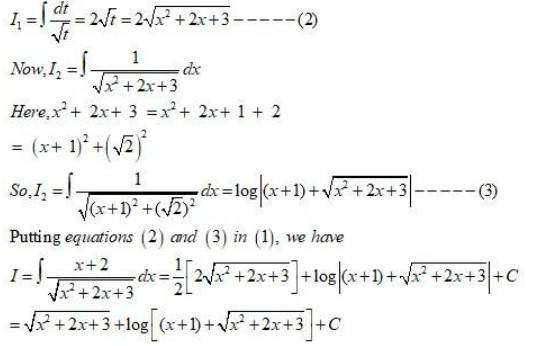
Kindly Consider the following
107.
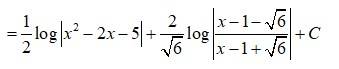
108. Kindly Consider the following
Kindly go through the solution

Kindly Consider the following
109.
110. Kindly Consider the following
Kindly go through the solution
111.
Kindly go through the solution
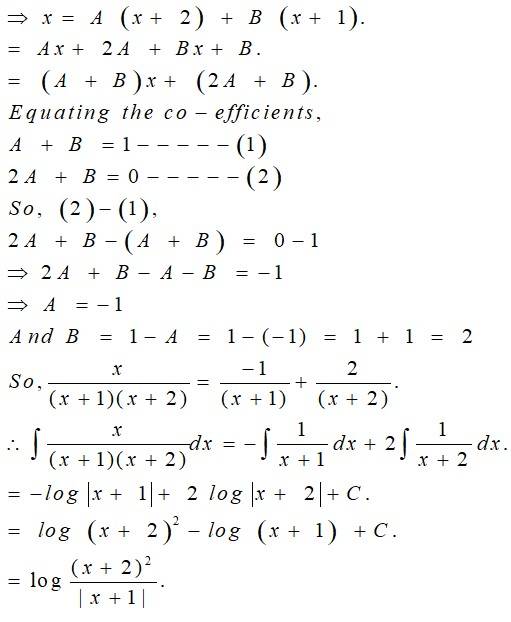
Kindly Consider the following
112.
Kindly go through the solution

Kindly Consider the following
113.
Kindly go through the solution

Kindly Consider the following
114.
Kindly go through the solution


Kindly Consider the following
115.
2x = A(x + 2) + B(x + 1).
= (A + B) x + (2A + B).
Comparing the coefficients we get,
A + B = 2 ---(1)
2A + B = 0 ---- (2).
So, Eqn (2) - (1),
2A + B - (A + B) = 0 - 2
Þ A = - 2
And B = 2 - A = 2 - (-2) = 2 + 2 = 4
B = 4
Kindly Consider the following
116.
which is not a proper fraction
So, division is missing
=> 2 -x = A(1 - 2x) + B x.
So, - 2A + B = - 1
A = 2.
So, B = - 1 + 2A = - 1 + 2 ´ 2 = - 1 + 4 = 3
Kindly Consider the following
117.
=> x = (Ax + B)(x- 1) + C(x2 + 1)
= Ax2- Ax + Bx- B + Cx2 + C.
Comparing the co-efficients we get,
A + C = 0 ---- (1)
- A + B = 1 ---- (2)
- B + C = 0 ---- (3)
Adding (1) and (2) we get,
A + C - A + B = 0 + 1
=> B + C = 1 --- (4)
Adding (4) + (3) we get,
- B + C + B + C = 0 + 1
=> 2C = 1
And C = B from (3)
So, from Eqn (1),
A = - C
Kindly Consider the following
118.
= A(x- 1)(x + 2) + B(x + 2) + C(x- 1)2
= A(x2 + 2x-x- 2) + B(x + 2) + C(x2 + 1 - 2x)
= A(x2 + x- 2) + B(x + 2) + C(x2- 2x + 1)
Comparing the co-efficient we get, A + C = 0 ¾ (1)
A + B - 2C = 1 ¾ (2)
- 2A + 2B + C = 0 ¾ (3)
EQn (3) - 2 ´ enQ. (2),
- 2A + 2B + C (2A + 2B - 4C) = 0 - 2 ´ 1.
=> - 4A + 5C = - 2 ¾ (4)
Eqn (4) + 4 ´ Eqn (1) we get,
- 4A + 5C + 4A + 4C = - 2 + 4 ´ 0
=> 9C = - 2

Kindly Consider the following
119.
Kindly go through the solution

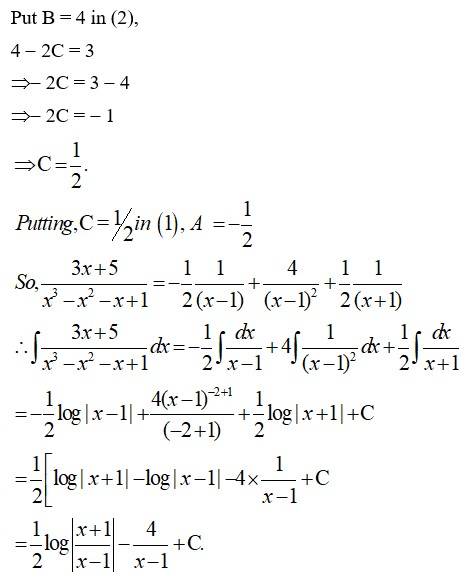
Kindly Consider the following
120.
Kindly go through the solution
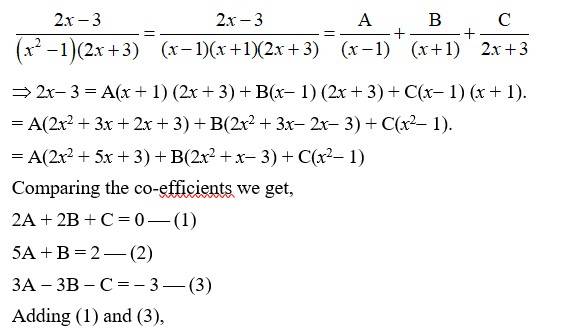

Kindly Consider the following
121.
Kindly go through the solution


Kindly Consider the following
122.
Kindly go through the solution
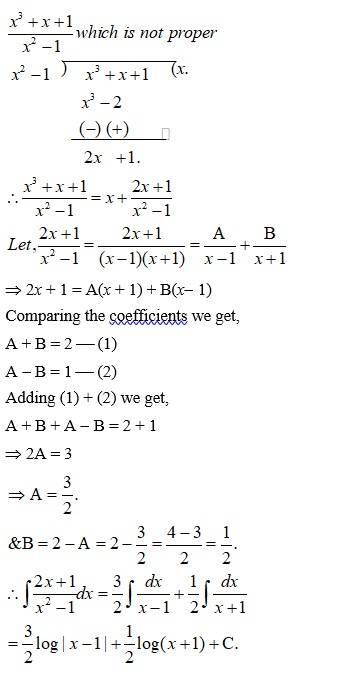
Kindly Consider the following
123.
Kindly go through the solution
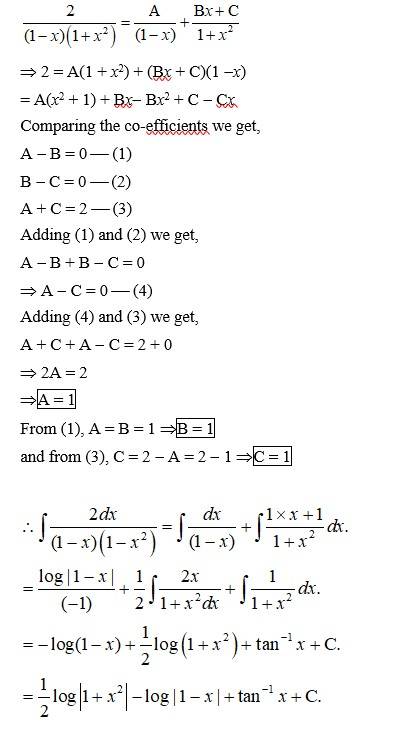
Kindly Consider the following
124.
Kindly go through the solution
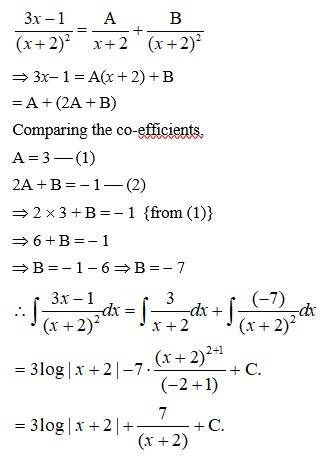
Kindly Consider the following
125.
Kindly go through the solution

Kindly Consider the following
126.
Putting xn = t Þ n xn- 1dx = dt
Kindly Consider the following
127.
Putting sin x = t cos xdx = dt
Kindly Consider the following
128.
Kindly go through the solution
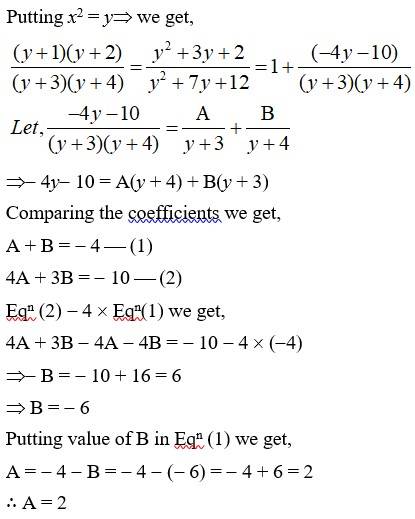
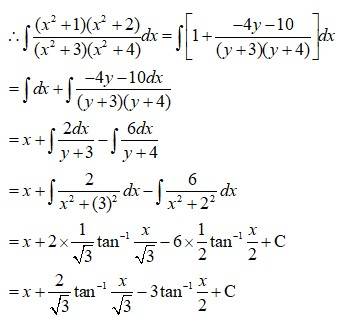
Kindly Consider the following
129.
Putting x2 = t such that 2xdx = dt
Kindly Consider the following
130.
Putting x4 = tÞ 4x3dx = dt
Kindly Consider the following
131.
Putting ex = t so that ex dx = dt=>dx =
Kindly Consider the following
132.
Kindly go through the solution
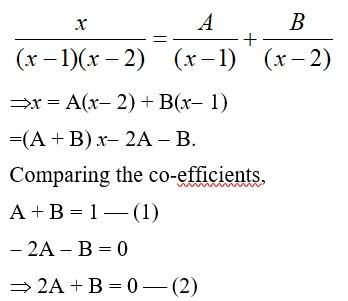

Kindly Consider the following
133.
Kindly Consider the following
134.
Kindly Consider the following
135.
Kindly Consider the following
136.
Kindly Consider the following
137.
Kindly Consider the following
138.
Kindly Consider the following
139.
Kindly Consider the following
140.
Kindly go through the solution
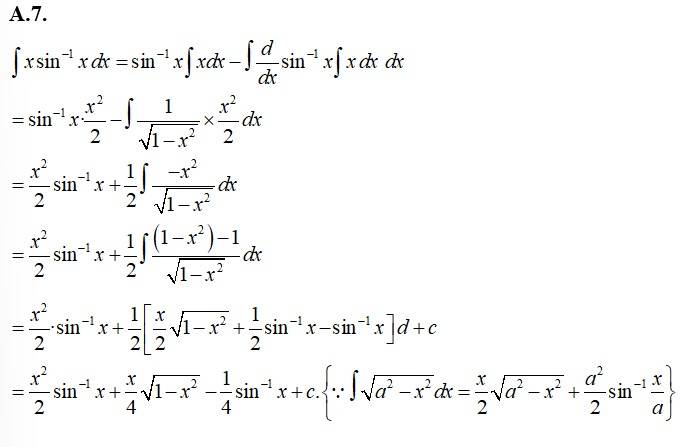
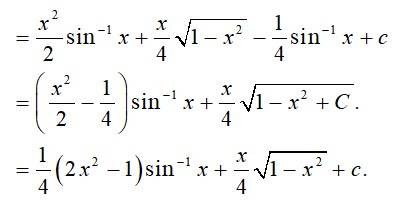
Kindly Consider the following
141.
Kindly Consider the following
142.
Putting cos-1 x =θ=> x = cosθ=>dx = - sinθdθ.
{θsin 2θ = 2 sinθ cosθ}
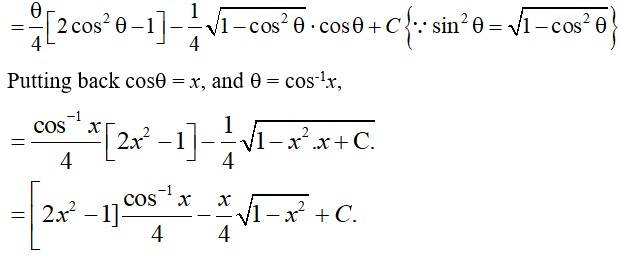
Kindly Consider the following
143.
Putting sin-1x =θ=> x = sinθ, dx = cosθdθ.

Kindly Consider the following
146.
Kindly Consider the following
147.
Kindly Consider the following
148.
Kindly Consider the following
149.
∴f (x) = sin x
f (x) = cos x.
ex [f (x) + f (x)] dx = exf (x) + C
Kindly Consider the following
150.
is of the form
ex [f(x) + f(x)] dx
Kindly Consider the following
151.
{∴ sin 2x = 2sin x cos x. cos 2x = cos- 2x- 1 1 + cos 2x = 2cos2x.
is in the form
ex [f(x) + f(x)].dx where
Kindly Consider the following
152.
So, I = exf (x) + C
Kindly Consider the following
153.
Kindly Consider the following
154.
Kindly Consider the following
156.
So, option (A) is correct.
Kindly Consider the following
157.
Kindly go through the solution
158. Kindly Consider the following
Kindly go through the solution
159. Kindly Consider the following
Kindly go through the solution
160. Kindly Consider the following
Kindly go through the solution
161. Kindly Consider the following
Kindly go through the solution
162. Kindly Consider the following
Kindly go through the solution
163. Kindly Consider the following
Kindly go through the solution
164. Kindly Consider the following
Kindly go through the solution
165. Kindly Consider the following
Kindly go through the solution
166. Kindly Consider the following
Kindly go through the solution
167. Kindly Consider the following
Kindly go through the solution
168. Kindly Consider the following
Kindly go through the solution
Kindly Consider the following
169.
We know that
where
Here, a = a, b= b and f(x) = x
Kindly Consider the following
170.
We know that
where nh = b - a
Here, a = 0, b = 5, nh = 5 and f(x) = x + 1
Kindly Consider the following
171.
We know that
where nh = b - a
Here, a = 2, b = 3, nh = 1 and f(x) = x2
Kindly Consider the following
172.
We know that
where nh = b - a
Here, a = 1, b = 4, nh = 3 and f(x) = x2 - xf(x) = x2 - x
Kindly Consider the following
173.
We know that
where nh = b - a
Here, a = -1, b = 1, nh = 2 and f(x) = ex
[ The series within brackets is a G.P. and ]
Kindly Consider the following
174.
We know that
where nh = b - a
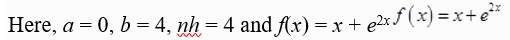
Kindly Consider the following
175.
Kindly Consider the following
176.
Kindly Consider the following
177.
Kindly Consider the following
178.
Kindly Consider the following
179.
Kindly Consider the following
180.
Kindly Consider the following
181.
Kindly go through the solution
Kindly Consider the following
182.
Kindly go through the solution
Kindly Consider the following
183.
Kindly go through the solution
Kindly Consider the following
184.
Kindly Consider the following
185.
Kindly Consider the following
186.
Kindly go through the solution
Kindly Consider the following
187.
Kindly Consider the following
188.
Kindly go through the solution
Kindly Consider the following
189.
When,
x = 0, t = 0
x = 1, t = 1
Kindly Consider the following
190.
Kindly go through the solution

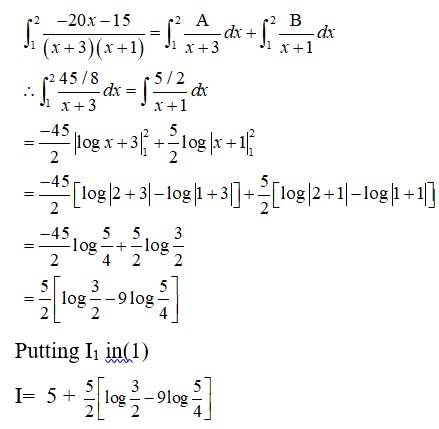
Kindly Consider the following
191.
Kindly go through the solution
Kindly Consider the following
192.
Kindly go through the solution
Kindly Consider the following
193.
Kindly Consider the following
194.
Kindly go through the solution
Kindly Consider the following
195.
Kindly go through the solution
Kindly Consider the following
196.
? Option (c) is correct.
228.

So,
= log |x| + log log |1 + x|
=
=
=
229. Kindly Consider the following
Kindly go through the solution
230. Kindly Consider the following
Kindly go through the solution
231.
Let I =
= =
=
=
Putting
I =
=
=
=
232.
Let I =
Putting x = t6. dx = 6t5dt.
I =
=
=
=
=
=
233.

From (1), B = - A =
From (2) C = 5 - B = 5
234.
Let x- a = t=> dx = dt.
Where C1 = C - a cos a
235.
236. Kindly Consider the following
Kindly go through the solution
237.
238.
239. Kindly Consider the following
Kindly go through the solution
240.
Let I
Putting ex = t=>exdx = dt.
241.
Let I =
Putting x2= y then,
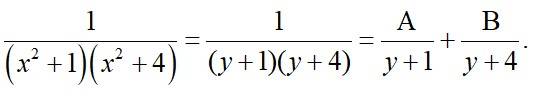
1 - A (y + 4) + 1B (y + 1)
Comparing the co-efficient,
A + B = 0 _____ (1)
4A + B = 1 ______ (2)
Equation (2) - (1),
4A + B - A - B = 1 - 0
3A = 1 =>A =
and B = - A = -
242.
Let I =
Putting cos x = t =>-sin x dx = dt =>sin x dx = -dt.
243.
Let I
244.
Let I
Putting f (ax + b) = t.
af' (ax + b) dx = dt
245. Kindly Consider the following
Kindly go through the solution

246. Kindly Consider the following
Kindly go through the solution

247. Kindly Consider the following
Kindly go through the solution
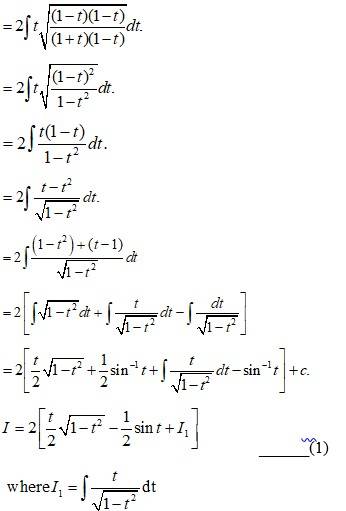
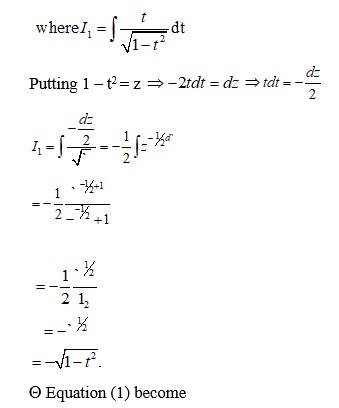
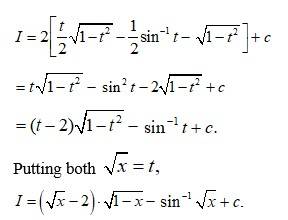
248.
Let I =
is in the form
249.
Let
The integrate is of form,
Comparing the co-efficients,
A + C = 1 ..........(1)
3A + B + C = 1 ..........(2)
2A + 2B + C = 1 .........(3)
Equation. (2) – 2 × Equation (1),
A + B = –1 .......(4)
Equation (3) - (1),
2A + 2B + C = A – C = 1 – 1
A + 2B = 0 ........(5)
Equation (5) - Equation (4),
A + 2B - A - B = 0 - (-1)
B = 1.
From (4), A = -1 - B = -1 - 1 = -2.
And from (1), C = 1 - A = 1 - (–2) = 1+2=3
250. Kindly Consider the following
Kindly go through the solution
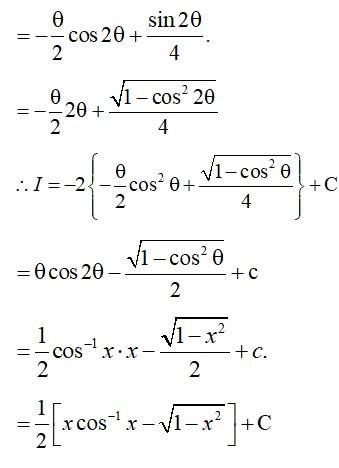
252.
Let I =
=
=
= –
=
=
=
=
=
253.
Let I =
=
=
=
=
Putting tan2x = t =>2 tan x?sec2xdx = dt
When x = 0, t = tan2x = tan2 0 = 0
x = t = tan2 = 12 = 1.
? I =
=
=
254.
=
=
=
=
=
=
=
=
=
=
where I1 =
Putting 2tan x = t =>2 sin2xdx = dt& when x = 0, t = 2 tan (0) = 0
x = , t = 2 tan = ∞
I1 =
=
= tan–1 (∞) – tan–10
= =
? I =
255. Kindly Consider the following
Kindly go through the solution
256. Kindly Consider the following
Kindly go through the solution
257.
Let I =
Let sin x – cos x = t. =>(cosx + sin x) dx = dt.
and (sin x – cos x)2 = t2
sin2x + cos2x – 2 sin x cos x = t2
1 – sin2x = t2.
sin2t = 1 - t2.
When x = 0, t = sin 0 – cos 0 = –1
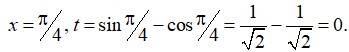
? I =
=
=
=
=
=
=
=
=
=
=
=
=
258.
Let I =
=
Putting sin x = t =>cos xdx = dt.
whenx = 0, t = sin 0 = 0.
? I =
=
=
=
=
=
=
=
259
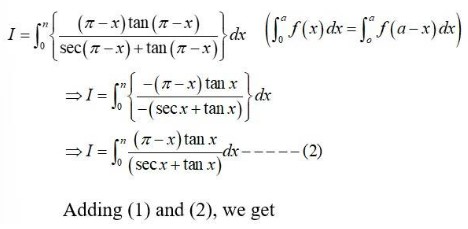
260.
Let I =
I =
I = I1 + I2 + I3______(1)
So, I1 = |x – 1| dx .
=
=
=
I2 =
=
=
=
=
=
=
I3 =
=
=
=
=
=
Hence Equation (1) becomes
I =
I =
261.
Let
The integrand is of the form.
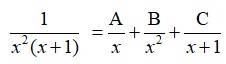
1 = Ax (x + 1) + B (x + 1) + Cx2
= A (x2 + x) + B (x + 1) + Cx2
Comparing the coefficients,
A + C = 0 ____ (1)
A + B = 0 ______ (2)
B = 1 ________ (3)
Putting Equation (3) in (2),
A + 1 = 0
A = -1.
and putting value of A in Equation (1),
-1 + C = 0
C = 1
Hence proved.
262.
LHS=
= e-e + e0
= e0 = 1=RHS
263.
Here f (x) = x17 cos4x
f ( -x) = ( -x)17 cos4 ( -x)
= -x17 cos4x
= f (x)
i e, odd fxn
As for odd fxn
therefore, I = 0.
264.
LHS = I
265.
Let I
Where I
Let tan x = t =>sec2xdx = dt
When, x = 0, t = tan 0. = 0
So, Equation (1) becomes,
=1 - log 2.
266.
Kindly go through the solution
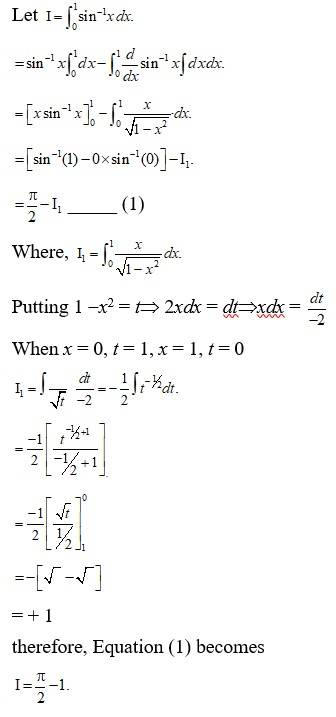
267. Evaluate as a limit of a sum.
Let
We know that,
Where,
Here, and
268. is Equal to
Let
Putting ex = t
exdx = dt.
= tan- 1 t + c
= tan- 1 (ex) + c
therefore, Option A is correct.
269. is Equal to
Let
So, option B is correct.
270. If is Equal to
Giver, f(a + bx) = f(x). _________ (1)
Let I
___________ (3) {because Equation (1)}
therefore, Option D is correct.
271. The value of is
A.1
B. 0
C.-1
D.
Consider,
Adding (1) and (2), we get
Thus, the correct option is B.
Maths Ncert Solutions class 12th Exam