2. Show that the relation R in the set R of real numbers, defined as R = {(a, b): a ≤ b2} is neither reflexive nor symmetric nor transitive.

We have, R= {(a,b):a≤b2} is a relation in R. For a∈R then is b=a,a≤a2 is not true for all real number less than 1. Hence, R is not reflexive. Let (a,b)∈R and a=1 and b=2 Then, a≤b2 = 1≤22 = 1≤4 so, (1,2)∈R But (b,a)=(2,1) i.e., 2≤12 = 2≤1 is not true so, (2,1)∉R hence, R is not symmetric. For, (a,b)=(10,4)&(b,c)=(4,2)∈R We have, a=10≤42=b2 => 10≤16 is true So, (10,4)∈R And 4≤22 => 4≤4 So, (4,2)∈R But 10≤22 => 10≤4 is not true. So, (10,2)∉R Hence, R is not transitive.

Let f : R → R be defined as where a, b, c ∈ R and [t] denotes greatest integer less than or equal to t. Then, which of the following statements is true?

If f is discontinuous at exactly one point, then a + b + c ≠  1

There exists a, b, c ∈  R such that f is continuous on R.

If f is discontinuous at exactly one point, then a + b + c = 1.

f is discontinuous at atleast two points, for any values of a, b and c

Let p, q, r be three logical statements. Consider the compound statements S 1 : ( ( ∼ p ) ∨ q ) ∨ ( ( ∼ p ) ∨ r ) a n d S 2 : p → ( q ∨ r ) Then, which of the following is NOT true?

If S 2 is False, then S 1 is True

If S 2 is True, then S 1 is True

If S 2 is False, then S 1 is False

If S 1 is False, then S 2 is False

Class 12 Maths Chapter 1 NCERT Solutions: Relations and Functions Explained

Q: 9. Show that each of the relation R in the set A = {x ∈ Z: 0 ≤ x ≤ 12} ,given by: (i) R = { (a,b) : |a - b| is a multiple of 4} (ii) R = { (a,b) : a= b} is an equivalence relation. Find the set of all elements related to 1 in each case.

We have, A= {x∈2,0≤x≤12} The relation in set A is defined by R= { (a,b):|a−b| is a multiple of 4} For all a∈A , |a−a|=0 is a multiple of 4 So, (a,a)∈R i.e., R is reflexive For a,b∈A&(a,b)∈R we have, |a−b| is multiple of 4 |−(b−a)| is multiple of 4 |b−a| is multiple of 4 So, (b,a)∈R i.e., R is symmetric for a,b,c∈A &(a,b)∈R&(b,c)∈R |a−b| & |b−c| is a multiple of 4 So |a−b|+|b−c| is also a multiple of 4 |a−b+b−c| is a multiple of 4 |a−c| is a multiple of 4 So, (a,c)∈R i.e., R is transitive Hence, R is an equivalence relation. Finding all set of elements related to 1 For a∈A Then, (a,1)∈R i.e., |a−1| is a multiple of 4 So, a can be 0 ≤ a ≤ 12 Only, |1−1|=0 |5−1|=4 is a multiple of 4 |9−1|=8 Hence, sets of elements related to A= {1,5,9} The relation in set A is defined as R= {(a,b):a=b} For all a∈A , a=a is true so, (a,a)∈R i.e., R is reflexive for a,b∈A&(a,b)∈R we have, a=b b=a i.e., (b,a)∈R so, R is symmetric for a,b,c∈A , (a,b)∈R and (b,c)∈R . We have, a=b and b=c a=c i.e., (a,c)∈R ∴ R is transitive Hence, R is an equivalence relation Find all sets of elements related to 1 For a∈A , we need (a,1)∈R i.e., a=1 so, set of elements related to 1 in A is {1}.

Q: 27. Let f: R → R be defined as f(x) = x4. Choose the correct answer. (A) F is one-one onto (B) F is many-one onto (C) F is one-one but not onto (D) F is neither one-one nor onto

Given, f:R→R defined by f (x)=x4 For x1, x2∈R such that f (x1)=f (x2) ⇒x14=x24 ⇒x1=±x2 ⇒x1=x2 or x1=−x2 So, f is not one-one The range of f (x) is a set of all positive real numbers which is not equal to co-domain R So, f in not onto ∴ Option (D) is correct

Updated on Jul 30, 2025 17:37 IST

By Pallavi Pathak, Assistant Manager Content

Relations and Functions Class 12 NCERT Solutions cover different types of relations and functions, invertible functions, composition of functions, and binary operations. The chapter builds the foundation for higher levels of Mathematics. It explores the definitions and types of relations and functions. The concepts covered in this chapter are important for understanding advanced topics like calculus, inverse trigonometric functions, and probability.
The Relations and Functions Class 12 solutions help students to understand the concepts clearly and solve the questions in exams. It is ideal for the CBSE board exam preparation and for preparing for other entrance tests like NEET and JEE Mains.
To get access to the NCERT solutions of Class 11 and Class 12 subjects - Physics, Chemistry, and Maths, and get the key topics and free PDFs of all the chapters, find them here.

Table of content

Glance at Class 12 Maths Chapter 1 Solutions
Class 12 Maths Relations and Functions: Key Topics, Weightage
Important Formulas of Relations and Functions Class 12
Class 12 Math Chapter 1 Relation and Function Solution PDF
Class 12 Math Relation and Function Exercise -wise solutions
Maths Class 12 Relation and Function Exercise 1.1 Solutions

Glance at Class 12 Maths Chapter 1 Solutions

Here is a walkthrough of the Class 12 Maths Chapter 1 Solutions:

It includes the different types of relations and equivalence relations, invertible functions, composition of functions, and binary operations.
$Empty relation is the relation R in X given by R = \emptyset \subseteq X \times X$
$Symmetric relation R in X is a relation satisfying (a, b) \in R implies (b, a) \in R$
$Universal relation is the relation R in X given by R = X \times X$
$Reflexive relation R in X is a relation with (a, a) \in R \forall a \in X$
$A function f : X \to Y is one-one and onto (or bijective), if f is both one-one and onto$
$A function f : X \to Y is onto (or surjective), if given any y \in Y, \exists x \in X such that f (x) = y .$

If you are looking for chapter-wise Class 12 Maths NCERT Solutions with all important topics and a free PDF, then find them here.

Class 12 Maths Relations and Functions: Key Topics, Weightage

Class 12 Maths Chapter 1 Solutions is important for students as it forms the base for many other concepts. See below the topics covered in this chapter:

Exercise	Topics Covered
1.1	Introduction
1.2	Types of Relations
1.3	Types of Functions
1.4	Composition of Functions and Invertible Function

Relations and Functions Class 12 Weightage in JEE Mains

Exam	Weightage
JEE Mains	3.3% to 5%

Class 12 Math Chapter 1 Relation and Function Solution PDF

Find below the free Relations and Functions Class 12 PDF. Download the PDF to prepare well for the CBSE Board exams and other competitive exams like JEE Mains.
Class 12 Math Chapter 1 Relations and Functions Solution: Free PDF Download

Class 12 Math Relation and Function Exercise -wise solutions

We have covered all important topics, such as the type of relation, symmetric and asymmetric relations, functions, bijective functions, and surjective functions in class 12 relations and functions exercises. Students will get problems related to different concepts and properties of relations and functions in the exercises. Candidates can check the exercise-wise chapter 1 math solutions below;

Maths Class 12 Relation and Function Exercise 1.1 Solutions

Chapter 1 Relation and Function Exercise 1.1 focuses on problems based on identifying reflexive, symmetric, and transitive relations & checking whether the relation is an equivalence relation or not. Class 12 Math Relation and Function Exercise 1.1 consists of 16 Questions (14 Short Answers, 2 MCQ). Students can check the complete the exercise 1.1 solutions below;

Relation and Function exercise 1.1 solutions

Q1. Determine whether each of the following relations are reflexive, symmetric and transitive:

(i)Relation R in the set A = {1, 2, 3…13, 14} defined as

R = {(x, y): 3x − y = 0}

(ii) Relation R in the set N of natural numbers defined as

R = {(x, y): y = x + 5 and x < 4}

(iii) Relation R in the set A = {1, 2, 3, 4, 5, 6} as

R = {(x, y): y is divisible by x}

(iv) Relation R in the set Z of all integers defined as

R = {(x, y): x − y is as integer}

(v) Relation R in the set A of human beings in a town at a particular time given by

(a) R = {(x, y): x and y work at the same place}

(b) R = {(x, y): x and y live in the same locality}

(d) R = {(x, y): x is wife of y}

(e) R = {(x, y): x is father of y}

A.1. (i) We have, $R = {(x, y) : 3 x - y = 0}$ a relation in set A= ${1, 2, 3 . . . . . . . . . . 14}$

For $x \in A, y = 3 x$ or $y \neq x$ i.e.,

$(x, x)$ does not exist in R

$∴$ R is not reflexive.

For $(x, y) \in R, y = 3 x$

Then $(y, x) x \neq 3 y$

So $(y, x) \notin R$

$∴$ R is not symmetric

For $(x, y) \in R$ and $(y, z) \in R$ . We have

$y = 3 x$ and $z = 3 y$

Then $z = 3 (3 x) = 9 x$

i.e., $(x, z) \notin R$

$∴$ R is not Transitive

(ii) We have,

R= ${(x, y) : y = x + 5 & x < 4}$ is a relation in N

= ${(1, 1 + 5), (2, 2 + 5), (3, 3 + 5)}$

= ${(1, 6), (2, 7), (3, 8)}$

Clearly, R is not reflexive as $(x, x) \notin R$ and $x < 4 & x \in N$

Also, R is not symmetric as $(1, 6) \in R$ but $(6, 1) \notin R$

And for $(x, y) \in R (y, z) \notin R$ . Hence, R is not Transitive.

(iii) R= ${(x, y); y$ is divisible by x $}$ is a relation in set

A= ${1, 2, 3, 4, 5, 6}$

So, R= ${(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (5, 5), (6, 6)}$

Hence, R is reflexive because $(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6) \in R$ i.e., $(x, x) \in R$

R is not symmetric as $(1, 2) \in R$ but $(2, 1) \notin R$

And for $x, y, z \in A$ and $(x, y) \in R & (y, z) \in R$

$\frac{y}{z} = n$ and $\frac{z}{y} = m$ where $n & m \in N$

Then, $z = m y = m (n x) = m n . x$

$\frac{z}{x} = m . n, m, m n \in N$

Hence, $(x, z) \in R$

$∴$ R is transitive

(iv) R= ${(x, y) : x - y$ is an integer $}$ is a relation in set Z

For $x \in Z$

$x - x = 0$ is an integer

So, $(x, x) \in R$ i.e., R is reflexive

For $x, y \in Z$ and $(x, y) \in R$

$x - y$ is an integer

$- (y - x)$ is an integer

$(y - x)$ is an integer

So, $(y, x) \in R$ i.e., R is symmetric

For $x, y, z \in R$ and $(x, y) \in R & (y, z) \in R$ We have,

$x - y$ is an integer

$y - z$ is an integer

So, $(x - y) + (y - z)$ is also an integer

$x - z$ is an integer

So, $(x, z) \in R$ i.e., R is transitive.

(v) (a) R= ${(x, y) : x$ and $y$ work at same place $}$ in set A of human being.

For $x \in A$ we get

$x & x$ work at same place

$(x, x) \in R$ So, R is reflexive.

For $x, y \in A$ and $(x, y) \in R$ We get,

$x & y$ work at same place

$y & x$ work at same place

$(y, x) \in R$ . So, R is symmetric.

For $x, y, z \in A$ and $(x, y)$ and $(y, z) \in R$ . We have,

$x & y$ work at same place

$y & z$ work at same place

$x & z$ work at same place

i.e., $(x, z) \in R$ . So, R is Transitive.

(b) R= ${(x, y) : x & y$ live in same locality $}$

For $x \in A$ , we get,

$x & x$ live in same locality

$(x, x) \in R$ So, R is reflexive.

For $x, y \in A$ and $(x, y) \in R$ we get,

$x & y$ live in same locality

$y & x$ live in same locality

i.e., $(y, x) \in R$ . So, R is symmetric.

For $x, y, z \in A$ and $(x, y)$ & $(y, z) \in R$ . Then

$x, y$ live in same locality

$y, z$ live in same locality

$x, z$ live in same locality

So, $(x, z) \in R$ i.e., R is transitive.

For $x \in A$ ,

Height $(x) \neq 7 +$ height of $(x)$

So, $(x, x) \notin R$ . i.e., R is not reflexive.

For, $x, y \in A$ and $(x, y) \in R$ we have,

Height $(x)$ $= 7 + h e i g h t (y)$

But $h e i g h t (y) \neq 7 + h e i g h t (x)$

So, $(y, x) \in R$ i.e., R is not symmetric.

For $x, y, z \in A$ and $(x, y) \in R$ and $(y, z) \in R$ we have,

Height $(x) = 7 + h e i g h t (y)$

And $h e i g h t (y) = 7 + h e i g h t (z)$

So, $h e i g h t (x) = 7 + 7 + h e i g h t (z) = 14 + h e i g h t (z)$

i.e., $(x, z) \notin R$

So, R is not transitive.

(d) R= ${(x, y) : x$ is wife of y $}$

For $x \in A,$

X is not wife of x.

So, $(x, x) \notin R$ i.e., R is not reflexive.

For $x, y \in A$ and $(x, y) \in R$ ,

X is wife of y but y is not wife of x

So, $(y, x) \notin R$ . i.e., R is not symmetric.

For $x, y, z \in A$ and $(x, y)$ and $(y, z) \in R$

X is wife of y

Y is wife of z

But y can never be husband & wife simultaneously

So, R is not transitive.

(e) R= ${(x, y) : x$ is father of y $}$

For $x \in A$ ,

X is not a father of x

So, $(x, x) \notin R$ i.e., R is not reflexive.

For $x, y \in A$ and $(x, y) \in R$

X is father of y

Y is father of z

But x is not father of z

So, $(x, z) \notin R$ i.e., R is not transitive.

Q2. Show that the relation R in the set R of real numbers, defined as

R = {(a, b): a ≤ b²} is neither reflexive nor symmetric nor transitive.

A.2. We have,

R= ${(a, b) : a \leq b^{2}}$ is a relation in R.

For $a \in R$ then is $b = a, a \leq a^{2}$ is not true for all real number less than 1.

Hence, R is not reflexive.

Let $(a, b) \in R$ and a=1 and b=2

Then, $a \leq b^{2}$ = $1 \leq 2^{2}$ = $1 \leq 4$ so, $(1, 2) \in R$

But $(b, a) = (2, 1)$

i.e., $2 \leq 1^{2}$ = $2 \leq 1$ is not true

so, $(2, 1) \notin R$

hence, R is not symmetric.

For, $(a, b) = (10, 4) & (b, c) = (4, 2) \in R$

We have, $a = 10 \leq 4^{2} = b^{2}$ => $10 \leq 16$ is true

So, $(10, 4) \in R$

And $4 \leq 2^{2}$ => $4 \leq 4$ So, $(4, 2) \in R$

But $10 \leq 2^{2}$ => $10 \leq 4$ is not true.

So, $(10, 2) \notin R$

Hence, R is not transitive.

Q3. Check whether the relation R defined in the set {1, 2, 3, 4, 5, 6} as

R = {(a, b): b = a + 1} is reflexive, symmetric or transitive.

A.3. We have,

R= ${(a, b) : b = a + 1}$ is a relation in set ${1, 2, 3, 4, 5, 6}$

So, R= ${(1, 2), (2, 3), (3, 4), (4, 5), (5, 6), (6, 7)}$

As, $(1, 1) \notin R$ , R is not reflexive

As, $(1, 2) \in R$ but $(2, 1) \notin R$ , R is not symmetric

And as $(1, 2)$ & $(2, 3) \in R$ but $(1, 3) \notin R$

Hence, R is not transitive.

Q4. Show that the relation R in R defined as R = {(a, b): a ≤ b}, is reflexive and transitive but not symmetric.

A.4. We have, R= ${(a, b) : a \leq b}$ is a relation in R.

For, $a \in R$ ,

$a \leq b$ but $b \leq a$ is not possible i.e., $(b, a) \notin R$

Hence, R is not symmetric.

For $(a, b) \in R & (b, c) \in R$ and $a, b, c \in R$

$a \leq b$ and $b \leq c$

So, $a \leq c$

i.e., $(a, c) \in R$

$∴$ R is transitive.

Commonly asked questions

2. Show that the relation R in the set R of real numbers, defined as

R = {(a, b): a ≤ b²} is neither reflexive nor symmetric nor transitive.

We have,

R= ${(a, b) : a \leq b^{2}}$ is a relation in R.

For $a \in R$ then is $b = a, a \leq a^{2}$ is not true for all real number less than 1.

Hence, R is not reflexive.

Let $(a, b) \in R$ and a=1 and b=2

Then, $a \leq b^{2}$ = $1 \leq 2^{2}$ = $1 \leq 4$ so, $(1, 2) \in R$

But $(b, a) = (2, 1)$

i.e., $2 \leq 1^{2}$ = $2 \leq 1$ is not true

so, $(2, 1) \notin R$

hence, R is not symmetric.

For, $(a, b) = (10, 4) & (b, c) = (4, 2) \in R$

We have, $a = 10 \leq 4^{2} = b^{2}$ => $10 \leq 16$ is true

So, $(10, 4) \in R$

And $4 \leq 2^{2}$ => $4 \leq 4$ So, $(4, 2) \in R$

But $10 \leq 2^{2}$ => $10 \leq 4$ is not true.

So, $(10, 2) \notin R$

Hence, R is not transitive.

9. Show that each of the relation R in the set A = {x ∈ Z: 0 ≤ x ≤ 12} ,given by:

(i) R = { (a,b) : |a - b| is a multiple of 4}

(ii) R = { (a,b) : a= b} is an equivalence relation. Find the set of all elements related to 1 in each case.

We have,

A= ${x \in 2, 0 \leq x \leq 1 2}$

The relation in set A is defined by

R= { $(a, b) : | a - b |$ is a multiple of 4}

For all $a \in A$ ,

$| a - a | = 0$ is a multiple of 4

So, $(a, a) \in R$ i.e., R is reflexive

For $a, b \in A & (a, b) \in R$ we have,

$| a - b |$ is multiple of 4

$| - (b - a) |$ is multiple of 4

$| b - a |$ is multiple of 4

So, $(b, a) \in R$

i.e., R is symmetric

for $a, b, c \in A$ $& (a, b) \in R & (b, c) \in R$

$| a - b |$ & $| b - c |$ is a multiple of 4

So $| a - b | + | b - c |$ is also a multiple of 4

$| a - b + b - c |$ is a multiple of 4

$| a - c |$ is a multiple of 4

So, $(a, c) \in R$

i.e., R is transitive

Hence, R is an equivalence relation.

Finding all set of elements related to 1

For $a \in A$

Then, $(a, 1) \in R$ i.e., $| a - 1 |$ is a multiple of 4

So, a can be 0 ≤ a ≤ 12

Only,

$| 1 - 1 | = 0$

$| 5 - 1 | = 4$ is a multiple of 4

$| 9 - 1 | = 8$

Hence, sets of elements related to A= ${1, 5, 9}$

The relation in set A is defined as R= ${(a, b) : a = b}$

For all $a \in A$ ,

a=a is true

so, $(a, a) \in R$

i.e., R is reflexive

for $a, b \in A & (a, b) \in R$ we have,

a=b

b=a i.e., $(b, a) \in R$

so, R is symmetric

for $a, b, c \in A$ , $(a, b) \in R$ and $(b, c) \in R$ . We have,

a=b and b=c

a=c i.e., $(a, c) \in R$

$∴$ R is transitive

Hence, R is an equivalence relation

Find all sets of elements related to 1

For $a \in A$ , we need $(a, 1) \in R$

i.e., a=1

so, set of elements related to 1 in A is {1}.

27. Let f: R → R be defined as f(x) = x⁴. Choose the correct answer.

(A) F is one-one onto

(B) F is many-one onto

(C) F is one-one but not onto

(D) F is neither one-one nor onto

Given, $f : R \to R$ defined by $f (x) = x_{}^{4}$

For $x_{1}, x_{2} \in R$ such that $f (x_{1}) = f (x_{2})$

$\Rightarrow x_{1}^{4} = x_{2}^{4}$

$\Rightarrow x_{1}^{} = \pm x_{2}^{}$

$\Rightarrow x_{1}^{} = x_{2}^{}$ or $x_{1}^{} = - x_{2}^{}$

So, $f$ is not one-one

The range of $f (x)$ is a set of all positive real numbers which is not equal to co-domain $R$

So, $f$ in not onto

$∴$ Option (D) is correct

Kindly Consider the following

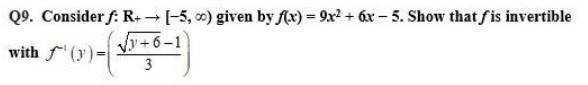
Kindly go through the solution

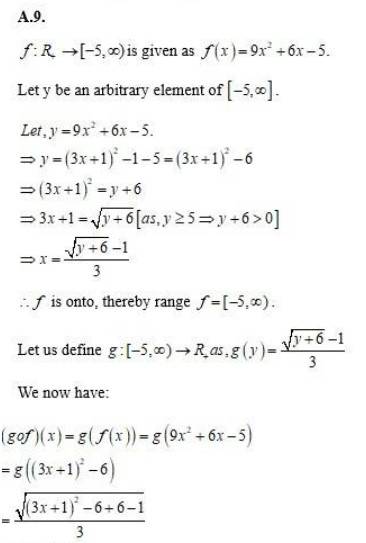
74. Number of binary operations on the set {a, b} are:

(A) 10

(B) 16

(C) 20

(D) 8

A binary operation * on {a, b} is a function from {a, b} × {a, b} → {a, b}

i.e., * is a function from { (a, a), (a, b), (b, a), (b, b)} → {a, b}.

Hence, the total number of binary operations on the set {a, b} is 2⁴ i.e., 16.

The correct answer is B.

26. Let A = R – {3} and B = R – {1}. Consider the function f : A → B defined by f(x) = (x-2/x-3) Is f one-one and onto? Justify your answer.

Given, $f : A \to B$ defined by $f (x) = (\frac{x - 2}{x - 3})$

Let $x_{1}, x_{2} \in A = R - {3}$ such that

$f (x_{1}) = f (x_{2})$

$\Rightarrow \frac{x_{1} - 2}{x_{1} - 3} = \frac{x_{2} - 2}{x_{2} - 3}$

$\Rightarrow (x_{1} - 2) (x_{2} - 3) = (x_{2} - 2) (x_{1} - 3)$

$\Rightarrow x_{1} x_{2} - 3 x_{1} - 2 x_{2} + 6 = x_{2} x_{1} - 3 x_{2} - 2 x_{1} + 6$

$\Rightarrow 2 x_{1} - 3 x_{1} = 2 x_{2} - 3 x_{2}$

$\Rightarrow - x_{1} = - x_{2}$

$\Rightarrow x_{1} = x_{}$

So, $f$ is one-one

For $y \in B = R - {1}$ there exist $f (x) = y$ such that

$\frac{x_{} - 2}{x_{} - 3} = y$

$\Rightarrow x - 2 = x y - 3 y$

$\Rightarrow x - x y = 2 - 3 y$

$\Rightarrow x (1 - y) = 2 - 3 y$

$\Rightarrow x = \frac{2 - 3 y}{1 - y}$ where $y \neq 1 . \in A$

Thus, $f (\frac{2 - 3 y}{1 - y}) = \frac{(\frac{2 - 3 y}{1 - y}) - 2}{(\frac{2 - 3 y}{1 - y}) - 3} = \frac{2 - 3 y - 2 + 2 y}{2 - 3 y - 3 + 3 y}$

$\Rightarrow \frac{- y}{- 1} = y$

$∴ f$ is onto

25. Let N → N be defined by f(n) for all

State whether the function f is bijective. Justify your answer.

Given, $f : N \to N$ defined $f (x) = (\begin{matrix} \frac{x + 1}{2}, i f & x i s o d d \\ \frac{x}{2}, i f & x i s e v e n \end{matrix})$ $\cup x \in N$

Let $x_{1} = 1$ and $x_{2} = 2 \in N,$

$f (x_{1}) = f (x_{2}) \Rightarrow f (1) = f (2)$

$\Rightarrow \frac{1 + 1}{2} = \frac{2}{2}$

$\Rightarrow 1 = 1$ but $1 \neq 2$

So, $f$ is not one-one

For $x =$ odd and $x \in N$ , say $x = 2 C + 1$ where $C \in N$

There exist $(4 C + 1)$ $\in N$ such that

$(4 C + 1) = \frac{4 C + 1 + 1}{2} = 2 C + 1 . \in N$

And for $x =$ even $\in N$ , say $x = 2 C$ where $C \in N$

There exist $(4 C) \in N$ such that

$f (4 C) = \frac{4 C}{2} = 2 C . \in N$

So, $f$ is onto

But, $f$ is not bijective

39. Consider f: {1, 2, 3} → {a, b, c} given by f(1) = a, f(2) = b and f(3) = c. Find f⁻¹ and show that (f⁻¹⁾⁻¹ = f.

$f (1) = a, f (2) b, a n d, f (3) = c$

If we define $g : {a, b, c} \to {1, 2, 3} a s, g (a) = 1, g (b) = 2, g (c) = 3,$ then we have:

$\begin{array}{l} (f o g) (a) = f (g (a)) = f (1) = a \\ (f o g) (b) = f (g (b)) = f (2) = b \\ (f o g) (c) = f (g (c)) = f (3) = c \\ A n d \\ (g o f) (1) = g (f (1)) = f (a) = 1 \\ (g o f) (2) = g (f (2)) = f (b) = 2 \\ (g o f) (3) = g (f (3)) = f (c) = 3 \\ ∴ g o f = I_{X} a n d, f o g = I_{Y} \\ W h e r e, X = {1, 2, 3}, a n d, Y = {a, b, c} . \end{array}$

Thus, the inverse of f exists and $f^{- 1} = g .$

$∴ f^{- 1} : {a, b, c} \to {1, 2, 3}$ is given by,

$\begin{array}{l} f^{- 1} (a) = 1, f^{- 1} (b) = 2, f^{- 1} (c) = 3 \end{array}$

Let us now find the inverse of $f^{- 1}$ i.e., find the inverse of g.

If we define $h : {1, 2, 3} \to {a, b, c} a s$

$h (1) = a, h (2) = b, h (3) = c$ , then we have

$\begin{array}{l} (g o h) (1) = g (h (1)) = g (a) = 1 \\ (g o h) (2) = g (h (2)) = g (b) = 2 \\ (g o h) (3) = g (h (3)) = g (c) = 3 \\ A n d \\ (h o g) (a) = h (g (a)) = h (1) = a \\ (h o g) (b) = h (g (b)) = h (2) = b \\ (h o g) (c) = h (g (c)) = h (3) = c \\ ∴ g o h = I_{X} a n d, h o g = I_{Y} \\ W h e r e, X = {1, 2, 3}, a n d, Y = {a, b, c} . \end{array}$

Thus, the inverse of g exists and $g^{- 1} = h \Rightarrow {(f^{- 1})}^{- 1} = h .$

It can be noted that h=f.

Hence, ${(f^{- 1})}^{- 1} = f .$

41. If $f : R \to R$ be given by $f (x) = {(3 - x^{3})}^{\frac{1}{3}}$ , then f of(x) is

(A) 1/x³

(B) x³

(C) x

(D) (3 − x³)

$f : R \to R$ is given as $f (x) = {(3 - x^{\land} 3)}^{\land} (1 / 3)$

$\begin{array}{l} f (x) = {(3 - x^{3})}^{\frac{1}{3}} \\ ∴ f o f (x) = f (f (x)) = f ({(3 - x^{3})}^{\frac{1}{3}}) = {[3 - {({(3 - x^{3})}^{\frac{1}{3}})}^{3}]}^{\frac{1}{3}} \\ = {[3 - (3 - x^{3})]}^{\frac{1}{3}} = {(x^{3})}^{\frac{1}{3}} = x \\ ∴ f o f (x) = x \end{array}$

The correct answer is C.

2. Check the injectivity and surjectivity of the following functions:

(i) f: N → N given by f(x) = x²

(ii) f: Z → Z given by f(x) = x²

(iii) f: R → R given by f(x) = x²

(iv) f: N → N given by f(x) = x³

(v) f: Z → Z given by f(x) = x³

(i) $f : N \to N$ given by $f (x) = x_{}^{2}$

For, $x_{1}, x_{2} \in N$ , $f (x_{1}) = f (x_{2})$

$\Rightarrow x_{1}^{2} = x_{2}^{2}$

$\Rightarrow x_{1}^{} = x_{2}^{} \notin N$

So, $f$ is one-one/ injective

For $x \in N$ , i.e., $x = 1, 2, 3 . . . .$

Range of $f (x) = {1_{}^{2}, 2_{}^{2}, 3_{}^{2} . . .} = {1, 4, 9 . . .} \neq N$

i.e., co-domain of $N$

So, $f$ is not onto/ subjective

(ii) $f : Z \to Z$ given by $f (x) = x_{}^{2}$

For, $x_{1}, x_{2} \in Z$ , $f (x_{1}) = f (x_{2})$

$\Rightarrow x_{1}^{2} = x_{2}^{2}$

$\Rightarrow x_{1}^{} = \pm x_{2}^{} \notin Z$

i.e., $x_{1} = x_{2}$ and $x_{1} = - x_{2}$

So, $f$ is not one-one/ injective

For $x \in Z$ , $x = 0, \pm 1, \pm 2, \pm 3 . . . .$

Range of $f (x) = {0_{}^{2}, {(\pm 1)}_{}^{2}, {(\pm 2)}_{}^{2}, {(\pm 3)}_{}^{2} . . .}$

${0, 1, 4, 9 . . . .} \neq$ co-domain $Z$

So, $f$ is not onto/ subjective

(iii) $f : R \to R$ given by $f (x) = x_{}^{2}$

For, $x_{1}, x_{2} \in R$ , $f (x_{1}) = f (x_{2})$

$\Rightarrow x_{1}^{2} = x_{2}^{2}$

$\Rightarrow x_{1}^{} = \pm x_{2}^{}$

So, $f$ is not injective

For $x \in R$

Range of $f (x) = {x_{}^{2}, x \in R}$ gives a set of all positive real numbers

Hence, range of $f (x \neq)$ co-domain of $R$

So, $f$ is not subjective

(iv) $f : N \to N$ given by $f (x) = x_{}^{3}$

For, $x_{1}, x_{2} \in N$ , $f (x_{1}) = f (x_{2})$

$\Rightarrow x_{1}^{3} = x_{2}^{3}$

$\Rightarrow x_{1}^{} = x_{2}^{} \in N$

So, $f$ is injective

For $x \in N,$

Range of $f (x) = {1_{}^{3}, 2_{}^{3}, 3_{}^{3} . . . .}$

${1_{}^{}, 8, 2 7_{}^{} . . . .} \neq$ co-domain of $N$

So, $f$ is not subjective

(v) $f : R \to R$ given by $f (x) = x_{}^{3}$

For, $x_{1}, x_{2} \in N$ , $f (x_{1}) = f (x_{2})$

$\Rightarrow x_{1}^{3} = x_{2}^{3}$

$\Rightarrow x_{1}^{} = x_{2}^{} \in N$

So, $f$ is injective

For $x \in R,$

Range of $f (x) = {1_{}^{3}, 2_{}^{3}, 3_{}^{3} . . . .}$

${1_{}^{}, 8, 2 7_{}^{} . . . .} \neq$ co-domain of R

So, $f$ is not subjective

19.Prove that the Greatest Integer Function f: R → R given by f(x) = [x], is neither one-one nor onto, where [x] denotes the greatest integer less than or equal to x.

The $f x_{}^{n}$ $f : R \to R$ is given by $f (x) = [x]$

Let $x_{1} = 1.5$ and $x_{2} = 1.2 \in R$ Then,

$f (x_{1}) = f (1.5) = [1.5] = 1$

$f (x_{2}) = f (1.2) = [1.2] = 1$

So, $f (x_{1}) = f (x_{2})$ but $x_{1} \neq x_{2}$

i.e., $f (1.5) = f (1.2)$ but $1.5 \neq 1.2$

So, $f$ is not one-one

The range of $f (x)$ is a set of all integers, $Z$ which is not a co-domain of $R$

$∴ f$ is not onto

20. Show that the Modulus Function f : R → R, given by f(x) = |x| is neither one-one nor onto, where is |x| if x is positive or 0 and |-x| is -x if x is negative.

The $f x_{}^{n}$ $f : R \to R$ is given by $f (x) = | x |$

$\Rightarrow f (x) = (\begin{matrix} x_{}, i f & x \geq 0 \\ - x_{}, i f & x < 0 \end{matrix})$

For $x_{1} = - 1$ and $x_{2} = 1$

$f (x_{1}) = f (- 1) = | - 1 | = 1$

$f (x_{2}) = f (1) = | 1 | = 1$

So, $f (x_{1}) = f (x_{2})$ but $x_{1} \neq x_{2}$

i.e., $f$ is not one-one

For $x = - 1 \in R$

$f (x) = | x |$

i.e., $f (- 1) = | - 1 | = 1$

So, range of $f (x)$ is always a positive real number and is not equal to the co-domain $R$

i.e., $f$ is not onto

60. Show that the function f: R → R given by f(x) = x³ is injective.

f: R → R is given as f (x) = x³.

Suppose f (x) = f (y), where x, y ∈ R.

⇒ x³ = y³ … (1)

Now, we need to show that x = y.

Suppose x ≠ y, their cubes will also not be equal.

⇒ x³ ≠ y³

However, this will be a contradiction to (1).

∴ x = y

Hence, f is injective.

21. Show that the Signum Function f: R → R , given by $f (x) = {\begin{cases} 1 i f x > 0 \\ 0 i f x = 0 \\ - 1 i f x < 0 \end{cases}$ is neither one-one nor onto.

The $f x_{}^{n}$ $f : R ? R$ is given by $f (x) = (\begin{matrix} 1_{} & i f & x > 0 \\ 0_{} & i f & x = 0 \\ ? 1_{} & i f & x < 0 \end{matrix})$

For $x_{1} = 1, x_{2} = 2, ? R$

$f (x_{1}) = f (1) = 1$

$f (x_{2}) = f (2) = 1$ but $1 ? 2$

So, $f$ is not one-one

And the range of $f (x) = {1, 0, ? 1}$ hence it is not equal to the co-domain $R$

So, $f$ is not onto

Relation and Function Exercise 1.2 Solutions

17. Show that the function f: R* → R* defined by f(x) = 1/x is one-one and onto, where: R* is the set of all non-zero real numbers. Is the result true, if the domain: R* is replaced by N with the co-domain being same as: R*?

The $f x$ n is $f (x) = \frac{1}{x}$ , which is a $f : R_{*}$ $\to$ $R_{*}$ and $R_{*}$ is set of all non-zero real numbers

For, $x_{1}, x_{2} \in R_{*}, f (x_{1}) = f (x_{2})$

$\Rightarrow \frac{1}{x_{1}} = \frac{1}{x_{2}}$

$\Rightarrow x_{1} = x_{2}$ So, $f$ is one-one

For, $y \in R_{*},$ $x = \frac{1}{f (x)} = \frac{1}{y}$ such that

So, $f (x) = y$

So, every element in the co-domain has a pre-image in $f$

So, $f$ is onto

If $f : N \to R_{*}$ such that $f (x) = \frac{1}{x}$

For, $x_{1}, x_{2} \in N,$ $f (x_{1}) = f (x_{2})$

$\Rightarrow \frac{1}{x_{1}} = \frac{1}{x_{2}}$

$\Rightarrow x_{1} = x_{2}$ So, $f$ is one-one

For, $y \in R_{*}$ and $f (x) = y$ we have $x = \frac{1}{y} \notin N$

Eg., $3 \in R_{*}$ so $x = \frac{1}{3} \notin N$

So, $f$ is not onto

8. Show that the relation R in the set A = {1, 2, 3, 4, 5} given by R = {(a,b) : |a-b| is even} is an equivalence relation. Show that all the elements of {1, 3, 5} are related to each other and all the elements of {2, 4} are related to each other. But no element of {1, 3, 5} is related to any element of {2, 4}.

We have,

R= ${(a, b) ∴ | a - b |$ is even $}$ is a relation in set A= ${1, 2, 3, 4, 5}$

For all $a \in A$ , $| a - a | = 0$ is even.

So, $(a, a) \in R$ . Hence R is reflexive

For $a, b \in A$ and $(a, b) \in R$

$| a - b |$ is even

$| - b + a |$ is even $|$

$| - (b - a) |$ is even

$| b - a |$ is even

i.e., $(b, a) \in R$

Hence, R is symmetric.

For $a, b, c \in A$ and $(a, b) \in R$ and $(b, c) \in R$

We have $| a - b |$ is even

and $| b - c |$ is even

then, $| a - b | + | b - c |$ is even as even + even=even

$| a - b + b - c |$ is even

$| a - c |$ is even

$∴$ $(a, c) \in R$

So, R is transitive.

$∴$ R is an equivalence relation

All elements of [1,3,5] are odd positive numbers and its subset are odd and their difference given an even number. Hence, they are related to each other.

Similarly, all elements of [2,4] are even positive numbers and its subset are even and their difference gives an even number. Hence, they are related to each other.

However, elements of [1,3,5] are related to elements of [2,4] since the difference of the two subsets is never even.

3. Check whether the relation R defined in the set {1, 2, 3, 4, 5, 6} as

R = {(a, b): b = a + 1} is reflexive, symmetric or transitive.

We have,

R= ${(a, b) : b = a + 1}$ is a relation in set ${1, 2, 3, 4, 5, 6}$

So, R= ${(1, 2), (2, 3), (3, 4), (4, 5), (5, 6), (6, 7)}$

As, $(1, 1) \notin R$ , R is not reflexive

As, $(1, 2) \in R$ but $(2, 1) \notin R$ , R is not symmetric

And as $(1, 2)$ & $(2, 3) \in R$ but $(1, 3) \notin R$

Hence, R is not transitive.

61. Give examples of two functions f: N → Z and g: Z → Z such that g o f is injective but g is not injective.

(Hint: Consider f(x) = x and g(x) = |x| )

Define $f : N \to Z$ as $f (x)$ and $g : Z \to Z$ as $g (x) = | x |$

We first show that g is not injective.

It can be observed that:

$\begin{array}{l} g (- 1) = | - 1 | = 1 \\ g (1) = | 1 | = 1 \\ ∴ g (- 1) = g (1), b u t, - 1 \neq 1 \end{array}$

$∴ g$ is not injective.

Now, $g o f : N \to Z$ is defined as

$g o f (x) = y (f (x)) = y (x) = | x |$

Let $x, y \in N$ such that $g o f (x) - g o f (y)$

$\Rightarrow | x | = | y |$

Since $x, y \in N$ , both are positive.

$∴ | x | = | y | \Rightarrow x = y$

Hence, gof is injective

Relation and Function Exercise 1.3 Solutions

29. Let f: {1, 3, 4} → {1, 2, 5} and g: {1, 2, 5} → {1, 3} be given by f = {(1, 2), (3, 5), (4, 1)} and g = {(1, 3), (2, 3), (5, 1)}. Write down gof.

The functions f: {1, 3, 4} → {1, 2, 5} and g: {1, 2, 5} → {1, 3} are defined as

f = { (1, 2), (3, 5), (4, 1)} and g = { (1, 3), (2, 3), (5, 1)}.

gof (1) = g (f (1) = g (2) = 3 [f (1) = 2 and g (2) = 3]

gof (3) = g (f (3) = g (5) = 1 [f (3) = 5 and g (5) = 1]

gof (4) = g (f (4) = g (1) = 3 [f (4) = 1 and g (1) = 3]

$∴$ gof = { (1, 3), (3, 1), (4, 3)}

35. Consider f : R→ R given by f(x) = 4x + 3 Show that f is invertible. Find the inverse of f.

$f : R \to R$ is given by,

$\begin{array}{l} f (x) = 4 x + 3 \\ O n e - o n e : \\ L e t, f (x) = f (y) . \\ \Rightarrow 4 x + 3 = 4 y + 3 \\ \Rightarrow 4 x = 4 y \\ \Rightarrow x = y \end{array}$

$∴$ f is a one-one function.

Onto:

$\begin{array}{l} F o r, y \in R, l e t, y = 4 x + 3 . \\ \Rightarrow x = \frac{y - 3}{4} \in R \end{array}$

Therefore, for any $y \in R$ , there exists $x = \frac{y - 3}{4} \in R$ such that

$f (x) = f (\frac{y - 3}{4}) = 4 (\frac{y - 3}{4}) + 3 = y$

$∴$ f is onto.

Thus, f is one-one and onto and therefore, $f^{- 1}$ exists.

Let us define $g : R \to R$ by $g (x) = \frac{y - 3}{4}$

$\begin{array}{l} N o w, (g o f) (x) = g (f (x)) = g (4 x + 3) = \frac{(4 x + 3) - 3}{4} = x \\ (f o g) (y) = f (g (y)) = f (\frac{y - 3}{4}) = 4 (\frac{y - 3}{4}) + 3 = y - 3 + 3 = y \\ ∴ g o f = f o g = I_{R} \end{array}$

Hence, f is invertible and the inverse of f is given by

$f^{- 1} = g (y) = \frac{y - 3}{4}$

Relation and Function Exercise 1.1 Solutions

1. Determine whether each of the following relations are reflexive, symmetric and transitive:

(i) Relation R in the set A = {1, 2, 3…13, 14} defined as

R = {(x, y): 3x − y = 0}

(ii) Relation R in the set N of natural numbers defined as

R = {(x, y): y = x + 5 and x < 4}

(iii) Relation R in the set A = {1, 2, 3, 4, 5, 6} as

R = {(x, y): y is divisible by x}

(iv) Relation R in the set Z of all integers defined as

R = {(x, y): x − y is as integer}

(v) Relation R in the set A of human beings in a town at a particular time given by

(a) R = {(x, y): x and y work at the same place}

(b) R = {(x, y): x and y live in the same locality}

(c) R = {(x, y): x is exactly 7 cm taller than y}

(d) R = {(x, y): x is wife of y}

(e) R = {(x, y): x is father of y}

(i) We have, $R = {(x, y) : 3 x - y = 0}$ a relation in set A= ${1, 2, 3 . . . . . . . . . . 14}$

For $x \in A, y = 3 x$ or $y \neq x$ i.e.,

$(x, x)$ does not exist in R

$∴$ R is not reflexive.

For $(x, y) \in R, y = 3 x$

Then $(y, x) x \neq 3 y$

So $(y, x) \notin R$

$∴$ R is not symmetric

For $(x, y) \in R$ and $(y, z) \in R$ . We have

$y = 3 x$ and $z = 3 y$

Then $z = 3 (3 x) = 9 x$

i.e., $(x, z) \notin R$

$∴$ R is not Transitive

(ii) We have,

R= ${(x, y) : y = x + 5 & x < 4}$ is a relation in N

= ${(1, 1 + 5), (2, 2 + 5), (3, 3 + 5)}$

= ${(1, 6), (2, 7), (3, 8)}$

Clearly, R is not reflexive as $(x, x) \notin R$ and $x < 4 & x \in N$

Also, R is not symmetric as $(1, 6) \in R$ but $(6, 1) \notin R$

And for $(x, y) \in R (y, z) \notin R$ . Hence, R is not Transitive.

(iii) R= ${(x, y); y$ is divisible by x $}$ is a relation in set

A= ${1, 2, 3, 4, 5, 6}$

So, R= ${(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (5, 5), (6, 6)}$

Hence, R is reflexive because $(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6) \in R$ i.e., $(x, x) \in R$

R is not symmetric as $(1, 2) \in R$ but $(2, 1) \notin R$

And for $x, y, z \in A$ and $(x, y) \in R & (y, z) \in R$

$\frac{y}{z} = n$ and $\frac{z}{y} = m$ where $n & m \in N$

Then, $z = m y = m (n x) = m n . x$

$\frac{z}{x} = m . n, m, m n \in N$

Hence, $(x, z) \in R$

$∴$ R is transitive

(iv) R= ${(x, y) : x - y$ is an integer $}$ is a relation in set Z

For $x \in Z$

$x - x = 0$ is an integer

So, $(x, x) \in R$ i.e., R is reflexive

For $x, y \in Z$ and $(x, y) \in R$

$x - y$ is an integer

$- (y - x)$ is an integer

$(y - x)$ is an integer

So, $(y, x) \in R$ i.e., R is symmetric

For $x, y, z \in R$ and $(x, y) \in R & (y, z) \in R$ We have,

$x - y$ is an integer

$y - z$ is an integer

So, $(x - y) + (y - z)$ is also an integer

$x - z$ is an integer

So, $(x, z) \in R$ i.e., R is transitive.

(v) (a) R= ${(x, y) : x$ and $y$ work at same place $}$ in set A of human being.

For $x \in A$ we get

$x & x$ work at same place

$(x, x) \in R$ So, R is reflexive.

For $x, y \in A$ and $(x, y) \in R$ We get,

$x & y$ work at same place

$y & x$ work at same place

$(y, x) \in R$ . So, R is symmetric.

For $x, y, z \in A$ and $(x, y)$ and $(y, z) \in R$ . We have,

$x & y$ work at same place

$y & z$ work at same place

$x & z$ work at same place

i.e., $(x, z) \in R$ . So, R is Transitive.

(b) R= ${(x, y) : x & y$ live in same locality $}$

For $x \in A$ , we get,

$x & x$ live in same locality

$(x, x) \in R$ So, R is reflexive.

For $x, y \in A$ and $(x, y) \in R$ we get,

$x & y$ live in same locality

$y & x$ live in same locality

i.e., $(y, x) \in R$ . So, R is symmetric.

For $x, y, z \in A$ and $(x, y)$ & $(y, z) \in R$ . Then

$x, y$ live in same locality

$y, z$ live in same locality

$x, z$ live in same locality

So, $(x, z) \in R$ i.e., R is transitive.

(c) R= ${(x, y) : x$ is exactly 7 cm taller than y $}$

For $x \in A$ ,

Height $(x) \neq 7 +$ height of $(x)$

So, $(x, x) \notin R$ . i.e., R is not reflexive.

For, $x, y \in A$ and $(x, y) \in R$ we have,

Height $(x)$ $= 7 + h e i g h t (y)$

But $h e i g h t (y) \neq 7 + h e i g h t (x)$

So, $(y, x) \in R$ i.e., R is not symmetric.

For $x, y, z \in A$ and $(x, y) \in R$ and $(y, z) \in R$ we have,

Height $(x) = 7 + h e i g h t (y)$

And $h e i g h t (y) = 7 + h e i g h t (z)$

So, $h e i g h t (x) = 7 + 7 + h e i g h t (z) = 14 + h e i g h t (z)$

i.e., $(x, z) \notin R$

So, R is not transitive.

(d) R= ${(x, y) : x$ is wife of y $}$

For $x \in A,$

X is not wife of x.

So, $(x, x) \notin R$ i.e., R is not reflexive.

For $x, y \in A$ and $(x, y) \in R$ ,

X is wife of y but y is not wife of x

So, $(y, x) \notin R$ . i.e., R is not symmetric.

For $x, y, z \in A$ and $(x, y)$ and $(y, z) \in R$

X is wife of y

Y is wife of z

But y can never be husband & wife simultaneously

So, R is not transitive.

(e) R= ${(x, y) : x$ is father of y $}$

For $x \in A$ ,

X is not a father of x

So, $(x, x) \notin R$ i.e., R is not reflexive.

For $x, y \in A$ and $(x, y) \in R$

X is father of y

Y is father of z

But x is not father of z

So, $(x, z) \notin R$ i.e., R is not transitive.

63. Given a non empty set X, consider P(X) which is the set of all subsets of X.

Define the relation R in P(X) as follows: For subsets A, B in P(X), ARB if and only if A ⊂ B. Is R an equivalence relation on P(X)? Justify you answer:

Since every set is a subset of itself, ARA for all A ∈ P (X).

∴R is reflexive.

Let ARB ⇒ A ⊂ B.

This cannot be implied to B ⊂ A.

For instance, if A = {1, 2} and B = {1, 2, 3}, then it cannot be implied that B is related to A.

∴ R is not symmetric.

Further, if ARB and BRC, then A ⊂ B and B ⊂ C.

⇒ A ⊂ C

⇒ ARC

∴ R is transitive.

Hence, R is not an equivalence relation since it is not symmetric.

71. Let A = {1, 2, 3}. Then number of relations containing (1, 2) and (1, 3) which are reflexive and symmetric but not transitive is:

(A) 1

(B) 2

(C) 3

(D) 4

It is clear that 1 is reflexive and symmetric but not transitive.

Therefore, option (A) is correct.

42. Let $f : R - {- \frac{4}{3}} \to R$ be a function defined as $f (x) = \frac{4 x}{3 x + 4}$ . The inverse of f is map g Range $f \to R - {- \frac{4}{3}}$

$g (y) = \frac{3 y}{3 - 4 y}$

$g (y) = \frac{4 y}{4 - 3 y}$

$g (y) = \frac{4 y}{3 - 4 y}$

$g (y) = \frac{3 y}{4 - 3 y}$

It is given that $f : R - {- \frac{4}{3}} \to R$ is defined as $f (x) = \frac{4 x}{3 x - 4}$

Let y be an arbitrary element of Range f.

Then, there exists $x \in R - {- \frac{4}{3}}$ such that $y = f (x)$

$\Rightarrow y = \frac{4 x}{3 x + 4}$

$\Rightarrow 3 x y + 4 y = 4 x$ let us define g: Range $f \to R - {- \frac{4}{3}} a s, g (y) = \frac{4 y}{4 - 3 y}$

$\begin{array}{l} \Rightarrow x (4 - 3 y) = 4 y \\ N o w, (g o f) (x) = g (f (x)) = g (\frac{4 x}{3 x + 4}) \\ \Rightarrow x = \frac{4 y}{4 - 3 y} \\ = \frac{4 (4 \frac{x}{3 x + 4})}{4 - 3 (\frac{4 x}{3 x + 4})} = \frac{16 x}{12 x + 16 - 12 x} = \frac{16 x}{16} = x \\ A n d, (f o g) (y) = f (g (y)) = f (\frac{4 y}{4 - 3 y}) \\ = \frac{4 (\frac{4 y}{4 - 3 y})}{3 (\frac{4 y}{4 - 3 y}) + 4} = \frac{16 y}{12 y + 16 - 12 y} = \frac{16 y}{16} = y \\ ∴ g o f = I_{R - (- \frac{4}{3})} a n d, f o g = I_" R a n g e, f " \end{array}$

Thus, g is the inverse of f i.e., $f^{- 1} = g .$

Hence, the inverse of f is the map g: Range $f \to R - {- \frac{4}{3}}$ which is given by

$g (y) = \frac{4 y}{4 - 3 y}$

The correct answer is B.

33. State with reason whether following functions have inverse

(i) f: {1, 2, 3, 4} → {10} with f = {(1, 10), (2, 10), (3, 10), (4, 10)}

(ii) g: {5, 6, 7, 8} → {1, 2, 3, 4} with g = {(5, 4), (6, 3), (7, 4), (8, 2)}

(iii) h: {2, 3, 4, 5} → {7, 9, 11, 13} with h = {(2, 7), (3, 9), (4, 11), (5, 13)}

(i) f: {1, 2, 3, 4} → {10} defined as:

f = { (1, 10), (2, 10), (3, 10), (4, 10)}

From the given definition of f, we can see that f is a many one function as: f (1) = f (2) = f (3) = f (4) = 10

∴f is not one-one.

Hence, function f does not have an inverse.

(ii) g: {5, 6, 7, 8} → {1, 2, 3, 4} defined as:

g = { (5, 4), (6, 3), (7, 4), (8, 2)}

From the given definition of g, it is seen that g is a many one function as: g (5) = g (7) = 4.

∴g is not one-one,

Hence, function g does not have an inverse.

(iii) h: {2, 3, 4, 5} → {7, 9, 11, 13} defined as:

h = { (2, 7), (3, 9), (4, 11), (5, 13)}

It is seen that all distinct elements of the set {2, 3, 4, 5} have distinct images under h.

∴Function h is one-one.

Also, h is onto since for every element y of the set {7, 9, 11, 13}, there exists an element x in the set {2, 3, 4, 5} such that h (x) = y.

Thus, h is a one-one and onto function. Hence, h has an inverse.

54. State whether the following statements are true or false. Justify.

(i) For an arbitrary binary operation * on a set N, a * a = a ∀ a * N.

(ii) If * is a commutative binary operation on N, then a * (b * c) = (c * b) * a

(i) Define an operation * on N as:

a * b = a + b a, b ∈ N

Then, in particular, for b = a = 3, we have:

3 * 3 = 3 + 3 = 6 ≠ 3

Therefore, statement (i) is false.

(ii) R.H.S. = (c * b) * a

= (b * c) * a [* is commutative]

= a * (b * c) [Again, as * is commutative]

= L.H.S.

∴ a * (b * c) = (c * b) * a

Therefore, statement (ii) is true.

12. Show that the relation R defined in the set A of all triangles as R = {(T₁, T₂): T₁ is similar to T₂}, is equivalence relation. Consider three right angle triangles T₁ with sides 3, 4, 5, T₂ with sides 5, 12, 13 and T₃ with sides 6, 8, 10. Which triangles among T₁, T₂ and T₃ are related?

The given relation to set A of all triangles is defined as

R= ${(T_{1}, T_{2}) : T_{1}$ is similar to $T_{2}}$

For $T_{1} \in A$ ,

$T_{1}$ is always similar to $T_{1}$

So, $(T_{1}, T_{1}) \in R$ . Hence R is reflexive.

For $T_{1,} T_{2} \in A$ and $(T_{1}, T_{2}) \in R$ we have

$T_{1} \sim T_{2} (s i m i l a r)$

$T_{2} \sim T_{1}$ i.e., $(T_{2}, T_{1}) \in R$

so, R is symmetric.

for, $T_{1}, T_{2}, T_{3} \in A$ and $(T_{1}, T_{2}) \in R$ and $(T_{2}, T_{3}) \in R$

$T_{1} \sim T_{2}$ and $T_{2} \sim T_{3}$

i.e., $T_{1} \sim T_{3}$ $\to (T_{1}, T_{3}) \in R$

so, R is transitive

$∴$ R is an equivalence relation.

Given, sides of $T_{1}$ are 3,4,5

Sides of $T_{2}$ are 5,12,13

Sides of $T_{3}$ are 6,8,10

As $\frac{3}{5} \neq \frac{4}{12} \neq \frac{5}{13}$ we conclude that $T_{1}$ is not similar to $T_{2}$

As $\frac{5}{6} \neq \frac{12}{8} \neq \frac{13}{10}$ we conclude that $T_{2}$ is not similar to $T_{3}$

But as $\frac{3}{6} = \frac{4}{8} = \frac{5}{10} = \frac{1}{2}$ we conclude that $T_{1} \sim T_{3}$

Hence, $T_{1}$ is related to $T_{3}$

70. Let A = {–1, 0, 1, 2}, B = {–4, –2, 0, 2} and f; g: A→B be the functions defined by f(x) = x² − x, x ∈ A and g(x) = 2x - 1/2 - 1. x∈ A. Are f and g equal? Justify your answer.

(Hint: One may note that two functions f: A → B and g: A → B such that f(a) = g(a) & mn For E; a ∈A, are called equal functions).

It is given that A = {–1, 0, 1, 2}, B = {–4, –2, 0, 2}

Also, it is given that $f, g : A \to B$ are defined by $f (x) = x^{2} - x, x \in A$ and $g (x) = 2 x - \frac{1}{2} - 1, x \in A$ .

It is observed that:

$\begin{array}{l} f (- 1) = (1^{2}) - (- 1) = 1 + 1 = 2 \\ g (- 1) = 2 (- 1) - \frac{1}{2} - 1 = 2 (\frac{3}{2}) - 1 = 3 - 1 = 2 \\ \Rightarrow f (- 1) = g (- 1) \\ f (0) = {(0)}^{\land} 2 - 0 = 0 \\ g (0) = 2 (0) - \frac{1}{2} - 1 = 2 (\frac{1}{2}) - 1 = 1 - 1 = 0 \\ \Rightarrow f (0) = g (0) \\ f (1) = {(1)}^{\land} 2 - 1 = 1 - 1 = 0 \\ g (1) = 2 a - \frac{1}{2} - 1 = 2 (\frac{1}{2}) - 1 = 1 - 1 = 0 \\ \Rightarrow f (1) = g (1) \\ f (2) = {(2)}^{\land} 2 - 2 = 4 - 2 = 2 \\ g (2) = 2 (2) - \frac{1}{2} - 1 = 2 (\frac{3}{2}) - 1 = 3 - 1 = 2 \\ \Rightarrow f (2) = g (2) \\ ∴ f (a) = g (a) \forall a \in A \end{array}$

Hence, the functions f and g are equal.

59. Show that function f: R → {x ∈ R: −1 < x < 1} defined by f(x) = x/1+|x| x ∈R is one-one and onto function.

It is given that $f : R \to {x \in R : - 1 < x < 1}$ is defined as $f (x) = \frac{x}{1 + | x |}, x \in R .$

Suppose $f (x) = f (y)$ , where $x, y \in R .$

$\Rightarrow \frac{x}{1 + x} = \frac{y}{1 - y} \Rightarrow 2 x y = x - y$

Since x is positive and y is negative:

$x > y \Rightarrow x - y > 0$

But, 2xy is negative.

Then, $2 x y \neq x - y$ .

Thus, the case of x being positive and y being negative can be ruled out.

Under a similar argument, x being negative and y being positive can also be ruled out

$∴$ x and y have to be either positive or negative.

When x and y are both positive, we have:

$f (x) = f (y) \Rightarrow \frac{x}{1 + x} = \frac{y}{1 + y} \Rightarrow x + x y = y + x y \Rightarrow x = y$

When x and y are both negative, we have:

$f (x) = f (y) \Rightarrow \frac{x}{1 - x} = \frac{y}{1 - y} \Rightarrow x - x y = y - y x \Rightarrow x = y$

$∴ f$ is one-one.

Now, let $y \in R$ such that $- 1 < y < 1$ .

If x is negative, then there exists $x = \frac{y}{1 + y} \in R$ such that

$f (x) = f (\frac{y}{1 + y}) = \frac{(\frac{y}{1 + y})}{1 + \frac{y}{1 + y}} = \frac{\frac{y}{1 + y}}{1 + \frac{- y}{1 + y}} = \frac{y}{1 + y - y} = y$

If x is positive, then there exists $x = \frac{y}{1 - y} \in R$ such that

$f (x) = f (\frac{y}{1 - y}) = \frac{(\frac{y}{1 - y})}{1 + (\frac{y}{1 - y})} = \frac{\frac{y}{1 - y}}{1 + \frac{y}{1 - y}} = \frac{y}{1 - y + y} = y$

$∴ f$ is onto.

Hence, f is one-one and onto.

23. In each of the following cases, state whether the function is one-one, onto or bijective. Justify your answer.

(i) f: R → R defined by f(x) = 3 − 4x

(ii) f: R → R defined by f(x) = 1 + x²

(i) $f : R \to R$ defined as $f (x) = 3 - 4 x$

For $x_{1}, x_{2} \in R$ such that $f (x_{1}) = f (x_{2})$

$\begin{array}{l} \Rightarrow 3 - 4 x_{1} = 3 - 4 x_{2} \\ \Rightarrow 4 x_{1} = 4 x_{2} \\ \Rightarrow x_{1} = x_{2} \end{array}$

So, $f$ is one-one

For $y \in R$ , there exist

$f (\frac{. 3 - y}{4}) = 3 - 4 (\frac{3 - y}{4}) = 3 - 3 + y = y$

Hence, $f$ is onto

$∴ f$ is bijective

(ii) Given, $f : R \to R$ defined as $f (x) = 1 + x_{}^{2}$

For $x_{1}, x_{2} \in R$ such that $f (x_{1}) = f (x_{2})$

$\begin{array}{l} \Rightarrow 1 + x_{1}^{2} = 1 + x_{2}^{2} \\ \Rightarrow x_{1}^{2} = x_{2}^{2} \\ \Rightarrow x_{1}^{} = \pm x_{2}^{} \end{array}$

$\Rightarrow x_{1}^{} = x_{2}^{}$ or $x_{1}^{} = - x_{2}^{}$

$∴ f$ is not one-one

The range of $f (x)$ is always a positive real number which is not equal to co-domain $R$

So, $f$ is not onto

72. Let A = {1, 2, 3}. Then number of equivalence relations containing (1, 2) is:

(A) 1

(B) 2

(C) 3

(D) 4

2, Therefore, option (B) is correct.

10. Given an example of a relation. Which is

(i) Symmetric but neither reflexive nor transitive.

(ii) Transitive but neither reflexive nor symmetric.

(iii) Reflexive and symmetric but not transitive.

(iv) Reflexive and transitive but not symmetric.

(v) Symmetric and transitive but not reflexive.

Let A= ${a, b, c}$

(i) R= ${(a, b), (b, a)}$ is a relation in set A

So, $(a, b) \in R$ and $(b, a) \in R \to$ Symmetric

$(a, a) \notin R \to$ not reflexive

$(a, b) \in R, (b, a) \in R$ but $(a, a) \notin R$ $\to$ not transitive

(ii) R= ${(a, b), (b, c), (a, c)}$ is a relation in set A

So, $(a, a) \notin R \to$ not reflexive

$(a, b) \in R$ but $(b, a) \notin R \to$ not symmetric

$(a, b) \in R & (b, c) \in R$ and also $(a, c) \in R \to$ transitive

(iii) R= ${(a, a), (b, b), (c, c), (a, b), (b, a), (a, c), (c, a)}$

So, $(a, a), (b, b), (c, c) \in R \to$ Reflexive

$(a, b) \in R \to (b, a) \in R \to$ Symmetric

$(a, c) \in R \to (c, a) \in R$

$(b, a) \in R$ and $(a, c) \in R$

But $(b, c) \notin R \to$ not transitive

(iv) R= ${(a, a), (b, b), (c, c), (a, b), (b, c), (a, c)}$ is s relation in set A

So, $(a, a), (b, b), (c, c) \in R \to$ reflexive

$(a, b) & (b, c) \in R$ so, $(a, c) \in R \to$ transitive

$(a, b) \in R$ but $(b, a) \notin R \to$ not symmetric

(v) R= ${(a, a), (a, b), (b, a)}$

So, $(b, b) \notin R \to$ not reflexive

$(a, b) \in R$ and $(b, a) \in R \to$ symmetric

And $(a, b) \in R & (b, a) \in R$

and also $(a, a) \in R \to$ transitive

6. Show that the relation R in the set {1, 2, 3} given by R = {(1, 2), (2, 1)} is symmetric but neither reflexive nor transitive.

We have,

R= ${(1, 2), (2, 1)}$ is a relation in set ${1, 2, 3}$

Then, as $(1, 1) \notin R$ and $(2, 2) \notin R$

So, R is not reflective

As $(1, 2) \in R$ and $(2, 1) \in R$

So, R is symmetric

And as $(1, 2) \in R, (2, 1) \in R$ but $(1, 1) \notin R$

So, R is not transitive.

MISCELLANEOUS

56. Let f: R → R be defined as f(x) = 10x + 7. Find the function g: R → R such that g o f = f o g = 1R.

It is given that $f : R \to R$ is defined as $f (x) = 10 x + 7 .$

One-one:

$\begin{array}{l} L e t, f (x) = f (y), w h e r e, x, y \in R \\ \Rightarrow 10 x + 7 = 10 y + 7 \\ \Rightarrow x = y \end{array}$

$∴ f$ is a one-one function.

Onto:

$\begin{array}{l} F o r, y \in R, l e t, y = 10 x + 7 \\ \Rightarrow x = \frac{y - 7}{10} \in R \end{array}$

Therefore, for any $y \in R$ ,there exists $x = \frac{y - 7}{10} \in R$

Such that

$f (x) = f (\frac{y - 7}{10}) = 10 (\frac{y - 7}{10}) + 7 = y - 7 + 7 = y$

$∴ f$ is onto.

Therefore, f is one-one and onto.

Thus, f is an invertible function.

Let us define $g : R \to R$ as $g (y) = \frac{y - 7}{10}$

Now, we have

$\begin{array}{l} g o f (x) = g (f (x)) = g (10 x + 7) = \frac{(10 x + 7) - 7}{10} = 10 \frac{x}{10} = 10 \\ A n d \\ f o g (y) = f (g (y)) = f (\frac{y - 7}{10}) = 10 (\frac{y - 7}{10}) + 7 = y - 7 + 7 = y \end{array}$

Hence, the required function $g : R \to R$ is defined as $g (y) = \frac{y - 7}{10}$

28.Let f: R → R be defined as f(x) = 3x. Choose the correct answer.

(A) F is one-one onto

(B) F is many-one onto

(C) F is one-one but not onto

(D) F is neither one-one nor onto

Given, $f : R \to R$ defined as $f (x) = 3 x$

For $x_{1}, x_{2} \in R$ such that $f (x_{1}) = f (x_{2})$

$\Rightarrow 3 x_{1}^{} = 3 x_{2}^{}$

$\Rightarrow x_{1}^{} = x_{2}^{}$

So, $f$ is one-one

And for $y \in R$ , there exist $\frac{y}{3} \in R$ such that

$f (\frac{y}{3}) = \frac{3 \times y}{3} = y$

$∴ f$ is onto

Hence, option (A) is correct.

16. Let R be the relation in the set N given by R = {(a, b): a = b − 2, b > 6}. Choose the correct answer.

(A) (2, 4) ∈ R (B) (3, 8) ∈R (C) (6, 8) ∈R (D) (8, 7) ∈ R

The given relation in set N defined by

$R = {(a, b) : a = b - 2, b > 6}$

For (2,4), 4>6 is not true

For (3,8), 8>6 but 3= 8-2 ⇒3=6 is not true

For (6,8), 8>6 and 6= 8-2 ⇒6=6 is true

And for (8,7), 7>6 but 8= 7-2 ⇒8=5 is not true

Hence, option (C) is correct

30. Let f, g and h be functions from R to R. Show that:

(f + g) oh = foh + goh

(f.g) oh = (foh). (goh)

To prove:

$\begin{array}{l} (f + g) o h = f o h + g o h \\ c o n s i d e r : \\ ((f + g) o h) (x) \\ = (f + g) (h (x)) \\ = f (h (x)) + g (h (x)) \\ = (f o h) (x) + (g o h) (x) \\ = {(f o h) + (g o h)} (x) \\ ∴ ((f + g) o h) (x) = {(f o h) + (g o h)} (x), \forall x \in R \\ H e n c e, (f + g) o h = f o h + g o h \end{array}$

To prove

$\begin{array}{l} (f . g) o h = (f o h) . (g o h) \\ C o n s i d e r \\ ((f . g) o h) (x) \\ = (f . g) (h (x)) \\ = f (h (x)) . g (h (x)) \\ = (f o h) (x) . (g o h) (x) \\ = {(f o h) . (g o h)} (x) \\ ∴ ((f . g) o h) (x) = {(f o h) . (g o h)} (x), \forall x \in R \\ H e n c e, (f . g) o h = (f o h) . (g o h) \end{array}$

Exercise-1.4

43. Determine whether or not each of the definition of given below gives a binary operation. In the event that * is not a binary operation, give justification for this.

(i) On Z⁺ , define * by a * b = a − b

(ii) On Z⁺, define * by a * b = ab

(iii) On R, define * by a * b = ab²

(iv) On Z⁺, define * by a * b = |a − b|

(v) On Z⁺, define * by a * b = a

(i) On Z⁺, * is defined by a * b = a − b.

It is not a binary operation as the image of (1, 2) under * is 1 * 2 = 1 − 2= −1 ∉ Z⁺.

(ii) On Z⁺, * is defined by a * b = ab.

It is seen that for each a, b ∈ Z⁺, there is a unique element ab in Z⁺.

This means that * carries each pair (a, b) to a unique element a * b = ab in Z⁺.

Therefore, * is a binary operation.

(iii) On R, * is defined by a * b = ab².

It is seen that for each a, b ∈ R, there is a unique element ab² in R.

This means that * carries each pair (a, b) to a unique element a * b = ab² in R.

Therefore, * is a binary operation.

(iv) On Z⁺, * is defined by a * b = |a − b|.

It is seen that for each a, b ∈ Z+, there is a unique element |a − b| in Z⁺.

This means that * carries each pair (a, b) to a unique element a * b = |a − b| in Z⁺.

Therefore, * is a binary operation.

(v) On Z⁺, * is defined by a * b = a.

* carries each pair (a, b) to a unique element a * b = a in Z⁺.

Therefore, * is a binary operation.

44. For each binary operation * defined below, determine whether * is commutative or associative:

(i) On Z, define a * b = a − b

(ii) On Q, define a * b = ab + 1

(iii) On Q, define a * b =ab/2

(iv) On Z⁺, define a * b = 2^ab

(v) On Z⁺, define a * b = a^b

(vi) On R − {−1}, define a.b = a/b+1

(i) On Z, * is defined by a * b = a − b.

It can be observed that 1 * 2 = 1 − 2 = 1 and 2 * 1 = 2 − 1 = 1.

∴1 * 2 ≠ 2 * 1; where 1, 2 ∈ Z

Hence, the operation * is not commutative.

Also we have:

(1 * 2) * 3 = (1 − 2) * 3 = −1 * 3 = −1 − 3 = −4

1 * (2 * 3) = 1 * (2 − 3) = 1 * −1 = 1 − (−1) = 2

∴(1 * 2) * 3 ≠ 1 * (2 * 3) ; where 1, 2, 3 ∈ Z

Hence, the operation * is not associative.

(ii) On Q, * is defined by a * b = ab + 1.

It is known that:

ab = ba & mn For E; a, b ∈ Q

⇒ ab + 1 = ba + 1 & mn For E; a, b ∈ Q

⇒ a * b = a * b &mn For E; a, b ∈ Q

Therefore, the operation * is commutative.

It can be observed that:

(1 * 2) * 3 = (1 × 2 + 1) * 3 = 3 * 3 = 3 × 3 + 1 = 10

1 * (2 * 3) = 1 * (2 × 3 + 1) = 1 * 7 = 1 × 7 + 1 = 8

∴(1 * 2) * 3 ≠ 1 * (2 * 3) ; where 1, 2, 3 ∈ Q

Therefore, the operation * is not associative.

(iii) On Q, * is defined by a * b = ab/2

It is known that:

ab = ba &mnForE; a, b ∈ Q

⇒ab/2 = ba/2 &mnForE; a, b ∈ Q

⇒ a * b = b * a &mnForE; a, b ∈ Q

Therefore, the operation * is commutative.

For all a, b, c ∈ Q, we have:

$\begin{array}{l} (a * b) * c = (\frac{a b}{2}) * c = \frac{(\frac{a b}{2}) c}{2} = \frac{a b c}{4} \\ a * (b * c) = a * (\frac{b c}{2}) = \frac{a (\frac{b c}{2})}{2} = \frac{a b c}{4} \\ ∴ (a * b) * c = a * (b * c) \end{array}$

Therefore, the operation * is associative.

(iv) On Z⁺, * is defined by a * b = 2^ab.

It is known that:

ab = ba &mnForE; a, b ∈ Z⁺

⇒ 2^ab = 2^ba &mnForE; a, b ∈ Z⁺

⇒ a * b = b * a &mnForE; a, b ∈ Z⁺

Therefore, the operation * is commutative.

It can be observed that:

$\begin{array}{l} (1 * 2) * 3 = 2^{(1 \times 2)} * 3 = 4 * 3 = 2^{4 \times 3} = 2^{12} \\ 1 * (2 * 3) = 1 * 2^{2 \times 3} = 1 * 2^{6} = 1 * 64 = 2^{64} \end{array}$

∴(1 * 2) * 3 ≠ 1 * (2 * 3) ; where 1, 2, 3 ∈ Z+

Therefore, the operation * is not associative.

(v) On Z⁺, * is defined by a * b = a^b.

It can be observed that:

1 x2 = 1²=1 and 2x 1 =2¹ = 2

∴ 1 * 2 ≠ 2 * 1 ; where 1, 2 ∈ Z⁺

Therefore, the operation * is not commutative.

It can also be observed that:

$\begin{array}{l} (2 * 3) * 4 = 2^{3} * 4 = 8 * 4 = 8^{4} = {(2^{3})}^{4} = 2^{12} \\ 2 * (3 * 4) = 2 * 3^{4} = 2 * 81 = 2^{81} \end{array}$

∴(2 * 3) * 4 ≠ 2 * (3 * 4) ; where 2, 3, 4 ∈ Z+

Therefore, the operation * is not associative.

(vi) On R, * − {−1} is defined by a.b = a/b+1

It can be observed that 1 x 2 = 1/2+1 = 1/2 and 2 x 1 = 2/1+1 = 2/2

∴1 * 2 ≠ 2 * 1 ; where 1, 2 ∈ R − {−1}

Therefore, the operation * is not commutative.

It can also be observed that:

$\begin{array}{l} (1 * 2) * 3 = \frac{1}{3} * 3 = \frac{\frac{1}{3}}{3 + 1} = \frac{1}{12} \\ 1 * (2 * 3) = 1 * \frac{2}{3 + 1} = 1 * \frac{2}{4} = 1 * \frac{1}{2} = \frac{1}{\frac{1}{2} + 1} = \frac{1}{\frac{3}{2}} = \frac{2}{3} \end{array}$

∴ (1 * 2) * 3 ≠ 1 * (2 * 3) ; where 1, 2, 3 ∈ R − {−1}

Therefore, the operation * is not associative.

46. Consider a binary operation * on the set {1, 2, 3, 4, 5} given by the following multiplication table.

(i) Compute (2 * 3) * 4 and 2 * (3 * 4)

(ii) Is * commutative?

(iii) Compute (2 * 3) * (4 * 5).

(Hint: use the following table)

*	1	2	3	4	5
1	1	1	1	1	1
2	1	2	1	2	1
3	1	1	3	1	1
4	1	2	1	4	1
5	1	1	1	1	5

(i) (2 * 3) * 4 = 1 * 4 = 1

2 * (3 * 4) = 2 * 1 = 1

(ii) For every a, b ∈ {1, 2, 3, 4, 5}, we have a * b = b * a. Therefore, the operation * is commutative.

(iii) (2 * 3) = 1 and (4 * 5) = 1

∴ (2 * 3) * (4 * 5) = 1 * 1 = 1

51. Let * be a binary operation on the set Q of rational numbers as follows:

(i) a * b = a − b

(ii) a * b = a² + b²

(iii) a * b = a + ab

(iv) a * b = (a − b)²

(v) a * b = ab/4 (vi) a * b = ab²

Find which of the binary operations are commutative and which are associative.

(i) On Q the operation* is defined as a*b=a-b.

It can be observed that:

$\begin{array}{l} \frac{1}{2} . \frac{1}{3} = \frac{1}{2} - \frac{1}{3} = \frac{3 - 2}{6} = \frac{1}{6} " a n d " \frac{1}{3} . \frac{1}{2} = \frac{1}{3} - \frac{1}{2} = \frac{2 - 3}{6} = \frac{- 1}{6} \\ ∴ \frac{1}{2} . \frac{1}{3} \neq \frac{1}{3} . \frac{1}{2} w h e r e, \frac{1}{2}, \frac{1}{3} \in Q \end{array}$

Thus, the operation* is not commutative.

It can also be observed that:

$\begin{array}{l} (\frac{1}{2} . \frac{1}{3}) . \frac{1}{4} = (\frac{1}{2} - \frac{1}{3}) . \frac{1}{4} = \frac{1}{6} . \frac{1}{4} = \frac{1}{6} - \frac{1}{4} = \frac{2 - 3}{12} = \frac{- 1}{12} \\ \frac{1}{2} . (\frac{1}{3} . \frac{1}{4}) = \frac{1}{2} . (\frac{1}{3} - \frac{1}{4}) = \frac{1}{2} . \frac{1}{12} = \frac{1}{2} - \frac{1}{12} = \frac{6 - 1}{12} = \frac{5}{12} \\ ∴ (\frac{1}{2} . \frac{1}{3}) . \frac{1}{4} \neq \frac{1}{2} . (\frac{1}{3} . \frac{1}{4}) w h e r e, \frac{1}{2}, \frac{1}{3}, \frac{1}{4} \in Q \end{array}$

Thus, the operation* is not associative.

(ii) On Q the operation* is defined as a*b=a²+b.

For $a, b \in Q$ , we have:

$\begin{array}{l} a . b = a^{2} + b^{2} = b^{2} + a^{2} = b . a \\ ∴ a * b = b * a \end{array}$

Thus, the operation* is commutative.

It can be observed that:

$\begin{array}{l} (1 * 2) * 3 = (12 + 22) * 3 = (1 + 4) * 3 = 5 * 3 = 52 + 32 = 25 + 9 = 34 \\ 1 * (2 * 3) = 1 * (22 + 32) = 1 * (4 + 9) = 1 * 13 = 12 + 132 = 1 + 169 = 170 \\ ∴ (1 * 2) * 3 \neq 1 * (2 * 3), w h e r e, 1, 2, 3 \in Q \end{array}$

Thus, the operation* is not commutative.

(iii) On Q the operation* is defined as a*b=a+ab.

It can be observed that:

$\begin{array}{l} 1.2 = 1 + 1 \times 2 = 1 + 2 = 3 \\ 2.1 = 2 + 2 \times 1 = 2 + 2 = 4 \\ ∴ 1.2 \neq 2.1, w h e r e, 1, 2 \in Q \end{array}$

Thus, the operation* is not commutative.

It can also be observed that:

$\begin{array}{l} (1.2) . 3 = (1 + 1 \times 2) . 3 = 3.3 = 3 + 3 \times 3 = 3 + 9 = 12 \\ 1 . (2.3) = 1 . (2 + 2 \times 3) = 1 + 1 \times 8 = 9 \\ ∴ (1.2) . 3 \neq 1 . (2.3), w h e r e, 1, 2, 3 \in Q \end{array}$

Thus, the operation* is not associative.

(iv) On Q the operation* is defined as a*b=(a-b)²

For $a, b \in Q$ , we have:

$\begin{array}{l} a * b = {(a - b)}^{2} \\ b * a = {(b - a)}^{2} = {[- (a - b)]}^{2} = {(a - b)}^{2} \\ ∴ a * b = b * a \end{array}$

Thus, the operation* is commutative.

It can be observed that:

$\begin{array}{l} (1.2) . 3 = {(1.2)}^{2} . 3 = {(- 1)}^{2} . 3 = 1.3 = {(1.3)}^{2} = {(- 2)}^{2} = 4 \\ 1 . (2.3) = 1 . {(2.3)}^{2} = 1 . {(- 1)}^{2} = 1.1 = {(1.1)}^{2} = 0 \\ ∴ (1.2) . 3 \neq 1 . (2.3), w h e r e, 1, 2, 3 \in Q \end{array}$

Thus, the operation* is not associative.

(v) On Q the operation* is defined as a.b=ab/4

For $a, b \in Q$ , we have:

$\begin{array}{l} a . b = \frac{a b}{4} = b \frac{a}{4} = b . a \\ ∴ a * b = b * a \end{array}$

Thus, the operation* is commutative.

For $a, b, c \in Q$ , we have:

$\begin{array}{l} (a . b) . c = \frac{a b}{4} . c = \frac{\frac{a b}{4} . c}{4} = \frac{a b c}{16} \\ a . (b . c) = a . b \frac{c}{4} = \frac{a . \frac{b c}{4}}{4} = \frac{a b c}{16} \\ = ∴ (a * b) * c \neq a * (b * c) \end{array}$

Thus, the operation* is associative.

(vi) On Q the operation* is defined as a*b=ab²

It can be observed that:

$\begin{array}{l} \frac{1}{2} . \frac{1}{3} = \frac{1}{2} . {(\frac{1}{3})}^{2} = \frac{1}{2} . \frac{1}{9} = \frac{1}{18} \\ \frac{1}{3} . \frac{1}{2} = \frac{1}{3} . {(\frac{1}{2})}^{2} = \frac{1}{3} . \frac{1}{4} = \frac{1}{12} \\ ∴ \frac{1}{2} . \frac{1}{3} \neq \frac{1}{3} . \frac{1}{2}, w h e r e, \frac{1}{2}, \frac{1}{3} \in Q \end{array}$

Thus, the operation* is not commutative.

It can be observed that:

$\begin{array}{l} (\frac{1}{2} . \frac{1}{3}) . \frac{1}{4} = [\frac{1}{2} . {(\frac{1}{3})}^{2}] . \frac{1}{4} = \frac{1}{18} . \frac{1}{4} = \frac{1}{18} . {(\frac{1}{4})}^{2} = \frac{1}{18 \times 16} \\ \frac{1}{2} . (\frac{1}{3} . \frac{1}{4}) = \frac{1}{2} . [\frac{1}{3} . {(\frac{1}{4})}^{2}] = \frac{1}{2} . \frac{1}{48} = \frac{1}{2} . {(\frac{1}{48})}^{2} = \frac{1}{2 \times {(48)}^{2}} \\ ∴ (\frac{1}{2} . \frac{1}{3}) . \frac{1}{4} \neq \frac{1}{2} . (\frac{1}{3} . \frac{1}{4}), w h e r e, \frac{1}{2}, \frac{1}{3}, 1.4 \in Q \end{array}$

Thus, the operation* is not associative.

Hence, the operations defined (ii), (iv), (v) are commutative and the operation defined in (v) is associative.

58. If f: R → R is defined by f(x) = x² − 3x + 2, find f(f(x)).

It is given that $f : R \to R$ is defined as $f (x) = x^{2} - 3 x + 2 .$

$\begin{array}{l} f (f (x)) = f (x^{2} - 3 x + 2) \\ = {(x^{2} + 3 x + 2)}^{2} - 3 (x^{2} - 3 x + 2) + 2 \\ = x^{4} + 9 x^{2} + 4 - 6 x^{2} - 12 x + 4 x^{2} - 3 x^{2} + 9 x - 6 + 2 \\ = x^{4} - 6 x^{2} + 10 x^{2} - 3 x \end{array}$

32. If $f (x) = \frac{4 x + 3}{6 x - 4}, x \neq \frac{2}{3}$ show that( fof) (x) = x for all x ≠ 2/3 What is the inverse of f

It is given that $f (x) = \frac{4 x + 3}{6 x - 4}, x \neq \frac{2}{3}$

$\begin{array}{l} (f o f) (x) = f (f (x)) = f (\frac{4 x + 3}{6 x - 4}) \\ = \frac{4 (\frac{4 x + 3}{6 x - 4}) + 3}{6 (\frac{4 x + 3}{6 x - 4}) - 4} = \frac{16 x + 12 + 18 x - 12}{24 x + 18 - 24 x + 16} = \frac{34 x}{34} = x \end{array}$

Therefore $f o f (x) = x$ for all $x \neq \frac{2}{3}$

$\Rightarrow f o f = 1$

Hence, the given function f is invertible and the inverse of f is itself.

7. Show that the relation R in the set A of all the books in a library of a college, given by R = {(x, y): x and y have same number of pages} is an equivalence relation.

We have,

R= ${(x, y) : x & y$ have same number of pages $}$ is a relation in set of A of all books in

For $(x, y) \in R & x, y \in A$

As x=y=same no. of pages

Then, $(x, x) \in R$

Hence, R is reflexive.

For $(x, y) \in R$ and $x, y \in A$

Also, $(y, x) \in R$ , $∴ x = y$

Hence, R is symmetric.

For $x, y, z \in A$ and $(x, y) \in R$ and $(y, z) \in R$

x=y and y=z

x=z

i.e., $(x, z) \in R$

hence, R is also transitive

$∴$ R is an equivalence relation.

73. Let R → R be the Signum Function defined as $f (x) = {\begin{matrix} 1 & x > 0 \\ 0 & x = 0 \\ - 1 & x < 0 \end{matrix}$ and R → R be the Greatest Function given by g(x) = [x] where [x] is greatest integer less than or equal to x

Then, does fog and gof coincide in (0, 1)?

It is given that,

$f : R \to R$ is defined as $f (x) = {\begin{matrix} 1 & x > 0 \\ 0 & x = 0 \\ - 1 & x < 0 \end{matrix}$

Also, $g : R \to R$ is defined as $g (x) = [x]$ , where [x] is the greatest integer less than or equal to x.

Now, let $x \in (0, 1)$

Then, we have:

$[x] = 1$ if $x = 1$ and $[x] = 0$ if $0 < x < 1$

$\begin{array}{l} ∴ f o g (x) = f (g (x)) = f ([x]) = {\begin{matrix} f (1) & i f, x = 1 \\ f (0) & i f, x \in (0, 1) \end{matrix} = {(1, " i f, x = 1 "), (0, : i f, x \in (0, 1) ") :} \\ g o f (x) = g (f (x)) \\ = g (1) [x > 0] \\ = [1] = 1 \end{array}$

Thus, when $x \in (0, 1)$ , we have $f o g (x) = 0 a n d, g o f (x) = 1 .$

Hence, fog and gof do not coincide in (0, 1).

Therefore, option (B) is correct.

66. Let S = {a, b, c} and T = {1, 2, 3}. Find F⁻¹ of the following functions F from S to T, if it exists.

(i) F = {(a, 3), (b, 2), (c, 1)} (ii) F = {(a, 2), (b, 1), (c, 1)}

S = {a, b, c}, T = {1, 2, 3}

(i) F: S → T is defined as:

F = { (a, 3), (b, 2), (c, 1)}

⇒ F (a) = 3, F (b) = 2, F (c) = 1

Therefore, F⁻¹ : T → S is given by

F⁻¹ = { (3, a), (2, b), (1, c)}.

(ii) F: S → T is defined as:

F = { (a, 2), (b, 1), (c, 1)}

Since F (b) = F (c) = 1, F is not one-one.

Hence, F is not invertible i.e., F⁻¹ does not exist.

69. Define binary operation * on the set {0, 1, 2, 3, 4, 5} as $a * b = {\begin{matrix} a + b & i f, a + b < 6 \\ a + b - 6 & f, a + b \geq 6 \end{matrix}$

Show that zero is the identity for this operation and each element a ≠ 0 of the set is invertible with 6 - abeing the inverse of a

Let X={0, 1, 2, 3, 4, 5}.

The operation* on X is defined as:

$a * b = {\begin{matrix} a + b & i f, a + b < 6 \\ a + b - 6 & i f, a + b \geq 6 \end{matrix}$

An element $e \in X$ is the identity element for the operation*, if $a * e = a = e * a \forall a \in X$

For $a \in X$ we observed that

$\begin{array}{l} a * 0 = a + 0 = a [a \in X \Rightarrow a + 0 < 6] \\ 0 * a = 0 + a = a [a \in X \Rightarrow 0 + a < 6] \\ ∴ a * 0 = 0 * a \forall a \in X \end{array}$

Thus, 0 is the identity element for the given operation*.

An element $a \in X$ is invertible if there exists $b \in X$ such that $a * 0 = 0 * a .$

$i e {\begin{matrix} a + b = 0 = b + a & i f, a + b < 6 \\ a + 6 - 6 = 0 = b + a - 6 & i f, a + b \geq 6 \end{matrix}$

i.e.,

$a = - b, o r, b = 6 - a$

But, X={0, 1, 2, 3, 4, 5} and $a, b \in X$ . Then, $a \neq - b$ .

$∴ b = 6 - a$ is the inverse of $a & m n F o r E; a \in X .$

Hence, the inverse of an element $a \in X, a \neq 0$ is 6-a i.e., $a^{- 1} = 6 - a .$

*	0	1	2	3	4	5
0	0	1	2	3	4	5
1	1	2	3	4	5	0
2	2	3	4	5	0	1
3	3	4	5	0	1	2
4	4	5	0	1	2	3
5	5	0	1	2	3	4

57. Let f: W → W be defined as f(n) = n − 1, if is odd and f(n) = n + 1, if n is even. Show that f is invertible. Find the inverse of f. Here, W is the set of all whole numbers.

It is given that:

$f : W \to W$ is defined as $f (n) = {\begin{cases} n - 1, i f . n, o d d \\ n + 1, i f . n, e v e n \end{cases}$

One-one:

Let, $f (n) = f (m) .$

It can be observed that if n is odd and m is even, then we will have n-1=m+1.

$\Rightarrow n - m = 2$

However, the possibility of n being even and m being odd can also be ignored under a similar argument.

$∴$ Both n and m must be either odd or even.

Now, if both n and m are odd, then we have:

$f (n) = f (m) \Rightarrow n - 1 = m - 1 \Rightarrow n = m$

Again, if both n and m are even, then we have:

$f (n) = f (m) \Rightarrow n + 1 = m + 1 \Rightarrow n = m$

$∴ f$ is one-one.

It is clear that any odd number 2r+1 in co-domain N is the image of 2r in domain N and any even 2r in co-domain N is the image of 2r+1 in domain N.

$∴ f$ is onto.

Hence, f is an invertible function.

Let us define $g : W \to W$ as:

$g (m) = {\begin{cases} m + 1, i f . n, e v e n \\ m - 1, i f . n, o d d \end{cases}$

Now, when n is odd:

$g o f (n) = g (f (n)) = g (n - 1) = n - 1 + 1 = n$

And, when n is even:

$g o f (n) = g (f (n)) = g (n + 1) = n + 1 - 1 = n$

Similarly, when m is odd:

$f o g (m) = f (g (m)) = f (m - 1) = m - 1 + 1 = m$

When m is even:

$\begin{array}{l} f o g (m) = f (g (m)) = f (m + 1) = m + 1 - 1 = m \\ ∴ g o f = I_{W}, a n d, f o g = I_{W} \end{array}$

Thus, f is invertible and the inverse of f is given by $f^{- 1} = g$ , which is the same as f.

Hence, the inverse of f is f itself.

67. Consider the binary operations*: R ×R → and o: R × R → R defined as a * b = |a - b| and ao b = a, &mn For E; a, b ∈ R. Show that * is commutative but not associative, o is associative but not commutative. Further, show that &mn For E;a, b, c ∈ R, a*(b o c) = (a * b) o (a * c). [If it is so, we say that the operation * distributes over the operation o]. Does o distribute over *? Justify your answer.

It is given that*: $R \times R \to$ and $o : R \times R \to R$ is defined as

$a * b = | a - b | a n d, a o b = a, & m n F o r E; a, b \in R .$

For $a, b \in R$ , we have:

$\begin{array}{l} a * b = | a - b | \\ b * a = | b - a | = | - (a - b) | = | a - b | \\ ∴ a * b = b * a \end{array}$

$∴$ The operation* is commutative.

It can be observed that,

$\begin{array}{l} (1.2) . 3 = (| 1 - 2 |) . 3 = 1.3 = | 1 - 3 | = 2 \\ 1 * (2 * 3) = 1 * (| 2 - 3 |) = 1 * 1 = | 1 - 1 | = 0 \\ ∴ (1 * 2) * 3 = 1 * (2 * 3) (w h e r e, 1, 2, 3 \in R) \end{array}$

$∴$ The operation* is not associative.

Now, consider the operation o:

It can be observed that $1 o 2 = 1, a n d, 2 o 1 = 2 .$

$∴ 1 o 2 \neq 2 o 1 (w h e r e, 1, 2 \in R)$

$∴$ The operation o is not commutative.

Let, $a, b, c \in R$ . Then we have:

$\begin{array}{l} (a ο b) ο c = a o c = a \\ a o (b ο c) = a o b = a \\ \Rightarrow (a ο b) ο c = a o (b ο c) \end{array}$

$∴$ The operation o is associative.

Now, $a, b, c \in R$ . Then we have:

$\begin{array}{l} a * (b ο c) = a * b = | a - b | \\ (a * b) o (a * c) = (| a - b |) o (| a - c |) = | a - b | \\ H e n c e, a * (b ο c) = (a * b) o (a * c) . \\ N o w, \\ 1 o (2 ο 3) = 1 o (| 2 - 3 |) = 1 o 1 = 1 \\ (1 o 2) * (1 o 3) = 1 * 1 = | 1 - 1 | = 0 \\ ∴ 1 o (2 ο 3) \neq (1 o 2) * (1 o 3) (w h e r e, 1, 2, 3 \in R) \end{array}$

$∴$ The operation o does not distribute over*.

68. Given a non-empty set X, let *: P(X) × P(X) → P(X) be defined as A * B = (A − B) ∪ (B − A), &mn For E; A, B ∈ P(X). Show that the empty set Φ is the identity for the operation * and all the elements A of P(X) are invertible with A−1 = A. (Hint: (A − Φ) ∪ (Φ − A) = A and (A − A) ∪ (A − A) = A * A = Φ).

It is given that ∗: P (X) × P (X) → P (X) be defined as

A * B = (A – B) ∪ (B – A), A, B ∈ P (X).

Now, let A? P (X). Then, we get,

A *? = (A –? ) ∪ (? –A) = A∪? = A

? * A = (? - A) ∪ (A -? ) =? ∪A = A

A *? = A =? * A, A? P (X)

Therefore? is the identity element for the given operation *.

Now, an element A? P (X) will be invertible if there exists B? P (X) such that

A * B =? = B * A. (as? is an identity element.)

Now, we can see that A * A = (A –A) ∪ (A – A) =? ∪? =? A? P (X).

Therefore, all the element A of P (X) are invertible with A-1 = A.

5. Check whether the relation R in R defined as R = {(a, b): a ≤ b³} is reflexive, symmetric or transitive.

We have,

R= ${(a, b) : a \leq b^{3}}$ is a relation in R.

For, $(a, b) \in R$ and $a = \frac{1}{2}$ we can write

$a \leq a^{3}$ => $\frac{1}{2} \leq {(\frac{1}{2})}^{3}$ => $\frac{1}{2} \leq \frac{1}{8}$ which is not true.

So, R is not reflexive.

For $(a, b) = (1, 2) \in R$ we have,

$a \leq b^{3}$ => $1 \leq 2^{3}$ => $1 \leq 8$ is true.

So, $(1, 2) \in R$

But $2 \leq 1^{3}$ => $2 \leq 1$ is not true

So, $(2, 1) \notin R$ and $(b, a) \notin R$

Hence, R is not symmetric.

For, $(a, b) = (10, 4)$ and $(b, c) = (4, 2) \in R$

$10 \leq 4^{3}$ => $10 \leq 64$ is true=> $(10, 4) \in R$

$4 \leq 2^{3}$ => $4 \leq 8$ is true=> $(4, 2) \in R$

But $10 \leq 2^{3}$ => $10 \leq 8$ is not true=> $(10, 2) \notin R$

Hence, for $(a, b), (b, c) \in R, (a, c) \notin R$

So, R is not transitive.

11. Show that the relation R in the set A of points in a plane given by R = {(P, Q): distance of the point P from the origin is same as the distance of the point Q from the origin}, is an equivalence relation. Further, show that the set of all point related to a point P ≠ (0, 0) is the circle passing through P with origin as centre.

The given relation in set A of points in a plane is

R= ${(P, Q) :$ distance of point P from origin=distance of point Q from $o r i g i n}$

If O is the point of origin

R= ${(P, Q) : P O = Q O}$

Then, for $P \in A$ we have PO=PO

So, $(P, P) \in R$

i.e., P is reflexive

for, $P, Q \in A$ and $(P, Q) \in R$ we have

PO=QO

QO=PO i.e., $(Q, P) \in R$

i.e., R is symmetric

for $P, Q, S \in A$ and $(P, Q) & (Q, S) \in R$

PO=QO and QO=SO

PO=SO

i.e., $(P, S) \in R$

so, R is transitive

Hence, R is an equivalence relation

For a point $P \neq (o, o)$ the set of all points related to P i.e., distance from origin to the points are equal is a circle with center at origin (o, o) by the definition of circle

15. Let R be the relation in the set {1, 2, 3, 4} given by R = {(1, 2), (2, 2), (1, 1), (4, 4), (1, 3), (3, 3), (3, 2)}. Choose the correct answer.

(A) R is reflexive and symmetric but not transitive.

(B) R is reflexive and transitive but not symmetric.

(C) R is symmetric and transitive but not reflexive.

(D) R is an equivalence relation.

The set in $A = {1, 2, 3, 4}$

The relation in this set $A$ is given by

$R = {(1, 2), (2, 2), (1, 1), (4, 4), (1, 3), (3, 3), (3, 2)}$

$R$ is reflexive as $(1, 1), (2, 2), (3, 3), (4, 4) \in R$

As, $(1, 2) \in R$ but $(2, 1) \notin R$

$R$ is not symmetric

For $(1, 2) \in R$ and $(2, 2) \in R; (1, 2) \in R$

And for $(1, 3) \in R$ and $(3, 2) \in R; (1, 3) \in R$

∴ $R$ is transitive

Hence, option (B) is correct

22. Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from A to B. Show that f is one-one.

Given, $f : A \to B$ and $f = {(1, 4), (2, 5), (3, 6)}$

$\begin{array}{l} ∴ f (1) = 4 \\ f (2) = 5 \\ f (3) = 6 \end{array}$

i.e., the image elements of $A$ under the given $f_{X}^{n}$ $f$ are unique

So, $f$ is one-one

24. Let A and B be sets. Show that f: A × B → B × A such that (a, b) = (b, a) is bijective function.

Given, $f : A \times B \to B \times A$ defined as $f (a, b) = (b, a)$

Let $(a_{1}, b_{1}), (a_{2}, b_{2}) \in A \times B$ such that

$f (a_{1}, b_{1}) = f (a_{2}, b_{2})$

$\Rightarrow (b_{1}, a_{1}) = (b_{2}, a_{2})$

So, $b_{1} = b_{2}$ and $a_{1} = a_{2}$

$\Rightarrow (a_{1}, b_{1}) = (a_{2}, b_{2})$

$∴ f$ is one-one

For $(a, b) \in B \times A$

There exist $(a, b) \in A \times B$ such that $f (a, b) = (b, a)$

$∴ f$ is onto

Hence, $f$ is bijective

13. Show that the relation R defined in the set A of all polygons as R = {(P₁, P₂): P_{1 and} P₂ have same number of sides}, is an equivalence relation. What is the set of all elements in A related to the right-angle triangle T with sides 3, 4 and 5?

The given relation in set A of all polygons is defined as

R= ${(P_{1}, P_{2}) : P_{1}$ and $P_{2}$ have same number of sides $}$

Let $P_{1} \in A$ ,

As number of sides $(P_{1})$ = number of sides $(P_{1})$

$(P_{1}, P_{1}) \in R$

So, R is reflexive.

Let $P_{1}, P_{2} \in A$ and $(P_{1}, P_{2}) \in R$

Then, number of sides of $P_{1}$ = number of sides of $P_{2}$

Number of sides of $P_{2}$ = number of sides of $P_{1}$

i.e., $(P_{2}, P_{1}) \in R$

so, R is symmetric.

Let $P_{1}, P_{2}, P_{3} \in A$ and $(P_{1}, P_{2})$ and $(P_{2}, P_{3}) \in R$

Then, number of sides $(P_{1})$ = number of sides $(P_{2})$

Number of sides $(P_{2})$ = number of sides $(P_{3})$

So, number of sides $(P_{1})$ = number of sides $(P_{3})$

I.e., $(P_{1}, P_{3}) \in R$

So, R is transitive.

Hence, R is an equivalence relation.

The set of all triangles will be the elements in A related to the right-angle triangle T with sides 3,4 and 5 as they all have three number of sides.

14. Let L be the set of all lines in XY plane and R be the relation in L defined as R = {(L₁, L₂): L₁ is parallel to L₂}. Show that R is an equivalence relation. Find the set of all lines related to the line y = 2x + 4.

The given relation in the set $L =$ all lines in $X Y -$ plane is defined as

$R = {(L_{1}, L_{2}) : L_{1}$ is parallel to $L_{2}}$

Let $L_{1} \in A$ then as $L_{1}$ is parallel to $L_{1}$ ,

$(L_{1}, L_{1}) \in R$

So, $R$ is reflexive

Let $L_{1}, L_{2} \in A$ and $(L_{1}, L_{1}) \in R$

Then, $L_{1}$ is parallel to $L_{2}$

$L_{2}$ is parallel to $L_{1}$

So, $(L_{2}, L_{1}) \in R$

i.e., $R$ is symmetric

Let $L_{1}, L_{2}, L_{3} \in A$ and $(L_{1}, L_{2})$ and $(L_{2}, L_{3}) \in R$

Then, $L_{1} ? L_{2}$ and $L_{2} ? L_{3}$

So, $L_{1} ? L_{3}$

i.e., $(L_{1}, L_{2}) \in R$

So, $R$ is transitive

Hence, $R$ is an equivalence relation

The set of lines related to $y = 2 x + 4$ is given by the equation $y = 2 x + C$ where $C$ is some constant.

4. Show that the relation R in R defined as R = {(a, b): a ≤ b}, is reflexive and transitive but not symmetric.

We have, R= ${(a, b) : a \leq b}$ is a relation in R.

For, $a \in R$ ,

$a \leq b$ but $b \leq a$ is not possible i.e., $(b, a) \notin R$

Hence, R is not symmetric.

For $(a, b) \in R & (b, c) \in R$ and $a, b, c \in R$

$a \leq b$ and $b \leq c$

So, $a \leq c$

i.e., $(a, c) \in R$

$∴$ R is transitive.

34. Show that f: [-1, 1] → R given by f(x) = x/x+2 is one-one. Find the inverse of the function f: [-1, 1] → Range f

$f : [- 1, 1] \to R$ is given as $f (x) = \frac{x}{x + 2}$

$\begin{array}{l} L e t, f (x) = f (y) . \\ \Rightarrow \frac{x}{x + 2} = \frac{y}{y + 2} \\ \Rightarrow x y + 2 x = x y + 2 y \\ \Rightarrow 2 x = 2 y \\ \Rightarrow x = y \end{array}$

$∴$ f is a one-one function.

It is clear that $f : [- 1, 1] \to$ Range f is onto.

$∴$ $f : [- 1, 1] \to$ Range f is one-one onto and therefore, the inverse of the function:

$f : [- 1, 1] \to$ Range f exists.

Let g: Range $f \to [- 1, 1]$ be the inverse of f.

Let y be an arbitrary element of range f.

Since $f : [- 1, 1] \to$ Range f is onto, we have:

$\begin{array}{l} \Rightarrow y = \frac{x}{x + 2} \\ \Rightarrow x y + 2 y = x \\ \Rightarrow x (1 - y) = 2 y \\ \Rightarrow x = \frac{2 y}{1 - y}, y \neq 1 \\ g (y) = \frac{2 y}{1 - y}, y \neq 1 \\ N o w, (g o f) (x) = g (f (x)) = g (\frac{x}{x + 2}) = \frac{2 (\frac{x}{x + 2})}{1 - \frac{x}{x + 2}} = \frac{2 x}{x + 2 - x} = 2 \frac{x}{2} = x \\ (f o g) (y) = f (g (y)) = f (\frac{2 y}{1 - y}) = \frac{\frac{2 y}{(1 - y)}}{(\frac{2 y}{1 - y}) + 2} = \frac{2 y}{2 y + 2 - 2 y} = \frac{2 y}{2} = y \\ ∴ g o f = I_{- 1, 1}, a n d, f o g - I_{R a n g e, f} \\ ∴ f^{- 1} = g \\ ∴ f^{- 1} (y) = \frac{2 y}{1 - y}, y \neq 1 \end{array}$

36. Consider f: R+ → [4, ∞) given by f(x) = x² + 4 Show that f is invertible with the inverse f⁻¹ of f given by f⁻¹(y) = √y - 4 where R+ is the set of all non-negative real numbers.

$f : R_{+} \to [4, \infty)$ is given as $f (x) = x^{2} + 4$ .

One-one:

$\begin{array}{l} L e t, f (x) = f (y) . \\ \Rightarrow x^{2} + 4 = y^{2} + 4 \\ \Rightarrow x^{2} = y^{2} \\ \Rightarrow x = y [a s, x = y \in R] \end{array}$

$∴ f$ is a one-one function.

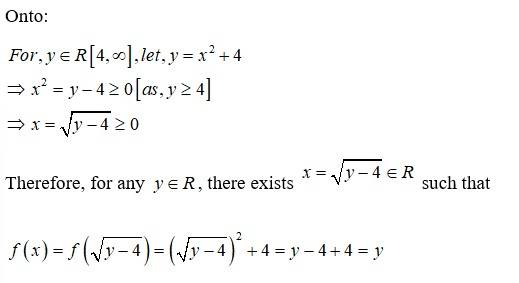
62. Given examples of two functions f: N → N and g: N → N such that gof is onto but f is not onto.

(Hint: Consider f(x) = x + 1 and $g (x) {\begin{matrix} x - 1 & i f, x > 1 \\ 1 & f, x = 1 \end{matrix}}$

Define $f : Ν \to Ν$ by

$f (x) = x + 1$

And, $g : Ν \to Ν$ by,

$g (x) {\begin{matrix} x - 1 & i f, x > 1 \\ 1 & f, x = 1 \end{matrix}}$

We first show that g is not onto.

For this, consider element 1 in co-domain N. it is clear that this element is not an image of any of the elements in domain.

$∴ f$ is not onto.

Now, $g o f : Ν \to Ν$ is defined by,

$\begin{array}{l} g o f (x) = g (f (x)) = g (x + 1) = (x + 1) - 1 [x, i n Ν = > (x + 1) > 1] \\ = x \end{array}$

Then, it is clear that for $y \in Ν$ , there exists $x = y \in Ν$ such that $g o f (x) = g o f (y)$

Hence, gof is onto.

65. Find the number of all onto functions from the set {1, 2, 3, … , n) to itself.

Onto functions from the set {1, 2, 3, …, n} to itself is simply a permutation on n symbols 1, 2, …, n.

Thus, the total number of onto maps from {1, 2, …, n} to itself is the same as the total number of permutations on n symbols 1, 2, …, n, which is n!

38. Let f: X → Y be an invertible function. Show that f has unique inverse.

(Hint: suppose g₁ and g₂ are two inverses of f. Then for all y ∈ Y, fog₁(y) = IY(y) = fog₂(y). Use one-one ness of f).

Let $f : X \to Y$ be an invertible function.

Also, suppose f has two inverses (say g₁ and g₂ ).

Then, for all y ∈ Y, we have:

$\begin{array}{l} f o g_{1} (y) = I_{y} (y) = f o g_{2} (y) \\ \Rightarrow f (g_{1} (y)) = f (g_{2} (y)) \end{array}$ [f is invertible => f is one-one]

$\Rightarrow g_{1} = g_{2}$ [g is one-one]

Hence, f has a unique inverse.

40. Let f: X → Y be an invertible function. Show that the inverse of f−1 is f, i.e., (f⁻¹)⁻¹ = f.

Let f: X → Y be an invertible function.

Then, there exists a function g: Y → X such that gof = IX and fog = IY.

Here, f⁻¹ = g.

Now, gof = IX and fog = IY

⇒ f⁻¹ of = IX and fof⁻¹ = IY

Hence, f⁻¹ : Y → X is invertible and f is the inverse of f⁻¹

i.e., (f−1)⁻¹ = f.

45. Consider the binary operation ∨ on the set {1, 2, 3, 4, 5} defined by a ∨b = min {a, b}. Write the operation table of the operation∨.

The binary operation? on the set {1, 2, 3, 4, 5} is defined as a? b = min {a, b} &mn For E; a, b? {1, 2, 3, 4, 5}.

Thus, the operation table for the given operation? can be given as:

?	1	2	3	4	5
1	1	1	1	1	1
2	1	2	2	2	2
3	1	2	3	3	3

4	1	2	3	4	4
5	1	2	3	4	5

47. Let*′ be the binary operation on the set {1, 2, 3, 4, 5} defined by a *′ b = H.C.F. of a and b. Is the operation *′ same as the operation * defined in Exercise 4 above? Justify your answer.

The binary operation *′ on the set {1, 2, 3 4, 5} is defined as a *′ b = H.C.F of a and b.

The operation table for the operation *′ can be given as:

*′	1	2	3	4	5
1	1	1	1	1	1

2	1	2	1	2	1
3	1	1	3	1	1
4	1	2	1	4	1
5	1	1	1	1	5

We observe that the operation tables for the operations * and *′ are the same.

Thus, the operation *′ is same as the operation*.

48. Let * be the binary operation on N given by a * b = L.C.M. of a and b. Find

(i) 5 * 7, 20 * 16 (ii) Is * commutative?

(iii) Is * associative? (iv) Find the identity of * in N

(v) Which elements of N are invertible for the operation *?

The binary operation * on N is defined as a * b = L.C.M. of a and b.

(i) 5 * 7 = L.C.M. of 5 and 7 = 35

20 * 16 = L.C.M of 20 and 16 = 80

(ii) It is known that:

L.C.M of a and b = L.C.M of b and a & mnForE; a, b ∈ N.

∴a * b = b * a

Thus, the operation * is commutative.

(iii) For a, b, c ∈ N, we have:

(a * b) * c = (L.C.M of a and b) * c = LCM of a, b, and c

a * (b * c) = a * (LCM of b and c) = L.C.M of a, b, and c

∴ (a * b) * c = a * (b * c)

Thus, the operation * is associative.

(iv) It is known that:

L.C.M. of a and 1 = a = L.C.M. 1 and a &mnForE; a ∈ N

⇒ a * 1 = a = 1 * a &mnForE; a ∈ N

Thus, 1 is the identity of * in N.

(v) An element a in N is invertible with respect to the operation * if there exists an element b in N, such that a * b = e = b * a.

Here, e = 1

This means that:

L.C.M of a and b = 1 = L.C.M of b and a

This case is possible only when a and b are equal to 1.

Thus, 1 is the only invertible element of N with respect to the operation *.

49. Is * defined on the set {1, 2, 3, 4, 5} by a * b = L.C.M. of a and b a binary operation? Justify your answer.

The operation * on the set A = {1, 2, 3, 4, 5} is defined as

a * b = L.C.M. of a and b.

Then, the operation table for the given operation * can be given as:

*	1	2	3	4	5
1	1	2	3	4	5
2	2	2	6	4	10
3	3	6	3	12	15
4	4	4	12	4	20
5	5	10	15	20	5

It can be observed from the obtained table that:

3 * 2 = 2 * 3 = 6 ∉ A, 5 * 2 = 2 * 5 = 10 ∉ A, 3 * 4 = 4 * 3 = 12 ∉ A

3 * 5 = 5 * 3 = 15 ∉ A, 4 * 5 = 5 * 4 = 20 ∉ A

Hence, the given operation * is not a binary operation.

50. Let * be the binary operation on N defined by a * b = H.C.F. of a and b. Is * commutative? Is * associative? Does there exist identity for this binary operation on N?

The binary operation * on N is defined as:

a * b = H.C.F. of a and b

It is known that:

H.C.F. of a and b = H.C.F. of b and a & mn For E; a, b ∈ N.

∴a * b = b * a

Thus, the operation * is commutative.

For a, b, c ∈ N, we have:

(a * b)* c = (H.C.F. of a and b) * c = H.C.F. of a, b, and c

a * (b * c)= a * (H.C.F. of b and c) = H.C.F. of a, b, and c

∴ (a * b) * c = a * (b * c)

Thus, the operation * is associative.

Now, an element e ∈ N will be the identity for the operation * if a * e = a = e* a ∈ a ∈ N.

But this relation is not true for any a ∈ N.

Thus, the operation * does not have any identity in N.

52. Find which of the operations given above has identity.

Let the identity be I.

An element $e \in Q$ will be the identity element for the operation* if

$a * e = a = e * a, \forall a \in Q .$

We are given

$\begin{array}{l} a * b = a b 4 \\ \Rightarrow a * e = a \Rightarrow a e 4 = a \Rightarrow e = 4 \end{array}$

Similarly, it can be checked for $e * a = a$ , we get e=4. Thus, e=4 is the identity

53. Let A = N × N and * be the binary operation on A defined by

(a, b) * (c, d) = (a + c, b + d)

Show that * is commutative and associative. Find the identity element for * on A, if any.

A = N × N

* is a binary operation on A and is defined by:

(a, b) * (c, d) = (a + c, b + d)

Let (a, b), (c, d) ∈ A

Then, a, b, c, d ∈ N

We have:

(a, b) * (c, d) = (a + c, b + d)

(c, d) * (a, b) = (c + a, d + b) = (a + c, b + d)

[Addition is commutative in the set of natural numbers]

∴(a, b) * (c, d) = (c, d) * (a, b)

Therefore, the operation * is commutative.

Now, let (a, b), (c, d), (e, f) ∈A

Then, a, b, c, d, e, f ∈ N

We have:

$\begin{array}{l} ((a, b) . (c, d)) . (e, f) = (a + c, b + d) . (e, f) = (a + c + e, b + d + f) \\ (a, b) . ((c, d) . (e, f)) = (a, b) . (c + e, d + f) = (a + c + e, b + d + f) \\ ∴ ((a, b) . (c, d)) . (e, f) = (a, b) . ((c, d) . (e, f)) \end{array}$

Therefore, the operation* is associative.

An element $e = (e_{1}, e_{2})$ will be an identity element for the operation* if

$a * e = a = e * a \forall a = (a_{1}, a_{2}) \in A$

$i . e ., (a_{1} + e_{1}, a_{2} + e_{2}) = (a_{1}, a_{2}) = (e_{1} + a_{1}, e_{2} + a_{2})$ which is not true for any element in A.

Therefore, the operation* does not have any identity element.

Which is not true for any element in A.

Therefore, the operation * does not have any identity element.

55. Consider a binary operation * on N defined as a * b = a³ + b³. Choose the correct answer.

(A) Is * both associative and commutative?

(B) Is * commutative but not associative?

(C) Is * associative but not commutative?

(D) Is * neither commutative nor associative?

On N, the operation * is defined as a * b = a³ + b³.

For, a, b, ∈ N, we have:

a * b = a³ + b³ = b³ + a³ = b * a [Addition is commutative in N]

Therefore, the operation * is commutative.

It can be observed that:

(1*2)*3 = (1³+2³)*3 = 9 * 3 = 93 + 33 = 729 + 27 = 756

Also, 1* (2*3) = 1* (2³+3³) = 1* (8 +27) = 1 × 35

= 1³ +35³ = 1 + (35)³ = 1 + 42875 = 42876.

∴ (1 * 2) * 3 ≠ 1 * (2 * 3) ; where 1, 2, 3 ∈ N

Therefore, the operation * is not associative.

Hence, the operation * is commutative, but not associative. Thus, the correct answer is B.

64. Given a non-empty set X, consider the binary operation *: P(X) × P(X) → P(X) given by A * B = A ∩ B &mn For E; A, B in P(X) is the power set of X. Show that X is the identity element for this operation and X is the only invertible element in P(X) with respect to the operation*.

Let S be a non-empty set and P (S) be its power set. Let any two subsets A and B of S.

It is given that: $P (X) x P (X) \to P (X)$ is defined as $A . B = A \cap B \forall A, B \in P (X)$

We know that $A \cap X = A = X \cap A \forall A \in P (X)$

$\Rightarrow A . X = A = X . A \forall A \in P (X)$

Thus, X is the identity element for the given binary operation*.

Now, an element is $A \in P (X)$ invertible if there exists $B \in P (X)$ such that

$A * B = X = B * A$ (As X is the identity element)

i.e.

$A \cap B = X = B \cap A$

This case is possible only when $A = X = B .$

Thus, X is the only invertible element in P (X) with respect to the given operation*.

Hence, the given result is proved.

Find gof and fog , if:

(i) f(x) = |x| and g(x) = |5x - 2|

(ii) f(x) = 8x³ and g(x) = x^1/3

Kindly go through the solution

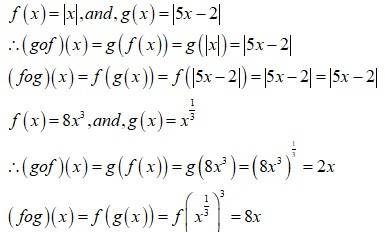
Maths Ncert Solutions class 12th Exam

Student Forum

Anything you would want to ask experts?

Write here...

Other Similar chapters for you

News & Updates

Latest NewsPopular News

Class 12 Maths Chapter 1 NCERT Solutions: Relations and Functions Explained

Glance at Class 12 Maths Chapter 1 Solutions

Class 12 Maths Relations and Functions: Key Topics, Weightage

Relations and Functions Class 12 Weightage in JEE Mains

Important Formulas of Relations and Functions Class 12

Relation and Function Important Formulae for CBSE and Competitive Exams

Functions

Try these practice questions

Class 12 Math Chapter 1 Relation and Function Solution PDF

More Links

Class 12 Math Relation and Function Exercise -wise solutions

Maths Class 12 Relation and Function Exercise 1.1 Solutions

Relation and Function exercise 1.1 solutions

Commonly asked questions

Relation and Function Exercise 1.2 Solutions

Relation and Function Exercise 1.3 Solutions

Student Forum

Other Similar chapters for you

News & Updates

JEE Mains Registration 2026 Live: NTA Form Soon at jeemain.nta.nic.in; Notification, Dates, Syllabus

Tamil Nadu 10th, 12th Public Time Table 2026 Soon @dge.tn.gov.in; Check Live Updates on TN SSLC, Plus Two Dates

UPPSC PCS 2025 Prelims Answer Key Download Link (Official PDF) @uppsc.up.nic.in Live Updates

SSLC, Plus Two Time Table 2026 Kerala Board Soon; Live Updates on Kerala SSLC, Plus Two Exam Time Table

JEE Main Marks vs Percentile vs Rank 2025: Calculate Percentile and Rank Using Marks

List of NIT Colleges in India 2025 - NIRF Ranking, Courses, Seats, Cutoff, Fees and Placement

CBSE 10th Maths Question Paper 2025, 2024, 2023, 2022, 2020, 2019 PDF Download

NEET Chapter Wise Weightage 2026 PDF by NTA: Physics, Chemistry & Biology

List of Top IITs in India 2025: NIRF Ranking, Courses, Seats, Fees & Placement