
Application of Integrals Class 12 Maths chapter deals with the study of a specific application of integrals to find the area between lines, the area under simple curves, the area between arcs of circles, ellipses, and parabolas. Areas under the curve are known as the elementary area.
Applications of Integrals Class 12 is created by the subject matter experts at Shiksha, hence it is reliable and accurate study material for students preparing for the CBSE Board exam and competitive exams like JEE Mains. The solution is created in a step-by-step format, which is easy to understand and gives students deep concept clarity.
Those who are looking for topic-wise revision PDFs with solutions must explore - Class 12 Maths Notes PDF for CBSE Exams.
Related Links
| NCERT Notes for Class 11 & 12 | Class 12 Maths NCERT Solutions | NCERT Solutions Class 11 and 12 |
- Dive into Class 12 Integral Applications
- Class 12 Maths Chapter 8 Application of Integrals NCERT Solutions PDF Download
- Class 12 Math Chapter 8 Application of Integrals : Key Topics, Weightage
- Important Formulas for Class 12 Application of Integrals
- Class 12th Math Exercise 8.1 Solutions
- Topics Covered in NCERT Maths Class 12 Application of Integrals Chapter
Dive into Class 12 Integral Applications
Here are quick highlights of the Integral Applications Class 12 Maths:
- For the curve y = f (x), x-axis and the lines x = a and x = b (b > a), area is -
- For the curve x = φ (y), y-axis and the lines y = c, y = d, area is -
Class 12 Maths Chapter 8 Application of Integrals NCERT Solutions PDF Download
The Application of Integrals Class 12 Solutions PDF link is given below. Download the PDF from the link to prepare well for the CBSE Board exams and other entrance tests.
Download Here: NCERT Solution for Class XII Maths Application of Integrals PDF
If you are looking for quick revision notes of Class 12 Physics, Chemistry, and Maths, then check - NCERT Class 12 Notes.
Class 12 Math Chapter 8 Application of Integrals : Key Topics, Weightage
If you are aiming to score high in an entrance exam such as JEE Mains, you should focus on practicing Class 12 Application of Integrals. It is a small chapter. Below are the topics covered in this chapter:
| Exercise | Topics Covered |
|---|---|
| 8.1 | Introduction |
| 8.2 | Area under Simple Curves |
Application of Integrals Class 12 Weightage in JEE Mains
| Exam | Number of Questions | Weightage |
|---|---|---|
| JEE Main | 1-2 questions | 6-7% |
Important Formulas for Class 12 Application of Integrals
Important Formulae for Class 12 Application of Integrals
-
Area under a curve:
(For a function between and )
-
Area between two curves:
(Where and are two functions and in the given interval)
-
For curves in terms of y:
(Where curves are given in the form and , and in the given interval)
-
Area Enclosed by the x-axis and the Curve:
Class 12th Math Exercise 8.1 Solutions
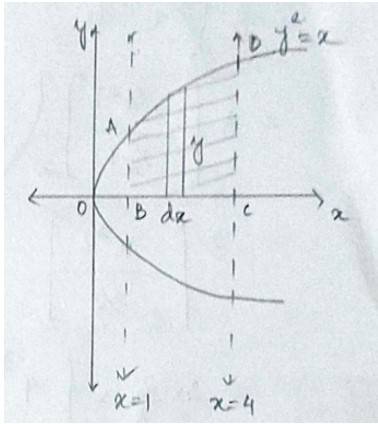
| Q1. Find the area of the region bounded by the curve y² = x the lines x=1, x = 4 and x-axis.
|
| Q2. Find the area of the region bounded by the curve y² = 9x and the lines x=2,x=4 and x-axis in the first quadrant. |
| Q3. Find the area of the region bounded by the curve x² = 4y ,y=2,y=4 and y-axis is the first quadrant. |
| Q4. Find the area of the region bounded by the ellipse . |
Commonly asked questions
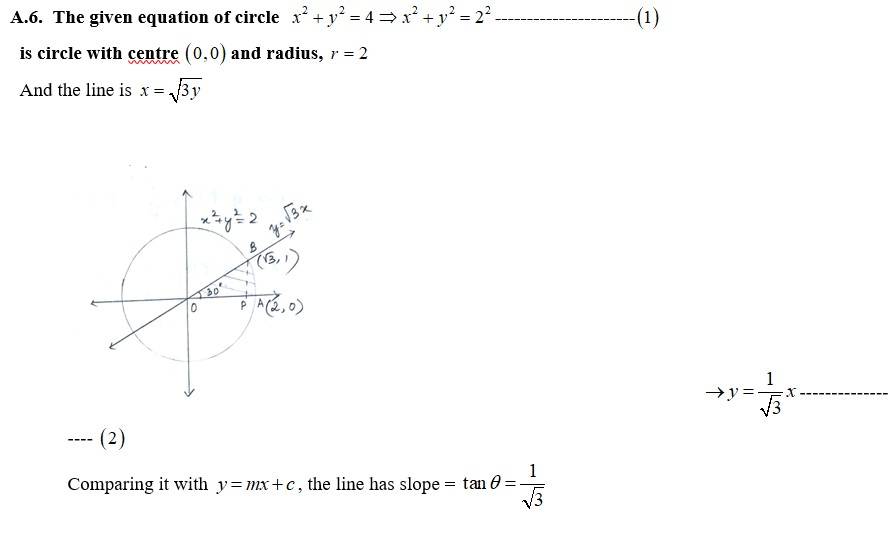
6. Find the area of the region in the first quadrant enclosed by x-axis,line and the circle .
Kindly go through the solution

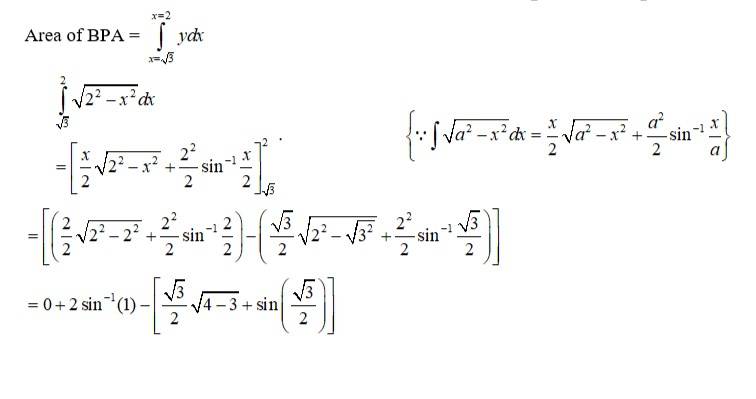
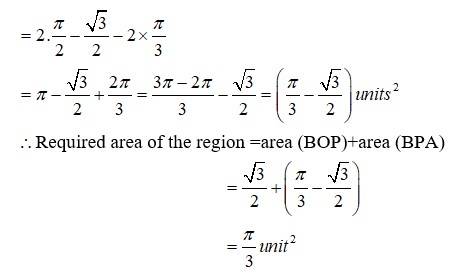
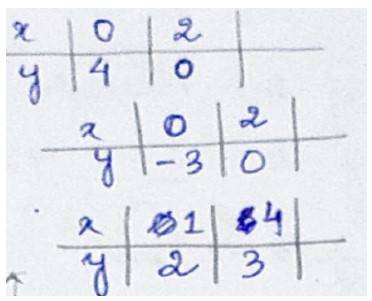
33. Using the method of integration, find the area of the triangle whose vertices are A (2, 0), B (4, 5) and C (6, 3).
The given vertices of the triangle are A(2,0),B(4,5)and C(6,3)
So, equation of line AB is
Similarly equation of BC is
And equation of AC is
=
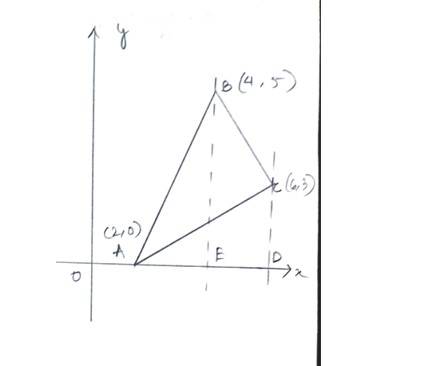
Area of
=
34. Using the method of integration, find the area of the region bounded by the lines: 2x + y = 4, 3x – 2y = 6 and x – 3y + 5 = 0
The given equation of the lines are
Area of

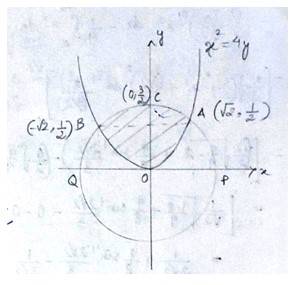
The point of intersection of the circle and the parabola is .
Taking in first quadrant
Area of
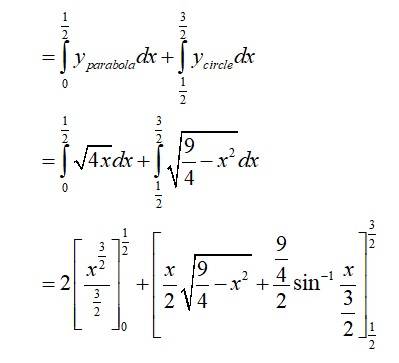

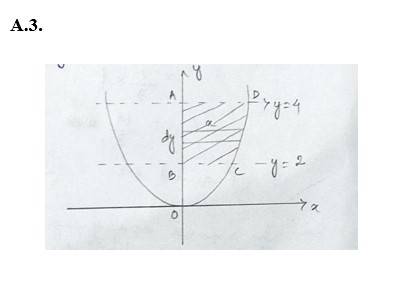
3. Find the area of the region bounded by the curve x² = 4y ,y=2,y=4 and y-axis is the first quadrant.
Kindly go through the solution
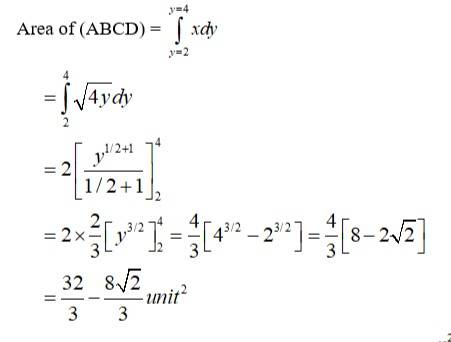
5. Find the area of the region bounded by the ellipse
Kindly go through the solution

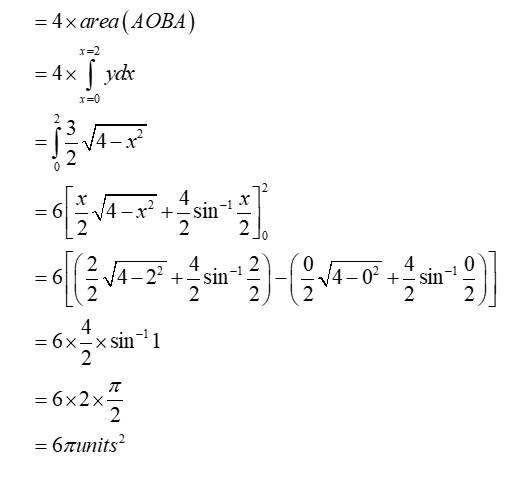
12. Choose the correct answer:
Area lying in the first quadrant and bounded by the circle x² + y² = 4 and the lines x = 0 and x = 2 is
(A) π
(B) π/2
(C) π/3
(D) π/4
Given equation of the circle is

1. Find the area of the region bounded by the curve y² = x the lines x=1, x = 4 and x-axis.
Kindly go through the solution
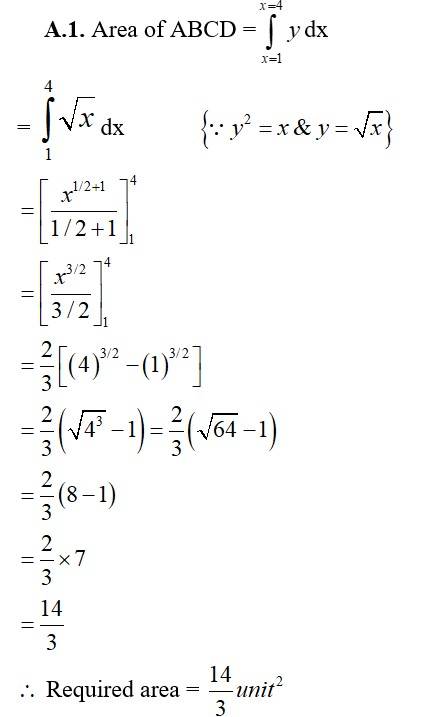
2. Find the area of the region bounded by the curve y² = 9x and the lines x=2,x=4 and x-axis in the first quadrant.
Kindly go through the solution
4. Find the area of the region bounded by the ellipse .
Kindly go through the solution

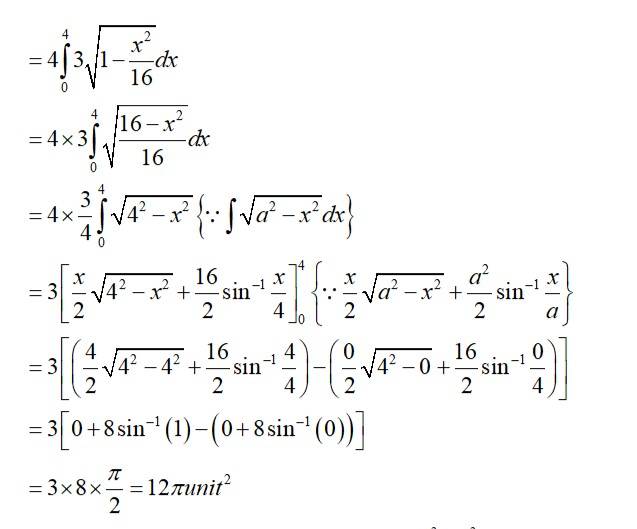
14. Find the area of the circle 4x2 + 4y2 = 9 which is interior to the parabola x2 = 4y
The equation given circle is
i.e, centre (0,0), radius
since intersect the circle
we can put in
which is not possible or cannot be (-)ve


7. Find the area of the smaller part of the circle x² + y² = a² cut off by the line x = a/√2
Kindly go through the solution


8. The area between x = y² and x = 4 is divided into two equal parts by the line x = a find the value of a
Kindly go through the solution
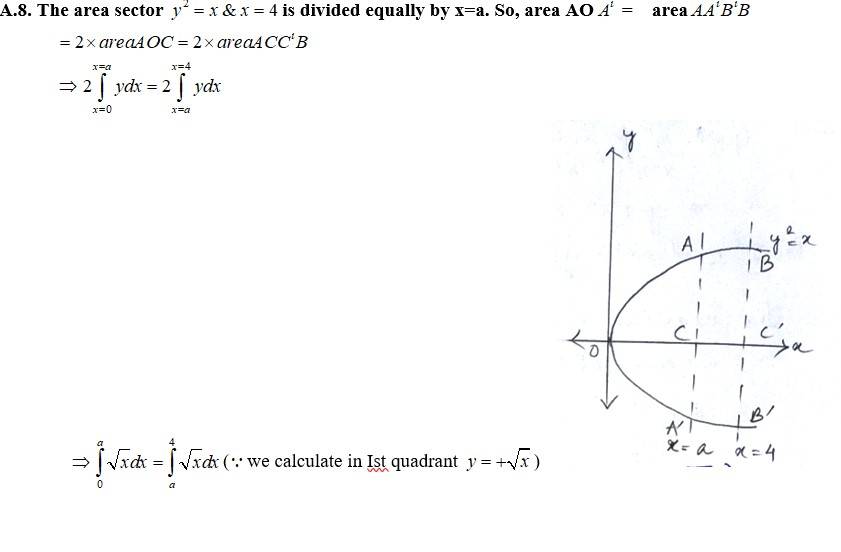
(Squaring both sides)
(Taking cube on both sides)
9. Find the area of the region bounded by the parabola y = x² and y = |x|
Given that equation of
curve
line
Since the line passes through A&B in Ist and IInd quadrants
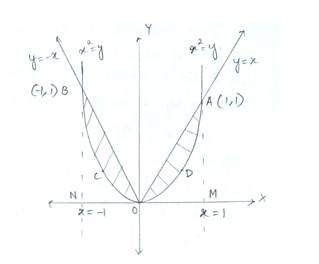
the equation must satisfy
for Ist quadrant and
for IInd t quadrant
So, and
and
i.e, A has coordinate (1,1)
i.e, B has coordinate (1,1)
Now, area of AODA = area (AOM)-area (ADOM)
The required area of the region bounded by curve and line is
10. Find the area bounded by the curve x = 4y and the line x = 4y -2
Given curve is and the equation of line is
The point of intersection of the curve and the line can be determine as follows.
Put,
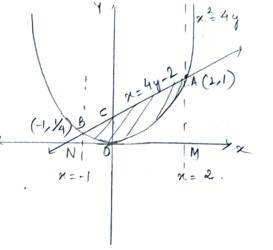
In to determine value of x
i.e,
and
, we have
And at we have
So, the coordinates A and B are (2,1) and ( )
The required area before the line & the curve is area = area of trapezium (BNMAB)- area under curve BDA
11. Find the area of the region bounded by the curve y² = 4x and the line x = 3.
The given equation of the curve is
in Ist quadrant
So, area of curve enclosed by
And area (AOCA)
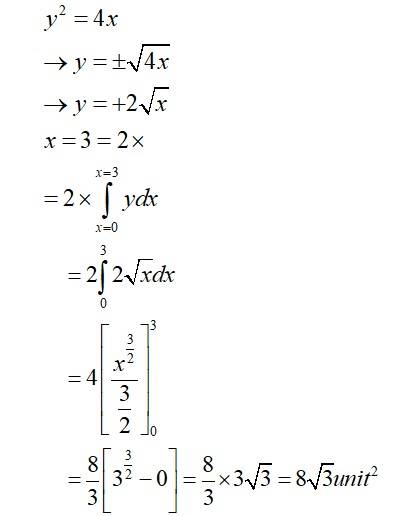
13. Choose the correct answer:
Area of the region bounded by the curve y² = 4x,y - axis and the line y = 3 is:
(A) 2
(B) 9/4
(C) 9/3
(D) 9/2
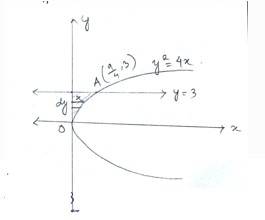
As intersect at Athen,
A has coordinate
Hence, area of curve =
Option (B) is correct
15. Find the area bounded by curves (x – 1)2 + y2 = 1 and x2 + y 2 = 1
The equation of the given circle is
- (1)
- (1) - (2)
Equation (1) is a circle with centre 0 (0,0) and radius 1. Equation (2) is a circle with centre c (1,0) and radius 1.
Solving (1) and (2)
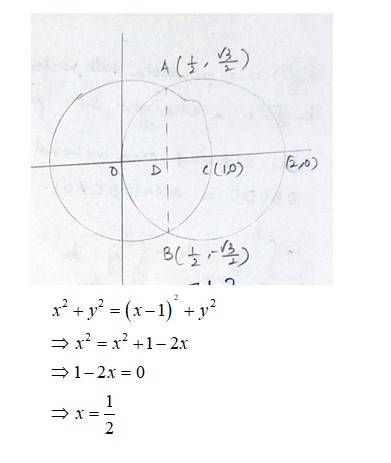


16. Find the area of the region bounded by the curves y = x2 +2, y = x,
x = 0 and x = 3
The equation of the curve is - (1) and
lines are
- (2)
- (3)
- (4)
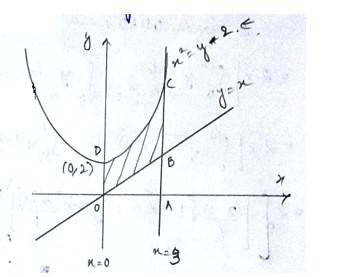
Equation (1)is a parabola with vertex (0,2)
Equation (2)is a straight line passing origin with shape =
The required area enclosed OBCDO = area (ODCAO)-area (OBAO)
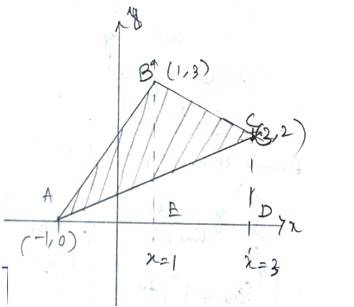
17. Using integration, find the area of the region bounded by the triangle whose vertices are (–1, 0), (1, 3) and (3, 2).
Let A (-1,0),B(1,3) and C (3,2) be the vertices of a triangle ABC
So, equation of line AB is
-------------(1)
Equation of line BC is
---------------(2)
Equation of line AC is
------------------------------(3)
Area of ABC= area ( )
18. Using integration, find the area of the triangular region whose sides have the equations y = 2x +1, y = 3x + 1 and x = 4.
The given equation of the sides of triangle is
--------------------(1)
-------------------(2)
-------------------------(3)
Solving eqn (1) and (2) for x & y we get
The point of inersection of line (1)and (2)is A (0,1)
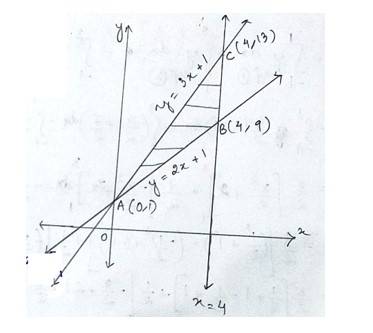
Putting x=4 in eq (1) and (2)we get,
The point of intersection of line (1)and (3) is B(4,9) and C (4,13)
Hence the required area enclosed ABC
19. Choose the correct answer:
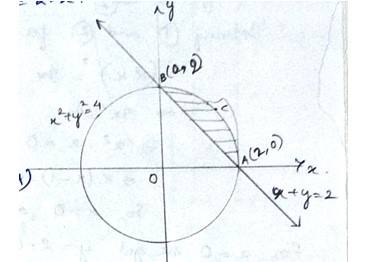
Smaller area enclosed by the circle x2 + y2 = 4 and the line x + y = 2 is
(A) 2 (π – 2)
(B) π – 2
(C) 2π – 1
(D) 2 (π + 2)
The equation of circle is which has centre at (0,0) & radius,
And the line
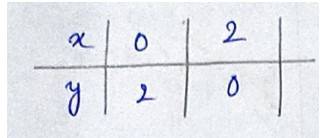
The smaller area of circle is given by
Area (ABCA) area (BOAB) – area (BOA)

20. Choose the correct answer:
Area lying between the curves y2 = 4x and y = 2x is
(A) 2/3
(B) 1/3
(C) 1/4
(D) 3/4
The given equation of the curve is - (1) and
the line is - (2)
Solving (1) and (2) for x and y
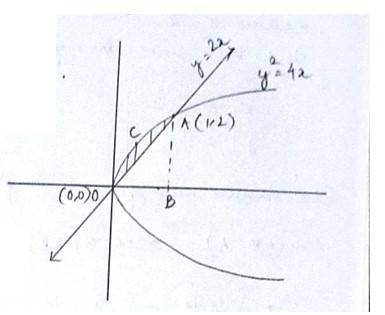
So,
for we get
for , we get
so, the point of intersection are (0,0)and (1,2)
area (DCAO)=area (DCABO)-area ( )
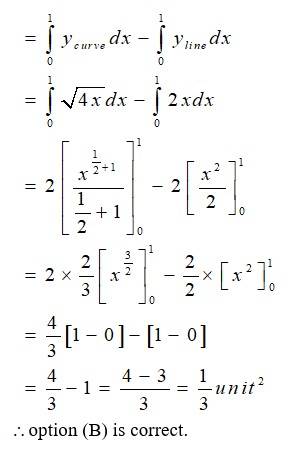
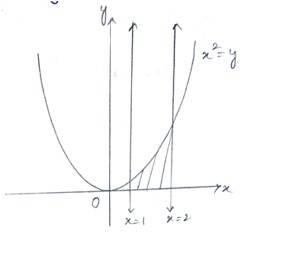
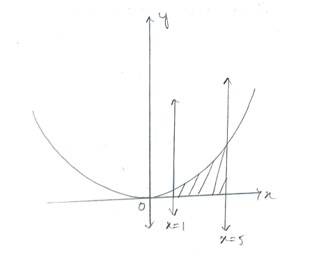
21. Find the area under the given curves and given lines:
(i) y = x2, x = 1, x = 2 and x-axis
(ii) y = x4, x = 1, x = 5 and x –axis
(i) Given of curve is and the equation are
Area enclosed
(ii) Given equation of curve is and the lines are
So, area enclosed
22. Find the area between the curves y = x and y = x2
The given equation of the curve is --------(1)
and that of the line is ---------(2)
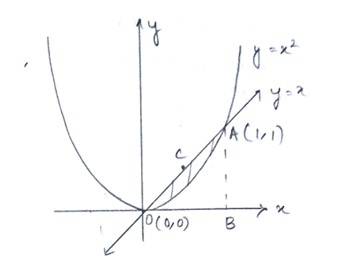
Solving eq (1) and (2)for x and y
Where,
And when
The point of intersection of the parabola and the line
Is O(0,0) and B (1,1)
Hence, area between the curve and the line is
23. Find the area of the region lying in the first quadrant and bounded by y = 4x2, x = 0, y = 1 and y = 4
Given curve is - (1)
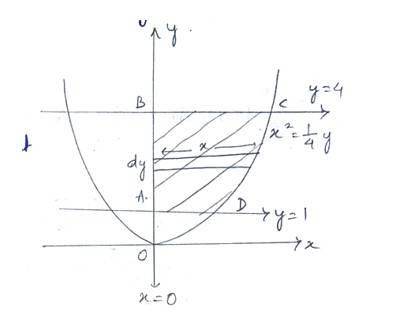
i.e, y-axis and y=4 and y=1
Hence, the required area in Ist quadrant i.e, area ABCD =
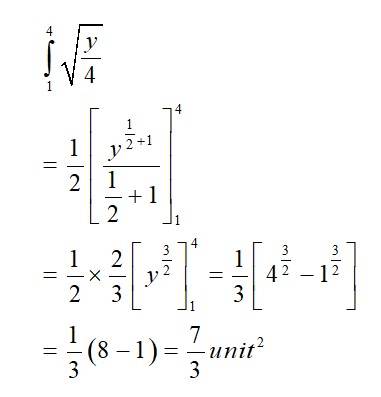
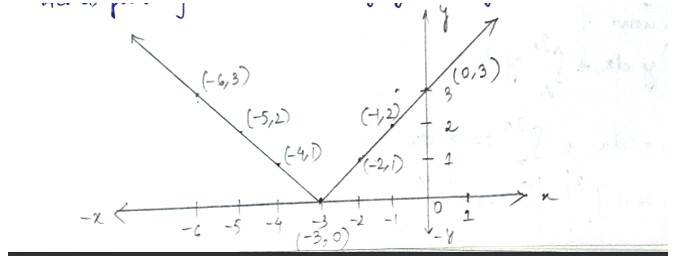
24. Sketch the graph of y = |x + 3| and evaluate
Given equation of lines is -------(1)
The point (x,y)satisfying (1)are
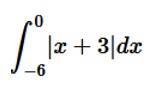

Hence plotting the above in graph we get
Now,
We know that,
So,
25. Find the area bounded by the curve y = sin x between x = 0 and x = 2π
The given equation of the curve is
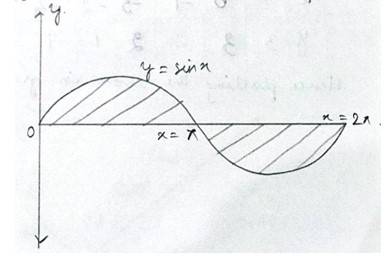
The required area bounded by the curve
26. Find the area enclosed between the parabola y2 = 4ax and the line y = mx
The equation of the parabola is -----------(1)
and that of line is ------(2)
The Point of intersection of(1)and (2) is given by
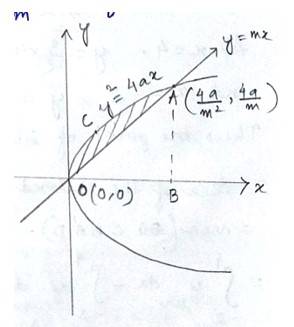
For, i.e, O(0,0)
For, (in first quadrant)
i.e,
Hence, the required area enclosed by the curve and the lines is

27. Find the area enclosed by the parabola 4y = 3x2 and the line 2y = 3x + 12
The given equation of parabola is ------------(1)
And the line is ----------------------(2)
Solving (1) and (2) for x and y,
At,
And
Thus, the point of intersection of (1)&(2)are
Area of the enclosed region (BOAB)

=area (CBAD) – area (OADC)
28. Find the area of the smaller region bounded by the ellipse 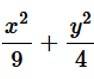 and the line
and the line 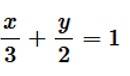
Given equation of the ellipse is Which as major axis aling x- axis and that of the line is which has x and y intercepts at 3 and 2respectively.
Required area of enclosed region is area

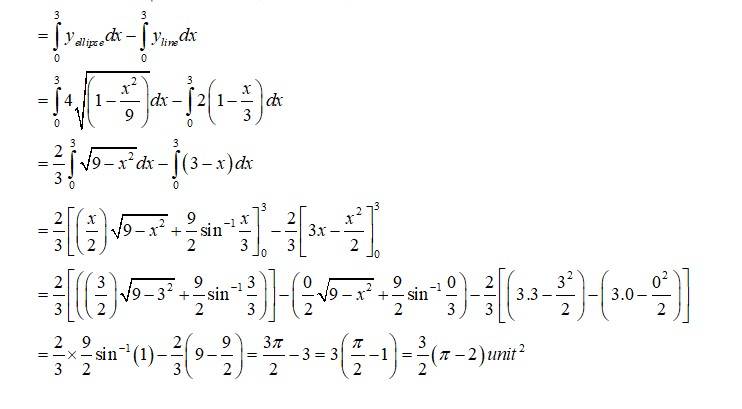
29. Find the area of the smaller region bounded by the ellipse and the line
The Given equation of the ellipse is
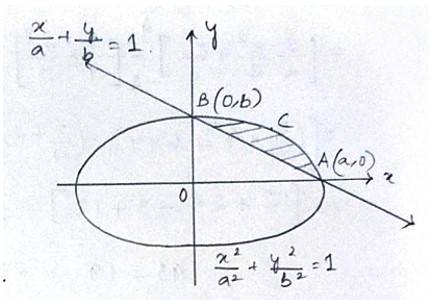
And the equation of the line in
With x and y intersept a and b
So, required area of the enclosed region is

30. Find the area of the region enclosed by the parabola x2 = y, the line y = x + 2 and x-axis
The given equation of the parabola is ---------(1)
and that the line is --------------(2)
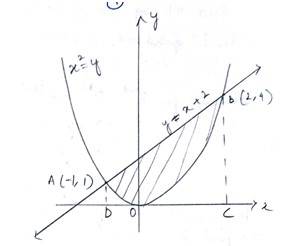
Solving (1) and (2) for x and y
When
And
The point of intersection of the parabola and the lines
Hence the required area enclosed region is
31. Using the method of integration, find the area enclosed by the curve |x| + |y| = 1
[Hint: the required region is bounded by lines x + y = 1, x – y = 1, – x + y = 1 and – x – y = 11]
Given equation of the curve is , which can be break down into each quadrant .
For Ist quadrant,
i.e., - (1)
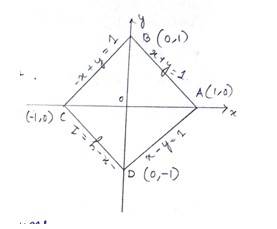
Similarly for IInd, IIIRd nad IVth quadrant
- (2)
- (3)
- (4)
We draw the above focus lines on a graph and find the area enclosed which is a square.
Required area .
32. Find the area bounded by curves {(x, y) : y ≥ x2 and y = |x|}.
Given that equation of
curve
line
Since the line passes through A&B in Ist and IInd quadrants
the equation must satisfy
for Ist quadrant and
for IInd t quadrant
So, and
and
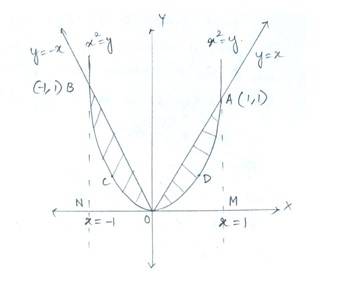
i.e, A has coordinate (1,1)
i.e, B has coordinate (1,1)
Now, area of AODA = area (AOM)-area (ADOM)
The required area of the region bounded by curve and line is
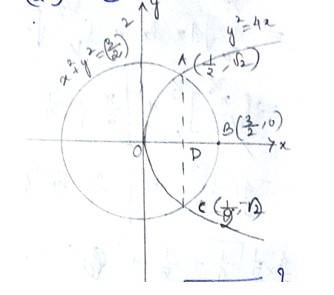
35. Find the area of the region {(x, y) : y2 ≤ 4x, 4x2 + 4y2 ≤ 9}.
The given equation of curve i.e, - (1) is a parabola and
- (2) is a circle
With centre (0,0)and radius
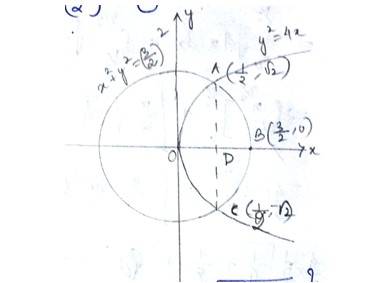
Solving (1) and (2) for x and y,

36. Choose the correct answer:
Area bounded by the curve y = x3, the x-axis and the ordinates x = –2 and x = 1 is
(A) -9
(B) -15/4
(C) 15/4
(D) 17/4
Given is and the ines
For
Total area of the bounded region
37. Choose the correct answer:
The area bounded by the curve y = x|x|, axis and the ordinates x = –1 and x = 1 is given by:
[Hint: y = x2 if x > 0 and y = –x2 if x < 0]
(A) 0
(B) 1/3
(C) 2/3
(D) 4/3
The given curve is
Which is in the form of a parabola nad the lines are
At
At
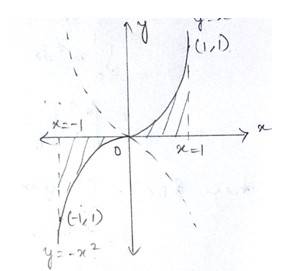
Shaded area of the Ist quadrant
Shaded area of the IInd quadrant
Total area of the enclosed region
Option (c) is correct.
38. Choose the correct answer:
The area of the circle x2 + y2 = 16 exterior to the parabola y2 = 6x is
a.
b.
c.
d.
The given area of the circle is is a circle with centre (0,0) and radius, and the parabola is -------------(2)

Solving (1) and (2) for x and y.
For,
Which is not possible.
For,
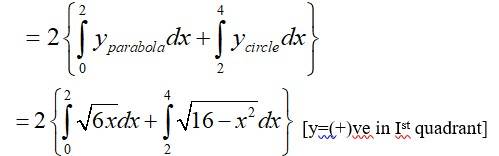

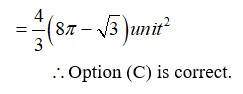
39. Choose the correct answer:
The area bounded by the y-axis, y = cos x and y = sin x when 0 ≤ x ≤ π/2.
(A) 2(√2 - 1)
(B) √2 - 1
(C) √2 + 1
(D) √2
Given curve is
for
And
We know that at i.e,
So the point of intersection is at
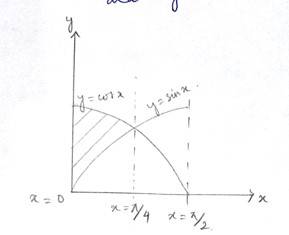

Topics Covered in NCERT Maths Class 12 Application of Integrals Chapter
- Area under Simple Curves
Maths Ncert Solutions class 12th Exam
