Solutions Class 12 Chemistry: Types of Solution, Solubility, and Important Notes

Solutions are homogeneous mixtures of two or more substances where the composition and properties are uniform throughout the mixture. 

Components of a solution

A solution is a form of two components: solvent and solute. 

Solvent is the substance present in the largest quantity that determines the physical state of the solution. Water is the most common solvent.

Solute is the substance that is dissolved in the solvent, present in smaller quantities.

For example, when you dissolve salt in water, water is the solvent and salt is the solute, which creates a saltwater solution.

Solutions can exist in all three states of matter: Gas solutions,  Liquid solutions, and Solid solutions.

Solutions are present everywhere in daily life. Your blood is a solution containing various dissolved substances, soft drinks are solutions of CO₂ and other compounds in water, and even the air you breathe is a solution of different gases. 

Properties of Solutions

• Homogeneous mixture with uniform composition throughout
• Single phase appearance regardless of number of components
• Particle size at molecular/ionic level (less than 1 nm)
• Transparent or translucent nature
• Stable without separation over time
• Do not settle under gravity
• Molecular dispersion of solute particles
• Retain chemical identity of components
• Formation is typically a physical process
• Reversible through physical separation methods

In Solutions, composition and properties remain uniform throughout. The component present in the largest quantity determines the physical state and is called the solvent, while other components are termed solutes. In binary solutions containing two components, we can classify them based on the physical states of both solute and solvent.

The formation of different solutions depends on the physical states of the components involved. The three states of matter- gas, liquid, and solid can create nine combinations of solute-solvent pairs.

Type of Solution	Solute	Solvent	Common Examples
Gaseous Solutions	Gas	Gas	Mixture of oxygen and nitrogen gases
	Liquid	Gas	Chloroform mixed with nitrogen gas
	Solid	Gas	Camphor in nitrogen gas
Liquid Solutions	Gas	Liquid	Oxygen dissolved in water
	Liquid	Liquid	Ethanol dissolved in water
	Solid	Liquid	Glucose dissolved in water
Solid Solutions	Gas	Solid	Solution of hydrogen in palladium
	Liquid	Solid	Amalgam of mercury with sodium
	Solid	Solid	Copper dissolved in gold

The concentration of a solution is the amount of solute and solvent in a solution. We can calculate the concentration of a solution in many ways, and each one is essential for scientific work and industrial applications.

Mass Percentage (w/w)

The mass of a component in the solution as a percentage of the total mass of the solution is the mass percentage. 

Mass% of a component = (Mass of the component in the solution / Total mass of the solution) × 100

Volume Percentage (V/V)

The volume of a component is to the total solution volume. It is used with liquid-liquid solutions.

Volume % of a component = (Volume of the component / Total volume of solution) × 100

Mass by Volume Percentage (w/V)

The mass of solute dissolved in 100 mL of solution. This method is used in medical and pharmaceutical applications for dosage calculation.

Parts Per Million (ppm)

When dealing with trace quantities of substances, parts per million provides a more manageable scale than percentages.

Parts per million = (Number of parts of the component × 10⁶) / Total number of parts of all components

Mole fraction

The ratio of moles of one component to the total moles of all components. It is a dimensionless quantity, valuable in thermodynamic calculations and gas mixture analysis.

Mole fraction of a component = Number of moles of the component / Total number of moles of all components

For a binary mixture with nₐ moles of component A and nᵦ moles of component B:

xₐ = nₐ/(nₐ + nᵦ)

An important property of mole fractions is that their sum always equals unity: x₁ + x₂ + … + xᵢ = 1

Molarity

The number of moles of solute dissolved in one litre of solution. This is used in analytical chemistry and laboratory preparations.

Molarity = Moles of solute / Volume of solution in litres

Molality

Molality expresses the number of moles of solute per kilogram of solvent. Unlike molarity, molality remains independent of temperature because mass doesn’t change with temperature.

Molality = Moles of solute / Mass of solvent in kg

The maximum amount of a substance that can dissolve in a specified amount of solvent at a given temperature and pressure is the Solubility. The amount dissolved depends on the nature of both solute and solvent.

The dissolution process involves a dynamic equilibrium where solute particles continuously dissolve and crystallize at equal rates. When this equilibrium is established, the solution becomes saturated, containing the maximum possible amount of dissolved solute under those conditions.

Solute + Solvent ⇌ Solution

Solubility of a Solid in a Liquid

The amount of solid that can be dissolved in liquids depends on temperature and follows Le Chatelier’s principle. 

Le Chatelier’s principles state that at a dynamic equilibrium, when a reaction undergoes a change in concentration, temperature, or pressure, it will counteract that and adjust itself to maintain the equilibrium.

For endothermic dissolution processes (ΔsolH > 0), solubility increases with an increase in temperature. And for exothermic processes (ΔsolH < 0), solubility decreases as temperature increases.

Pressure has minimal effect on solid-liquid solubility because both phases are highly incompressible.

Solubility of a Gas in a Liquid

The solubility of a gas in a liquid depends on pressure and temperature. By increasing the pressure, the solubility of the gas increases by forcing more gas molecules into the liquid phase.  Higher temperature decreases gas solubility.

Henry Law

Henry’s Law states that at constant temperature, the solubility of a gas in a liquid is directly proportional to the partial pressure of the gas above the solution surface.

p = KH × x

Where,

• p is the partial pressure of the gas
• KH is Henry’s law constant
• x is the mole fraction of gas in solution.

Higher KH values mean lower gas solubility. The increase in KH values with temperature for N₂ and O₂ confirms that gas solubility decreases with increasing temperature.

Applications of Henry’s Law

• Soft drinks are bottled under high CO₂ pressure to increase gas solubility. 
• Scuba divers must manage high concentrations of dissolved nitrogen in their blood under pressure, and the condition known as “bends” occurs when rapid pressure reduction causes nitrogen bubbles to form in blood vessels.

The vapour pressure of liquid solutions depends on the volatility of their components. Volatile components add up to the total vapor pressure as per their concentration and individual characteristics.

Vapour Pressure of Liquid-Liquid Solutions

The two volatile liquids of a binary solution contribute to the total vapor pressure. Raoult’s Law establishes the quantitative relationship between partial vapor pressures and mole fractions.

Raoult’s Law

Raoult’s law states that for a solution of volatile liquids, the partial vapor pressure of each component is directly proportional to its mole fraction in the solution.

p₁ = p₁⁰ × x₁

p₂ = p₂⁰ × x₂

Where,

• p₁⁰ and p₂⁰ = vapor pressures of pure components
• x₁ and x₂ are their mole fractions.

The total vapor pressure follows Dalton’s law:

ptotal = p₁ + p₂ = x₁p₁⁰ + x₂p₂⁰

Or, ptotal = p₁⁰ + (p₂⁰ - p₁⁰)x₂

This linear relationship permits the calculation of total vapour pressure from the composition of any binary volatile solution.

Raoult’s Law as a special case of Henry’s Law

If you compare Raoult's law (p = x × p⁰) with Henry's law (p = KH × x), you will notice that both exhibit direct proportionality between mole fraction and partial pressure. Raoult's law becomes a special case of Henry's law when KH is equal to p⁰, the vapor pressure of the pure substance.

Ideal solutions obey Raoult’s law over the entire concentration range and show two additional characteristics, zero enthalpy of mixing (ΔmixH = 0) and zero volume of mixing (ΔmixV = 0).

These characteristics occur when intermolecular forces between different components (A-B interactions) are nearly equal to those between like molecules (A-A and B-B interactions). No heat is absorbed or evolved during mixing, and the solution volume equals the sum of component volumes.

Examples of ideal solutions: bromoethane and chloroethane, and benzene and toluene. 

Non-ideal Solutions

Non-ideal solutions oppose Raoult’s law, showing only one positive or negative deviation based on the strength of intermolecular interactions.

When A-B interactions are weaker than A-A or B-B interactions, positive deviation occurs, resulting in easier escape of molecules than in pure states, and an increase in vapor pressure than the ideal value. 

Negative deviation results when A-B interactions are stronger than A-A and B-B interactions, reducing the capabilities for molecules to escape and lowering vapor pressure below ideal values. 

Colligative properties depend on the number of solute particles present, regardless of their chemical identity. These properties are used for determining molar masses and understanding solution behavior.

Relative Lowering of Vapour Pressure

The vapor pressure of a solution is always lower than that of the pure solvent when a non-volatile solute is present. The relative lowering of vapor pressure equals the mole fraction of the solute.

Δp₁/p₁⁰ = x₂ = n₂/(n₁ + n₂)

For dilute solutions where n₂ << n₁:

Δp₁/p₁⁰ = n₂/n₁ = (w₂ × M₁)/(M₂ × w₁)

This relationship allows calculation of molar mass M₂ when other quantities are known.

Elevation of Boiling Point

The boiling point of solutions is higher than pure solvents because of reduced vapor pressure, which requires additional heating to reach atmospheric pressure. The boiling point elevation is directly proportional to molal concentration.

ΔTb = Kb × m

Where,

Kb is the boiling point elevation constant specific to each solvent.

For calculating molar mass:

M₂ = (Kb × w₂ × 1000)/(ΔTb × w₁)

Depression of Freezing Point

The freezing point of solutions is lower than pure solvents because the equilibrium between solid and liquid phases shifts to lower temperatures. The freezing point depression is proportional to molal concentration.

ΔTf = Kf × m

Where Kf is the freezing point depression constant (cryoscopic constant).

For molar mass determination:

M₂ = (Kf × w₂ × 1000)/(ΔTf × w₁)

The constants Kf and Kb can be calculated from fundamental thermodynamic properties:

Kf = (R × M₁ × Tf²)/(1000 × ΔfusH)

Kb = (R × M₁ × Tb²)/(1000 × ΔvapH)

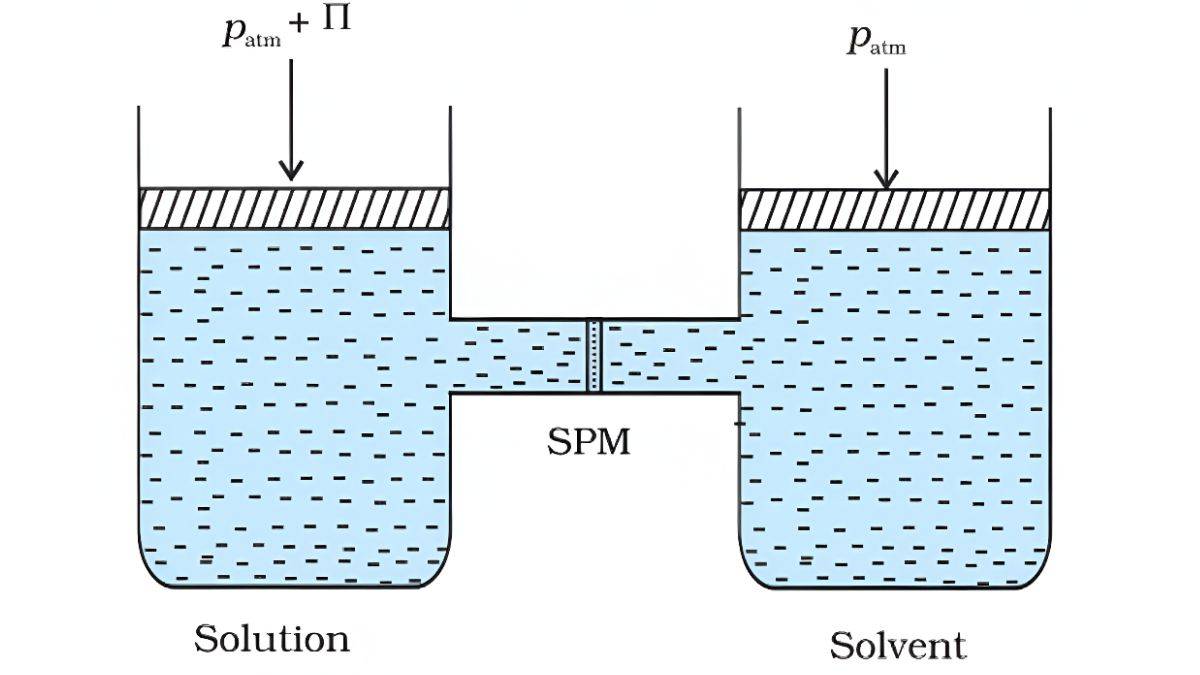
Osmosis and Osmotic Pressure

The process in which solvent molecules flow through semipermeable membranes from pure solvent to solution is called Osmosis. 

The pressure required to prevent this flow is called osmotic pressure.

π = CRT = (n₂/V)RT

For molar mass determination:

M₂ = (w₂RT)/(πV)

Reverse osmosis occurs when pressure higher than the osmotic pressure is applied to solutions, forcing solvent molecules to flow in the opposite direction. This process enables seawater desalination for producing potable water.

Read More: Colligative Properties and Molar Mass