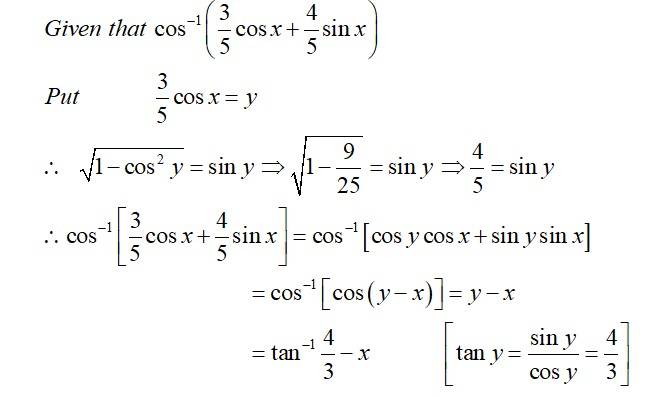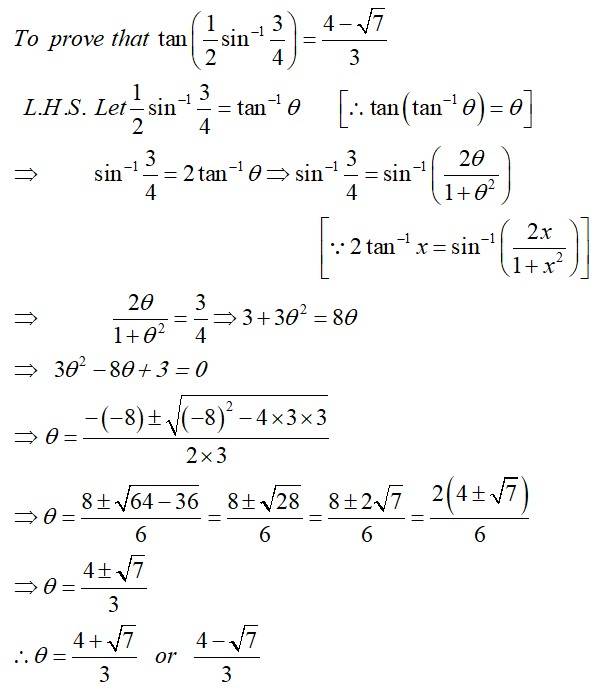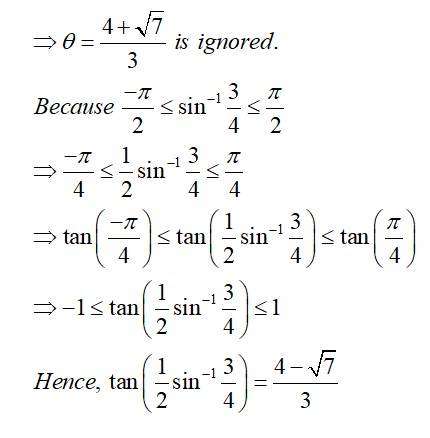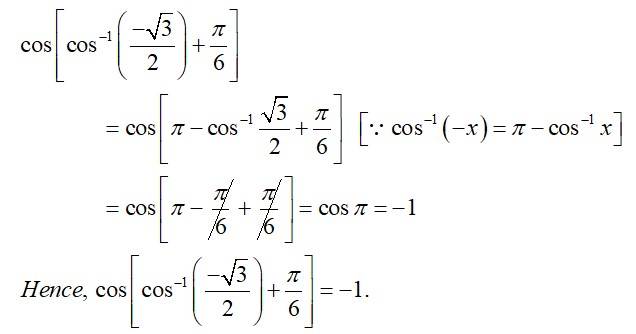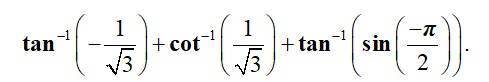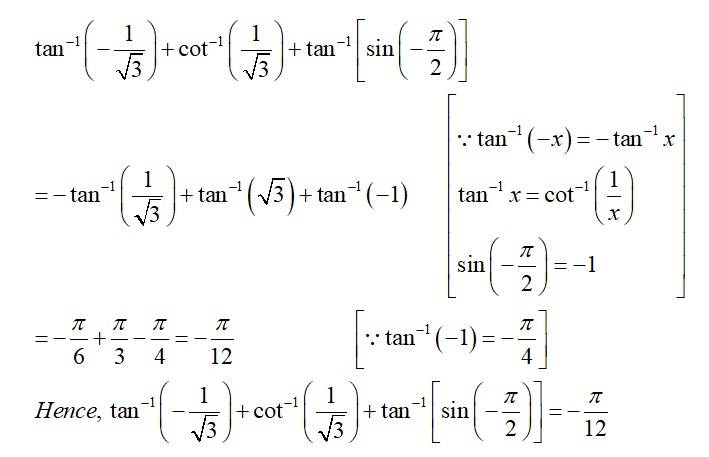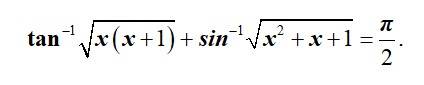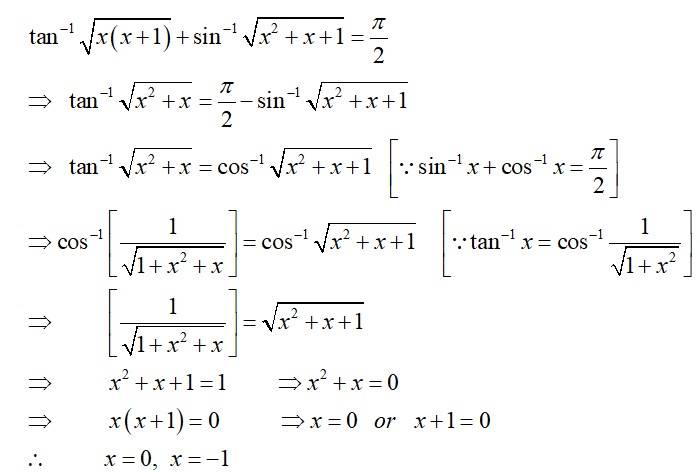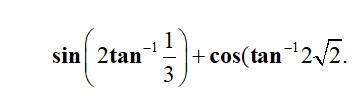Table of contents
- Inverse Trigonometric Functions Long Answers Type Questions
- Inverse Trigonometric Functions More Long Answers Type Questions
- Inverse Trigonometric Functions Short Answers Type Questions
Inverse Trigonometric Functions Long Answers Type Questions
Q1. 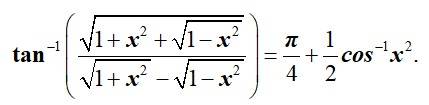 |
| Sol. |
| Q2. Find the simplified form of |
| Sol. |
| Q3. Prove that |
| Sol. |
| Q4. Show that |
| Sol. |
Inverse Trigonometric Functions More Long Answers Type Questions
Q5. Prove that 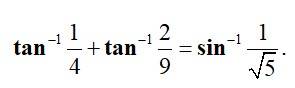 |
| Q6. Find the value of |
| Sol.
|
Q7. Show that  and justify why the other value and justify why the other value  is ignored? is ignored?
|
| Sol. |
| Q8. If is an arithmetic progression with common difference , then evaluate the following expression: tan[ |
| Sol. |
Inverse Trigonometric Functions Short Answers Type Questions
| Q1. Find the value of |
| Sol:
|
Q2. Evaluate  |
| Sol. |
| Q3. Prove that 7 |
| Sol:
|
| Q4. Find the value of |
| Sol. |
| Q5. Find the value of |
| Sol:
|
| Q6. Show that |
| Sol:
|
| Q7. Find the real solutions of the equation |
| Sol: |
| Q8. Find the value of the expressions |
| Sol. |
| Q9. If , then show that . where n is any integer. |
| Sol:
|
| Q10. Show that |
| Sol.
|
| Q11. Solve the following equation: |
| Sol: |
Maths NCERT Exemplar Solutions Class 12th Chapter Two Exam
Student Forum
Other Similar chapters for you
News & Updates
Latest NewsPopular News