Application of Gauss's Law: Class 12 Physics

These are the approaches to understanding different symmetries and calculating electrostatic field problems when Gauss' Law applies, and to replacing complex, nearly impossible integrations. 

You’ll need to conceptually and mathematically master these three applications of Gauss' Law, which are asked in CBSE and competitive exams. 

1. Electric Field of a Uniformly Charged Straight Wire
2. Electric Field Near a Uniformly Charged Infinite Sheet
3. Electric Field of a Uniformly Charged Thin Spherical Shell

These Gauss’ Law applications in Class 12 Electrostatics will also need your previous knowledge of four central concepts. 

• Electric Field Lines - These are imaginary curves created when there are positive and negative charges present. 
• Electric Flux - This describes how electric field lines behave when passing through an electric field. 
• Continuous Charge Distribution - Charge distributions are of different types in physics, where they can be described as along a line, on a surface, or in a volume.
• Gauss’ Law - Applying only to closed surfaces, the total electric flux equals the total electric charge that’s inside divided by the permittivity of free space.  

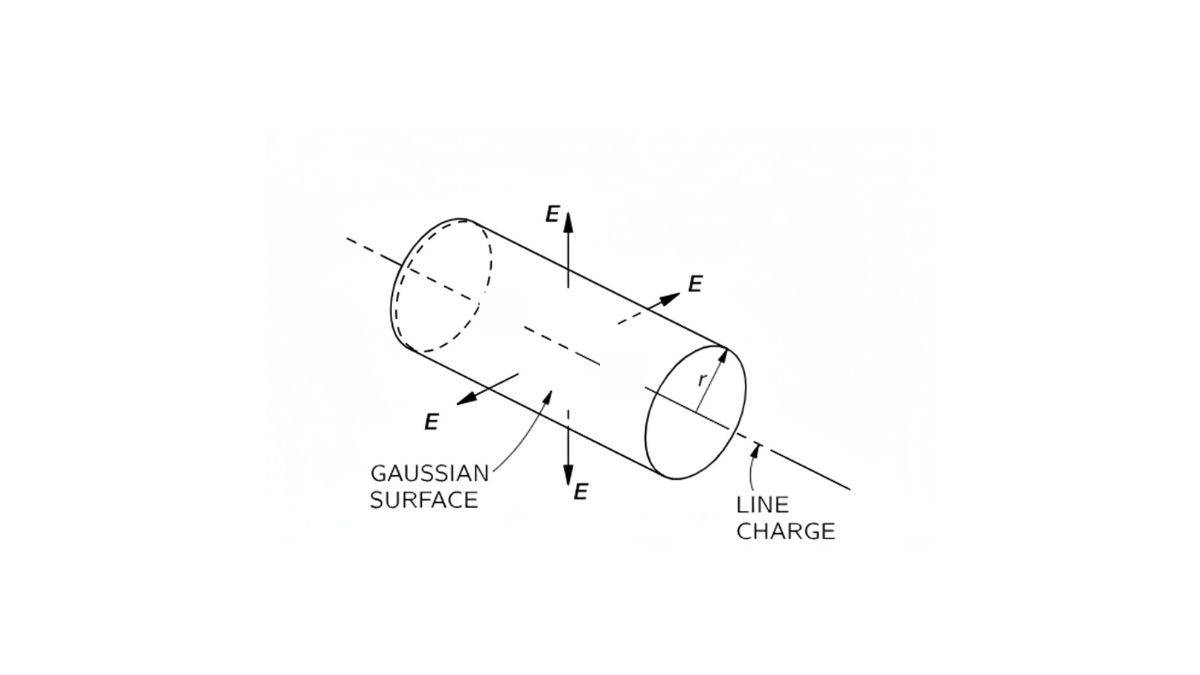
This is a simple application of Gauss’s Law. The scenario here is a long, thin wire carrying an electric charge that extends indefinitely.
Since it is a straight wire, we can think of it as having a linear charge density, λ. 

How are we going to find the electric field in this case?
We will have to assume a few things and apply what we learnt from earlier in the chapter.

• The electric field will point straight and outwards from the wire. The reason is that the opposite sides will be cancelling any sideways effects. 
• The strength of the field can be assumed to be equal at all points with the same distance from the wire. 
• The radial pattern and uniform strength will be achieved only when the wire is symmetrical.

After these considerations, we’ll apply Gauss' Law by thinking there is a Gaussian surface surrounding this wire. And if you remember, this surface is a construct.
So we will consider this surface to be a cylinder with a common axis along the line. See the below figure.

By Gauss’ Law definition, we have the electric flux through the curved part of the cylinder. That flux is equal to the charge enclosed within it, and we divide that charge by ε_0. 

And when we read of flux meaning in this law, we learnt that the field is perpendicular, ie, normal to the curved surface of the cylinder.
The total electric flux is E x 2πr (remember that flux Φ = E x A, and the area is two times the radius and the length is 1 unit for the sake of simplicity).
The stepwise calculation of the electric field of a uniformly charged straight wire using Gauss’ Law would be like:

• Linear charge density is λ = Q/L or λ = q/l, so charge is q = λl
• Surface area of the Gaussian cylinder is 2πrl or simply 2πr
• Using the algebraic form of Gauss' Law equation Φ = q_enc/ε_0
• Substituting all values in this equation
  

Ex 2πrl = λl/ε_0

The total electric field then

E = λl/2πrlε_0

Or,

E = λ/2πrε_0

This application of Gauss’ Law with a uniform charged wire tells us:

The electric field will become weaker the farther you move from the wire.
This concept is used in electronic transmissions in the real world. 

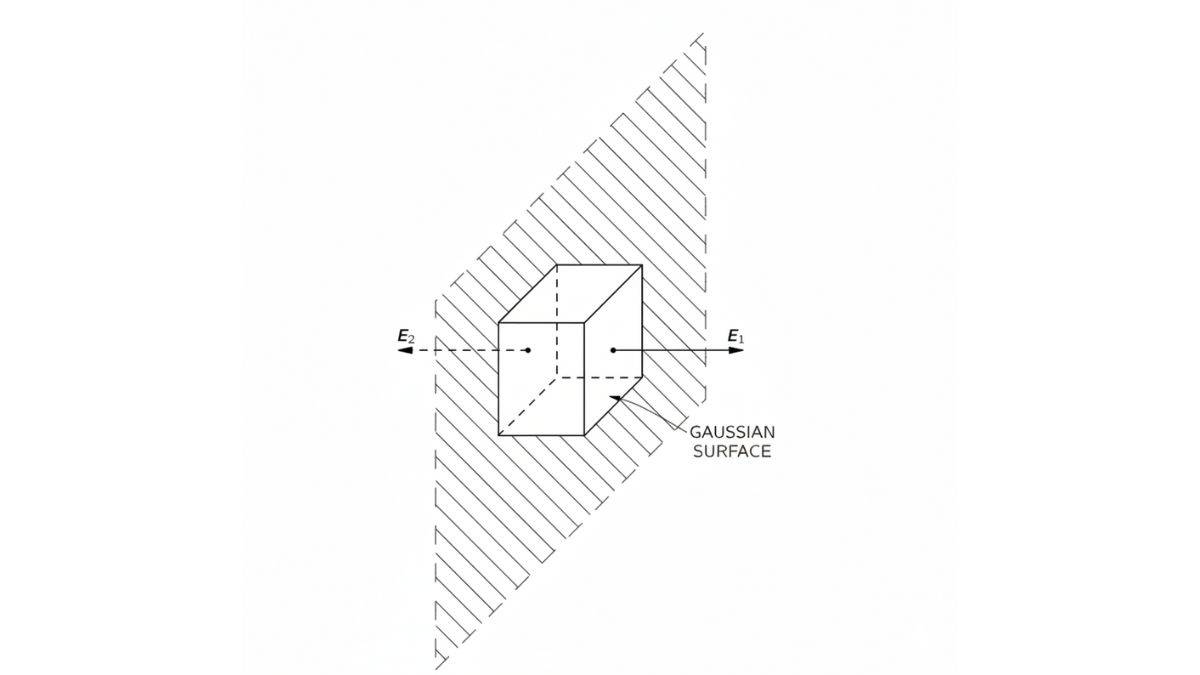
Now comes another application of Gauss’s Law. That is, instead of the wire, we have a uniformly charged sheet. What would the electric field calculation look like?
Here, we just assume the electric field lines are outward and perpendicular to the sheet's surface.
And since we are considering that it’s a surface that keeps extending to infinity. We need to look at the charge per unit area. For that, we’d be using the surface charge density expression, which is σ = q/A or σ = q/s (as we use area as A or s).

Now, we move on to consider a closed surface as the Gaussian Law dictates. This surface comes from creating a rectangular box or Gaussian surface that passes through the sheet in parallel. See the figure below. 

There are parallel surfaces, where each will have the same area and the electric field will be perpendicular to the two parallel faces. The ones along the sheet will have no flux.

Calculating the electric field when it’s near a uniformly charged infinite sheet:

• Finding the Gaussian surface total, we have two, that is, E_1A and E_2A. 
• Summing these up, we get 2EA for the total electric flux, Φ.
  Φ = 2EA
• We know the surface charge density in this case, σ = q/A, so charge q = σA
  
• Substitute everything into the Gauss law equation, Φ = q_enc/ε_0, to
  
  

2EA = σA/ε_0

Then,

E = σA/2Aε_0

Or, 

E = σ/2ε_0

What is this derivation telling us?
The electric field from an infinitely charged sheet is dependent only on the surface charge density. It’s not dependent on the distance (how far or close it is) from the sheet. 

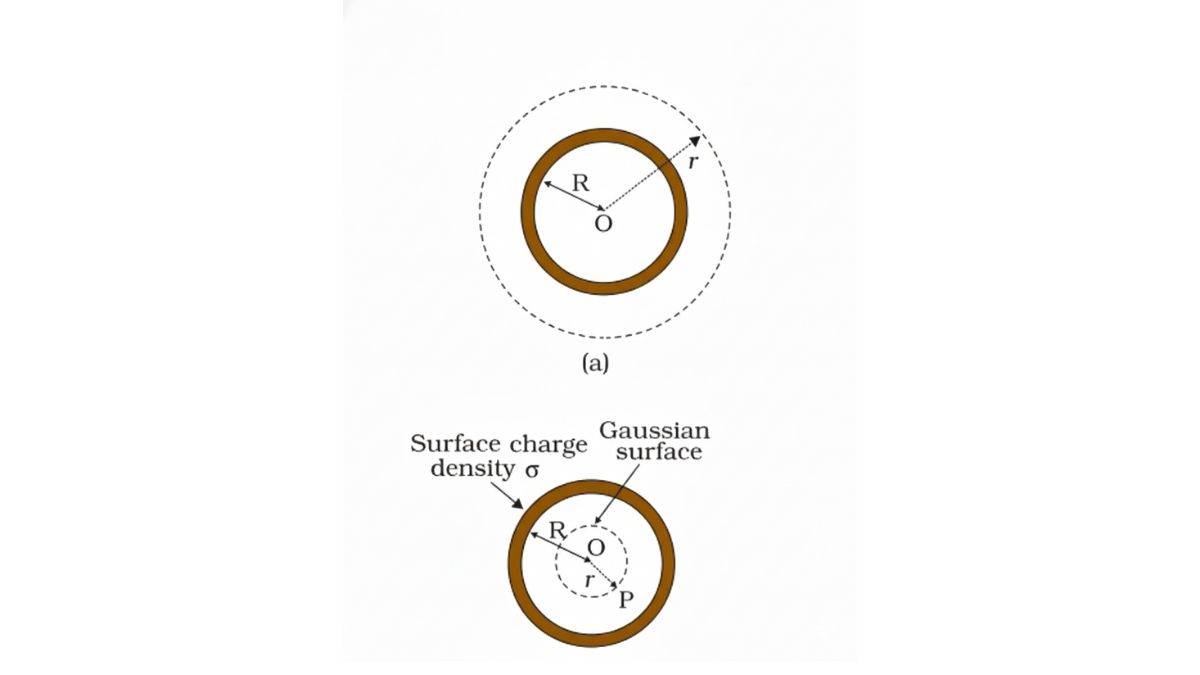
The uniformly charged shell is symmetrical, which gives us one of the most interesting applications of Gauss’s Law.
We can do electric-field calculations inside and outside the shell, a case we haven’t touched upon so far. 

Two assumptions are essential when considering a symmetrical sphere with a uniform charge:

• One is that the electric field is radial.
• Second, this field will be equal in magnitude at any point at an equal distance from the centre. 

You can see this image for reference, recreated from NCERT.  

Electric Field Outside the Shell

When the electric field is outside the shell, the electric field concentrates at the centre.
To consider a Gaussian sphere of radius r> R, is to think of a sphere, ie, the Gaussian surface, which has the same centre on the same point as the spherical shell. Just know that its radius r is larger than the shell’s radius, R. 

Using the same Gauss Law equation

Φ = q_enc/ε_0

Now since the surface area is the sphere, we have the formula as 4πr^2.

So, when equating Φ = EA, we have total electric flux as

 

Φ = E x 4πr^2

Substituting that into the Gauss Law equation, we have

E x 4πr^2 = q_enc/ε_0

E = q_enc/4πr^2ε_0

Electric Field Inside the Shell

There would be no electric field inside the shell, and then E = 0. 

That means all electric field lines cancel out. 

What can we gather from here?
The shell acts as a point charge at its centre, when we are calculating the charge outside the shell. Inside the shell, the field is zero. 

• For a uniformly charged straight wire, electric field is
  E = λ/2πrε_0
• If it’s an indefinite sheet with uniform electric charge, electric field is
  E = = σ/2ε_0
• When it is a uniformly charged spherical shell, the electric field only exists outside the shell, and the formula is 

E = q_enc/4πr^2ε_0

Chances are, you want to learn more and ace your class 12 exams and prepare for the upcoming competitive tests. Find all fresh study material, updated regularly and aligning with the recent NCERT syllabus.