
Class 12 Continuity and Differentiability introduces concepts of continuity, differentiability and relations between them. It also covers the differentiation of inverse trigonometric functions, exponential, and logarithmic functions. It also includes the Logarithmic Differentiation, Exponential and Logarithmic Functions, and Derivatives of Functions in Parametric Forms.
Continuity and Differentiability Class 12 is an important chapter of Class 12 Maths. It introduces some fundamental theorems related to the topic and the exponential and logarithmic functions which lead to powerful techniques of differentiation. Students preparing for the Class 12 CBSE Board exams and other entrance exams like JEE Main can prepare from this solution.
Shiksha offers NCERT solutions of all chapters of Physics, Chemistry and Maths of Class 11 and Class 12. These solutions are created by the subject matter experts. Students also get the key topics and free PDFs for each chapter.
- Key Concepts of Continuity and Differentiability – Class 12 Guide
- Class 12 Chapter 5 Maths Solutions – Continuity and Differentiability PDF
- Class 12 Continuity and Differentiability : Key Topics, Weightage
- Continuity and Differentiability Class 12 Maths Important Formulas
- Class 12 Math Continuity and Differentiability Exercise-wise Solutions
- Class 12 Math Continuity and Differentiability Exercise 5.1 Solutions
Key Concepts of Continuity and Differentiability – Class 12 Guide
Here are a few highlights of the Continuity and Differentiability Class 12 NCERT Solutions:
- Continuity and Differentiability states that a real-valued function at a point is called continuous if at that point the limit of the function equals the value of the function. If a function is continuous on the whole of its domain, then it is a continuous function.
- The addition, difference, product and quotient of continuous functions are continuous. If f and g are continuous functions then -
- These are some of the standard derivatives (in appropriate domains):
To get a comprehensive NCERT Solutions for Class 12 Maths with free PDFs and important topics, explore - Class 12 Maths NCERT Solutions.
Class 12 Chapter 5 Maths Solutions – Continuity and Differentiability PDF
Students can download the Continuity and Differentiability Class 12 Solutions PDF from the link given here. The PDF provides detailed and ideal study material for exam preparation. By preparing from the PDF, students can get a high score in the CBSE Board exam and competitive exams like JEE Main.
Class 12 Math Chapter 5 Continuity and Differentiability Solution: FREE PDF Download
More Useful Links
| NCERT Notes for Class 11 & 12 | NCERT Class 12 Notes | Class 12 Maths Notes PDF |
Class 12 Continuity and Differentiability : Key Topics, Weightage
Class 12 Continuity and Differentiability is also important for the JEE Main entrance test, as the chapter is a foundational topic for the larger calculus section. Here are the topics covered in this chapter:
| Exercise | Topics Covered |
|---|---|
| 5.1 | Introduction |
| 5.2 | Continuity |
| 5.3 | Differentiability |
| 5.4 | Exponential and Logarithmic Functions |
| 5.5 | Logarithmic Differentiation |
| 5.6 | Derivatives of Functions in Parametric Forms |
| 5.7 | Second Order Derivative |
Continuity and Differentiability Class 12 Weightage in JEE Mains
| Exam | Number of Questions | Weightage |
|---|---|---|
| JEE Main | 3 questions | 10% |
Continuity and Differentiability Class 12 Maths Important Formulas
Continuity and Differentiability Important Formulae for CBSE and Competitive Exams
Students can check the basic formulae used in the Continuity and Differentiability class 12 solutions. check below;
-
Basic Derivatives
-
Inverse Trigonometric Functions
-
Product Rule
-
Quotient Rule
-
Chain Rule
-
Logarithmic Differentiation
For -
Mean Value Theorem
Class 12 Math Continuity and Differentiability Exercise-wise Solutions
Chapter 5 Continuity and Differentiability deals with concepts of continuity, differentiability, and their applications. Continuity and Differentiability play a critical part in calculus, as a building block of the foundation for advanced topics like integration and differential equations. The exercise-wise Continuity and Differentiability NCERT solutions will help students understand all concepts with their examples. These solutions will help them develop problem-solving skill related to continuity at a point, derivatives, logarithmic differentiation, and the application of theorems like Rolle’s and Lagrange’s Mean Value Theorem. Students can check the exercise-wise solutions for Continuity and Differentiability below;
Class 12 Math Continuity and Differentiability Exercise 5.1 Solutions
Class 12 Continuity and Differentiability Exercise 5.1 focuses on fundamental concepts important to building a strong foundation. Exercise 5.1 deals with topics such as continuity at a point, differentiability, and application of differentiability-related formulas. Class 12 Math Exercise 5.1 Solutions includes 34 Questions (Short Answers Type) with conceptual explanation. students can check the complete solutions for exercise 5.1 below;
Exercise – 5.1
| Q1.Prove that the function f(x) = 5x 3f is continuous at x = 0, at x = – 3 and at x = 5. |
| A.1.Given, f(x) = 5x 3 At x = 0, 5x 3 = 5 0 3 = 3. So f is continuous at x = 1. At x = 3, 5x 3 = 5 ( 3) 3 = 15 3 = 18. So f is continuous at x = 3. At x = 5, .5x 3 = 5.5 3 = 25 3 = 22. So, f is continuous at x = 5. |
| Q2.Examine the continuity of the function f(x) = 2x2 1 |
| A.2. Given, f(x) = 2x2 1 At x = 3 Lim f(x) = 2(3)2 1 = 18 1 = 17. So, f is continuous at x = 3. Q3.Examine the following functions for continuity.
|
| Q3. Examine the following functions for continuity. |
| A.3. (a) Given, f (x) = x 5. The given f x n is a polynernial f xn and as every pohyouraial f xn is continuous in its domain R we conclude that f (x) is continuous. (b). Given, f(x) = For any a {5},
and f(a) = i e, f(x) = f(a). Hence f is continuous in its domain. (c) Given, f(x) = For any a { 5} = a 5 And f(a) = = a 5 f(x) = f(a). So, f is continuous in its domain. (d) Given f (a) = For x = c < 5. f (c) = (c 5) = 5 c. f(x) = (x 5) = (c 5) = 5 c. ∴ f(c) = f(x). So f is continuous. For x = c > 5. f (c) = (x 5) = c 5 f(x) = (x 5) = c 5. ∴ f(c) = f(x) So, f is continuous. For x = c = 5, f (5) = 5 5 = 0 f(a) = (x 5) = (5 5) = 0 f(x) = (x 5) = 5 5 = 0 ∴ + (x) = + (x) = f (c) Hence f is continuous. |
| Q4. Prove that the function continuous at where n is a positive integer. |
| A.4.Given, f(x) = x n > n = positive. At x = 2, (x) = n n. f(x) = x n = n n ∴ f(x) = f(x) So f is continuous at x = n. |
Commonly asked questions
20. Discuss the continuity of the following functions:
20. (a) Given f(x) = sin x + cos x
(b). Given, f(x) = sin x cos x
(c). Given, f(x) = sin x .cos x.
Let g(x) = sin x and h(x) = cos x.
If g or h are continuous f x then
g + h
g h
g h are also continuous.
As g(x) = sin x is defined for all real number x.
Let , and putting x = c + h. we see that as
Then g(c) = sin c
g(x) = sin x = sin (c + h).
= (sin c cos h + cos c sin h )
= sin c. cos 0 + cos c. sin 0
= sin c 1 + 0
= sin c
= g (c)
So, g is continuous x R.
And h (c) = cos c
= g(x) = sin x = cos (c + h)
= cos c .cos 0 sin c. sin 0
= cos c .1 0.
= cos c = h(c).
As g and h are continuous x R.
The f x f(x)
3. Examine the following functions for continuity.
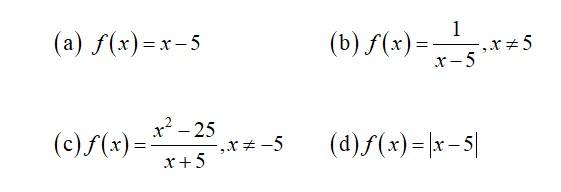
3. (a) Given, f (x) = x 5.
The given f x n is a polynernial f xn and as every pohyouraial f xn is continuous in its domain R we conclude that f (x) is continuous.
(b). Given, f(x) =
For any a {5},
and f(a) =
i e, f(x) = f(a).
Hence f is continuous in its domain.
(c) Given, f(x) =
For any a { 5}
= a 5
And f(a) =
= a 5
f(x) = f(a).
So, f is continuous in its domain.
(d) Given f (a) =
For x = c < 5.
f (c) = (c 5) = 5 c.
f(x) = (x 5) = (c 5) = 5 c.
∴ f(c) = f(x).
So f is continuous.
For x = c > 5.
f (c) = (x 5) = c 5
f(x) = (x 5) = c 5.
∴ f(c) = f(x)
So, f is continuous.
For x = c = 5,
f (5) = 5 5 = 0
f(a) = (x 5) = (5 5) = 0
f(x) = (x 5) = 5 5 = 0
∴ + (x) = + (x) = f (c)
Hence f is continuous.
22. Find all points of discontinuity of , where
22. Given f(x) =
For x = c < 0,
f(c) =
f(x) =
So, f is continuous for x < 0
For x = c > 0
f(c) = c + 1
f(x) = x + 1 = c + 1 = f(c)
So, f is continuous for x > 0.
For x = 0.
L.H.L. =
R.H.S. =
And f(0) = 0 + 1 = 1
L.H.L = R.H.L. = f(0)
So, f is continuous at x = 1.
Hence, discontinuous point of x does not exit.
59. Kindly consider the following
59. Let y =
77. Kindly consider the following
77. Let y = x sin x + (sin x) cos x
Putting u = x sin x and v = (sin x) cos x we have,
y = u + v
_____ (1)
As u = x sin x
Taking log,
Log u = sin x log x
Differentiating w r t ‘x’,
,
= sin x log x + log x sin x
= + cos x log x
= x sin x
And v = (sin x) cos x
Taking log,
Log v = cos x log (sin x).
Differentiating w r t ‘x’,
= cos x log (sin x) + log (sin x) cos x
sin x- sin x log (sin x)
= cot x cos x- sin x log (sin x)
= v [cot x cos x - sin x log (sin x)]
= (sin x) cos x [cot x cos x- sin x log (sin x)]
Hence, eqn (1) becomes
+ (sin x) cos x [cot x cos x- sin x log (sin x)]

Differentiating w r t. ‘t’ we get,
So,
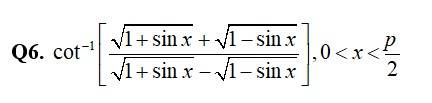

(i) by product rule
3x4 + 7x2- 15x3- 35x + 24x2 + 56 + 2x4- 5x3 + 14x2- 35x 18x-45
= 5x4- 20x3 + 45x2- 52x + 11
(ii)
Taking log in eqn (1)
Now, Differe(iii) ntiating w r t ‘x’ we get,
2x4 + 14x4 + 18x- 35x- 45 + 3x1- 15x3 + 24x2 + 7x2- 35x + 56]
= 5x4- 20x3 + 45x2- 52x + 11
We observed that all the methods give the same result.
5. Is the function defined by
Find all points of discontinuity of , where is defined by
5. Given, f (a) =
At x = 0,
(0) = 0
f (x) = x = 0
∴ f (x) = f (0)
So, f is continuous at x = 0.
At x = 1,
Left hand limit,
L.H.L = f (x) = x = 1.
Right hand limit,
R. H. L. = f (x) = 5 = 5.
L.H.L. R.H.L.
So, f is not continuous at x = 1.
At x = 2,
f (2) = 5.
f (x) = 5 = 5
(x) = f (2)
So f is continuous at x = 2.
Find all points of discontinuity of f, where f is defined by
43. Prove that the greatest integer function defined by
is not differentiable at = 1 and = 2.
43. The given f x n is
f(x) = 0 < < 3
At x = 1
L×H×L× =
Hence lines does not exist
Qf is not differentiable at x = 1
At x = 2
L×H×L =
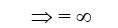
Hence, limit does not exist.
Qf is not differentiable at x = 2
23. Determine if defined by
is a continuous function?
23. Given f (x) =
For x = c 0,
f (c) =
So, f is continuous for
For x = 0,
f (0) = 0
As we have sin
f (x) = 02 a where
= 0 = f (0).
∴ f is also continuous at x = 0.
84. Find the derivative of the function given by and hence f'(1)
84. Given, f(x) = (1 + x)(1 + x 4)(1 + x 8)
Taking log,
logf(x) = log (1 + x) + log (1 + x) + log (1 + x 4) + log (1 + x 8)
Now, Differentiating w r t ‘x’ we get,
Putting x = 1
f`(x) = (1 +1)(1 + 14)(1 +18)
52.Kindly consider the following
52. Kindly go through the solution

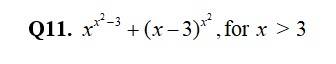
Putting we get,
________(1)
Now,
Taking log,
And
Hence eqn (1) becomes
64. Kindly consider the following
64. Let y = ex + ex2 + … + ex5.
(ex + ex2 + ex3 + ex4 + ex5).
= ex + 2x ex2 + 3x2ex3 + 4x3ex4 + 5eex4


18. Show that the function defined by is discontinuous at all integral
points. Here denotes the greatest integer less than or equal to .
18. Given, g (x) = x [x].
For
g (n) = n [n] = nn = 0
f (x) = (x [x]) = n [n 1] = n + 1 = 1
g (x) = x [x] = n [n] = 0
So, g (x) g (x).
g (x) is d is continuous at all x
7.
7. Given, f(x) =
For x =
f ( 3) = e + 3 (∴x< 3, )
f(x) =
∴ f(x) = f(c)
So, f is continuous at x = c < 3.
For x = c > 3
f(3) = 6.3 + 2 = 18 + 2 = 20
f(x) = 6x + 2 = 18 + 2 = 20
∴ f(x) = f(c).So f is continuous at x = c > 3.
For. C = 3,
f ( 3) = ( 3) + 3 = 6.
f(x) = .x + 3 = ( 3) + 3 = 6.
f(x) = ( 2x) = 2 ( 3) = 6.
∴ f(x) = f(x) = f( 3)
So, f is continuous at x = c = 3.
For c = 3,
f(3) = 6.3 + 2 = 18 + = 20.
f(x) = 2x = 2 (3) = 6
f(x) = (6x + 2) = 6.3 + 2 = 20
∴ f(x) f(x).
f is not continuous at x = 3 point of discontinuity
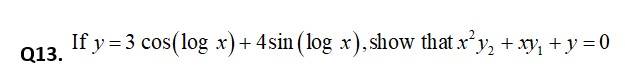
So,
______________(1)
Differentiating eqn (1) w r t ‘x’ we get,
9.
9. Given, f (x) =
For x = c < 1,
f (x) = x2 + 1 = c2 + 1
∴ f (x) = f (c)
So f is continuous at x = c < 1.
For x = c > 1,
F (c) = c + 1
f (x) = x + 1 = c + 1
∴ f (x) = f (c)
So, f is continuous at x = c > 1.
For x = c = 1, + (1) = 1 + 1 = 2
L.H.L. = f (x) = x2 + 1 = 12 + 1 = 2.
R.H.L. = f (x) = x + 1 = .1 + 1 = 2
∴ L.H.L = R.H.L. = f (1)
So, f is continuous at x = 1.Hence f has no point of discontinuity.
40. Kindly consider the following

40. Kindly go through the solution
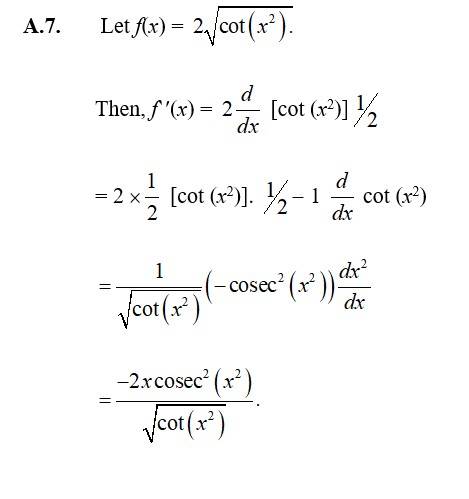
48. Kindly consider the following
48. Given, x2 + xy + y2 = 100.
Differentiating w r t ‘x’ we get,
47. Kindly consider the following
47. Given, xy + y2 = tan x + y Differentiating w r t x we get,
6.
6. Given f(x) =
For x = c < 2,
F (c) = 2c + 3
f(x) = 2x + 3 = 2c + 3
∴ f (x) = f(c)
So f is continuous at x 2.
For x = c > 2.
F (c) = 2c 3
f(x) = 2x 3 = 2c 3
∴ f(x) = f(c)
So f is continuous at x 2.
For x = c = 2,
L.H.L. = f(x) = .2x + 3 = 2. 2 + 3 = 4 + 3 = 7.
R.H.L. = f(x) = 2x 3 = 2. 2 3 = 4 3 = 1.
∴ LHL RHL
∴ f is not continuous at x = 2.i e, point of discontinuity
81. Kindly consider the following
81. Given, yx = xy
Taking log,
x log y .log x
Differentiating w r t ‘x’ we get,
119. Kindly consider the following
119. Let
So,
131. Kindly consider the following

131. Kindly go through the solution


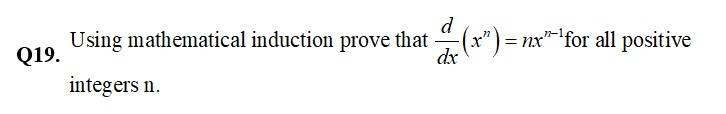
Differentiating w r t. ‘x’ we get,
50. Kindly consider the following
50. Given, sin2y + cos xy = p
Differentiating w r t ‘x’ we get,
=
{Qsin 2x = 2sin x cos x}
17. Find the relationship between a and b so that the function defined by
continuous at = 0? What about continuity at = 1?
17. Given, f (x) =
For continuity at x = 0,
f (x) = f (x) = f (0).
= 4x + 1 =
0 = 1 = 0 which is not true
Hence, f is not continuous for any value of
For x = 1,
f (x) = f (1).
4x + 1 = 4 (1) + 1
4 + 1 = 4 + 1
5 = 5.
So, f is continuous at x = 1 value of
15.
15. Given, f(x) =
For x = c < 1,
f(c) = 2
f(x) = ( 2) = 2 = f(c)
So, f is continuous at x< 1.
For x = c > 1,
f(c) = 2
f(x) = . 2 = 2 = f(c)
So, f is continuous at x 1.
For x = 1,
L.H.L. = f(x) = 2 = 2
R.H.L. = f(x) = . 2x = 2 ( 1) = 2
and f( 1) = 2
So, L.H.L. = R.H.L. = f( 1)
∴f is continuous at x = 1.
For x = 1,
L.H.L. = f(x) = . 2x = 2.1 = 2
R.H.L. = f(x) = . 2 = 2.
f(1) = 2
f(1) = L.H.L = R.H.L.
So, f is continuous at x = 1.

By repeating application of produced rule
= R×H×S×
By togarith differentiating,
Let y = u v w
Taking log, log y = log u + log v + log w
Differentiating w r t ‘x’

Differentiating w r t ‘x’ we get
Again,
Then, L.H.S =
Where c is a constant and is independent of a and b.
51. Kindly consider the following
51. Given, sin2x + cos2y = 1.
Differentiating w r t ‘x’ we get,
(sin2x + cos2y)
= 2sin x cos x + 2 cos y (- sin y)
= sin 2x- sin 2y = 0
24. Examine the continuity of , where is defined by
24. Given, f(x) =
For x = c 0,
f(c) = sin c cos c.
f (x) = (sin x cos x) = sin c cos c = f(c)
So, f is continuous at
For x = 0,
f(0) = 1
f (x) = (sin x cos x) = sin 0 cos 0 = 0 1 = 1
∴ f(x) = f (x) = f (0)
So, f is continuous at x = 0.
Find the values of so that the function is continuous at the indicated point in Exercises 26 to 29.
25.
25. Given, f(x) =
For continuity at
Take .
Putting x = such that as
So
i e,
k = 6
Similarly from
So,
k = 6
49. Kindly consider the following
49. Given, x3 + x2y + xy2 + y3 = 81.
Differentiating w r t ‘x’ we get,
=
= - (3x2 + 2xy + y2)
69. Kindly consider the following
69. Let y = cos x cos 2x cos 3x _____ (i)
Taking loge on bolk sides.
logy = log (cos x) + log (cos 2x + log (cos 3x)
= log (cos x) + log (cos 2x) + log (cos 3x)
Differentiating w r t ‘x’
= - tan x-2 tan 2x- 3 tan 3x.
= y [- tan x- 2 tan 2x- 3 tan 3x]
Putting value of y from (i) we get,
= - cos x cos 2x cos 3x [tan x + 2 tan 2x + 3 tan 3x]
70. Kindly consider the following
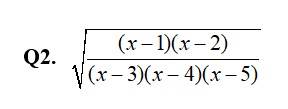
70. Kindly go through the solution

Putting value of y from the above we get,

78. Kindly consider the following
78. Let y = xx cos x
Putting 4 = xx cos x and v = we have,
y = u + v
____ (1)
As u xx cos x.
Taking log,
Log u = x cos x log x
Differentiating w r t ‘x’,
[cos x log x] + cos x log x
= x + cos x log x.
+ cos x log x.
= cos x- sin x. log x + cos x log x.
[cosx + cos x log x- sin x log x]
= xx cos x [cos x + cos x log x-x sin x log x]
And v =
So,
Hence, eqn (1) becomes,
xxcos x [cos x + cos x log x-x sin x log x]
87. Kindly consider the following
87. Given, x = 2at2 and y = at4. Differentiation w r t we get,
and
88. Kindly consider the following

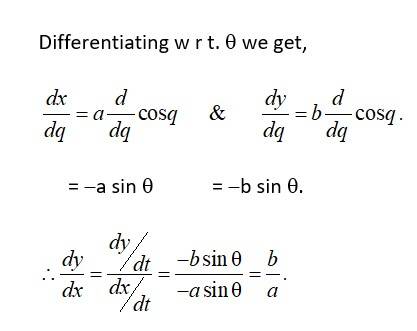
89. Kindly consider the following
89. Given, x = sin t and y = cos2t. differentiation w r t. ‘t’ we get,
= -4 sin t
90. Kindly consider the following
90. Given, x = 4t and y = Differentiating w r t. ‘t’ we get,
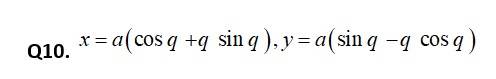

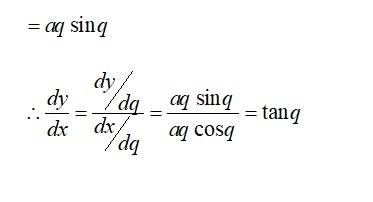
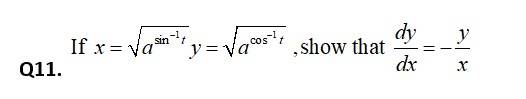
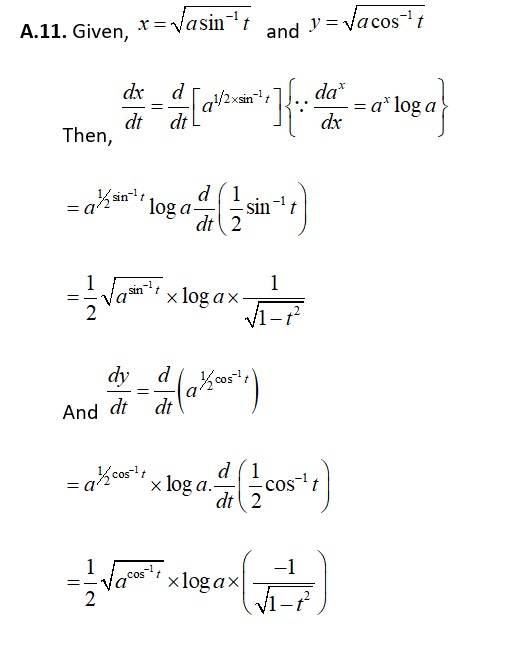
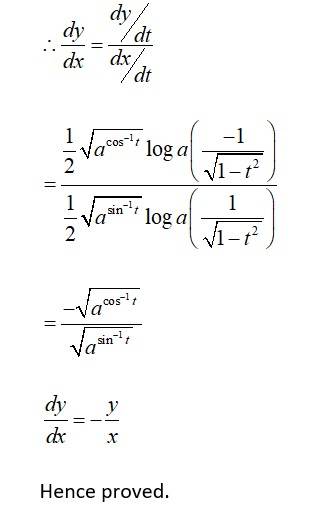
104. Kindly consider the following
104. Let
so,
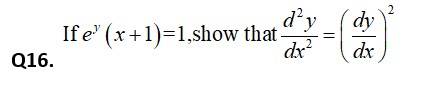

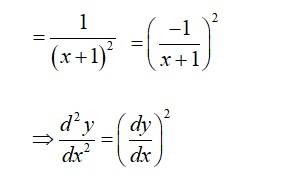
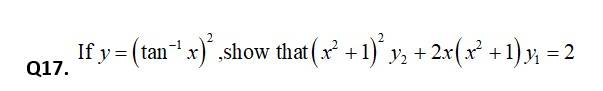
So,
Differentiating again w r t ‘x’ we get,
Hence proved.
114. If f:[-5,5] →R is a differentiable function and if f'(x) does not vanish anywhere, then prove that f(-5) ≠ f(5).
114. Solution :
It is given that f: [-5,5]? R is a differentiable function.
Since every differentiable function is a continuous function, we obtain
(a) f is continuous on [?5, 5].
(b) f is differentiable on (?5, 5).
Therefore, by the Mean Value Theorem, there exists c? (?5, 5) such that
It is also given that f' (x) does not vanish anywhere.
Hence, proved.
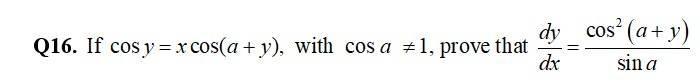
Differentiating w r t ‘y’ we get,
So,
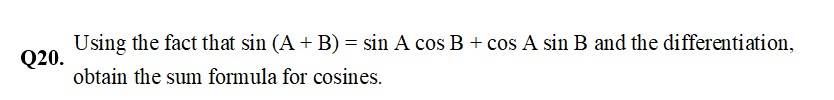
So, x = 1, x= 2 divides the real line into three disjoint intervals and
For
For
For
Hence, these polynomial fun are all continous and desirable. for all real values of x or, except x = 1 and x = 2.
ie,
For differentiavity at x = 1,
LHD =
= -2
RHD =
as L.HD ≠ R.HD
f is not differentiable at x =1.
For continuity at x = 1.
L.HL=
RHL = \ LHL = RHS
f is continuous at x = 1
For continuity & differentiability at x = 2
? LHL = RHL
f is continuous at x = 2
= 2
? LHD ≠ RHD
f is not differentiable at x = 2.
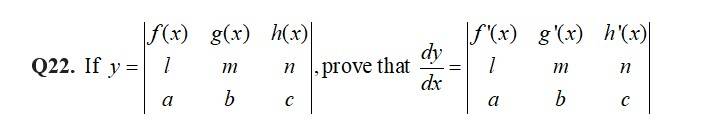
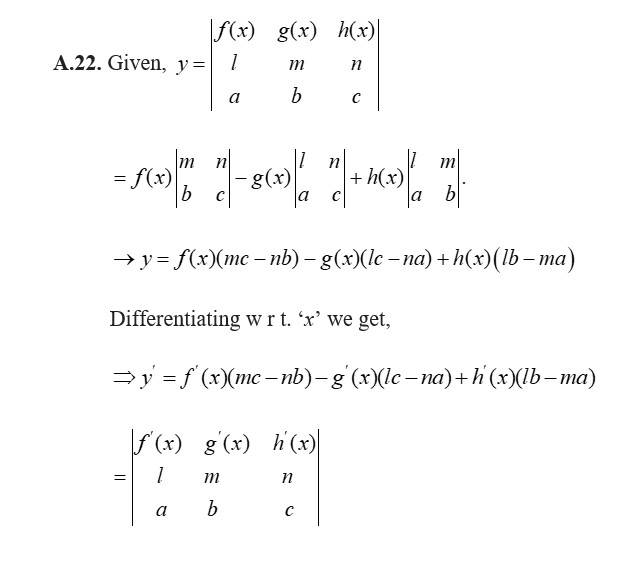
12. Is the function defined by
a continuous function?
Discuss the continuity of the function , where is defined by
12. Given, f(x) =
For x = c < 1.
F (c) = c + 5
f(x) = f x + 5 = c + 5
∴ f(x) = f(c)
So, f is continuous at x 1.
For x = c > 1
F (c) = c 5
f(x) = x 5 = c 5.
f(x) = f(c)
So, f is continuous at x 1.
For x = 1
L.H.L. = f(x) = x + 5 = 1 + 5 = 6.
R.H.L. = f(x) = x 5 = 1 5 = 4.
L.H.L. R.H.L.
f is not continuous at x = 1
So, point of discontinuity of f is at x = 1.
Discuss the continuity of the function , where is defined by
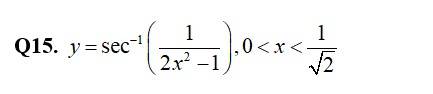

16. Find the relationship between a and b so that the function defined by
is continuous at = 3.
16. Given, f (x) = is continuous at x = 3
So, f (3) = 3a + 1
L.H.L = f (x) = ax + 1 = 3a + 1
R.H.L = f (x) = b x + 3 = 3b + 3
for continuity at x = 3,
L.H.L = R.H.L. = f (3)
3a + 1 = 3 + 3 = 3a + 1
So, 3a + 1 = 3b + 3
3a = 3b + 3 1
3a = 3b + 2.
a = b +
31. Show that the function defined by is a continuous function.
31. Given, f (x) =
Let g (x) = cos x and h (x) =
Hence, as cosine function and modulus f x are continuous h are continuous.
Then, (hog) x = h (g (x)
= h (cos x)
= f (x) is also continuous being
A composites fxn of two continuous f x
33. Find all the points of discontinuity of defined by
33. Let g (x) = is continuous being a modules f x and h (x) = is also continuous being a modules
Then, f (x) = g (x) h (x).is also continuous for all x. E. R.
Hence, there is no point of discontinuous for f (x).

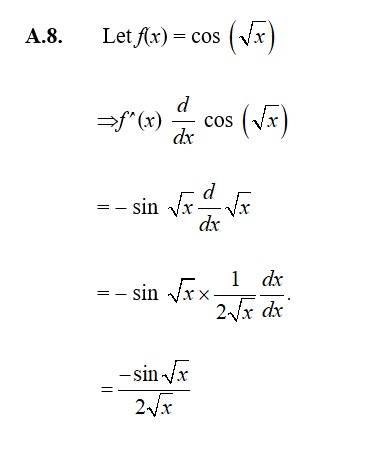
42. Prove that the function given by
is not differentiable at = 1.
42. The given f x v is
f(x) = |x- 1|, x ε R
For a differentiable f x v f at x = c,
and are finite & equal.
So, at x = 1. f(1) = |1 - 1| = 0.
Now,
L×H×L× =
=
R×H×L = = - 1.
= 1
Hence, L×H×S ¹ R×H×L×
So, f is not differentiable at x = 2.
45. Kindly consider the following
45. Given, 2x + 3y = sin y.
Differentiating w r t x. we get,
=cos y
=
72. Kindly consider the following
72. Let y = xx - 2 sin x
Putting u = xx and v = 2 sin x.
So, y = u - v
= ____ (i)
As u = xx
Log u = x log x.
So, log u = x log x.
=
x´ + log x.
= 1 + log x
= = 4 [1 + log x] = xx [1 + log x].
And v = 2sin x Log v = sin x log 2.
(sin x log 2)
sin x log 2 + log 2 = log 2. cos x.
= v log2 cos x.
= v log 2 cos x
= 2 sin x log2. cos x.
Q Eqn (i) becomes, = xx (1 + log x) - 2 sin x cos x log 2.
73. Kindly consider the following
73. Let y = (x + 3)2 (x + 4)3 (x + 5)4.
Taking loge on both sides,
log y = log (x + 3)2 + log (x + 4)3 + log (x + 5)4
= 2 log (x + 3) + 3 (log (x + 4) + 4 log (x + 5).
So,
Q log y = [2 log (x + 3) + 3 log (x + 4) + 4 log (x +5)]
= (x + 3)2 (x + 4)3 (x + 5)4
75. Kindly consider the following
75. Let y = (log x)x + x log x.
Putting u = log xx and v = x log x we get,
y = u + v
.____ (1)
As u = log xx
Taking log,
Þlog u = x [log(log x)]
Differentiating w r t x we get,
log (log x) + log (log x)
= + log (log x)
=
= (log x)x
= (log x)x- 1 [1 + log ´. log (log x)]
And v = log x
Taking log,
Log v = log x log x. = (log x)2.
Differentiating w r t ‘x’ we get,
= 2v log x
= 2. x log x.
= 2 x log x- 1 log x.
Hence eqn becomes
= (log x) x- 1[1 + log x log (log x)] + 2x log x- 1 log x
76. Kindly consider the following
76. Kindly go through the solution
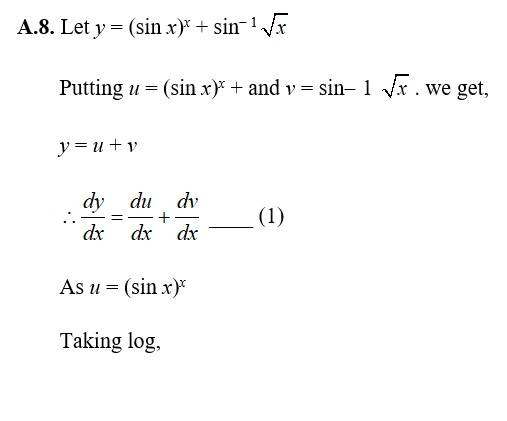
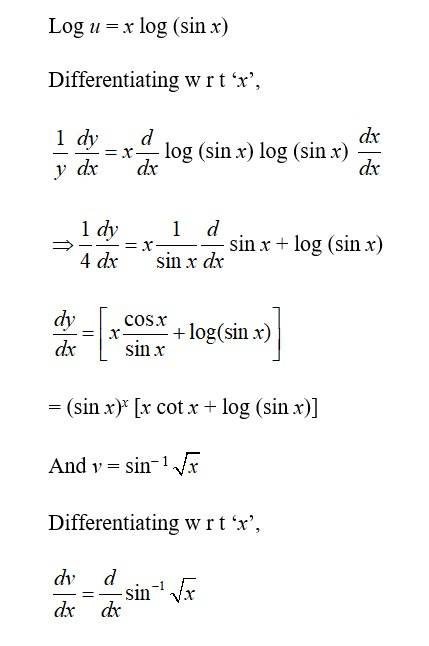
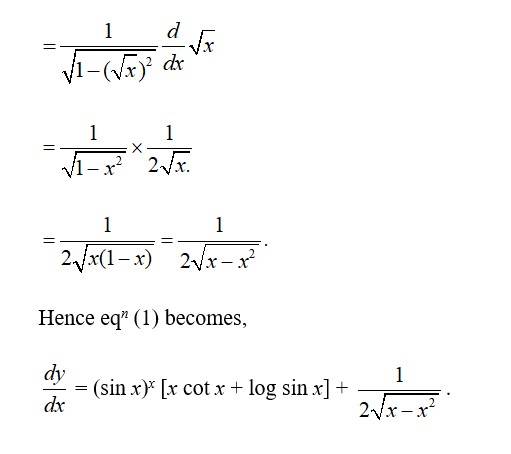
80. Kindly consider the following
80. Given, xy + yx = 1
Let 4 = xy and v =., we have,
u + v = 1.
___ (1)
So, u = xy
= log u = y log x(taking log)
Now, differentiating w r t ‘x’,
= xy- 1y + xy log x
And v = yx.
log v = x log y.
Differentiating w r t ‘x’,
= yx- 1. + yx log y.
So, eqn (1) becomes
xy- 1y + xy log x + yx - 1 + yx log y = 0
= - (xy- 1y + yx log y)
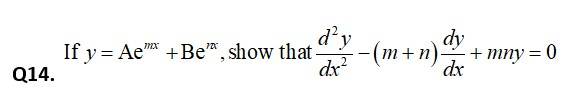
So, _______(2)
_________(3)
So, L.H.S =
= 0 = R.H.S.
1. Prove that the function f(x) = 5x 3f is continuous at x = 0, at x = – 3 and at x = 5.
1. Given, f (x) = 5x 3
At x = 0, 5x 3 = 5 0 3 = 3.
So f is continuous at x = 1.
At x = 3, 5x 3 = 5 ( 3) 3 = 15 3
= 18.
So f is continuous at x = 3.
At x = 5, .5x 3 = 5.5 3 = 25 3 = 22.
So, f is continuous at x = 5.
2. Examine the continuity of the function f(x) = 2x2 1
2. Given, f (x) = 2x2 1
At x = 3
Lim f (x) = 2 (3)2 1 = 18 1 = 17.
So, f is continuous at x = 3.
5. Prove that the function continuous at where n is a positive integer.
4. Given, f (x) = x n > n = positive.
At x = 2,
(x) = n.
f (x) = x n = n
∴ f (x) = f (x)
So f is continuous at x = n.
8.
8. Given, f(x) =
For x = c < 0,
f(c) = 1
f(x) = 1 = 1
∴f(c) = f (x)
f is continuous at x 0.
For x = c > 0,
F (c) = 1
f(x) = = 1.
∴f(c) = f(x)
f is continuous at x > 0.
For x = c 0.
L.H.L. = f(x) = ( 1) = 1
R.H.L. f(x) = 1 = 1
∴ L.H.L. R.H.L.
is now continuous at x = 0, point of discontinuity of f is at x = 0.
10.
10. Given f (x) =
For x = c < 2,
f (c) = c3 3
f (x) = x3 3 = c3 3.
So f is continuous at x 2.
For x = c > 2
f (c) = x2 + 1 = c2 + 1
f (x) = x2 + 1 = c2 + 1 = f (c)
So, f is continuous at x 2.
For x = c = 2, f (2) = 23 3 = 8 3 = 5.
L.H.L. f (x) = x3 3 = 23 3 = 5.
R.H.L. f (x) = x2 + 1 = 22 + 1 = 5
∴ R.H.L. = L.H.L. = f (2).
So, f is continuous at x = 2
Hence f has no point of discontinuity.
11.
11. Given, f (x) =
For x = c < 1.
f (c) = f (x) = c10 1.
So, f is continuous for x 1.
For x = c > 1.
f (c) = f (x) = c2
So, f is continuous for x 1.
For x = c = 1,
L.H.L = f (x) = x10 1 110 1 = 0.
R.H.L. = f (x) = x2 = 12 = 1.
∴ L.H.L R.H.L.
So, f is not continuous at x = 1.
Hence, f has point of discontinuity at x = 1.
13.
13. Given, f(x) =
For x = c such that
f(c) = 3
f(x) = 3 = 3 = f(c)
So, f is continuous in [0, 1].
For x = c = 1,
L.H.L. = f(x) = 3 = 3.
R.H.L. f(x) = 4 = 4
∴ L.H.L R.H.L.
f is discontinuity at x = 1
for x = c such that
f(c) = 4
f(x) = 4 = 4 = f(c)
So, f is continuous in
For x = c = 3
L.H.L. f(x) = 4 = 4
R.H.L. f(x) = 5 = 5.
So, f is discontinuous at x = 3.
For x = c such that
f (c) = 5.
f(x) = 5 = 5 = f(c)
So, f is continuous in
14.
14. Given f(x) =
For (c) = c < 0,
f(c) = 2c.
f(x) = 2x = 2c = f(c)
So, f is continuous at x 0
For x = c > 1,
f(c) = 4c
f(x) = 4x = 4c = f(c)
So, f is continuous at x> 1.
For x = 0
L.H.L. = f(x) = . 2x = 2 (0) = 0
R.H.L. = f(x) = . 0 = 0.
f(0) = 0.
∴ L.H.L. = R.H.L. = f(0).
So, f is continuous at x = 0.
For x = 1.
L.H.L. = f(x) = . 0 = 0
R.H.L. = f(x) = . 4x = 4 (1) = 4.
∴ L.H.L. R.H.L.
So, f is discontinuous at x = 1.
19. Is the function defined by continuous at
19. Given f (x) = x2 sin x + 5.
At x = .
f (x) = [x2 sin x + 5]
If x = then as x, h 0, so,
f (x) = [ ( + h)2 sin ( + h) + 5]
= ( + 0)2
= 2 sin cos h cos sin h + 5
= x2 0 × (1) ( 1) 0 + 5.
= 2 + 5 = f (x)
So, f is continuous at x = .
21. Discuss the continuity of the cosine, cosecant, secant and cotangent functions.
21. For two continuous fxn f(x) and g(x),
are also continuous
Let f(x) = sin x is defined x R.
Let C E R such that x = c + h. so, as x c, h 0
now, f(c) = sin c.
f(i) = sin x = sin (c + h).
= (sin c cos h + cos c sin h)
= sin c cos 0 + cos c sin 0
= sin c 1 + 0
= sin c
= f(c)
So, f is continuous.
Then, is also continuous
is also continuous
cosec x is also continuous
Let g(x) = cos x is defined x R.
Then, g(c) = cos c
g(x) = . cos x
= cos (c + h).
= (cos c cos h sin c sin h.)
= cos c cos h sin c sin h
= cos c.
= g(c)
So, g is continuous
Then, is also continuous
is also continuous
cos x is also continuous.
Hence, is also continuous
is also continuous
cot x is also continuous .
26.
26. Given f (x) =
For continuous at x = 2,
f (2) = k (2)2 = 4x.
L.H.L. =
R.H.L. =
Then, L.H.L = R.H.L. = f (2)
i e, 4x = 3
28.
28. Given, f (x)
For continuity at x = 5,
f (5) = 5k + 1
So,
i e, 5k + 1 = 10
5k = 10 1
k =
29. Find the values of a and b such that the function defined by

29. Given, f(x) =
For continuity at x = 2,
5 = 2a + b (i)
For continuous at x = 10,
10a + b = 21 (2).
So, e q (2) 5 e q (1) we get,
10a + b 5 (2a + b) = 21 5 5.
10a + b 10a 5b = 21 25.
4b = 4
b = 1.
And putting b = 1 in e q (1),
2a = 5 b = 5 1 = 4
Hence, a = 2 and b = 1.
30. Show that the function defined by is a continuous function
30. Given f (x) = cos (x2)
Let g (x) = cos x is a lregononuie fa (cosine) which is continuous function
and let h (x) = x2 is a polynomial f xn which is also continuous
Hence (goh) x = g (h (x)
= g (x)2
= cos (x2)
= f (x)
is also a continuous f x being a composite fxn of how continuous f x
32. Examine that sin is a continuous function.
32. Given, f (x) = sin
Let g (x) = sin x and h (x) = then as sine f x and modulus f x are continuous in x e R
g and h are continuous.
So, (goh) (x) = g (h (x) = g (|x|) = sin |x| = f (x)
Is a continuous f x being a competitive f x of two continuous f x.
34. Kindly Consider the following
34. Let f (x) = sin (x2 + 5)
Differentiating w. r t. x we get,
f'¢ (x) = sin (x2 + 5)
= cos (x2 + 5) = cos (x2 + 5)
= cos (x2 + 5) [2x].
= 2x cos (x2 + 5).
35. Kindly consider the following
35. Let f (x) = cos (sin x).
f' (x) cos (sin x)
= - sin (sin x) sin x
= - sin (sin x) cos x.
36. Kindly consider the following
36. Let f (x) = sin (ax + b)
f' (x) = sin (ax + b)
= cos (ax + b) (ax + b)
= a cos (ax + b).
37. Kindly consider the following

37. Kindly go through the solution
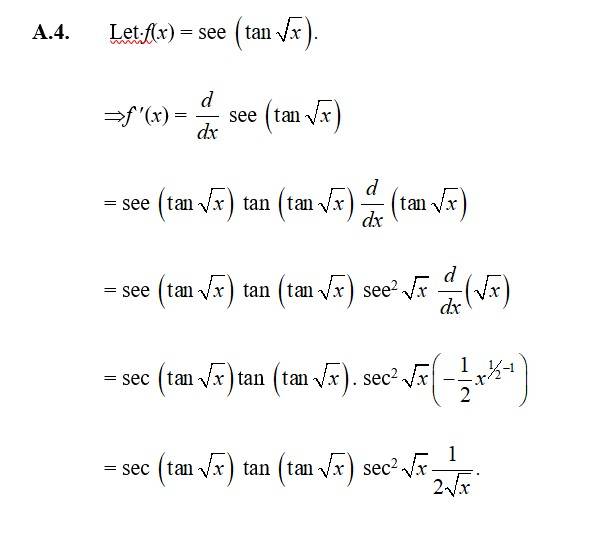
38. Kindly consider the following
38. Let f(x) =
f'(x) =
=
=
39. Kindly consider the following
39. Let f (x) = cos (x3) sin2 (x5).
f' (x) = cos (x3) sin2 (x5) + sin2 (x5) cos (x3)
= cos (x3) 2sin (x5) sin (x5) + sin2 (x5) [sin (x3)] x3.
= 2 cos (x3) sin (x5). cos (x5) (x5) - sin2 (x5) sin (x3). 3x2
= 2. cos (x3) sin (x5) cos (x5). 5 - 3x2sin2 (x5) sin (x3)
= x2 sin (x5). [2x2 cos (x3) cos (x5) - 3 sin (x5) sin x3].
44. Find in the following:
44. Kindly go through the solution
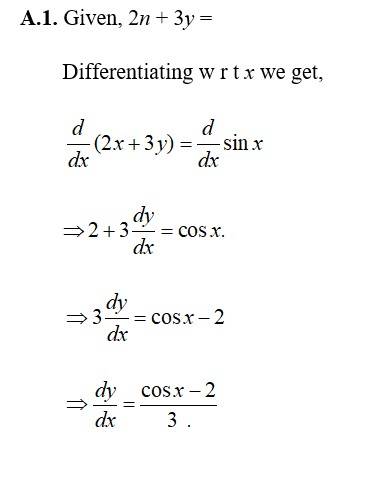
46. Kindly consider the following
46. Given, ax + by2 = cos y.
Differentiating w r t ‘x’ we get,
= a + b 2y = - sin y + sin y = -a
=
= 2by

54. Kindly consider the following
54. Kindly go through the solution
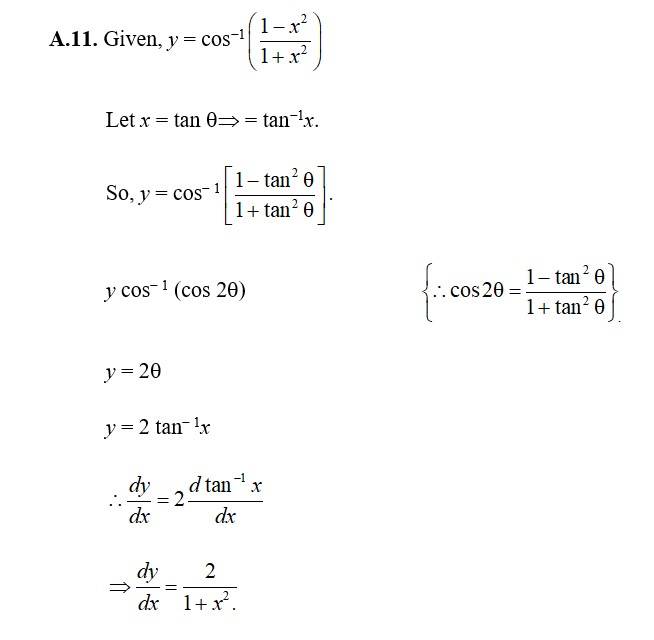
55. Kindly consider the following
55. Kindly go through the solution
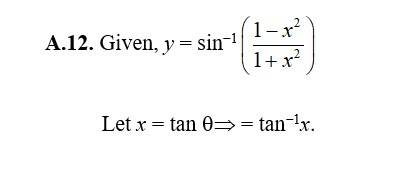
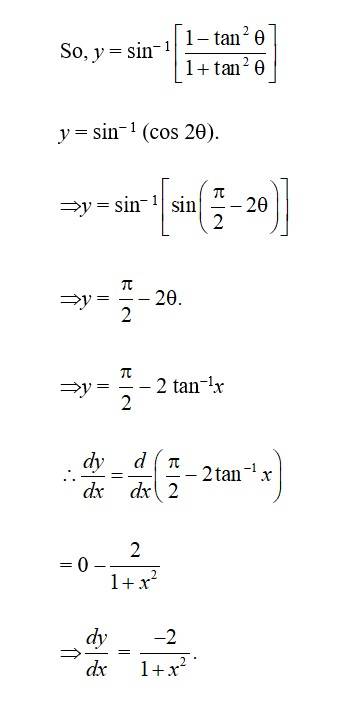
56. Kindly consider the following
56. Kindly go through the solution
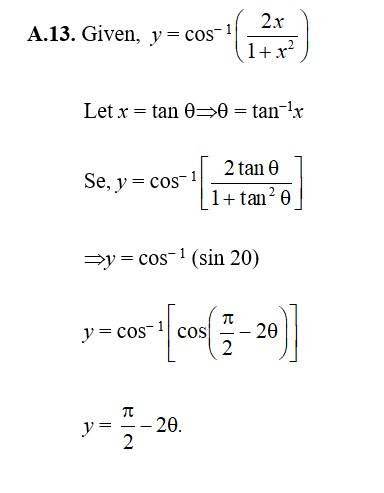
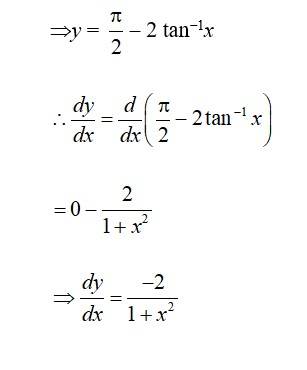
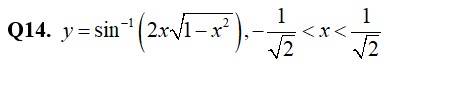

60. Kindly consider the following
60. Kindly go through the solution
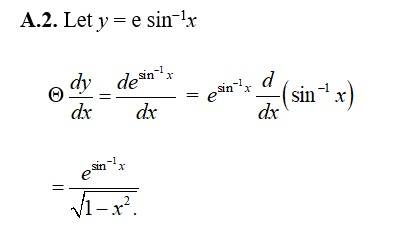
61. Kindly consider the following
ex3
61. Kindly go through the solution
Let y = ex3

62. Kindly consider the following
62. Kindly go through the solution


63. Kindly consider the following
63. Let y = log (cos ex).
log (cos ex)
(cos ex)
= -
= -ex [tan ex]
65. Kindly consider the following

65. Kindly go through the solution
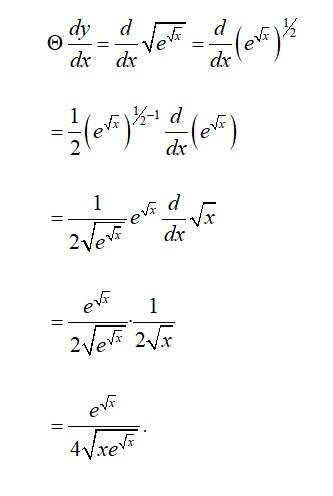
66. Kindly consider the following
66. Let y = log (log x)
67. Kindly consider the following
67.
68. Kindly consider the following
68. Let y = cos (log x + ex)
cos (log x + ex)
= - sin (log x + ex) (log x + ex)
= - sin (log x + ex)
sin (log x + ex).
71. Kindly consider the following
71. Let y = (log x) cos x
Taking loge on both sides,
Log y = cos x [log (log x)]
Differentiating w r t ‘x’ we get,
log (log x) +log (log x)
+ log (log x) (- sin x)
- sin x log (log x)
=
74. Kindly consider the following
74 . Let y = +
Putting u = and v = we get,
y = u + v
_____ (1)
As u =
Taking log,
= log u = x log
Differentiating w r t ‘x’ we get,
+ log 1.
And v = x
Taking log, log v = log x
Differentiating W r t ‘x’,
log x + log x
+ log x
= v =
Hence, eqn (1) becomes,
79. Kindly consider the following
Find of the functions given in Exercises 12 to 15.
79. Let y = (x cos x) x + (x sin)
Putting u = (x cos x)x and v = (x sin x) we, have,
y = u + v
____ (1)
As u = (x cos x)x :
Taking log,
Log u = x log (x cos x)
= x [log x + log (cos x)]
Differentiating w r t ‘x’ we get,
[log x + log (cos x)] + [log x + dog (cos x)]
+ [log x +log (cos x)]
+ log x + log (cos x)
= 1 -x tan x + log (x cos x)
= 4 [1 -x tan x + log (x cose)]
=(x cos x)x (x cos x)x [1 -x tan + log + log (x cos x)]
And v = (x sin x)
Taking log, log v = log (x sin x)
(log x + log sin x)
Differentiating w r t ‘x’
(log x + log sin x) + (log x + log sin x)
+ log x + log sin x)
=
= (x sin x)
Q Eqn (1) becomes,
= (x cos x)x [1 -x tan + log (x cos x)] + (x sin x)
= (x cos x)x [1 -x tan x + log (x cos x)] + (x sin x)
Find of the functions given in Exercises 12 to 15.
82. Kindly consider the following
82. Given, (cos x)y = (cos y)x
Taking log, y log (cos x) = x log (cos y)
Differentiating w r t ‘x’ we get,
= log (cos x) + log (cos x) log (cos y) + dog (cos y)
= y´ cos x + log (cos x) = x´
= log (cos x) + x tan
= y tan x + log (cos y )
83. Kindly consider the following
83. Given, xy = ex-y.
Taking log,
log (x + y) = log (ex-y).
=logx + log y = (x-y) log e.
= logx +log y = x -y {Q log e = 1}
Differentiating w r t ‘x’ we get,
91. Kindly consider the following
91. Given,
Differentiating w r t we get,
Find the second order derivatives of the functions given in Exercise 1 to 10
95.
95. Let y = x2 + 3x + 2
So, (differentiation w r t 'x')
(Again “ “ ) = 2
96. Kindly consider the following
96. Let
So,
97. Kindly consider the following
97. Let
So,
98. Kindly consider the following
98. Let
So,
99. Kindly consider the following
99. Let
So,
100. Kindly consider the following
100. Let
so,
101. Kindly consider the following
101. Let
So,
102. Kindly consider the following
102. Let
So,
103 Kindly consider the following
103. Let
So,
105. Kindly consider the following
105. Given,
Differentiating w r t x we get,
Differentiating again w r t. ‘x’ we get,
. Hence proved.
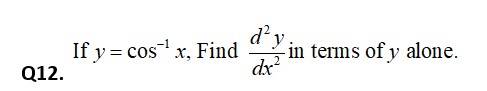
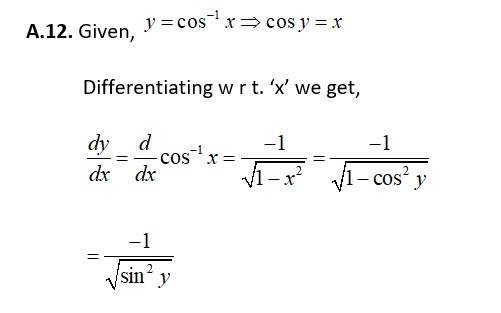
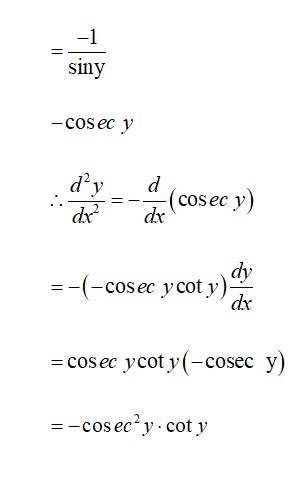
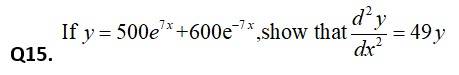
So,
112. Verify Rolle’s Theorem for the function
112. Given, , being polynomial function is continuous in and also differentiable in .
Therefore,
The value of at -4 and 2 coincides.
Rolle’s Theorem states that there is a point such that
Therefore,
Hence,
Thus,
Hence, Rolle’s Theorem is verified.
113. Examine if Rolle’s Theorem is applicable to any of the following functions. Can you say something about the converse of Rolle’s Theorem from these examples?
for
for
for
113. Solution:
By Rolle’s Theorem, for a function if
f is continuous on
f is differentiable on
f(a)= f(b)
then, there exists some such that
therefore, Rolle’s Theorem is not applicable to those functions that do not satisfy any of the three conditions of the hypothesis.
for
It is evident that the given function f(x) is not continuous at every integral point.
In particular, f(x) is not continuous at x=5 and x=9
f(x) is not continuous in
Also,
The differentiability of f in is checked as follows.
Let n be an integer such that .
The left hand limit of f at x=n is,
The right hand limit of f at x=n is,
Since the left and right hand limits of f at x=n are not equal, f is not differentiable at x=n
f is not differentiable in (5,9).
It is observed that f does not satisfy all the conditions of the hypothesis of Rolle’s Theorem.
Hence, Rolle’s Theorem is not applicable for for
for
It is evident that the given function f(x) is not continuous at every integral point.
In particular, f(x) is not continuous at x=-2 and x=2
f(x) is not continuous in .
Also,
The differentiability of f in is checked as follows.
Let n be an integer such that .
The left hand limit of f at x=n is,
The right hand limit of f at x=n is,
Since the left- and right-hand limits of f at x=n are not equal, f is not differentiable at x=n
f is not differentiable in (-2,2).
It is observed that f does not satisfy all the conditions of the hypothesis of Rolle’s Theorem.
Hence, Rolle’s Theorem is not applicable for for
for
It is evident that f, being a polynomial function, is continuous in and is differentiable on (1,2).
It is observed that f does not satisfy a condition of the hypothesis of Rolle’s Theorem.
Hence, Rolle’s Theorem is not applicable for for .
115. Verify Mean Value Theorem, if in the interval [a,b], where a = 1 and b = 4.
115.
Solution :
The given function is f, being a polynomial function, is continuous in [1, 4] and is differentiable in (1, 4) whose derivative is 2x − 4.
Mean Value Theorem states that there is a point c ∈ (1, 4) such that f' (c) = 1
Hence, Mean Value Theorem is verified for the given function.
116. Verify Mean Value Theorem, if in the interval [a, b], where a = 1 and b = 3. Find all c ∈ (1, 3) for which f'(c) = 0
116. Solution:
The given function f is f, being a polynomial function, is continuous in [1, 3] and is differentiable in (1, 3) whose derivative is 3x2 − 10x − 3.
Mean Value Theorem states that there exists a point c ∈ (1, 3) such that f'(c) = - 10
Hence, Mean Value Theorem is verified for the given function and c = 7/3 ∈ (1,3) is the only point for which f'(c) = 0
117. Examine the applicability of Mean Value Theorem for all three functions given in the above exercise 2.
117. Solution :
Mean Value Theorem states that for a function f[a,b] →R, if
(a) f is continuous on [a, b]
(b) f is differentiable on (a, b)
then, there exists some c ∈ (a, b) such that
Therefore, Mean Value Theorem is not applicable to those functions that do not satisfy any of the two conditions of the hypothesis.
for
It is evident that the given function f (x) is not continuous at every integral point.
In particular, f(x) is not continuous at x = 5 and x = 9
⇒ f (x) is not continuous in [5, 9].
The differentiability of f in (5, 9) is checked as follows.
Let n be an integer such that n ∈ (5, 9).
The right hand limit of f at x=n is,
Since the left and right hand limits of f at x = n are not equal, f is not differentiable at x = n
∴f is not differentiable in (5, 9).
It is observed that f does not satisfy all the conditions of the hypothesis of Mean Value Theorem.
Hence, Mean Value Theorem is not applicable for for .
(ii)
It is evident that the given function f (x) is not continuous at every integral point.
In particular, f(x) is not continuous at x = −2 and x = 2
⇒ f (x) is not continuous in [−2, 2].
The differentiability of f in (−2, 2) is checked as follows.
Let n be an integer such that n ∈ (−2, 2).
The right hand limit of f at x=n is,
Since the left and right hand limits of f at x = n are not equal, f is not differentiable at x = n
∴f is not differentiable in (−2, 2).
It is observed that f does not satisfy all the conditions of the hypothesis of Mean Value Theorem.
Hence, Mean Value Theorem is not applicable for for
(iii) for
It is evident that f, being a polynomial function, is continuous in [1, 2] and is differentiable in (1, 2).
It is observed that f satisfies all the conditions of the hypothesis of Mean Value Theorem.
Hence, Mean Value Theorem is applicable for for
It can be proved as follows.
118. Kindly consider the following
118. Let
So,
120. Kindly consider the following
120. Let
Taking log,
Differentiating w r t. x,
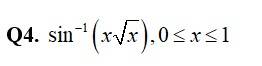
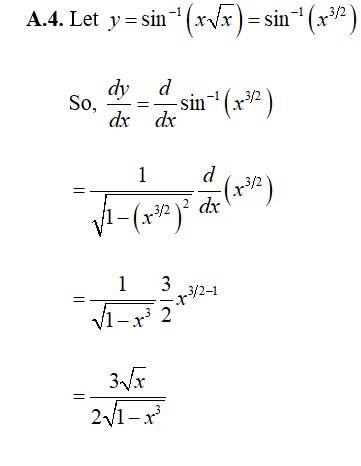
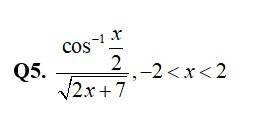
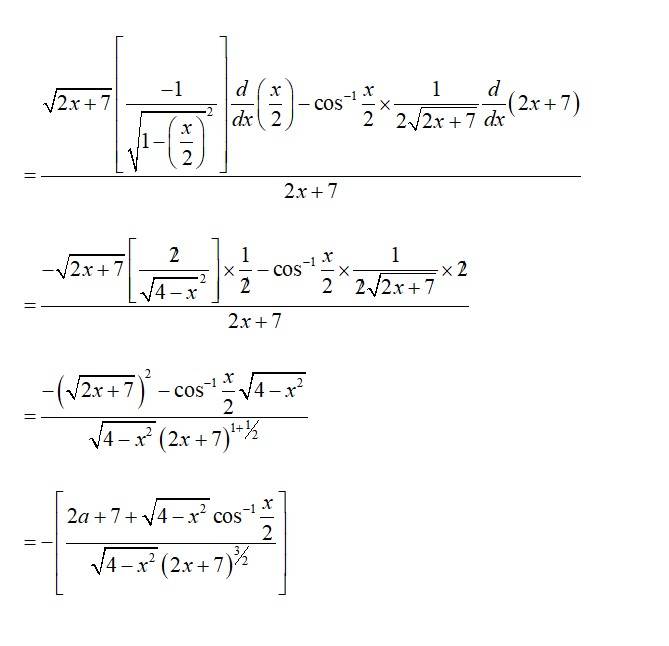
124. Kindly consider the following
124. Let
Taking log,
Differentiating w r t. x, we get,
So,
126. Kindly consider the following
126. Let
Taking log,
Differentiating w r t ‘x’ we get,

So,
_________(1)
Where
(Taking log)
(Differentiation w r t ‘x’)
Hence eqn (1) becomes,
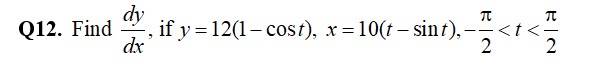
Differentiating w r t ‘t’ we get,
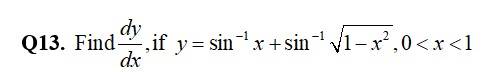
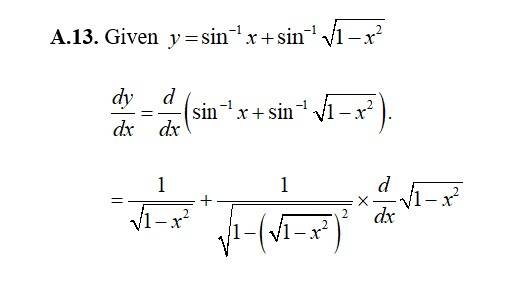
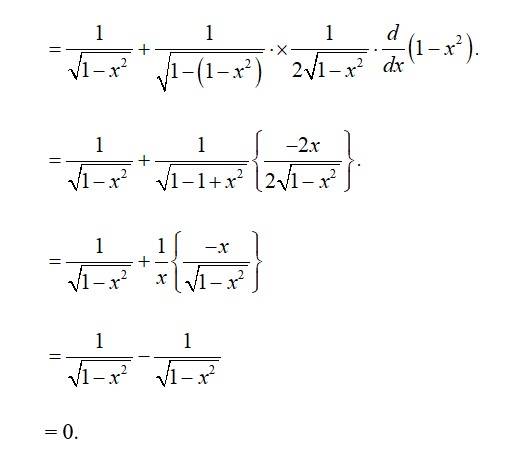
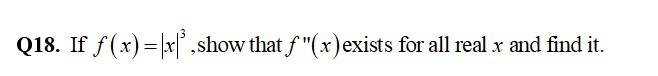
For
and
For
so,
Hence,
Maths Ncert Solutions class 12th Exam
