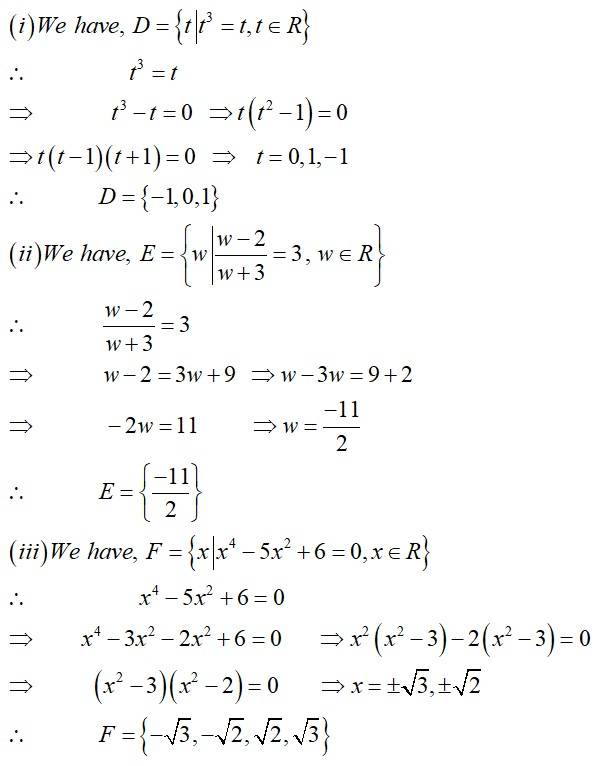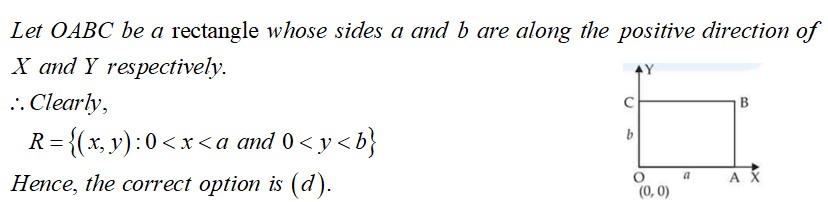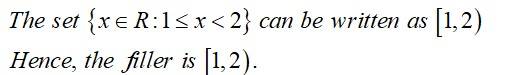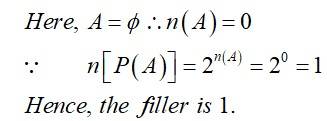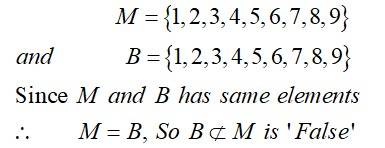If A is any set, then A ⊂ A

Since every set is a subset of itself. So, it is 'True'.

Given that M = {1, 2, 3, 4, 5, 6, 7, 8, 9} and if B = {1, 2, 3, 4, 5, 6, 7, 8, 9}, then B ⊄ M

M = { 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 } a n d B = { 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 } Since M and B has same elements ∴ M = B , S o B ⊄ M ? ? i s ' F a l s e '

The sets {1, 2, 3, 4} and {3, 4, 5, 6} are equal.

False, Since the two sets do not contain the same elements.

Q ∪ Z = Q, where Q is the set of rational numbers and Z is the set of integers.

True, Since every integer is a rational number ∴ Z ⊂ Q , S o Q ∪ Z = Q .

Let sets R and T be defined as R = {x ∈ Z | x is divisible by 2} T = {x ∈ Z | x is divisible by 6}. Then T ⊂ R

W e c a n w r i t t e n t h e g i v e n s e t s i s R o a s t e r f o r m R = { … , − 8 , − 6 , − 4 , − 2 , 0 , 2 , 4 , 6 , 8 , … } a n d T = { … , − 1 8 , − 1 2 , − 6 , 0 , 6 , 1 2 , 1 8 … } Since every element of T is present in R. So, T⊂R. H e n c e , t h e s t a t e m e n t i s ' T r u e ' .

The function, f(x) = (3x – 7)x²/³, x ∈ R, is increasing for all x lying in:

(-∞, 0) U (14/15, ∞)

(-∞, 14/15)

(-∞, 0) U (14/3, ∞)

The foot of the perpendicular drawn from the point (4,2,3) to the line joining the points (1, −2,3) and (1,1,0) lies on the plane:

2x + y − z = 1

x - y - 2z = 1

x - 2y + z = 1

x + 2y - z = 1

If α and β are the roots of the equation x² + px + 2 = 0 and 1/α and 1/β are the roots of the equation 2x² + 2qx + 1 = 0, then (α - 1/β)(β - 1/α)(α + 1/β)(β + 1/α) is equal to:

9/4(9 + p²)

9/4(9 + q²)

9/4(9 - q²)

A hyperbola having the transverse axis of length √2 has the same foci as that of the ellipse 3x² + 4y² = 12, then this hyperbola does not pass through which of the following points?

(√3/2, 1/√2)

(1, -1/√2)

(-√3/2, 1)

(√5/2, 0)

Let P be a point on the parabola, y² = 12x and N be the foot of the perpendicular drawn from P on the axis of the parabola. A line is now drawn through the mid-point M of PN, parallel to its axis which meets the parabola at Q. If the y-intercept of the line NQ is 4/3, then:

PN = 3

The proposition p →~ (p ∧~ q) is equivalent to:

(~ p) v q

(~ p) ∧ q

(~ p) v (~ q)

The area (in sq. units) of the region {(x, y): 0 ≤ y ≤ x² + 1, 0 ≤ y ≤ x + 1, 1/2 ≤ x ≤ 2} is:

24/43

16/79

The solution curve of the differential equation, (1 + e⁻ˣ)(1 + y²)dy/dx = y², which passes through the point (0,1), is

y² = 1 + ylogₑ((1+e⁻ˣ)/2)

y² + 1 = y(logₑ((1+eˣ)/2) + 2)

y² + 1 = ylogₑ((1+e⁻ˣ)/2)

y² + 1 = y(logₑ((1+e⁻ˣ)/2) + 2)

If Δ = |x-2 2x-3 3x-4| |2x-3 3x-4 4x-5| |3x-5 5x-8 10x-17| = Ax³ + Bx² + Cx + D, then B + C is equal to:

-3

Consider the two sets: A = {m ∈ R : both the roots of x² – (m + 1)x + m + 4 = 0 are real } and B = [−3,5). Which of the following is not true?

A − B = (-∞, −3) U (5, ∞)

A ∩ B = {−3}

B − A = (-3,5)

A U B = R

The lines r = (î − ĵ) + l(2î + k) and r = (2î – ĵ) + m(î + ĵ – k)

Do not intersect for any values of l and m

Intersect when l = 2 and m = 1/2

Intersect for all values of l and m

Maths NCERT Exemplar Solutions Class 11th Chapter One: Overview, Questions, Preparation

Q: Write the following sets in the roaster form (i) A = {x: x ∈ R, 2x + 11 = 15} (ii) B = {x | x2 = x, x ∈ R} (iii) C = {x | x is a positive factor of a prime number p}

( i ) W e h a v e , A = { x : x ∈ R , 2 x + 1 1 = 1 5 } ∴ 2 x + 1 1 = 1 5 ⇒ 2 x = 1 5 − 1 1 ⇒ 2 x = 4 ⇒ x = 2 ∴ A = { 2 } ( i i ) W e h a v e , B = { x | x 2 = x , x ∈ R } ∴ x 2 = x ⇒ x 2 − x = 0 ⇒ x ( x − 1 ) = 0 ⇒ x = 0 , 1 ∴ B = { 0 , 1 } ( i i i ) W e h a v e , C = { x | x i s a p o s i t i v e f a c t o r o f p r i m e n u m b e r p . } Since, positive factors of a prime number are 1 and the number itself. ∴ C = { 1 , p }

Q: Write the following sets in the roaster form (i) D = {t | t3 = t, t ∈ R} (ii) E = {w | =3, w ∈ R} (iii) F = {x | x4 – 5x2 + 6 = 0, x ∈ R}

(i)We have, D={t|t3=t,t∈R}∴ t3=t⇒ t3−t=0 ⇒t(t2−1)=0⇒t(t−1)(t+1)=0 ⇒ t=0,1,−1∴ D={−1,0,1}(ii)We have, E={w|w−2w+3=3, w∈R}∴ w−2w+3=3⇒ w−2=3w+9 ⇒w−3w=9+2⇒ −2w=11 ⇒w=−112∴ E={−112}(iii)We have, F={x|x4−5x2+6=0,x∈R}∴ x4−5x2+6=0⇒ x4−3x2−2x2+6=0 ⇒x2(x2−3)−2(x2−3)=0⇒ (x2−3)(x2−2)=0 ⇒x=±3,±2∴ F={−3,−2,2,3}

Q: If Y = {x | x is a positive factor of the number 2p – 1 (2p – 1), where 2p – 1 is a prime number}. Write Y in the roaster form.

G i v e n , Y = { x | x i s a p o s i t i v e f a c t o r o f t h e n u m b e r 2 p − 1 ( 2 p − 1 ) , w h e r e 2 p − 1 i s a p r i m e n u m b e r } . Since, the factors of 2p−1 are 1,2,22,23,…,2p−1 and factors of 2p−1 are 1 and 2p−1 ∴ Y = { 1 , 2 , 2 2 , 2 3 , … , 2 p − 1 , 2 p − 1 } = 2 ( 2 p − 1 ) , 2 2 ( 2 p − 1 ) , … , 2 p − 1 ( 2 p − 1 )

Q: Given L = {1, 2, 3, 4}, M = {3, 4, 5, 6} and N = {1, 3, 5} Verify that L – (M ∪ N) = (L – M) ∩ (L – N)

G i v e n , L = { 1 , 2 , 3 , 4 } , M = { 3 , 4 , 5 , 6 } a n d N = { 1 , 3 , 5 } ∴ M ∪ N = { 1 , 3 , 4 , 5 , 6 } L − M ∪ N = { 2 } N o w , L − M = { 1 , 2 } , L − N = { 2 , 4 } ∴ ( L − M ) ∩ ( L − N ) = { 2 } H e n c e , L − M ∪ N = ( L − M ) ∩ ( L − N ) .

Q: The set {x ∈ R: 1 ≤ x < 2} can be written as ______________.

T h e s e t { x ∈ R : 1 ≤ x < 2 } c a n b e w r i t t e n a s [ 1 , 2 ) H e n c e , t h e f i l l e r i s [ 1 , 2 ) .

Updated on Sep 12, 2025 14:34 IST

By Vishal Baghel, Executive Content Operations

Table of content

Sets Short Answer Type Questions
Sets Objective Type Questions
Sets Fill in the blanks
Sets True and False Type Questions

Sets Short Answer Type Questions

Write the following sets in the roaster form

(i) A = {x: x ∈ R, 2x + 11 = 15}

(ii) B = {x | x² = x, x ∈ R}

(iii) C = {x | x is a positive factor of a prime number p}

Write the following sets in the roaster form

(i) D = {t | t³= t, t ∈ R}

(ii) E = {w | =3, w ∈ R}

(iii) F = {x | x⁴ – 5x² + 6 = 0, x ∈ R}

Commonly asked questions

State which of the following statements a true and which are false. Justify your answer.

(i) 35 ∈ {x | x has exactly four positive factors}.

(ii) 128 ∈ {y | the sum of all the positive factors of y is 2y}

(iii) 3 ∉ {x | x4 – 5x3 + 2x2 – 112x + 6 = 0}

(iv) 496 ∉ {y | the sum of all the positive factors of y is 2y}.

$\begin{array}{l} (i) G i v e n t h a t : 35 \in {x | x h a s e x a c t l y f o u r p o s i t i v e f a c t o r} \\ ∴ F a c t o r s o f 35 a r e 1, 5, 7, 35 \\ H e n c e, t h e s t a t e m e n t (i) i s' T r u e' . \\ (i i) G i v e n t h a t : 128 \in {y | t h e s u m o f a l l p o s i t i v e f a c t o r s o f y i s 2 y} \\ ∴ F a c t o r s o f 128 a r e 1, 2, 4, 8, 16, 32, 64 a n d 128 . \\ S u m o f a l l f a c t o r s = 1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 \\ = 255 \neq 2 \times 128 \\ H e n c e, t h e s t a t e m e n t (i i) i s' F a l s e' . \\ (i i i) G i v e n t h a t : 3 \in {x | x^{4} - 5 x^{3} + 2 x^{2} - 112 x + 6 = 0} \\ ∴ x^{4} - 5 x^{3} + 2 x^{2} - 112 x + 6 = 0 \\ N o w f o r x = 3, w e h a v e \\ {(3)}^{4} - 5 {(3)}^{3} + 2 {(3)}^{2} - 112 (3) + 6 \\ \Rightarrow 81 - 135 + 18 - 336 + 6 \Rightarrow - 366 \neq 0 \\ H e n c e, t h e s t a t e m e n t (i i i) i s' T r u e' . \\ (i v) G i v e n t h a t : 496 \notin {y | t h e s u m o f a l l p o s i t i v e f a c t o r s o f y i s 2 y} \\ ∴ T h e p o s i t i v e f a c t o r s o f 496 a r e 1, 2, 4, 8, 16, 31, 62, 124, 248 a n d 496 . \\ ∴ T h e s u m o f a l l p o s i t i v e f a c t o r s = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 + 496 \\ = 992 = 2 \times 496 \\ H e n c e, t h e s t a t e m e n t (i v) i s' F a l s e' . \end{array}$

Write the following sets in the roaster form

(i) A = {x: x ∈ R, 2x + 11 = 15}

(ii) B = {x | x2 = x, x ∈ R}

(iii) C = {x | x is a positive factor of a prime number p}

$\begin{array}{l} (i) W e h a v e, A = {x : x \in R, 2 x + 11 = 15} \\ ∴ 2 x + 11 = 15 \\ \Rightarrow 2 x = 15 - 11 \\ \Rightarrow 2 x = 4 \Rightarrow x = 2 \\ ∴ A = {2} \\ (i i) W e h a v e, B = {x | x^{2} = x, x \in R} \\ ∴ x^{2} = x \\ \Rightarrow x^{2} - x = 0 \\ \Rightarrow x (x - 1) = 0 \\ \Rightarrow x = 0, 1 \\ ∴ B = {0, 1} \\ (i i i) W e h a v e, C = {x | x i s a p o s i t i v e f a c t o r o f p r i m e n u m b e r p .} \\ Since, p o s i t i v e f a c t o r s o f a p r i m e n u m b e r a r e 1 a n d t h e n u m b e r i t s e l f . \\ ∴ C = {1, p} \end{array}$

Write the following sets in the roaster form

(i) D = {t | t3 = t, t ∈ R}

(ii) E = {w | =3, w ∈ R}

(iii) F = {x | x4 – 5x2 + 6 = 0, x ∈ R}

$\begin{array}{l} (i) W e h a v e, D = {t | t^{3} = t, t \in R} \\ ∴ t^{3} = t \\ \Rightarrow t^{3} - t = 0 \Rightarrow t (t^{2} - 1) = 0 \\ \Rightarrow t (t - 1) (t + 1) = 0 \Rightarrow t = 0, 1, - 1 \\ ∴ D = {- 1, 0, 1} \\ (i i) W e h a v e, E = {w | \frac{w - 2}{w + 3} = 3, w \in R} \\ ∴ \frac{w - 2}{w + 3} = 3 \\ \Rightarrow w - 2 = 3 w + 9 \Rightarrow w - 3 w = 9 + 2 \\ \Rightarrow - 2 w = 11 \Rightarrow w = \frac{- 11}{2} \\ ∴ E = {\frac{- 11}{2}} \\ (i i i) W e h a v e, F = {x | x^{4} - 5 x^{2} + 6 = 0, x \in R} \\ ∴ x^{4} - 5 x^{2} + 6 = 0 \\ \Rightarrow x^{4} - 3 x^{2} - 2 x^{2} + 6 = 0 \Rightarrow x^{2} (x^{2} - 3) - 2 (x^{2} - 3) = 0 \\ \Rightarrow (x^{2} - 3) (x^{2} - 2) = 0 \Rightarrow x = \pm \sqrt[]{3}, \pm \sqrt[]{2} \\ ∴ F = {- \sqrt[]{3}, - \sqrt[]{2}, \sqrt[]{2}, \sqrt[]{3}} \end{array}$

If Y = {x | x is a positive factor of the number

2p – 1 (2p – 1), where 2p – 1 is a prime number}. Write Y in the roaster form.

$\begin{array}{l} G i v e n, Y = {x | x i s a p o s i t i v e f a c t o r o f t h e n u m b e r 2^{p - 1} (2^{p} - 1), w h e r e 2^{p - 1} i s a p r i m e n u m b e r} . \\ Since, t h e f a c t o r s o f 2^{p - 1} a r e 1, 2, 2^{2}, 2^{3}, \dots, 2^{p - 1} a n d f a c t o r s o f 2^{p} - 1 a r e 1 a n d 2^{p - 1} \\ ∴ Y = {1, 2, 2^{2}, 2^{3}, \dots, 2^{p - 1}, 2^{p} - 1} \\ = 2 (2^{p} - 1), 2^{2} (2^{p} - 1), \dots, 2^{p - 1} (2^{p} - 1) \end{array}$

Given L = {1, 2, 3, 4}, M = {3, 4, 5, 6} and N = {1, 3, 5}

Verify that L – (M ∪ N) = (L – M) ∩ (L – N)

$\begin{array}{l} G i v e n, L = {1, 2, 3, 4}, M = {3, 4, 5, 6} a n d N = {1, 3, 5} \\ ∴ M \cup N = {1, 3, 4, 5, 6} \\ L - M \cup N = {2} \\ N o w, L - M = {1, 2}, L - N = {2, 4} \\ ∴ (L - M) \cap (L - N) = {2} \\ H e n c e, L - M \cup N = (L - M) \cap (L - N) . \end{array}$

If A and B are subsets of the universal set U, then show that

(i) A ⊂ A ∪ B

(ii) A ⊂ B ⇔ A ∪ B = B

(iii) (A ∩ B) ⊂ A

$\begin{array}{l} (i) G i v e n t h a t : A \subset U a n d B \subset U \\ L e t x \in A o r x \in B \\ \Rightarrow x \in A \cup B \\ H e n c e, A \subset (A \cup B) \\ (i i) I f A \subset B \\ T h e n l e t x \in A \cup B \\ \Rightarrow x \in A o r x \in B \\ \Rightarrow A \cup B \subset B \dots (i) \\ B u t B \subset A \cup B \dots (i i) \\ F r o m e q . (i) a n d (i i), w e g e t \\ A \cup B = B \\ L e t y \in A \Rightarrow y \in (A \cup B) \Rightarrow y \in B \\ \Rightarrow y \in B \Leftrightarrow A \cup B = B \\ (i i i) L e t x \in A \cap B \\ \Rightarrow x \in A a n d x \in B \Rightarrow x \in A \\ S o, A \cap B \subset A \end{array}$

Given that N = {1, 2, 3, ..., 100}. Then write

(i) The subset of N whose elements are even numbers.

(ii) The subset of N whose element are perfect square numbers.

^{$\begin{array}{l} W e a r e g i v e n t h a t : N = {1, 2, 3, 4, 5, \dots, 100} \\ (i) Required s u b s e t w h o s e e l e m e n t s a r e e v e n \\ = {2, 4, 6, 8, \dots, 100} \\ (i i) Required s u b s e t w h o s e e l e m e n t s a r e p e r f e c t s q u a r e s \\ = {1, 4, 9, 16, 25, 36, \dots, 100} \end{array}$}

If X = {1, 2, 3}, if n represents any member of X, write the following sets containing all numbers represented by

(i) 4n

(ii) n + 6

(iii) $\frac{n}{2}$

(iv) n – 1

$\begin{array}{l} W e a r e g i v e n t h a t : X = {1, 2, 3} \\ (i) {4 n | n \in X} = {4, 8, 12} (i i) {n + 6 | n \in X} = {7, 8, 9} \\ (i i i) {\frac{n}{2} | n \in X} = {\frac{1}{2}, 1, \frac{3}{2}} (i v) {(n - 1) | n \in X} = {0, 1, 2} \end{array}$

If Y = {1, 2, 3, ... 10}, and a represents any element of Y, write the following sets, containing all the elements satisfying the given conditions.

(i) a ∈ Y but a2 ∉ Y

(ii) a + 1 = 6, a ∈ Y

(iii) a is less than 6 and a ∈ Y

$\begin{array}{l} G i v e n t h a t : Y = {1, 2, 3, \dots, 10} \\ (i) {a \in Y b u t a^{2} \notin Y} = {4, 5, 6, 7, 8, 9, 10} \\ (i i) {a + 1 = 6, a \in Y} = {5} \\ (i i i) {a < 6 a n d a \in Y} = {1, 2, 3, 4, 5} \end{array}$

A, B and C are subsets of Universal Set U. If A = {2, 4, 6, 8, 12, 20}

B = {3, 6, 9, 12, 15}, C = {5, 10, 15, 20} and U is the set of all whole numbers, draw a Venn diagram showing the relation of U, A, B and C.

Kindly go through the solution

For all sets A, B and C, show that (A – B) ∩ (C – B) = A –(B ∪ C) .

$\begin{array}{l} T o p r o v e (A - B) \cap (A - C) = A - (B \cup C) \\ L . H . S . L e t x \in (A - B) \cap (A - C) \\ \Rightarrow x \in (A - B) a n d x \in (A - C) \\ \Rightarrow (x \in A a n d x \notin B) a n d (x \in A a n d x \notin C) \\ \Rightarrow x \in A a n d (x \notin B a n d x \notin C) \\ \Rightarrow x \in A - (B \cup C) \\ S o, (A - B) \cap (A - C) \subset A - (B \cup C) \dots (i) \\ R . H . S . L e t y \in A - (B \cup C) \\ \Rightarrow y \in A a n d y \notin (B \cup C) \\ \Rightarrow y \in A a n d (y \notin B a n d y \notin C) \\ \Rightarrow (y \in A a n d y \notin B) a n d (y \in A a n d y \notin C) \\ \Rightarrow y \in (A - B) a n d y \in (A - C) \\ S o, A - (B \cup C) \subset (A - B) \cap (A - C) \dots (i i) \\ F r o m e q . (i) a n d (i i), w e g e t \\ A - (B \cup C) = (A - B) \cap (A - C) \end{array}$

For all sets A and B, (A – B) ∪ (A ∩ B) = A

$\begin{array}{l} L . H . S . = (A - B) \cup (A \cap B) \\ = [(A - B) \cup A] \cap [(A - B) \cup B] \\ = A \cap (A \cup B) = A = R . H . S . \\ H e n c e, t h e g i v e n s t a t e m e n t i s' T r u e' . \end{array}$

For all sets A, B and C, if A ⊂ B, then A ∩ C ⊂ B ∩ C

$\begin{array}{l} L e t x \in A \cap C \\ \Rightarrow x \in A a n d x \in C \\ \Rightarrow x \in B a n d x \in C \\ \Rightarrow x \in (B \cap C) \Rightarrow (A \cap C) \subset (B \cap C) \\ H e n c e, t h e g i v e n s t a t e m e n t i s' T r u e' . \end{array}$

For all sets A, B and C, if A ⊂ B, then A ∪ C ⊂ B ∪ C

$\begin{array}{l} L e t x \in A \cup C \\ \Rightarrow x \in A o r x \in C \\ \Rightarrow x \in B o r x \in C [? A \subset B] \\ \Rightarrow x \in (B \cup C) \Rightarrow (A \cup C) \subset (B \cup C) \\ H e n c e, t h e g i v e n s t a t e m e n t i s' T r u e' . \end{array}$

For all sets A, B and C, if A ⊂ C and B ⊂ C, then A ∪ B ⊂C.

$\begin{array}{l} L e t x \in A \cup B \\ \Rightarrow x \in A o r x \in B \\ \Rightarrow x \in C o r x \in C [? A \subset C a n d B \subset C] \\ \Rightarrow x \in C \Rightarrow A \cup B \subset C \\ H e n c e, t h e g i v e n s t a t e m e n t i s' T r u e' . \end{array}$

For all sets A and B, A ∪ (B – A) = A ∪ B

$\begin{array}{l} L . H . S . = A \cup (B - A) = A \cup (B \cap A') [? A - B = A \cap B'] \\ = (A \cup B) \cap (A \cup A') \\ = A \cup B \cap U [? A \cup A' = U] \\ = A \cup B = R . H . S . [? A \cup U = A] \\ H e n c e, t h e g i v e n s t a t e m e n t i s p r o v e d . \end{array}$

For all sets A and B, A – (A – B) = A ∩ B

$\begin{array}{l} L . H . S . = A - (A - B) = A - (A \cap B') [? A - B = A \cap B'] \\ = A \cap (A \cap B') = A \cap [A' \cup (B')'] [? (A \cap B)' = A' \cup B'] \\ = A \cap [A' \cup B] [? (A')' = A] \\ = (A \cap A') \cup (A \cap B) = ? \cup (A \cap B) \\ = A \cap B = R . H . S . \\ H e n c e, t h e g i v e n s t a t e m e n t i s p r o v e d . \end{array}$

For all sets A and B, A – (A ∩ B) = A – B

$\begin{array}{l} L . H . S . = A - (A \cap B) = A \cap (A \cap B)' \\ = A \cap (A' \cup B') = (A \cap A') \cup (A \cap B') \\ = ? \cup (A - B) [? A - B = A \cap B'] \\ = A - B = R . H . S . \\ H e n c e, t h e g i v e n s t a t e m e n t i s p r o v e d . \end{array}$

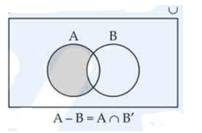
For all sets A and B, (A ∪ B) – B = A – B

$\begin{array}{l} L . H . S . = (A \cup B) - B = (A \cup B) \cap B' [? A - B = A \cap B'] \\ = (A \cap B') \cup (B \cap B') [? A \cap A' = ?] \\ = (A - B) \cup ? \\ = A - B = R . H . S . H e n c e p r o v e d . \end{array}$

Let T = xx + 5/x – 7 –5 = 4x – 40/13 – x. Is T an empty set? Justify your answer.

$\begin{array}{l} G i v e n t h a t : T = {x | \frac{x + 5}{x - 7} - 5 = \frac{4 x - 40}{13 - x}} \\ \Rightarrow \frac{x + 5}{x - 7} - 5 = \frac{4 x - 40}{13 - x} \\ \Rightarrow \frac{x + 5}{x - 7} - \frac{4 x - 40}{13 - x} = 5 \\ \Rightarrow \frac{(x + 5) (13 - x) - (x - 7) (4 x - 40)}{(x - 7) (13 - x)} = 5 \\ \Rightarrow \frac{13 x - x^{2} + 65 - 5 x - 4 x^{2} + 40 x + 28 x - 280}{13 x - x^{2} - 91 + 7 x} = 5 \\ \Rightarrow - 5 x^{2} + 76 x - 215 = 5 (13 x - x^{2} + 7 x - 91) \\ \Rightarrow - 5 x^{2} + 76 x - 215 = 65 x - 5 x^{2} + 35 x - 455 \\ \Rightarrow 76 x - 100 x = - 455 + 215 \\ \Rightarrow - 24 x = - 240 \Rightarrow x = \frac{240}{24} = 10 \\ ∴ T = 10 \\ H e n c e, T i s n o t a n e m p t y s e t . \end{array}$

Let A, B and C be sets. Then show that

A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

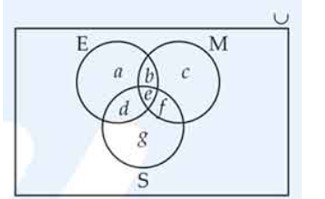
$\begin{array}{l} L e t x \in A \cap (B \cup C) \\ \Rightarrow x \in A a n d (x \in B o r x \in C) \\ \Rightarrow (x \in A a n d x \in B) o r (x \in A a n d x \in C) \\ \Rightarrow (x \in A \cap B) o r (x \in A \cap C) \\ \Rightarrow (x \in A \cap B) \cup (x \in A \cap C) \dots (i) \\ L e t y \in (x \in A \cap B) \cup (x \in A \cap C) \\ \Rightarrow y \in (x \in A \cap B) o r (x \in A \cap C) \\ \Rightarrow (y \in A a n d y \in B) o r (y \in A a n d y \in C) \\ \Rightarrow y \in A a n d (y \in B o r y \in C) \\ \Rightarrow y \in A a n d y \subset (B \cup C) \\ \Rightarrow y \in A \cap (B \cup C) \dots (i i) \\ F r o m e q (i) a n d (i i) w e g e t \\ A \cap (B \cup C) = (A \cap B) \cup (A \cap C) \\ L . H . S . = R . H . S . H e n c e p r o v e d . \end{array}$

Out of 100 students; 15 passed in English, 12 passed in Mathematics, 8 in science, 6 in English and Mathematics, 7 in Mathematics and Science; 4 in English and Science; 4 in all the three. Find how many passed

(a) In English and Mathematics but not in Science

(b) In Mathematics and Science but not in English

(c) In Mathematics only

(d) In more than one subject only

$\begin{array}{l} L e t t h e n u m b e r o f s t u d e n t s p a s s e d i n M a t h e m a t i c s M, E b e i n E n g l i s h a n d S b e i n S c i e n c e . \\ T h e n n (U) = 100, n (M) = 12, n (E) = 15, n (S) = 8 \\ n (E \cap M) = 6, n (M \cap S) = 7, n (E \cap S) = 4 a n d n (E \cap M \cap S) = 4 \\ L e t u s d r a w a v e n n d i a g r a m . A c c o r d i n g t o t h e v e n n d i a g r a m, w e g e t \\ a + b + d + e = 15 \dots (i) \\ b + c + e + f = 12 \dots (i i) \\ d + e + f + g = 8 \dots (i i i) \\ n (E \cap M) = 6 ∴ b + e = 6 \dots (i v) \\ n (M \cap S) = 7 ∴ e + f = 7 \dots (v) \\ n (E \cap S) = 4 ∴ d + e = 4 \dots (v i) \\ n (E \cap M \cap S) = 4 ∴ e = 4 \dots (v i i) \\ F r o m e q n . (i v) a n d (v i i) w e g e t b + 4 = 6 ∴ b = 2 \\ F r o m e q n . (v) a n d (v i i) w e g e t 4 + f = 7 ∴ f = 3 \\ F r o m e q n . (v i) a n d (v i i) w e g e t d + 4 = 4 ∴ d = 0 \\ F r o m e q n . (i) w e g e t a + b + d + e = 15 \\ \Rightarrow a + 2 + 0 + 4 = 15 \Rightarrow a = 9 \\ F r o m e q n . (i i) w e g e t b + c + e + f = 12 \\ \Rightarrow 2 + c + 4 + 3 = 12 \Rightarrow c = 3 \\ F r o m e q n . (i i i) w e g e t d + e + f + g = 8 \\ \Rightarrow 0 + 4 + 3 + g = 8 \Rightarrow g = 1 \\ ∴ (i) N u m b e r o f s t u d e n t s w h o p a s s e d i n E n g l i s h a n d M a t h e m a t i c s b u t n o t i n S c i e n c e, b = 2 \\ (i i) N u m b e r o f s t u d e n t s w h o p a s s e d i n M a t h e m a t i c s a n d S c i e n c e b u t n o t i n E n g l i s h, f = 3 \\ (i i i) N u m b e r o f s t u d e n t s w h o p a s s e d i n M a t h e m a t i c s o n l y, c = 3 . \end{array}$

In a class of 60 students, 25 students play cricket and 20 students play tennis, and10 students play both the games. Find the number of students who play neither?

$\begin{array}{l} T o t a l n u m b e r o f s t u d e n t s = 60 \Rightarrow n (U) = 60 \\ N u m b e r o f s t u d e n t s w h o p l a y C r i c k e t = 25 \Rightarrow n (C) = 25 \\ N u m b e r o f s t u d e n t s w h o p l a y T e n n i s = 20 \Rightarrow n (T) = 20 \\ N u m b e r o f s t u d e n t s w h o p l a y b o t h t h e g a m e s = 10 \Rightarrow n (C \cap T) = 10 \\ ∴ n (C \cup T) = n (C) + n (T) - n (C \cap T) \\ = 25 + 20 - 10 = 35 \\ N u m b e r o f s t u d e n t s w h o p l a y n e i t h e r = n (U) - n (C \cup T) \\ = 60 - 35 = 25 \end{array}$

In a survey of 200 students of a school, it was found that 120 study Mathematics, 90 study Physics and 70 study Chemistry, 40 study Mathematics and Physics, 30 study Physics and Chemistry, 50 study Chemistry and Mathematics and 20 none of these subjects. Find the number of students who study all the three subjects.

$\begin{array}{l} T o t a l n u m b e r o f s t u d e n t s = 200 \Rightarrow n (U) = 200 \\ N u m b e r o f s t u d e n t s w h o s t u d y M a t h e m a t i c s = 120 \Rightarrow n (M) = 120 \\ N u m b e r o f s t u d e n t s w h o s t u d y P h y s i c s = 90 \Rightarrow n (P) = 90 \\ N u m b e r o f s t u d e n t s w h o s t u d y C h e m i s t r y = 70 \Rightarrow n (C) = 70 \\ N u m b e r o f s t u d e n t s w h o s t u d y M a t h e m a t i c s a n d P h y s i c s = 40 \Rightarrow n (M \cap P) = 40 \\ N u m b e r o f s t u d e n t s w h o s t u d y P h y s i c s a n d C h e m i s t r y = 30 \Rightarrow n (P \cap C) = 30 \\ N u m b e r o f s t u d e n t s w h o s t u d y C h e m i s t r y a n d M a t h e m a t i c s = 50 \Rightarrow n (C \cap M) = 50 \\ N u m b e r o f s t u d e n t s w h o s t u d y n o n e o f t h e s u b j e c t s = 20 \Rightarrow n (M' \cap P' \cap C') = 20 \\ ∴ n (U) - n (M' \cap P' \cap C') = n (M \cup P \cup C) = 200 - 20 = 180 \\ N o w, n (M \cup P \cup C) = n (M) + n (P) + n (C) - n (M \cap P) - n (P \cap C) - n (C \cap M) + n (M \cap P \cap C) \\ \Rightarrow 180 = 120 + 90 + 70 - 40 - 30 - 50 + n (M \cap P \cap C) \\ \Rightarrow 180 - 160 = n (M \cap P \cap C) \\ \Rightarrow n (M \cap P \cap C) = 20 \\ H e n c e, t h e n u m b e r o f s t u d e n t s w h o s t u d y a l l t h e t h r e e s u b j e c t s = 20 . \end{array}$

In a town of 10,000 families it was found that 40% families buy newspaper A, 20% families buy newspaper B, 10% families buy newspaper C, 5% families buy A and B, 3% buy B and C and 4% buy A and C. If 2% families buy all the three newspapers. Find

(i) The number of families which buy newspaper A only.

(ii) The number of families which buy none of A, B and C

$\begin{array}{l} T o t a l n u m b e r o f f a m i l i e s = 10000 \Rightarrow n (U) = 10000 \\ N u m b e r o f f a m i l i e s w h o b u y N e w s p a p e r A = 40 % \Rightarrow n (A) = 40 % \\ N u m b e r o f f a m i l i e s w h o b u y N e w s p a p e r B = 20 % \Rightarrow n (B) = 20 % \\ N u m b e r o f f a m i l i e s w h o b u y N e w s p a p e r C = 10 % \Rightarrow n (C) = 10 % \\ N u m b e r o f f a m i l i e s w h o b u y N e w s p a p e r A a n d B = 5 % \Rightarrow n (A \cap B) = 5 % \\ N u m b e r o f f a m i l i e s w h o b u y N e w s p a p e r B a n d C = 3 % \Rightarrow n (B \cap C) = 3 % \\ N u m b e r o f f a m i l i e s w h o b u y N e w s p a p e r A a n d C = 4 % \Rightarrow n (A \cap C) = 4 % \\ N u m b e r o f f a m i l i e s w h o b u y a l l t h e t h r e e N e w s p a p e r s = 2 % \Rightarrow n (A \cap B \cap C) = 2 % \\ (i) N u m b e r o f f a m i l i e s w h o b u y N e w s p a p e r A o n l y \\ = n (A) - n (A \cap B) - n (A \cap C) + n (A \cap B \cap C) \\ \Rightarrow = \frac{40}{100} - \frac{5}{100} - \frac{4}{100} + \frac{2}{100} = \frac{33}{100} \\ \Rightarrow = 10000 \times \frac{33}{100} = 3300 f a m i l i e s \\ (i i) N u m b e r o f f a m i l i e s w h o b u y n o n e o f A, B a n d C \\ N e w s p a p e r i n p e r c e n t (%) = n (U) - n (A \cup B \cup C) \\ \Rightarrow n (U) - [n (A) + n (B) + n (C) - n (A \cap B) - n (B \cap C) - n (A \cap C) + n (A \cap B \cap C)] \\ \Rightarrow [100 - (40 + 20 + 10 - 5 - 3 - 4 + 2) %] \\ \Rightarrow (100 - 60) % = 40 % \\ ∴ N u m b e r o f f a m i l i e s w h o b u y n o n e o f A, B a n d C n e w s p a p e r o u t o f 10000 f a m i l i e s a r e \\ = 10000 \times \frac{40}{100} = 4000 f a m i l i e s . \end{array}$

In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:

French = 17, English = 13, Sanskrit = 15

French and English = 09, English and Sanskrit = 4

French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study

(i) French only

(ii) English only

(iii) Sanskrit only

(iv) French and English but not Sanskrit

(v) At least one of the three languages

(vi) English and Sanskrit

(vii) None of the three languages but not French

$\begin{array}{l} L e t u s u s e v e n n d i a g r a m m e t h o d . \\ T o t a l n u m b e r o f s t u d e n t s = 50 \Rightarrow n (U) = 50 \\ N u m b e r o f s t u d e n t s w h o s t u d y F r e n c h = 17 \Rightarrow n (F) = 17 \\ N u m b e r o f s t u d e n t s w h o s t u d y E n g l i s h = 17 \Rightarrow n (E) = 13 \\ N u m b e r o f s t u d e n t s w h o s t u d y S a n s k r i t = 15 \Rightarrow n (S) = 15 \\ N u m b e r o f s t u d e n t s w h o s t u d y F r e n c h a n d E n g l i s h = 9 \Rightarrow n (F \cap E) = 9 \\ N u m b e r o f s t u d e n t s w h o s t u d y E n g l i s h a n d S a n s k r i t = 4 \Rightarrow n (E \cap S) = 4 \\ N u m b e r o f s t u d e n t s w h o s t u d y F r e n c h a n d S a n s k r i t = 5 \Rightarrow n (F \cap S) = 5 \\ N u m b e r o f s t u d e n t s w h o s t u d y F r e n c h, E n g l i s h a n d S a n s k r i t = 3 \Rightarrow n (F \cap E \cap S) = 3 \\ n (F) = 17 \Rightarrow a + b + d + e = 17 \dots (i) \\ n (E) = 13 \Rightarrow b + c + e + f = 13 \dots (i i) \\ n (S) = 15 \Rightarrow d + e + f + g = 15 \dots (i i i) \\ n (F \cap E) = 9 ∴ b + e = 9 \dots (i v) \\ n (E \cap S) = 4 ∴ e + f = 4 \dots (v) \\ n (F \cap S) = 5 ∴ d + e = 5 \dots (v i) \\ n (E \cap F \cap S) = 3 ∴ e = 3 \dots (v i i) \\ F r o m e q n . (i v) b + 3 = 9 ∴ b = 6 \\ F r o m e q n . (v) 3 + f = 4 ∴ f = 1 \\ F r o m e q n . (v i) d + 3 = 5 ∴ d = 2 \\ F r o m e q n . (i) w e g e t a + 6 + 2 + 3 = 17 \Rightarrow a = 6 \\ F r o m e q n . (i i) w e g e t 6 + c + 3 + 1 = 13 \Rightarrow c = 3 \\ F r o m e q n . (i i i) w e g e t 2 + 3 + 1 + g = 15 \Rightarrow g = 9 \\ (i) N u m b e r o f s t u d e n t s w h o s t u d y F r e n c h o n l y, a = 6 \\ (i i) N u m b e r o f s t u d e n t s w h o s t u d y E n g l i s h o n l y, c = 3 . \\ (i i i) N u m b e r o f s t u d e n t s w h o s t u d y S a n s k r i t o n l y, g = 9 \\ (i v) N u m b e r o f s t u d e n t s w h o s t u d y E n g l i s h a n d S a n s k r i t b u t n o t F r e n c h, f = 1 . \\ (v) N u m b e r o f s t u d e n t s w h o s t u d y F r e n c h a n d S a n s k r i t b u t n o t E n g l i s h, d = 2 . \\ (v i) N u m b e r o f s t u d e n t s w h o s t u d y F r e n c h a n d E n g l i s h b u t n o t S a n s k r i t, b = 6 . \end{array}$

Sets Objective Type Questions

Suppose A₁, A₂, ..., A₃₀are thirty sets each having 5 elements and B₁, B₂, ..., B_nare n sets each with 3 elements, let =and each element of belongs to exactly 10 of the A_i’s and exactly 9 of the B,’S. Then n is equal to

(a) 15

(b) 3

(c) 45

(d) 35

Two finite sets have m and n elements. The number of subsets of the first set is112 more than that of the second set. The values of m and n are, respectively,

(a) 4, 7

(b) 7, 4

(c) 4, 4

(d) 7, 7

Commonly asked questions

(a) 15

(b) 3

(c) 45

(d) 35

$\begin{array}{l} N u m b e r o f e l e m e n t s i s A_{1} \cup A_{2} \cup A_{3} \dots \cup A_{30} \\ = 30 \times 5 = 150 (Repetition i s n o t d o n e) \\ B u t e a c h e l e m e n t i s u s e d 10 t i m e s \\ ∴ S = \frac{30 \times 5}{10} = 15 \\ I f t h e e l e m e n t s B_{1}, B_{2}, \dots, B_{n} a r e n o t r e p e a t e d . T h e n t h e t o t a l n u m b e r o f e l e m e n t s = 3 . \\ B u t e a c h e l e m e n t i s r e p e a t e d 9 t i m e s \\ ∴ S = \frac{3 n}{9} \Rightarrow 15 = \frac{n}{3} \Rightarrow n = 15 \times 3 = 45 \\ H e n c e, t h e c o r r e c t o p t i o n i s (c) . \end{array}$

Two finite sets have m and n elements. The number of subsets of the first set is112 more than that of the second set. The values of m and n are, respectively,

(a) 4, 7

(b) 7, 4

(c) 4, 4

(d) 7, 7

$\begin{array}{l} N u m b e r o f s u b s e t s o f a g i v e n s e t h a v i n g m e l e m e n t = 2^{m} a n d \\ t h e n u m b e r o f s u b s e t s o f s e t c o n t a i n i n g n e l e m e n t s = 2^{n} \\ A s p e r t h e g i v e n c o n d i t i o n, w e h a v e \\ 2^{m} - 2^{n} = 112 \\ \Rightarrow 2^{n} (2^{m - n} - 1) = 112 \Rightarrow 2^{n} . (2^{m - n} - 1) = 2^{4} . 7 \\ ∴ 2^{n} = 2^{4} a n d 2^{m - n} - 1 = 7 \\ \Rightarrow n = 4 a n d 2^{m - n} = 1 + 7 = 8 = 2^{3} \\ \Rightarrow n = 4 a n d m - n = 3 \Rightarrow m - 4 = 3 \Rightarrow m = 3 + 4 = 7 \\ H e n c e, t h e c o r r e c t o p t i o n i s (b) . \end{array}$

The set (A ∩ B′) ′ ∪ (B ∩ C) is equal to

(a) A′ ∪ B ∪ C (b) A′ ∪ B

(c) A′ ∪ C′ (d) A′ ∩ B

$\begin{array}{l} W e k n o w t h a t : (A \cap B)' = A' \cup B' \\ ∴ (A \cap B')' \cup (B \cap C) = [A' \cup (B')'] \cup (B \cap C) \\ = (A' \cup B) \cup (B \cap C) [? (B')' = B] \\ = A' \cup B \\ H e n c e, t h e c o r r e c t o p t i o n i s (b) . \end{array}$

Let F₁ be the set of parallelograms, F₂ the set of rectangles, F₃ the set of rhombuses, F₄the set of squares and F₅ the set of trapeziums in a plane. Then F₁may be equal to

(a) F₂ ∩ F₃

(b) F₃ ∩ F₄

(c) F₂ ∪ F₅

(d) F₂∪ F₃ ∪ F₄ ∪ F₁

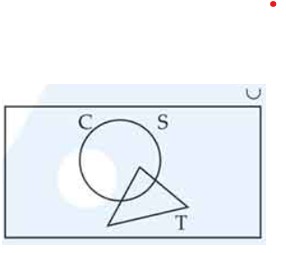
$\begin{array}{l} W e k n o w t h a t rectangles, rhombus a n d s q u a r e i n a p l a n e i s a parallelogram b u t t r a p e z i u m i s \\ n o t parallelogram . \\ ∴ F_{1} = F_{2} \cup F_{3} \cup F_{4} \cup F_{1} \\ H e n c e, t h e c o r r e c t o p t i o n i s (d) . \end{array}$

Let S = set of points inside the square, T = the set of points inside the triangle and C = the set of points inside the circle. If the triangle and circle intersect each other and are contained in a square. Then

(a) S ∩ T ∩ C = φ

(b) S ∪ T ∪ C = C

(c) S ∪ T ∪ C = S

(d) S ∪ T = S ∩ C

$\begin{array}{l} T h e g i v e n c o n d i t i o n s o f t h e q u e s t i o n m a y b e r e p r e s e n t e d b y t h e f o l l o w i n g V e n n d i a g r a m . \\ F r o m t h e g i v e n V e n n d i a g r a m, \\ W e c l e a r l y c o n c l u d e t h a t \\ S \cup T \cup C = s \\ H e n c e, t h e c o r r e c t o p t i o n i s (c) . \end{array}$

Let R be set of points inside a rectangle of sides a and b (a, b > 1) with two sides along the positive direction of x-axis and y-axis. Then

(a) R = {(x, y): 0 ≤ x ≤ a, 0 ≤ y ≤ b}

(b) R = {(x, y): 0 ≤ x < a, 0 ≤ y ≤ b}

(c) R = {(x, y): 0 ≤ x ≤ a, 0 < y < b}

(d) R = {(x, y): 0 < x < a, 0 < y < b}

Kindly go through the solution

In a class of 60 students, 25 students play cricket and 20 students play tennis, and 10 students play both the games. Then, the number of students who play neither is

(a) 0

(b) 25

(c) 35

(d) 45

$\begin{array}{l} T o t a l n u m b e r o f s t u d e n t s = 60 \Rightarrow n (U) = 60 \\ N u m b e r o f s t u d e n t s w h o p l a y C r i c k e t = 25 \Rightarrow n (C) = 25 \\ N u m b e r o f s t u d e n t s w h o p l a y T e n n i s = 20 \Rightarrow n (T) = 20 \\ N u m b e r o f s t u d e n t s w h o p l a y C r i c k e t a n d T e n n i s b o t h = 10 \\ \Rightarrow n (C \cap T) = 10 \\ ∴ n (C \cup T) = n (C) + n (T) - n (C \cap T) \\ = 25 + 20 - 10 = 45 - 10 = 35 \\ ∴ n (C' \cap T') = n (U) - n (C \cup T) \\ = 60 - 35 = 25 \\ H e n c e, t h e c o r r e c t o p t i o n i s (b) . \end{array}$

In a town of 840 persons, 450 persons read Hindi, 300 read English and 200 read both. Then the number of persons who read neither is

(a) 210

(b) 290

(c) 180

(d) 260

$\begin{array}{l} T o t a l n u m b e r o f p e r s o n s i n a t o w n = 840 \Rightarrow n (U) = 840 \\ N u m b e r o f p e r s o n s w h o r e a d H i n d i = 450 \Rightarrow n (H) = 450 \\ N u m b e r o f p e r s o n s w h o r e a d E n g l i s h = 300 \Rightarrow n (E) = 300 \\ N u m b e r o f p e r s o n s w h o r e a d b o t h = 200 \Rightarrow n (H \cap E) = 200 \\ ∴ n (H \cup E) = n (H) + n (E) - n (H \cap E) \\ = 450 + 300 - 200 = 550 \\ ∴ n (H' \cap E') = n (U) - n (H \cup E) \\ = 840 - 550 = 290 \\ H e n c e, t h e c o r r e c t o p t i o n i s (b) . \end{array}$

If X = {8n – 7n – 1 | n ∈ N} and Y = {49n – 49 | n ∈ N}. Then

(a) X ⊂ Y

(b) Y ⊂ X

(c) X = Y

(d) X ∩ Y = φ

$\begin{array}{l} G i v e n t h a t : X = {8^{n} - 7 n - 1 | n \in N} = {0, 49, 490, \dots} \\ Y = {49 n - 49 | n \in N} = {0, 49, 98, \dots} \\ H e r e, i t i s c l e a r t h a t e v e r y e l e m e n t b e l o n g i n g s t o X i s a l s o p r e s e n t i n Y . \\ ∴ X \subset Y . \\ H e n c e, t h e c o r r e c t o p t i o n i s (a) . \end{array}$

A survey shows that 63% of the people watch a News Channel whereas 76%watch another channel. If x% of the people watch both channels, then

(a) x = 35

(b) x = 63

(c) 39 ≤ x ≤ 63

(d) x = 39

$\begin{array}{l} L e t p % o f t h e p e o p l e w a t c h a c h a n n e l a n d q % o f t h e p e o p l e w a t c h a n o t h e r c h a n n e l \\ n (p \cap q) = x % a n d n (p \cup q) \leq 100 \\ n (p \cup q) \geq n (p) + n (q) - n (p \cap q) \\ 100 \geq 63 + 76 - x \Rightarrow 100 \geq 139 - x \\ x \geq 139 - 100 \Rightarrow x \geq 39 \\ N o w n (p) = 63 \\ ∴ n (p \cap q) \leq n (p) \Rightarrow x \leq 63 \\ S o, 39 \leq x \leq 63 \\ H e n c e, t h e c o r r e c t o p t i o n i s (c) . \end{array}$

If sets A and B are defined as

A = {(x, y) | y = 1/x, 0 ≠ x ∈ R} B = {(x, y) | y = – x, x ∈ R}, then

(a) A ∩ B = A

(b) A ∩ B = B

(c) A ∩ B = φ

(d) A ∪ B = A

$\begin{array}{l} G i v e n t h a t : A = {(x, y) | y = \frac{1}{x}, 0 \neq x \in R} \\ B = {(x, y) | y = - x, x \in R} \\ H e r e, i t i s c l e a r t h a t y = \frac{1}{x} a n d y = - x \\ ? \frac{1}{x} \neq - x \\ ∴ A \cap B = ? \\ H e n c e, t h e c o r r e c t o p t i o n i s (c) . \end{array}$

If A and B are two sets, then A ∩ (A ∪ B) equals

(a) A

(b) B

(c) φ

(d) A ∩ B

$\begin{array}{l} G i v e n t h a t : A \cap (A \cup B) \\ L e t x \in A \cap (A \cup B) \\ \Rightarrow x \in A a n d x \in (A \cup B) \\ \Rightarrow x \in A a n d (x \in A o r x \in B) \\ \Rightarrow (x \in A a n d x \in A) o r (x \in A a n d x \in B) \\ \Rightarrow x \in A o r x \in (A \cap B) \Rightarrow x \in A \\ H e n c e, t h e c o r r e c t o p t i o n i s (a) . \end{array}$

If A = {1, 3, 5, 7, 9, 11, 13, 15, 17} B = {2, 4, ..., 18} and N the set of natural numbers is the universal set, then A′ ∪(A ∪ B) ∩ B′) is

(a) φ

(b) N

(c) A

(d) B

$\begin{array}{l} G i v e n t h a t : A = {1, 3, 5, 7, 9, 11, 13, 15, 17} \\ B = {2, 4, \dots, 18} \\ U = N = {1, 2, 3, 4, 5, \dots} \\ A' \cup (A \cup B) \cap B' = A' \cup [(A \cap B') \cup (B \cap B')] \\ = A' \cup (A \cap B') \cup ? [? B \cap B' = ?] \\ = A' \cup (A \cap B') \\ = (A' \cup A) \cap (A' \cup B') \\ = N \cap (A' \cup B') [? A' \cup A = N] \\ = A' \cup B' = (A \cap B)' = (?)' = N [? A \cap B = ?] \\ H e n c e, t h e c o r r e c t o p t i o n i s (b) . \end{array}$

Let S = {x | x is a positive multiple of 3 less than 100}

P = {x | x is a prime number less than 20}. Then n(S) + n(P) is

(a) 34

(b) 31

(c) 33

(d) 30

$\begin{array}{l} G i v e n t h a t : S = {x | x i s a p o s i t i v e m u l t i p l e o f 3 < 100} \\ ∴ S = {3, 6, 9, 12, 15, 18, \dots, 99} \\ \Rightarrow n (S) = 33 \\ T = {x | x i s a p r i m e n u m b e r < 20} \\ ∴ T = {2, 3, 5, 7, 11, 13, 17, 19} \\ \Rightarrow n (T) = 8 \\ S o, n (S) + n (T) = 33 + 8 = 41 \\ H e n c e, t h e c o r r e c t o p t i o n i s (b) . \end{array}$

If X and Y are two sets and X′ denotes the complement of X, then X ∩ (X ∪ Y) ′is equal to

(a) X

(b) Y

(c) φ

(d) X ∩ Y

$\begin{array}{l} L e t x \in X \cap (X \cup Y)' \\ \Rightarrow x \in X \cap (X' \cap Y') \\ \Rightarrow x \in (X \cap X') \cap (X \cap Y') \\ \Rightarrow x \in ? \cap (X \cap Y') [? A \cap A' = ?] \\ \Rightarrow x \in ? \\ H e n c e, t h e c o r r e c t o p t i o n i s (c) . \end{array}$

Sets Fill in the blanks

The set {x ∈ R: 1 ≤ x < 2} can be written as ______________.

When A = φ, then number of elements in P(A) is ______________.

Commonly asked questions

The set {x ∈ R: 1 ≤ x < 2} can be written as ______________.

$\begin{array}{l} T h e s e t {x \in R : 1 \leq x < 2} c a n b e w r i t t e n a s [1, 2) \\ H e n c e, t h e f i l l e r i s [1, 2) . \end{array}$

When A = φ, then number of elements in P(A) is ______________.

$\begin{array}{l} H e r e, A = ? ∴ n (A) = 0 \\ ? n [P (A)] = 2^{n (A)} = 2^{0} = 1 \\ H e n c e, t h e f i l l e r i s 1 . \end{array}$

If A and B are finite sets such that A ⊂ B, then n (A ∪ B) = ______________.

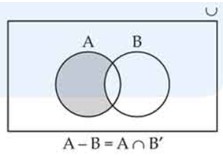
$\begin{array}{l} Since A \subset B ∴ n (A \cup B) = n (B) \\ H e n c e, t h e f i l l e r i s n (B) . \end{array}$

If A and B are any two sets, then A – B is equal to ______________.

$\begin{array}{l} F r o m t h e v e n n d i a g r a m i t i s c l e a r t h a t A - B = A \cap B' \\ H e n c e, t h e f i l l e r i s A \cap B' . \end{array}$

Power set of the set A = {1, 2} is ______________.

$\begin{array}{l} P o w e r s e t o f A = P (A) = {{1}, {2}, {1, 2}, ?} \\ H e n c e, t h e f i l l e r i s {{1}, {2}, {1, 2}, ?} . \end{array}$

Given the sets A = {1, 3, 5}. B = {2, 4, 6} and C = {0, 2, 4, 6, 8}. Then the universal set of all the three sets A, B and C can be ______________.

$\begin{array}{l} G i v e n t h a t : A = {1, 3, 5}, B = {2, 4, 6} a n d C = {0, 2, 4, 6, 8} \\ ∴ U n i v e r s a l s e t o f a l l t h e g i v e n s e t s i s \\ U = {0, 1, 2, 3, 4, 5, 6, 8} \\ H e n c e, t h e f i l l e r i s {0, 1, 2, 3, 4, 5, 6, 8} . \end{array}$

If U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, A = {1, 2, 3, 5}, B = {2, 4, 6, 7} and C = {2, 3, 4, 8}. Then

a) (B ∪ C) ′ is ______________.

b) (C – A) ′ is ______________.

$\begin{array}{l} G i v e n t h a t : U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} \\ A = {1, 2, 3, 5}, B = {2, 4, 6, 7} a n d C = {2, 3, 4, 8} \\ (i) (B \cup C)' = {2, 3, 4, 6, 7, 8}' = {1, 5, 9, 10} \\ H e n c e, t h e f i l l e r i s {1, 5, 9, 10} . \\ (i) (C - A)' = {4, 8}' = {1, 2, 3, 5, 6, 7, 9, 10} \\ H e n c e, t h e f i l l e r i s {1, 2, 3, 5, 6, 7, 9, 10} . \end{array}$

For all sets A and B, A – (A ∩ B) is equal to ______________.

^{$\begin{array}{l} Since A - B = A \cap B' \\ \Rightarrow A - (A \cap B) = A \cap B' \\ H e n c e, t h e f i l l e r i s A \cap B' . \end{array}$}

Match the following sets for all sets A, B and C

i. ((A′ ∪ B′) – A) ′ (a) A – B

ii. [B′ ∪ (B′ – A)] ′ (b) A

iii. (A – B) – (B – C) (c) B

iv. (A – B) ∩ (C – B) (d) (A × B) ∩ (A × C)

v. A × (B ∩ C) (e) (A × B) ∪ (A × C)

vi. A × (B ∪ C) (f) (A ∩ C) – B

$\begin{array}{l} (i) ((A' \cup B') - A)' = [(A' \cup B') \cap A']' [? A - B = A \cap B'] \\ = [(A \cap B)' \cap A']' [? A' \cup B' = (A \cap B)'] \\ = [(A \cap B)']' \cup (A')' [? (A')' = A] \\ = (A \cap B) \cup A = A . S o, (i) i s m a t c h e d w i t h (b) . \\ (i i) [B' \cup (B' - A)]' = [B' \cup (B' \cap A')]' [? A - B = A \cap B'] \\ = (B')' \cap (B' \cap A')' [? A' \cap B' = (A \cup B)'] \\ = B \cap (B \cup A) = B . S o, (i i) i s m a t c h e d w i t h (c) . \\ (i i i) (A - B) - (B - C) = (A \cap B') - (B \cap C') [? A - B = A \cap B'] \\ = (A \cap B') \cap (B \cap C')' \\ = (A \cap B') \cap (B' \cup (C')') [? A' \cup B' = (A \cap B)'] \\ = (A \cap B') \cap (B' \cup C) \\ = [A \cap (B' \cup C)] \cap [B' \cap (B' \cup C)] \\ = [A \cap (B' \cup C)] \cap B' \\ = (A \cap B') \cap (B' \cup C) \cap B' \\ = (A \cap B') \cap B' = (A \cap B') = A - B \\ S o, (i i i) i s m a t c h e d w i t h (a) . \\ (i v) (A - B) \cap (C - B) = (A \cap B') \cap (C \cap B') [? A - B = A \cap B'] \\ = (A \cap C) \cap B' = (A \cap C) - B [? A \cap B' = A - B] \\ S o, (i v) i s m a t c h e d w i t h (f) . \\ (v) A \times (B \cap C) = (A \times B) \cap (A \times C) \\ S o, (v) i s m a t c h e d w i t h (d) . \\ (v i) A \times (B \cup C) = (A \times B) \cup (A \times C) \\ S o, (v i) i s m a t c h e d w i t h (e) . \end{array}$

Maths NCERT Exemplar Solutions Class 11th Chapter One Exam

Student Forum

Anything you would want to ask experts?

Write here...

Other Similar chapters for you

Sets

News & Updates

Latest NewsPopular News

Maths NCERT Exemplar Solutions Class 11th Chapter One: Overview, Questions, Preparation

Sets Short Answer Type Questions

Commonly asked questions

Sets Objective Type Questions

Commonly asked questions

Sets Fill in the blanks

Commonly asked questions

Sets True and False Type Questions

Commonly asked questions

Try these practice questions

Student Forum

Other Similar chapters for you

News & Updates

CBSE Date Sheet 2026 Class 10, 12 (Final Out ) Live Updates; Download CBSE Exam Date Sheet PDF @cbse.nic.in

ICAI CA Result (Sept 2025) Live Updates: Check Time, Link, Process to Download (Foundation, Inter, Final)

JEE Main Marks vs Percentile vs Rank 2025: Calculate Percentile and Rank Using Marks

List of NIT Colleges in India 2025 - NIRF Ranking, Courses, Seats, Cutoff, Fees and Placement

CBSE 10th Maths Question Paper 2025, 2024, 2023, 2022, 2020, 2019 PDF Download

NEET Chapter Wise Weightage 2026 PDF by NTA: Physics, Chemistry & Biology

List of Top IITs in India 2025: NIRF Ranking, Courses, Seats, Fees & Placement