Kirchhoff's Law: Class 12 Physics Notes, Definition, Working Principle, Formula & Real-Life Applications

There are two types of Kirchhoff’s laws, including Kirchhoff's Law of Voltage (KVL) and Kirchhoff's Law of Current (KVL). The following table explains these two types of laws on the basis of different parameters

CBSE Board as well as other entrance examinations like NEET and JEE contain questions based on the NCERT concepts of Kirchhoff's law from current electricity chapter.

As per NCERT, Kirchhoff's law states that:

“Two rules, called Kirchhoff’s rules, are very useful for analysis of electric circuits. Given a circuit, we start by labelling currents in each resistor by a symbol, say I, and a directed arrow to indicate that a current I flows along the resistor in the direction indicated. If ultimately I is determined to be positive, the actual current in the resistor is in the direction of the arrow. If I turns out to be negative, the current actually flows in a direction opposite to the arrow. Similarly, for each source (i.e., cell or some other source of electrical power) the positive and negative electrodes are labelled, as well as, a directed arrow with a symbol for the current flowing through the cell. This will tell us the potential difference, V = V (P) – V (N) = e – I r [Eq. (3.38) between the positive terminal P and the negative terminal N; I here is the current flowing from N to P through the cell]. If, while labelling the current I through the cell one goes from P to N, then of course 

       V = e + I r                                                                                                                                                                                                                                                                                    (3.60)”

Having clarified labelling, we now state the rules and the proof: 

 

(Fig 3.15)

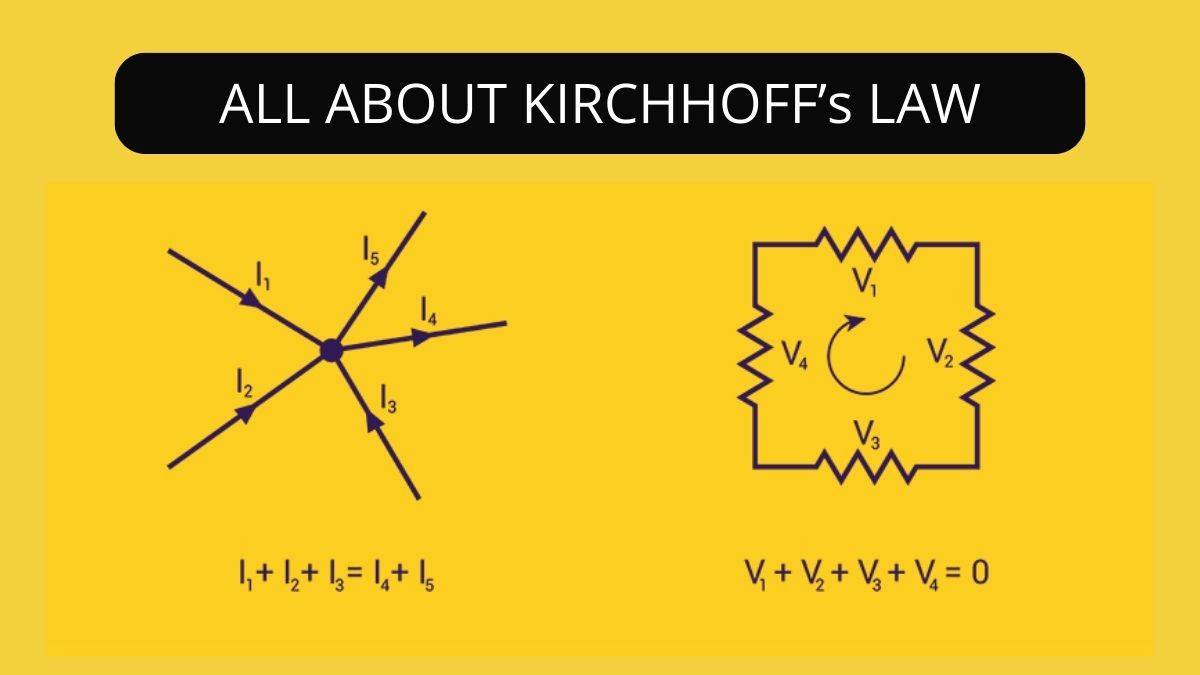
(a) Junction rule: At any junction, the sum of the currents entering the junction is equal to the sum of currents leaving the junction (Fig. 3.15). 

This applies equally well if instead of a junction of several lines, we consider a point in a line. The proof of this rule follows from the fact that when currents are steady, there is no accumulation of charges at any junction or at any point in a line. Thus, the total current flowing in, (which is the rate at which charge flows into the junction), must equal the total current flowing out. 

(b) Loop rule: The algebraic sum of changes in potential around any closed loop involving resistors and cells in the loop is zero (Fig. 3.15). 

This rule is also obvious, since electric potential is dependent on the location of the point. Thus, starting with any point if we come back to the same point, the total change must be zero. In a closed loop, we do come back to the starting point and hence the rule.”

There are two Kirchhoff’s laws, and both have been discussed below:

1. Kirchhoff's Current Law (Junction law)

Also known as Kirchhoff's first law, Kirchhoff’s law of current is based on the law of conservation of charge. It states, "The algebraic sum of the currents meeting at a point of the circuit is zero," or total currents entering a junction are equal to the total current leaving the junction.

$\underset{\text{in}}{\sum }I=\underset{\text{out}}{\sum }I$

The following Kirchhoff's Current Law diagram represents the Kirchhoff’s junction rule:

It is also known as Kirchhoff's current law (KCL).

2. Kirchhoff's Voltage Law (Loop law)

Also known as Kirchhoff's first law, it states that:

"The algebraic sum of all the potential differences along a closed loop is zero.
So IR + Σ  EMF = 0 ".
The closed loop can be traversed in any direction. While traversing a loop, if potential increases, put a positive sign in the expression, and if potential decreases, put a negative sign. (Assume sign convention)

Please note: It is important to understand mesh analysis since it is a circuit analysis method that systematically applies Kirchhoff's Voltage Law for writing loop equations for every mesh within the planar circuit. It also determines currents in the planar electrical network by assigning the mesh currents to meshes and creating equations for each based on KVL. Further, to become proficient in Kirchhoff's law formula and Kirchhoff's law example, one must practice Kirchhoff’s law problems provided in the NCERT solutions on current electricity chapter.

The working principle of Kirchhoff's laws works in the following manner:

• Kirchhoff's law of Current: This law applies conservation of charge to circuit junctions. Current law states that the sum of currents entering in a node is equal to the sum of currents that leaves the node. At any junction, current can neither be created nor destroyed. This maintains the charge balance.
• Kirchhoff's Law of Voltage (KVL): This law applies conservation of energy to closed loops. KVL requires the algebraic sum of all voltages around any closed loop to equal zero. This ensures energy balance is maintained throughout the circuit.
• Both these laws create mathematical relationships between circuit parameters. Engineers leverage these relationships to formulate equations to determine unknown values. Both Kirchhoff's laws apply universally to every electrical circuit, regardless of the complexity.
• Together, these laws provide a complete framework to analyze any electrical network.