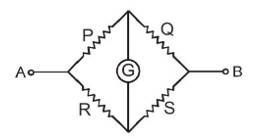
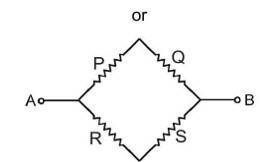
The Wheatstone bridge is a type of electrical circuit that measures unknown electrical resistance by balancing two legs of the bridge circuit. Amongst these two legs, one leg includes an unknown component called Rx. In 1833, Samuel Hunter Christie invented this bridge. It was later improved by Sir Charles Wheatstone in 1843.
Note: You can check out the NCERT solutions of Current Electricity chapter to learn more about the Wheatstone Bridge.
- What is Wheatstone Bridge?
- Different Types of Wheatstone Bridge Configurations
- Working Principle of Wheatstone Bridge
- Wheatstone Bridge Definition as Per NCERT
- Wheatstone Bridge Equation
What is Wheatstone Bridge?
WHEATSTONE NETWORK : (4 TERMINALNETWORK)
The arrangement as shown in the above diagram of Wheatstone bridge shows four terminals in which except two all are connected to each other through resistive elements. In this circuit if then and current in this is called balance point or null point. When current through the galvanometer is zero (null point or balance point) , then Here in this case products of opposite arms are equal. Potential difference between C and D at null point is zero. The null point is not affected by resistance and . It is not affected even if the positions of Galvanometer and battery ( ) are interchanged. Hence, here the circuit can be assumed to be following,
Different Types of Wheatstone Bridge Configurations
The following types of Wheatstone bridge configurations have been mentioned below:
| Type of Configurations |
Applications |
| Quarter Bridge |
Used when only one variable needs measurement |
| Half Bridge |
Provides improved temperature compensation and higher sensitivity |
| Full Bridge |
Offers maximum sensitivity and excellent temperature compensation |
| Maxwell Bridge |
For measuring inductance |
| Hay Bridge |
For measuring inductance with higher Q factors |
| Anderson Bridge |
For precise inductance measurements with better accuracy than Maxwell or Hay bridge |
| Schering Bridge |
For measuring capacitance and capacitor loss factors |
| Wien Bridge |
Used for frequency measurement applications and in oscillator circuits |
| Double Wheatstone Bridge |
For measuring very small resistances by eliminating contact and lead resistances |
| AC Bridges |
Operates with alternating current for measuring impedance, inductance, and capacitance |
Working Principle of Wheatstone Bridge
The Wheatstone bridge operates on a fundamental principle of electrical circuit comparison. Wheatstone bridge consists of four resistors arranged in a diamond pattern with a voltage source connected across one diagonal and a measurement device across the other. The circuit divides into two parallel voltage dividers:
- Left branch: R₁ and R₂ form one voltage divider
- Right branch: R₃ and R₄ form a second voltage divider
Balance Condition
The Wheatstone Bridge principle is the balance condition: when the ratio of resistances in the first branch equals the ratio in the second branch, the voltage difference across the measuring points becomes zero:
This is also the Wheatstone bridge formula. When this condition is met, the bridge is "balanced" and no current flows through the measuring device.
Measurement Mechanism
The working principle leverages this balance condition:
- In measurement applications, one or more resistors are replaced with sensors that change resistance in response to physical parameters.
- This change disrupts the balance.
- The resulting voltage across the measurement diagonal is proportional to the degree of imbalance.
- This voltage can be calibrated to the physical quantity being measured.
Wheatstone Bridge Definition as Per NCERT
As per NCERT, the Wheatstone bridge definition is as mentioned below:
“The Wheatstone bridge is an arrangement of four resistances – R1 , R2 , R3 , R4 as shown in the text. The null-point condition is given by:
using which the value of one resistance can be determined, knowing the other three resistances.”
Wheatstone Bridge Equation
This equation represents Wheatstone bridge formula which is the balance condition for a Wheatstone bridge circuit. When the ratio of the first two resistors (R₁/R₂) equals the ratio of the second two resistors (R₃/R₄), the bridge is "balanced."
- On the left side, R₁ is divided by R₂
- On the right side, R₃ is divided by R₄
- When these two ratios are equal, no current flows between the two branches
This balanced state is important because:
- It is the principle that allows the Wheatstone bridge to make precise measurements
- When balanced, the voltage difference across the measuring points is zero
- If any resistor value changes (like in a sensor application), the bridge becomes unbalanced, creating a voltage that can be measured
This simple relationship makes the Wheatstone bridge useful for detecting small changes in resistance, as the balance is very sensitive to even tiny variations in any of the four resistors.
Physics Current Electricity Exam
Student Forum
Other Topics under this Chapter
- Cells in Series and Parallel
- Kirchhoffs Law
- Ohms Law
- Wheatstone Bridge
- Overview
- Electric Current in Conductors
- Resistivity of a Material
- Limitations of Ohm's Law
- Electric Current
- Temperature Dependence of Resistivity
- Cells, EMF, Internal Resistance
- Electrical Energy and Power
- Drift of Electrons and the Origin of Resistivity
Other Class 12th Physics Chapters
- Physics Alternating Current
- Physics Ray Optics and Optical Instruments
- Physics Electromagnetic Induction
- Physics Dual Nature of Radiation and Matter
- Physics Semiconductor Devices
- Physics Wave Optics
- Physics Current Electricity
- Physics Nuclei
- Physics Electrostatic Potential and Capacitance
- Physics Atoms
- Physics Moving Charges and Magnetism
- NCERT Class 12 Notes
- NCERT Class 12 Physics
- Physics Electric Charge and Field
- Physics Electromagnetic Waves
- Physics Magnetism and Matter