Equations of Motion: Derivations, Applications, and How to Use

Kinematic equations are a set of formulas for describing the motion of an object in one dimension, i.e., a straight line. This object moves in constant or uniform acceleration. 

There are 3 kinematic equations for uniform accelerated motion.

1. v = v₀ + at 
2. x = v₀t + (1/2)at²
3. v² = v₀² + 2ax

These equations establish a relationship between five key variables: displacement (x), initial velocity (v₀), final velocity (v), acceleration (a), and time (t). 

The Key Condition: Uniform Acceleration

The main rule for the three kinematic equations to work or be applicable is to consider that the object moves in constant acceleration and in a single plane. 

If acceleration changes, the kinematic equations in most cases won’t be applicable.

Uniform accelerated motion refers to the motion of an object in a single plane or straight line where velocity changes in equal amounts and in equal time intervals. That makes acceleration constant or uniform.

One common example of uniform accelerated motion is gravity or the free fall of an object under its influence, considering we neglect air resistance. 

Till now, in early Class 11 chapters, we will consider idealised scenarios where air resistance or common forces in mechanics, such as friction, are negligible. In practical scenarios, true uniform accelerated motion is never fully achieved. But for using kinematic equations, this approximation of negligible forces makes it easier to understand them. 

 

The key to mastering the equations of motion is in being clear on the five main variables in uniformly accelerated motion. Some in Class 11 may directly confuse positive and negative directions for acceleration, velocity, or displacement, and misinterpret which value represents initial or final velocity. That could lead to choosing the wrong kinematic equation, or worse, not getting the right answers.  

Quantity	Symbol(s)	Definition
Displacement	s or Δx	Change in the position of the object.
Time	t	Duration over which motion takes place.
Initial Velocity	u or v₀	Speed and direction at the start of the motion.
Final Velocity	v	Speed and direction at the end of the time interval.
Constant or Uniform Acceleration	a	Steady rate of change of velocity.

 

The equations of motion with their derivations are below. For each, there are algebraic and calculus derivations. 

1st Equation of Motion Derivation: Velocity-Time Relation (v = v₀ + at)

This equation shows the relationship among four parameters in the uniformly accelerated motion of an object.

They are final velocity, initial velocity, acceleration, and time.

Algebraic Derivation of Velocity-Time Relation

This derivation comes directly from what you know of average acceleration:

a = (v - v₀) / (t - 0).

If we rearrange this, it gives us at = v - v₀, which leads to the final form.

Calculus Derivation of Velocity-Time Relation

We start with the definition a = dv/dt. Integrating dv = a dt (with a being constant) from the initial state (v₀ at t=0) to the final state (v at t) yields the equation.

So we use the integral symbol, ∫, which adds up the tiny pieces. With the sum of the infinitesimal velocity changes (dv) that happen during every single instant (dt), we can find the total.

∫ dv (from v₀ to v) = ∫ a dt (from 0 to t)

v - v₀ = at

v = v₀ + at

2nd Equation of Motion Derivation: Displacement-Time Relation

The second kinematic equation calculates displacement based on three parameters. They are initial velocity, time, and acceleration.

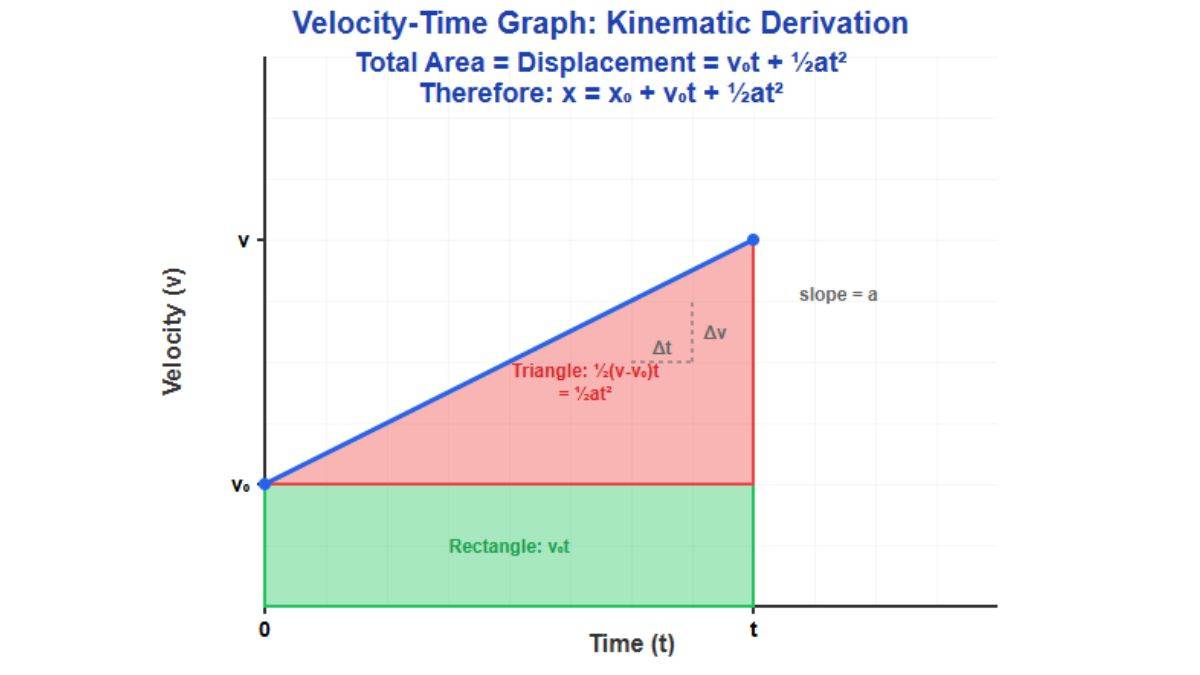
Graphical Derivation of Displacement-Time Relation

Let’s consider, displacement (x) is the area under a velocity-time (v-t) graph. 

For uniform acceleration, the graph is a straight line. 

The area under this line is a trapezoid. It can be split into a rectangle (area = v₀t) and a triangle (area = (1/2) * t * (v - v₀)). 

 

Since, we know, that v - v₀ = at, the total area is x = v₀t + (1/2)at²

Calculus Derivation for Displacement-Time Relation

Here, we are going to use the definition v = dx/dt. 

When we substitute the first kinematic equation, v = v₀ + at, it gives dx/dt = v₀ + at. 

Now when we integrate dx = (v₀ + at) dt from an initial position of 0 to x, we get the final equation.

It’s like this. We rearrange the equation to get all the position-related terms (dx) on one side. All the time-related terms (dt) are on the other side. dx = (v₀ + at) dt

Then we integrate both sides. The position is integrated from 0 to x. On the other hand, the time-dependent expression is integrated from 0 to t.

∫ (from 0 to x) dx = ∫ (from 0 to t) (v₀ + at) dt

The integral of dx is simply x.

Left Side: ∫ (from 0 to x) dx = [x] evaluated from 0 to x = (x) - (0) = x

Right Side: We can split the integral into two parts. Since v₀ and a are constants, we can take them out of their respective integrals.

∫ (v₀ + at) dt = ∫ v₀ dt + ∫ at dt

Solving each part using the power rule for integration (∫ tⁿ dt = tⁿ⁺¹ / (n+1)):

∫ v₀ dt = v₀t

∫ at dt = a ∫ t¹ dt = a * (t¹⁺¹ / (1+1)) = a * (t²/2) = (1/2)at²

Combining these gives: v₀t + (1/2)at²

3rd Equation of Motion Derivation: Velocity-Displacement Relation 

The third kinematic equation is useful when time (t) is unknown. 

It connects final velocity, initial velocity, acceleration, and displacement.

Substitution Derivation of Velocity-Displacement Relation

This equation can be derived by eliminating t from the first two equations. From v = v₀ + at, we get t = (v - v₀)/a. 

Substituting this into x = ((v + v₀)/2)t (another form of the displacement equation for constant a) gives the final result.

Calculus Derivation of Velocity-Displacement Relation 

Using the chain rule, a = dv/dt = (dv/dx) * (dx/dt) = v (dv/dx). 

Rearranging gives a dx = v dv. 

Integrating this from the initial state to the final state yields a(x) = (v² - v₀²)/2, which simplifies to the final equation.

What if an object does not start at the origin (x=0)?

You just have to include its initial position as, x₀. 

Then displacement x in all the 3 kinematic equations is replaced with the term (x - x₀).

v = v₀ + at (no change)

x = x₀ + v₀t + (1/2)at²

v² = v₀² + 2a(x - x₀)

Here are two simplified examples for the use cases of equations of motion, aligned to your NCERT syllabus. 

Free Fall in Gravity

One major application of kinematic equations is free fall. It’s the motion of an object solely under the influence of gravity.

Remember that free fall neglects air resistance in an ideal scenario of uniform accelerated motion. 

The acceleration is constant and directed downwards.

What happens to the acceleration (a) of the body? Well, it’s replaced by g, the acceleration due to gravity, which is approximately 9.8 m/s² near Earth's surface. 

The sign is typically negative (a = -g) if the upward direction is defined as positive.

Equations of Motion for Free Fall (from rest): If an object is dropped from rest (v₀=0) from a height y=0:

v = -gt

y = -(1/2)gt²

v² = -2gy

Note that height and rest are starting points.

Galileo's Law of Odd Numbers

Galileo's Law of Odd Numbers is a well-known principle in kinematics, which your textbook introduces. 

It states that an object falling from rest travels distances in equal time intervals. We will know that they are in the ratio of consecutive odd numbers (1:3:5:7...). 

Galileo provided the first quantitative proof that falling objects have uniform acceleration. 

Before calculus in maths, this work of Galileo established that the velocity of a falling body increases consistently over time. (You must also read Galileo's Law of Inertia, as through this empirical observation, we have Newton's Laws of Motion). 

This can be demonstrated using the kinematic equation y = (1/2)gt². 

For Kinematic equations Class 11-level questions, you can always refer to this table for quick reference. 

Kinematic Equation	Use When	Why	Example
v = v₀ + at	Displacement x is unknown	Solves for v,v₀,a, or t without x	Car accelerates from rest at 3 m/s² for 5 s — find v
x = v₀t +(1/2)at²	Final velocity v is unknown	Gives x using v₀,a,t, no need for v	Ball dropped from rest — find fall distance after 3 s
v² = v₀² + 2ax	Time t is unknown	Links v,v₀,a, and x without involving t	Car brakes from 20 m/s to stop over 50 m — find a