Functions in Math: Class 12 Maths Notes, Definition, Formula

Functions are everywhere in real life. For example:

1. The area of a circle depends on its radius: $A=\pi r^2$ . Here, $A$ is a function of $r$ .

2. The volume of a sphere depends on the radius: $\mathrm{V}=(4/3)\pi r^3$ .

3. Acceleration of an object depends on force applied and mass: a = F/m.

4. Taxi fare based on distance: If the base fare is $\mathrm{\$}10$ and the cost is $\mathrm{\$}2$ per mile, the total fare $F$ for $d$ miles is $F=10+2d$ .

Each of these scenarios shows how one quantity depends on another. This dependence is what we describe mathematically as a function.

“A relation f from a set A to a set B is said to be a function if every element of set A has one and only one image in set B.” In general, the definition of a function in maths is a rule that defines the relationship between inputs and outputs. 

A function is a relation between two sets. Let’s call them A and B. Every element that’s in Set A is called the domain. (The set of all inputs is the domain.) All these elements in Set A must be connected to one and only one element in Set B. (The set of outputs is the codomain.)

Simply put, when you write a function as a set of ordered pairs as (a, b), no two pairs can have the same first value. Then you will write the function as

f: A →B

Working example of a function in relation

A = {1, 2, 3}

B = {a, b, c}

f = {(1, a), (2, b), (3, c)}

Also, for a quick brush up, check the relations and functions overview.

A function is a relation of a special type that describes how an input can provide a unique output. In basic terms, a function is a rule that links each element of one set (called the domain) with exactly one element of another set (called the co-domain). If every input from the domain maps to only one output in the co-domain, we have a function. Mathematically, a function $f$  from set $A$ to set $B$  is written as:
f: $A\to B$

This means that for every $a$  in set $A$ , there is a corresponding $b$  in set $B$ , such that $f\left(a\right)=b$ . The output $b$ is known as the image of the input $a$ , and $a$ is the pre-image of $b$ .

Quick Explanation of a Function with an Example!

Think that you have a calculator that knows how to calculate the area of a square. 

So, 

• Input: You type the length of one side of the square into the calculator. It could be 5cm, let’s say. This is the input. 
• Rule: Now, this calculator has been programmed to multiply the input number by itself. As in, it performs 5cm x 5cm to calculate the area. That is, Area = side².
• Output: The calculator then shows the result as 25cm². This is the output. 

What makes it a function, then?

Whenever you enter 5 cm into this calculator, you will get the same result of 25 cm² again. The output will automatically (and always) depend on the input. This is because there is a specific formula to show the relationship between these two. 

If you change the number and the unit, the result will differ. For instance, you can choose 10m as the length of one side of the square. The area will then be Area = 10m x 10m = 100 m². As you can observe, the equation contains the rule of a function.

Also Read: Relations and Functions Class 12 Maths Solutions

History of Functions in Maths

Let’s look at some trivia on how functions came to be. 

Period	Key Figure(s)	Definition/Contribution
Pre-17th Century	Oresme, Galileo	Already known understanding of relationships between quantities; early examples of dependence and correspondence.
17th Century	Leibniz, Johann Bernoulli	Leibniz introduced the term "function" (initially geometric); Bernoulli defined it as a quantity formed from variables and constants.
18th Century	Leonhard Euler	Defined function as an "analytic expression"; made it central to analysis; introduced the notation f(x); later provided a more general definition.
Early 19th Century	Joseph Fourier	Claimed arbitrary functions could be represented by Fourier series, challenging the "analytic expression" definition.
Mid-19th Century	Nikolai Lobachevsky, Peter Gustav Lejeune Dirichlet	Independently provided a more general definition of a function as a relation where each input has a unique output, separating it from analytic expressions.
Late 19th Century	Richard Dedekind	Defined a function as a single-valued mapping between two sets.
20th Century	Nicolas Bourbaki	Formalised the set-theoretic definition, emphasising the unique association of each element in the domain with an element in the codomain.
20th Century	Saunders Mac Lane, et al.	Introduction and adoption of arrow notation (f: X → Y) to explicitly denote the domain and codomain of a function.

There are different types of functions based on how we map inputs and outputs. 

The major function types include the following. 

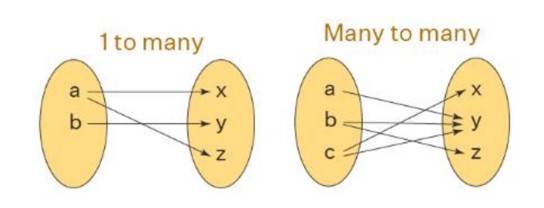
One-to-One Function (Injective): Each element in the domain maps to a unique element in the co-domain. No two inputs share the same output.

Example: f(x)=2x is one-to-one.

Many-to-One Function: Multiple inputs can have the same output.

Example: f(x)=x2 (since both 2 and -2 give the same output, 4).

Onto Function (Surjective): Every element in the co-domain is mapped by some element in the domain. That is, the range = co-domain.

Bijective Function: This is both one-to-one and onto. Every element in the domain maps to a unique element in the co-domain, and all co-domain elements are covered.

Mathematically, the function has the symbol f. It takes inputs from set A to produce outputs in set B. 

f : A → B

When we have an input a from the Domain A, and the function f maps it to an output b in the Codomain B, we write f(a) = b. A common way to write a function in mathematics is down here.  

f (x)=some expression involving x

Here,
f is the function’s name (you can also use g, h, etc.)

x is the input (from the domain)

f(x) is the output (in the codomain) - it’s what you get after applying the rule of the function to x

So, in algebra, when you see this equation f(x) = x²

• f is the function.

• x is any input from the Domain (i.e., the set of all real numbers).

• x² is the rule to find the output (the image).

• The output x² will be in the Range (which is [0, ∞) in this case) and also in the Codomain (which could also be real numbers).

This is a piecewise-defined function, meaning different rules apply based on the input value.

Function Name	Function Equation/Description	Graph Description/Behaviour
Identity Function	f(x) = x	A straight line passing through the origin. The output is always the same as the input.
Constant Function	f(x) = c	A horizontal line at the value of c. The output remains constant regardless of the input.
Rational Function	f(x) = 1/x	Has two curves in opposite quadrants that never touch the axes. It approaches zero as x increases and grows very large, near 0.
Modulus Function	f(x) = \	x\
Signum Function	Tells whether x is positive, negative, or zero.	Has three flat lines: at y = 1 for x > 0, y = -1 for x < 0, and y = 0 for x = 0.
Greatest Integer Function	Rounds down x to the nearest whole number, floor(x)	Creates a step-like pattern where the graph jumps at every integer value of x.