An object is in acceleration when its velocity changes. The rate at which velocity changes (rate of change of velocity) over time is called acceleration. An object accelerates when its velocity changes in one of three ways: increasing (which is what most people mean when they say acceleration), decreasing (also known as deceleration or retardation), or changing direction (also known as centripetal acceleration). Even if the traveling item did not accelerate or decelerate, a change in motion direction causes an acceleration.
This is due to the fact that acceleration is dependent on velocity change, and velocity is a vector quantity that has both magnitude and direction. Thus, the moon in orbit around the Earth accelerates, a car stops at a traffic light accelerates, and an apple falls. Any time an object changes direction or speeds up or down, it is said to be accelerating. Acceleration is the rate at which velocity changes over time.
- Acceleration Formula
- Average acceleration
- Types of Acceleration
- Equations Related to Acceleration
- Summary
Acceleration Formula
Average acceleration is the rate at which velocity changes:
where is average acceleration, v is velocity, and t is time. (The bar over the a means average acceleration.)
Because acceleration is velocity in meters divided by time in seconds, the SI unit of acceleration are often abbreviated -that is, meters per second squared or meters per second per second. This literally means by how many meters per second the velocity changes every second. Recall that velocity is a vector-it has both magnitude and directionwhich means that a change in velocity can be a change in magnitude (or speed), but it can also be a change in direction. For example, if a runner traveling at due east slows to a stop, reverses direction, continues her run at due west, her velocity has changed as a result of the change in direction, although the magnitude of the velocity is the same in both directions. Thus, acceleration occurs when velocity changes in magnitude (an increase or decrease in speed) or in direction, or both.
Average acceleration
Average acceleration is the rate at which velocity changes:
where is average acceleration, is velocity, and is time. (The bar over the means average acceleration.)
Because acceleration is velocity in meters divided by time in seconds, the SI units for acceleration are often abbreviated -that is, meters per second squared or meters per second per second. This literally means by how many meters per second the velocity changes every second. Recall that velocity is a vector-it has both magnitude and directionwhich means that a change in velocity can be a change in magnitude (or speed), but it can also be a change in direction. For example, if a runner traveling at due east slows to a stop, reverses direction, continues her run at due west, her velocity has changed as a result of the change in direction, although the magnitude of the velocity is the same in both directions. Thus, acceleration occurs when velocity changes in magnitude (an increase or decrease in speed) or in direction, or both.
Acceleration as a Vector
Acceleration is a vector in the same direction as the change in velocity, . Since velocity is a vector, it can change in magnitude or in direction, or both. Acceleration is, therefore, a change in speed or direction, or both.
Instantancous Acceleration
Instantaneous acceleration , or acceleration at a specific instant in time, is obtained using the same process discussed for instantaneous velocity. That is, we calculate the average velocity between two points in time separated by and let approach zero. The result is the derivative of the velocity function , which is instantaneous acceleration and is expressed mathematically as
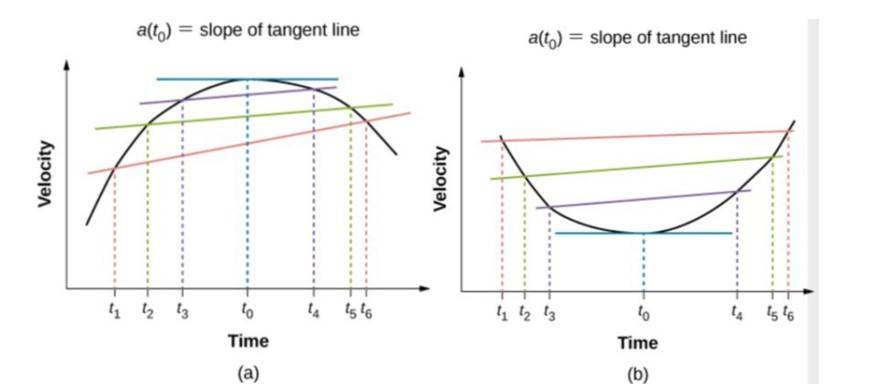
Thus, similar to velocity being the derivative of the position function, instantaneous acceleration is the derivative of the velocity function. We can show this graphically in the same way as instantaneous velocity. In Figure, instantaneous acceleration at time is the slope of the tangent line to the velocity-versus-time graph at time . We see that average acceleration approaches instantaneous acceleration as approaches zero. Also in part (a) of the figure, we see that velocity has a maximum when its slope is zero. This time corresponds to the zero of the acceleration function. In part (b), instantaneous acceleration at the minimum velocity is shown, which is also zero, since the slope of the curve is zero there, too. Thus, for a given velocity function, the zeros of the acceleration function give either the minimum or the maximum velocity.
Types of Acceleration
1. Uniform acceleration
Think of a skydiver falling: each second they pick up about the same extra speed—roughly 9.8 m/s more every second.
2. Non-uniform acceleration
In stop-and-go city traffic, your car speeds up and slows down at varying rates depending on lights and jams.
3. Centripetal acceleration
When you whirl a bucket on a rope, that steady inward tug keeping it moving in a circle is centripetal acceleration.
4. Tangential acceleration
Press the gas while turning a corner and the boost you feel along the arc is tangential acceleration.
5. Angular acceleration
Give a merry-go-round a push and watch how quickly its spin rate picks up—that change in rotation speed is angular acceleration.
Equations Related to Acceleration
1. First Equation of Motion
Acceleration is defined as
or
…..(1)
When time
, velocity
(say)
When time
, velocity
(say)
Integrating equation (1) within the above limits of time and velocity, we get
or
or
at …..(2)
2. Second Equation of Motion
Velocity is defined as
or
…..(3)
When time
, displacement travelled
When time
, displacement travelled
(say).
Integrating equation (3) within the above limits of time and distance, we get
or
or …..(4)
3. Third Equation of Motion
By the definitions of acceleration and velocity,
or ads
…..(5)
When time
, velocity
, displacement travelled
When time
, velocity
, displacement traveiled
(say)
Integrating equation (5) within the above limits of velocity and displacement, we get
or
or …..(6)
4. Fourth Equation of Motion
By definition of velocity,
…..(7)
When time second, displacement travelled
When time second, displacement
(say)
Integrating equation within the above limits of time and distance, we get
where displacement in second.
Summary
1. Acceleration is the rate at which velocity changes. Acceleration is a vector; it has both a magnitude and direction. The SI unit for acceleration is meters per second squared.
2. Acceleration can be caused by a change in the magnitude or the direction of the velocity, or both.
3. Instantaneous acceleration is a continuous function of time and gives the acceleration at any specific time during the motion. It is calculated from the derivative of the velocity function.
4. Instantaneous acceleration is the slope of the velocity-versus-time graph.
5. Negative acceleration (sometimes called deceleration) is acceleration in the negative direction in the chosen coordinate system.
Physics Motion in Straight Line Exam
Student Forum
Other Topics under this Chapter
Other Class 11th Physics Chapters
- Physics Mechanical Properties of Solids
- NCERT Class 11 Physics
- NCERT Class 11 Notes
- NCERT Notes
- Physics Motion in Plane
- Physics Mechanical Properties of Fluids
- Physics Motion in Straight Line
- Physics System of Particles and Rotational Motion
- Physics Oscillations
- Physics Waves
- Physics Thermal Properties of Matter
- Physics Motion
- Physics Gravitation
- Physics Thermodynamics
- Physics Work, Energy and Power
- Physics Units and Measurement
- Physics Laws of Motion