Refraction and Reflection of Plane Waves Using Huygens Principle: Check Examples & Working

Reflection and refraction are optical phenomena. Both describe how light interacts with interfaces between different media. 

Reflection is the bouncing back of light into the same medium after it strikes a surface. Based on Huygens Principle, the wavelets from the wavefront hit the surface and bounce off. The new wavefront is formed in a way that the reflection’s angle is the same as the angle of incidence.

Refraction is the bending of light as it passes from one medium to another. The Huygens Principle states that when light enters into a different medium, the speed of the wave changes. That’s how wavelets spread differently in the new medium. One part of the wavefront slows down or speeds up, and that causes light to bend, too. 

Importance of Refraction and Reflection of Plane Waves

• In JEE Exams, you can expect two to four questions on this chapter, where you may need to solve numerical problems based on these phenomena. 
• Engineering entrance exams usually focus on the applications bit, and might test your familiarity with the derivation of Snell’s Law. 

Huygens' construction, if modified a little, can help us understand the phenomena of reflection and refraction of light more. 

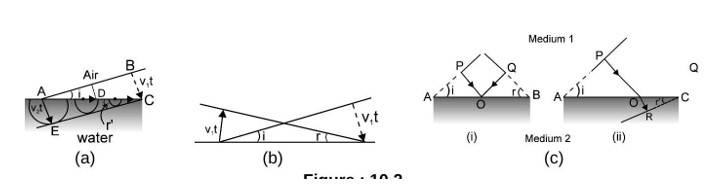
Figure (10.2a) shows an incident wavefront. It makes an angle ' $i$  ' with the surface that splits between water and air.

The phase speeds in air and water are ${\mathrm{v}}_1$ and ${\mathrm{v}}_2$ .

Now, when the point $A$ on the incident wavefront strikes the surface, the point $B$  still has to travel a distance $BC=AC\mathrm{s}\mathrm{i}\mathrm{n}i$ .

That takes the time, as we can see as $t=BC/v_1=AC(\mathrm{s}\mathrm{i}\mathrm{n}i)/v_1$ .

After the time $t$ , a secondary wavefront of radius ${\mathrm{V}}_2$ t with A as centre would have travelled into the second medium.

The secondary wavefront with C as centre would have just started, and has zero radius.

We also highlight a secondary wavelet that originates from a point $D$  in between $A$  and $C$ . The radius is less than $v_{2}t$ . So, medium 2's wavefront is a line that passes through $C$ and is tangent to the circle centred on $A$ .

We can observe that the angle $r^{\text{'}}$ that this refracted wavefront makes with the surface is  $AE=v_{2}t=AC\mathrm{s}\mathrm{i}\mathrm{n}{r}^{\text{'}}$ .

So, $t=AC\left(\mathrm{s}\mathrm{i}\mathrm{n}{r}^{\text{'}}\right\}/v_2$ .

When we equate the two expressions for ' $t$  ' ,we get the law of refraction in the form $\mathrm{s}\mathrm{i}\mathrm{n}i/\mathrm{s}\mathrm{i}\mathrm{n}r$ ' $=v_1/v_2$ .

Now, a similar picture is drawn in Fig. (10.2 b) for the reflected wave that travels back into medium 1. In this case, we denote the angle made by the reflected wavefront with the surface by and find that $i=r$ .

Note that for both reflection and refraction, we use secondary wavelets that start at different times.

You can also compare it with the earlier application (Fig.10.1) where we start them simultaneously.

The previous argument shows how the refracted and reflected waves are created from secondary wavelets.

That's how we also understand the laws of reflection and refraction with the concept that the time taken by light to travel along different rays from one wavefront to another must be the same.

(Fig. ) discusses the incident and reflected wavefronts when a parallel beam of light falls on a plane surface.

One ray POQ is seen as normal to both the reflected and incident wavefronts. The angle of incidence $i$  and the angle of reflection $r$ are defined as the angles made by the incident and reflected rays with the normal. As shown in Fig. (c), these are also the angles between the wavefront and the surface.

Figure : 10.2

(Fig.) (a) Huygens' construction for the (a) refracted wave. (b) Reflected wave. (c) Calculation of propagation time between wavefronts in (i) reflection and (ii) refraction.

Let's now calculate the total time to go from one wavefront to another along the rays. From Fig. (c), the Total time for light to reach from $P$ to $Q$

$=\frac{PO}{v_1}+\frac{OQ}{v_1}=\frac{AO\mathrm{s}\mathrm{i}\mathrm{n}i}{v_1}+\frac{OB\mathrm{s}\mathrm{i}\mathrm{n}r}{v_1}=\frac{OA\mathrm{s}\mathrm{i}\mathrm{n}i+(AB-OA)\mathrm{s}\mathrm{i}\mathrm{n}r}{v_1}=\frac{AB\mathrm{s}\mathrm{i}\mathrm{n}r+OA(\mathrm{s}\mathrm{i}\mathrm{n}i-\mathrm{s}\mathrm{i}\mathrm{n}r)}{v_1}$

Different rays normal to the incident wavefront strike the surface at different points $O$ .

That's why they have different values of OA.

Now, since the time should be the same for all the rays, the right side of the equation must actually be Independent of OA. The condition for this is that the coefficient of OA in Eq. (should be zero, i.e., $\mathrm{s}\mathrm{i}\mathrm{n}i=\mathrm{s}\mathrm{i}\mathrm{n}r$ . Then, we have the law of reflection, $i=r$ . Figure also shows refraction at a plane surface separating medium 1 (speed of light ${\mathrm{v}}_1$ ) from medium 2 (speed of light ${\mathrm{v}}_2$ ).

The incident and refracted wavefronts are shown, making angles $i$  and $r^{\text{'}}$  with the boundary. And, the angle $r^{\text{'}}$ is called the angle of refraction. We also draw rays perpendicular to these. As before, let us calculate the time taken to travel between the two wavefronts along any ray.
Time taken from P to $\mathrm{R}=\frac{\mathrm{P}\mathrm{O}}{{\mathrm{V}}_1}+\frac{\mathrm{O}\mathrm{R}}{{\mathrm{V}}_2}$

$=\frac{OA\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{i}}{v_1}+\frac{(AC-OA)\mathrm{s}\mathrm{i}\mathrm{n}{r}^{\text{'}}}{v_2}=\frac{AC\mathrm{s}\mathrm{i}\mathrm{n}{r}^{\text{'}}}{v_2}+OA\left(\frac{\mathrm{s}\mathrm{i}\mathrm{n}i}{v_1}-\frac{\mathrm{s}\mathrm{i}\mathrm{n}{r}^{\text{'}}}{v_2}\right)$

This time should again be independent of which ray we consider. The coefficient of $OA$ in Equation is, therefore, zero,. That is, $\frac{\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{i}}{\mathrm{s}\mathrm{i}\mathrm{n}{r}^{\text{'}}}=\frac{v_1}{v_2}=n_{21}$
where ${\mathrm{n}}_{21}$ is the refractive index of medium 2 with respect to medium 1. This is the Snell's law of refraction that we have already dealt with from Eq.

${\mathrm{n}}_{21}$  is the ratio of speed of light in the first medium $\left(v_1\right)$  to that in the second medium $\left(v_2\right)$ . The equation is Snell's law of refraction. With the first medium as vacuum, we have $\frac{\mathrm{s}\mathrm{i}\mathrm{n}i}{\mathrm{s}\mathrm{i}\mathrm{n}{r}^{\text{'}}}=\frac{c}{v_2}=n_2$
where ${\mathrm{n}}_2$

is the refractive index of medium 2 in relation to the vacuum. That is also called the absolute refractive index of the medium. 

We also have a similar equation that defines the absolute refractive index  $n_1$ of the first medium. From Eq. we then get ${\mathrm{n}}_{21}=\frac{{\mathrm{v}}_1}{{\mathrm{v}}_2}=\left(\frac{\mathrm{c}}{{\mathrm{n}}_1}\right)/\left(\frac{\mathrm{c}}{{\mathrm{n}}_2}\right)=\frac{{\mathrm{n}}_2}{{\mathrm{n}}_1}$
Air's absolute refractive index is close to 1.0003, quite close to 1 . So, the absolute refractive index of a medium could be taken with respect to air.

For water, ${\mathrm{n}}_1=1.33$ . That means ${\mathrm{v}}_1=\frac{\mathrm{C}}{1.33}$ . That is roughly around 0.75 times the speed of light in a vacuum. Foucault's measurement of light's speed in water in 1850 confirmed this prediction of the wave theory.

Explanation 

Once we know the laws of reflection and refraction, we can learn the behaviour of prisms, lenses, and mirrors. To explain the behaviour of the wavefronts in these three cases (Fig. 10.3)

• Suppose a plane wave passes through a thin prism. The portion of the incoming wavefront travelling through the most significant glass thickness gets the most delayed. As light travels much slower in glass, we understand why there is a tilt in the emerging wavefront.
• Likewise, the central part of an incident plane wave traverses the thickest portion of a convex lens and is most delayed. The emerging wavefront will have a depression at the centre. It is spherical and converges to a focus.
• A concave mirror, on the other hand, creates a similar effect. The centre of the wavefront must travel a greater distance before and after being reflected than the edge, again producing a converging spherical wavefront.
• Lenses and mirrors make light from an object arrive at the image at the same time. For instance, when a convex lens focuses light to form a real image, the rays going through the centre are shorter. But light goes slower in glass. It will take the same time for a ray going through a thicker centre and going out through a thinner edge

Figure: 10.3

• Formation of images by mirrors in everyday life.
• Vision: The lens in our eye refracts light to form an image on the retina.
• Rainbows: Caused by refraction, dispersion, and reflection of sunlight in raindrops.
• Optical fibers only use total internal reflection to transmit light signals.