What is the Equation of A Circle: Its Derivation and Forms

The equation of circle is x² + y² + 2gx + 2fy + c = 0, where center of the circle is at point (-g, -f) and radius is given by formula r = √(g² + f² - c). 

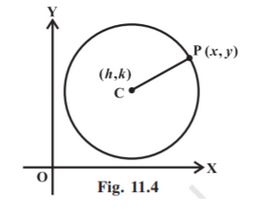
Let the centre of the circle be at a fixed point C (h, k) and the length of the radius be equal to r. If P(x, y) be the moving point on the circle, we have the definition | CP| = r. Therefore, the equation is: 

$$\begin{gathered} \sqrt{{(x-h)}^2+{(y-k)}^2}=r \\ {}^{} \end{gathered}$$

$${(x-h)}^2+{(y-k)}^2=r^2$$

Class 12th students who are going to take CBSE board exams must be well aware of the concept to perform well in the exam.

Some Particular Cases

• If the centre is at the origin and the radius r, then h = 0, k=0, and the equation of the circle is x²+y² = r². This is called the standard form of the equation of a circle.
• If the origin lies on the circle, then h²+k² = r², and so the equation of the circle in this case is x²+y² -2hx -2ky = 0.
• If the centre lies on the x-axis, then the centre’s ordinate is zero, i.e. k=0, and so the equation of the circle is (x-h)² + y² = r².

This is an important topic from Conic Sections, which covers different forms of the equation of a circle. Amongst them, the general form of circle's equation is as follows:

• The general equation of the circle is given by x² + y² + 2gx + 2fy + c = 0, where g, f and c are constants.
• The centre of this circle is ( - g, -f )
• The radius of the circle is √(g²+ f² -c)
• The general equation of a circle passing through the origin is given by x²+y² -2gx -2fy = 0.

Let us discuss different forms of equation of circle one by one:

1· Standard (centre–radius) form

${(x-h)}^2+{(y-k)}^2=r^2$

Centre = (h, k) and radius = r. If h = k = 0, it reduces to $x^2+y^2=r^2$.

2· General quadratic form

$x^2+y^2+2gx+2fy+c=0$

Centre = (−g, −f); radius =  $\sqrt{g^2+f^2-c}$.

3· Intercept (axis-touching) form

$x^2+y^2-ax-by=0$

Touches the x-axis at (a, 0) and the y-axis at (0, b). Radius = ½√(a² + b²).

4· Diameter form (end-points known)

$(x-x_1)(x-x_2)+(y-y_1)(y-y_2)=0$

Works because any angle in a semicircle is 90°, so the product of slopes is −1.

5· Parametric form

$x=h+r\cos \theta ,y=k+r\sin \theta ,0\le \theta <\mathrm{2\pi }$

Single parameter θ (0 → 2π) traces the whole circle; great for calculus or plotting.

6· Tangent-normal form at point (x₁, y₁)

$x{x}_1+y{y}_1=r^2$

This is the tangent to a circle centred at the origin. (The normal line joins the centre to (x₁, y₁).)

7 · Concentric-family form

$x^2+y^2+2gx+2fy+k=0$

Changing k changes the radius but keeps the centre fixed at (−g, −f).

1: Equation of the circle whose centre is at ( -5, 4) and the radius is 7 is –

Solution. (x+5)2 + (y-4)2 = 72

i.e., x2+ y2+ 10x - 8y- 8 = 0.

2. Find the centre and the radius of the circle x² + y²+ 8x + 10y – 8 = 0.

Solution. The given equation is (x² + 8x) + (y² + 10y) = 8

Now, completing the squares within the parenthesis, 

we get (x²+ 8x + 16) + (y² + 10y + 25) = 8 + 16 + 25 i.e. (x + 4)² + (y + 5)² = 49 i.e. {x – (– 4)}² + {y – (–5)}² = 72.

Therefore, the given circle has a centre at (– 4, –5) and radius 7.

Questions based on the steps of the derivation are often asked in entrance exams such as JEE Main and IIT JAM. Here, we will be sharing the step-by-step derivation of circle's equation:

1. Standard (centre–radius) form

$${(x-h)}^2+{(y-k)}^2=r^2$$

Centre = (h, k), radius = r. If h = k = 0 you get $x^2+y^2=r^2$.

2. General quadratic form

$$x^2+y^2+2gx+2fy+c=0$$

Centre = (−g, −f); radius = $\sqrt{g^2+f^2-c}$.

3. Intercept (axis-touching) form

$$x^2+y^2-ax-by=0$$

Touches x-axis at (a, 0) and y-axis at (0, b). Radius = ½√(a² + b²).

4. Diameter form (end-points known)

$$(x-x_1)(x-x_2)+(y-y_1)(y-y_2)=0$$

Valid because any angle in a semicircle is 90°.

5. Parametric form

$$x=h+r\cos \theta ,y=k+r\sin \theta ,0\le \theta <\mathrm{2\pi }$$

One parameter θ sweeps out the entire circle—ideal for calculus or plotting.

6. Tangent–normal form at a point (x₁, y₁)

$$x{x}_1+y{y}_1=r^2$$

This is the tangent to (x − h)² + (y − k)² = r² when the circle is centred at the origin.

7. Concentric-family form

$$x^2+y^2+2gx+2fy+k=0$$

Different values of k yield circles with the same centre (−g, −f) but varying radii.