Area Under Simple Curves: Overview, Questions, Preparation

The "area under a simple curve" refers to the area enclosed by a curve (represented by a function f(x)), the x-axis, and two vertical lines representing the limits of an interval [a, b]. It's a concept in calculus that quantifies the accumulation of a quantity (represented by the function) over that specific interval. 

Integrals have a wide range of applications in various disciplines like science, engineering, etc. We have already discussed that definite integration can be used to determine the area between a curve and the x-axis. We shall use definite integration to find the area under simple curves like lines, circles, parabolas, ellipses, and the area bounded by any two of the said curves.

Conclusion:

• The area between the curves y = f(x) and y = g(x) such that f(x) ≥ g(x) on [a, b] is given by

Area =  ${\int }_a^b\left[f\left(x\right)-g\left(x\right)\right]dx$  = ${\int }_a^b\left[Uppercurvefunction-Lowercurvefunction\right]dx$

• The area between the curves x = f(y) and x = g(y) such that f(y) ≥ g(y) on [c, d] is given by

Area = ${\int }_c^d\left[f\left(y\right)-g\left(y\right)\right]dy$    = ${\int }_c^d\left[Rightcurvefunction-Leftcurvefunction\right]dy$

 

We shall discuss the area problems in which we are given a single curve whose equation contains both x and y.

Important Topics:

NCERT Class 11 notes	CBSE NCERT Class 11 Physics
Class 11 Chemistry notes	Class 11 Maths notes

Working Rules for Area Under Simple Curves

• Identify the curves and interval
  • First of all, you have to write the equation of the curve (e.g. y = f(x)).
  • Now decide the interval [a,b] along the axis (x-axis or y-axis) over which you have to find the area.
• Check the curve position
  • The area is positive if the curve is above the x-axis.
  • The integral's value is negative if the curve is below the x-axis. The curves crossing the x-axis break the interval into parts and are calculated separately.
• Apply the integration method
  • For the curve y = f (x):

Area = ${\int }_a^{b}f\left(x\right)dx$

• • For a curve g = f(y)

Area = ${\int }_c^{d}g\left(y\right)dy$

Area between two curves:

• If a region is bounded between two curves, $y_1=f_1\left(x\right)\text{and}{y}_2=f_2\left(x\right)$ then:

Area = ${\int }_a^b\left[f_1\left(x\right)-f_2\left(x\right)\right]dx$

Use symmetry when possible
In case the curve is symmetrical about x-axis or y-axis, calculate the area of one part and multiply accordingly. This will make the calculation easy.

Example: Find the area of the region bounded by the line 2y = – x + 8, the x–axis and the lines x = 2 and x = 4.

Solution: Given curves are

              (i) 2y = – x + 8 (i.e., y = $-\frac{x}{2}$  + 4)             (ii) x – axis (i.e., y = 0)

              (iii) x = 2                                                        (iv) x = 4

 

Shading the required region:

              y = $-\frac{x}{2}$  + 4                                      y = 0, x = 2, x = 4

             

x	0	8	2	4
y	4	0	3	2

 

Hence, required area = ${\int }_2^4\left[\left(-\frac{x}{2}+4\right)-0\right]dx$

    = ${\left[\frac{-x^2}{4}+4x\right]}_2^4$ = (– 4 + 16) – (– 1 + 8) = 5 sq. units.

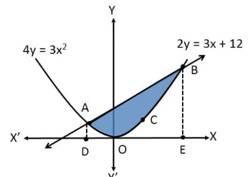
Example: Find the area enclosed by the parabola 4y = 3x² and the line 2y = 3x + 12.

Solution: Given curves are

 

              (i) 4y = 3x² (i.e., y = $\frac{{3x}^2}{4}$ )           (ii) 2y = 3x + 12 (i.e., y = $\frac{3x}{2}$  + 6)

From (i) and (ii), we have

       $\frac{{3x}^2}{4}$         = $\frac{3x}{2}$ + 6    $\Rightarrow$    x² = 2x + 8   $\Rightarrow$ x² – 2x – 8 = 0    $\Rightarrow$      x = 4, – 2

Curves (i) and (ii) intersect each other at (4, 12) and (– 2, 3).

Shading the required region:

                             y =        $\frac{{3x}^2}{4}$                        y = $\frac{3x}{2}$  + 6

x	0	4	– 2
y	0	12	3

x	0	– 4	4	– 2
y	6	0	12	3

 

Hence, required area = ${\int }_{-2}^4\left[\left(\frac{3x}{2}+6\right)-\frac{{3x}^2}{4}\right]dx$

   = ${\left[\frac{3x^2}{4}+6x-\frac{x^3}{4}\right]}_{-2}^4$

= (12 + 24 – 16) – (3 – 12 + 2) = 27 sq. units.

The area under the curve is calculated using the following steps:

1. Know the equation of the curve y=f(x), limits, and the axis enclosing the area. 
2. Find the integration (antiderivative) of the curve.
3. Finally, apply the upper limit and lower limit to the integral and find the difference to obtain the area under the curve.

$Area={\int \; <!--\; \int \; -->}_a^{b}y.dx$

= ${}_a{\int \; <!--\; \int \; -->}^{b}f(x).dx$

= $[g(x){]}_a^b$

= $g(b)-\; <!--\; -\; -->g(a)$

Also Read: NCERT Notes for Class 11 & 12

While preparing for the board exam or the entrance examination, students must focus on a few points that will make it easier to solve the problems based on the area under the curves. Below are the key points to remember.

Working rule

• Express the equations of the given curves in the form y = f(x).
• Find the point(s) of intersection of the curves.
• Sketch the region whose area is to be determined. It can be done as follows:
  • Draw tables for both the equations containing the values of x and the corresponding values of y. The values in the table can be specifically chosen as x = 0, y = 0 and given values of x and y (if any) and point(s) of intersection. To know the shape of the curve more accurately, we can also take some more values of x and y.
  • Plot the points (x, y) using a table and join them smoothly to get the required curve.
  • Draw the given values of x (if any) as the lines parallel to the y-axis.
  • Draw the given values of y (if any) as the lines parallel to the x-axis.
  • Colour or darken the region satisfying all the conditions of the given problem.
• To find the required area, use the formula

Area = ${\int }_a^b\left[Uppercurvefunction-Lowercurvefunction\right]dx$

 

Students can find here complete notes for CBSE Class 12 Maths.

Chapter No.	Chapter Notes
1	Relations and Functions
2	Inverse Trigonometric Functions
3	Matrices
4	Determinants
5	Continuity and Differentiability
6	Application of Derivatives
7	Integrals
8	Application of Integrals
9	Differential Equations
10	Vector Algebra
11	Three-Dimensional Geometry
12	Linear Programming
13	Probability

Preparation for the exam is an important task that every student must follow. To prepare, it is important to have proper study materials. Here we have provided the link for Clas 12 Maths solutions.

S.No.	Name of Chapter
1	Chapter 1 Relations and Functions
2	Chapter 2 Inverse Trigonometric Functions
3	Chapter 3 Matrices
4	Chapter 4 Determinants
5	Chapter 5 Continuity and Differentiability
6	Chapter 6 Applications of Derivatives
7	Chapter 7 Integrals
8	Chapter 8 Application of Integrals
9	Chapter 9 Differential Equations
10	Chapter 10 Vector Algebra
11	Chapter 11 Three-Dimensional Geometry
12	Chapter 12 Linear Programming
13	Chapter 13 Probability