The early 20th century saw way too many scientific discoveries. The Rutherford scattering experiment is among the most well-known.
In Class 12 Physics, you already know the basics of atoms. It’s time to see how experiments like Rutherford’s laid the groundwork for the future of physics in the time we are living today.
With Hans Geiger and Ernst Marsden, Rutherford set up this gold foil experiment.
The conclusions from the calculations radically changed what the world previously misunderstood about atoms.
- What is the Rutherford Scattering Experiment?
- How Did Rutherford Scattering Experiment Disprove the Thomson Model?
- Alpha Particle Scattering Experiment Setup
- Observations of the Alpha Scattering Experiment
- Rutherford’s Nuclear Model of the Atom
- Rutherford Scattering Formula and Theory
- Rutherford’s Atomic Model in Comparison with Thomson's Model
- Rutherford's Atomic Model Limitations
- Modern Applications of Rutherford's Atomic Model
- Revise Physics Notes for Class 12 NCERT
- Practice NCERT Solutions Class 12
What is the Rutherford Scattering Experiment?
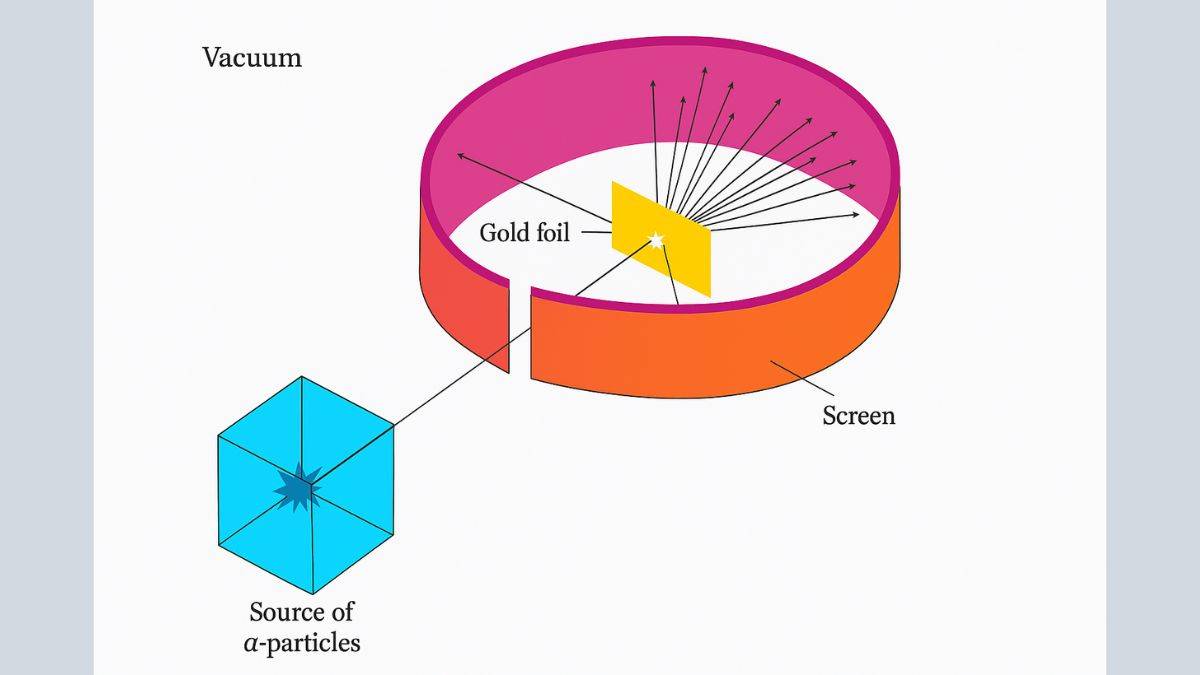
The Rutherford scattering experiment involved firing a beam of positive alpha particles at a thin sheet of gold foil. This was to test Thomson's observation of subatomic particles, where the apparatus comprised of an α-source, gold foil, and ZnS screen. Most particles passed through undeflected, a few deflected at small angles, and very few, bounced back. The conclusions Rutherford and team came to were that every atom has a tiny nucleus at its centre, where most mass is concentrated. And electrons orbit the nucleus, like planets around the sun. But the limitation of this Rutherford nuclear model was to identify atomic stability and spectra.
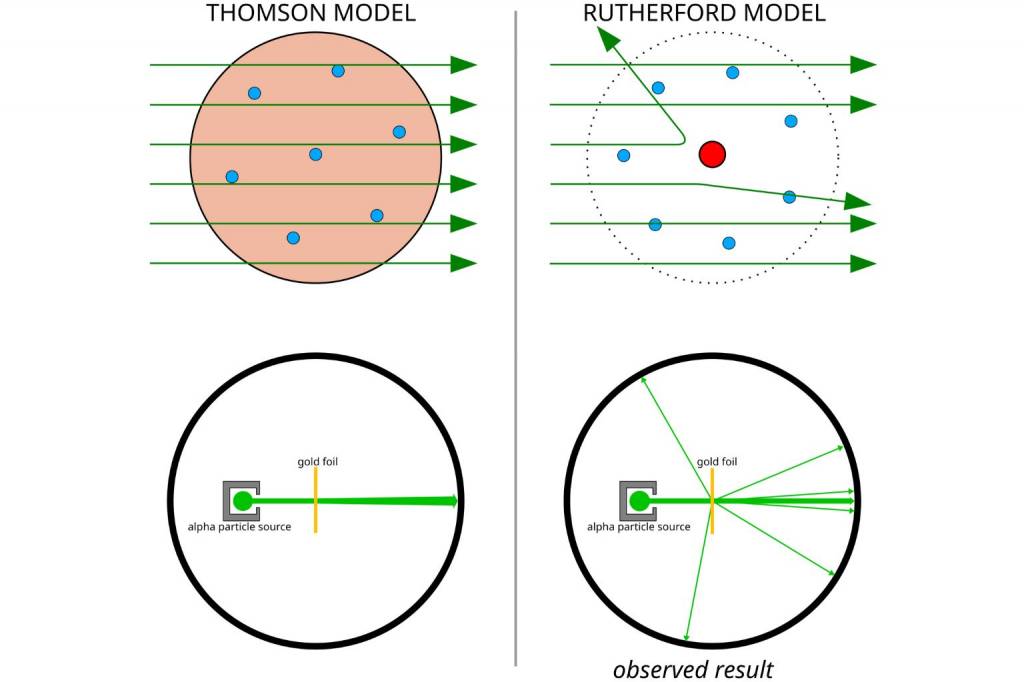
How Did Rutherford Scattering Experiment Disprove the Thomson Model?
You may recall from Class 11 chemistry about Thomson’s Plum Pudding Model.
This view proposed that an atom was a sphere with a positive charge spread evenly.
Here, electrons with negative charge would exist as blobs, more like raisins in a pudding.
But this idea was a fail, when the alpha particle scattering experiment was carried out.
Rutherford, in his experiment with Geiger and Marsden, thought about it like this.
If Thomson’s plum pudding model were correct, the spread-out positive charge inside an atom wouldn’t have enough pull to push around a heavy alpha particle.
So, when he and his team fired a beam of alpha particles at a thin sheet of gold foil, he expected almost all of them to sail straight through.
Maybe a tiny wobble here and there.
But Rutherford’s experiment saw sharp deflections. Some particles even bounced back. This scientific observation totally went against what Thomson had suggested.
That also provided enough scientific evidence that electrons are not placed within the nucleus but orbit around it.
A bit about Rutherford, the father of nuclear physics
- Ernest Rutherford (1871-1937) was a New Zealand-born British physicist.
- Before his famous alpha particle scattering experiment, he had already established himself as a pioneer in radioactivity research.
- Having discovered alpha and beta rays, he developed the modern theory of radioactivity with fellow scientist Frederick Soddy. His work on the scattering of alpha particles from metal foils would soon reveal the true structure of the atom.
- With nuclear scientist Ernest Rutherford, we have Hans Geiger and Ernst Marsden. All of them carried out this alpha particle scattering experiment (in fact, a series of them) between 1908/1909 and 1911. The conclusions of the Rutherford alpha particle scattering experiment were published in 1911. Even students would later go on to publish more about the apparatus and process used for alpha scattering.
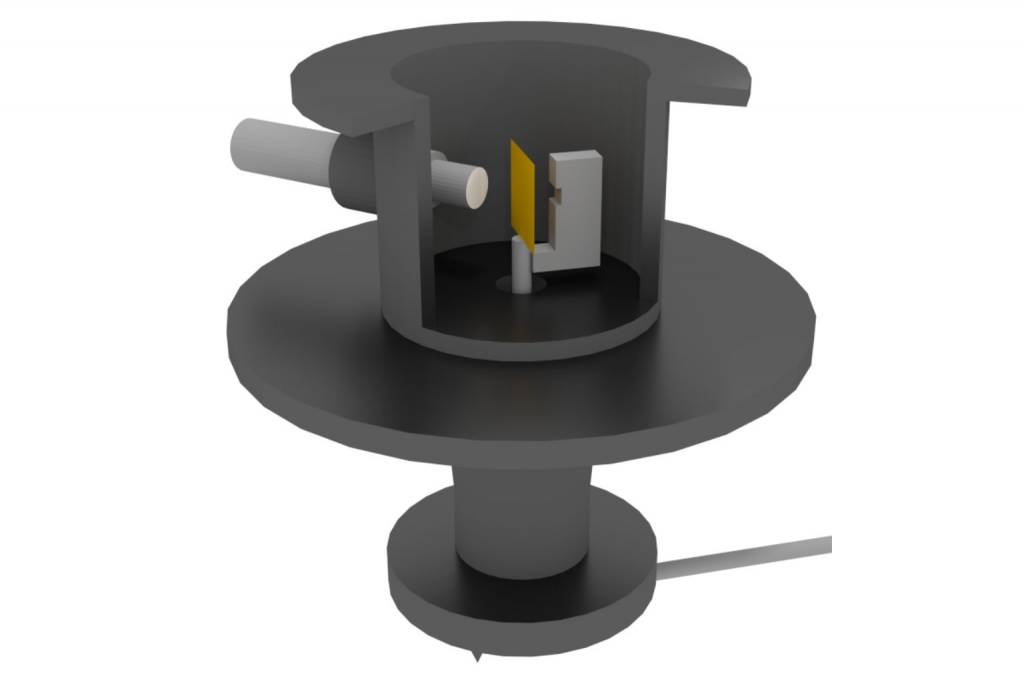
Alpha Particle Scattering Experiment Setup
Let’s now examine the experiment setup that Rutherford and his team conducted.
Design and Apparatus with Rutherford and Team
Their experimental apparatus had the following.
- Radioactive Source: A ²¹⁴₈₃Bi (Bismuth-214) source emitting 5.5 MeV alpha particles.
- Collimator: Lead bricks for creating a narrow, focused beam of alpha particles.
- Target: An extremely thin gold foil with a thickness of 2.1 × 10⁻⁷ m.
- Detector: Rotating detector with ZnS Screen was coupled with a microscope. This screen is also referred to as the scintillation screen.
- Vacuum Chamber: The entire apparatus was an enclosure to prevent air interference.
Rutherford’s detector used a ZnS screen, where alpha particles produced tiny flashes called scintillations.
These were counted under a microscope to measure scattering angles.
Why Gold Foil for Alpha Particle Scattering?
The gold foil in the Rutherford alpha scattering experiment was essential for these reasons.
- Gold is quite malleable. It can be hammered into thin sheets.
- It has a high atomic number (Z = 79). This, in fact, provided strong electromagnetic interactions.
- Gold doesn't react with air. That’s how it is convenient to maintain experimental consistency.
- The foil could be made thin enough (only a few hundred atoms thick) so they could minimise multiple scattering events.
Observations of the Alpha Scattering Experiment
Let’s look at how the results of Rutherford's experiment created an impact in the scientific world.
Results of the Alpha Scattering Experiment
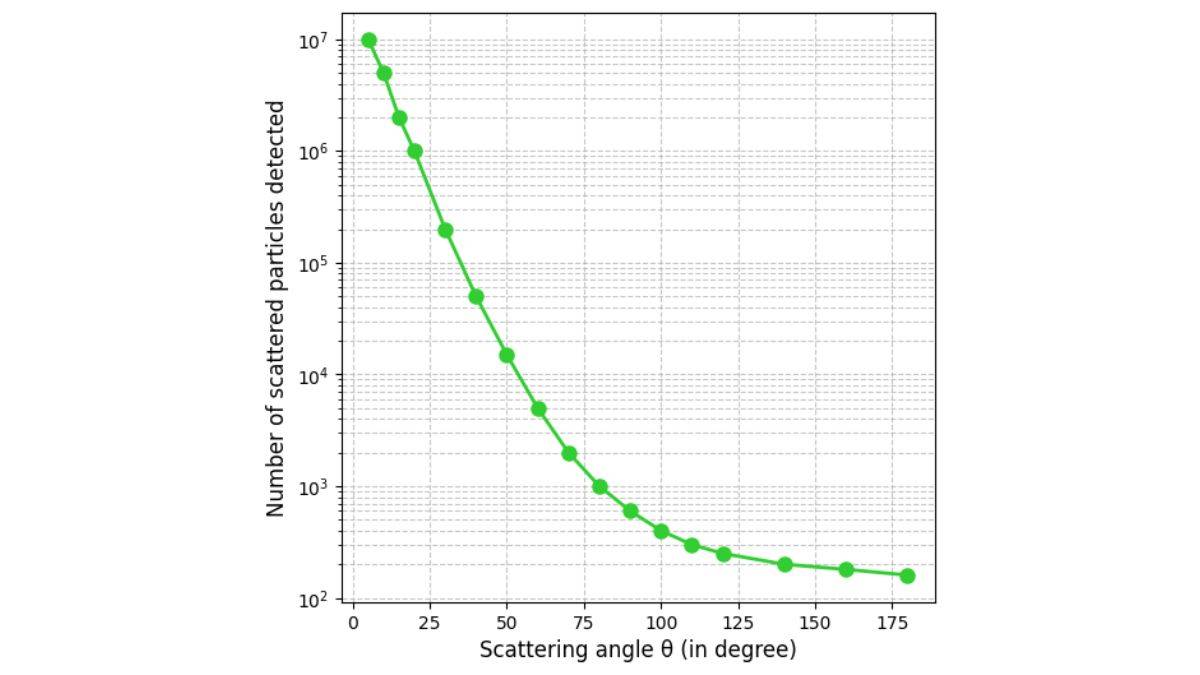
The scattering of alpha particles by gold foil led to three important observations that primarily challenged the Thomson Plum Pudding Model.
- Most alpha particles passed straight through the foil. There were no deflections at all.
- Approximately 0.14% of incident alpha particles are scattered by more than 1°.
- About 1 in 8000 alpha particles deflected by more than 90° (some even bounced straight back).
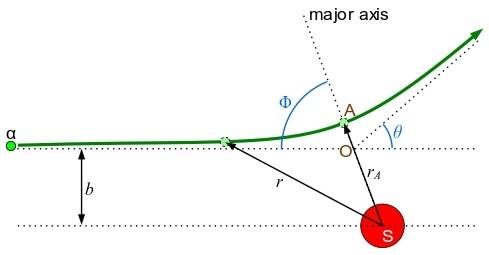
Path of the Particle: Trajectory and Impact Parameters
The alpha particle trajectory is heavily dependent on the impact parameter.
The impact parameter is basically the perpendicular distance between the initial path of the alpha particle and the centre of the target nucleus. We denote it by the letter b.
Quick tip: The impact parameter is the ‘aim’ of the alpha particle.
Mathematical Relationship Between Alpha Particle Trajectories and Impact Parameter
- A small impact parameter (b) will have a large scattering angle (θ). This is a close encounter. That means, when an alpha particle is aimed too close to a nucleus, it will have a small impact parameter. Here, we have to consider that both the alpha particle and the nucleus are positively charged. Because of that, a strong repulsive force will begin. That causes a particle to be deflected at a large angle.
- A large impact parameter (b) will have a slight scattering angle (θ). This is the opposite situation. Here we need to think of the alpha particle to be aimed far away from at the nucleus so that it has a large impact parameter. The repulsive force it is going to experience would be pretty much weaker. It would continue on its path without deviating much. That will lead to a small amount of deflection.
- Head-on collision (b ≈ 0) will create a phenomenon known as backscattering (θ ≈ 180°). This is an extreme and rare case. The alpha particle is aimed directly at the nucleus. The impact parameter is going to be close to zero. You see this because the alpha particle would slow down. It will stop and then rebound back on the same path it took. So the scattering angle comes quite close to 180 degrees.
Rutherford’s Nuclear Model of the Atom
Previously, we studied that Thomson’s plum pudding model had failed to explain the results of the alpha particle scattering experiment. This led Rutherford to develop a new theory in 1911 that clearly explained the structure of the atom.
Based on this alpha particle experiment, he jumped to the following conclusions. These are also known as the postulates of Rutherford experiment.
- There is a small, dense and positively charged nucleus at the centre of the atom (only this could cause the deflection).
- The nucleus comprises the atom’s majority mass, and is extremely small compared to the atom.
- Negatively charged electrons revolve around the nucleus of the atom in circular, and an atom’s majority space is empty.
This marked the end of Thomson's plum pudding model and contributed to the development of the modern quantum mechanical model. That was initiated by Niels Bohr, another student of Rutherford.
Either way, this concept of the nucleus introduced by this theory laid the foundation of all atomic theories in the upcoming years.
The nuclear model of the atom came from Rutherford’s conclusions on the alpha particle scattering experiment.
Conclusions of the Alpha Particle Scattering Experiment
Rutherford's analysis of the experimental data led to a radical reinterpretation of atomic structure.
The Rutherford atomic model conclusion mentioned
- The atom is mostly empty space. That explains why most alpha particles pass through undeflected.
- All positive charge and most mass are concentrated in a tiny nucleus at the centre.
- Electrons orbit the nucleus like planets around the sun. The planetary model, that is.
Calculating Nuclear Dimensions
From the alpha particle scattering experiment data, Rutherford was able to estimate the nuclear dimensions.
Nuclear radius: ~10⁻¹⁵ to 10⁻¹⁴ m
Atomic radius: ~10⁻¹⁰ m
This means the nucleus is approximately 10,000 to 100,000 times smaller than the atom itself. This is what Class 12 Physics NCERT book section 12.2 mentions.
Let’s put that in some real-life perspective.
If you were to scale up an atom to the size of a large football stadium, the nucleus would be no bigger than a marble sitting in the centre of the field.
This also disproves the Thomson atomic model. It implies that most of an atom is empty space.
Distance of Closest Approach Calculation
As earlier we got to know about those rare head-on collisions, we can calculate just how close the alpha particle gets to the nucleus before it turns back.
This is the distance of closest approach (d).
It's calculated using a fundamental principle that you may recall from previous physics studies. The conservation of energy.
As the alpha particle speeds towards the nucleus, it has kinetic energy (the energy of motion). As it gets closer, the electrostatic repulsion from the nucleus slows it down. It converts its kinetic energy into electric potential energy.
At the very point it stops and turns around, all of its initial kinetic energy has been transformed into potential energy.e
So, we can set up a simple equation as
Initial Kinetic Energy (K) = Final Electric Potential Energy (U)
Let’s take a deeper look at this equation.
The initial kinetic energy is K.
The charge of an alpha particle is 2e. That’s a helium nucleus with two protons.
The charge of the target nucleus is Ze. Z is the atomic number. It also is the number of protons in the nucleus.
Now, from previous chapters, we know the electric potential energy between two charges has the formula
(1 / 4πε₀) × (q₁q₂ / r)
Now we substitute these values into the conservation of energy equation.
K = (1 / 4πε₀) × ( (2e)(Ze) / d )
It simplifies to
K = (1 / 4πε₀) × ( 2Ze² / d )
We could also rearrange this formula, to find the distance of closest approach (d).
d = (1 / 4πε₀) × ( 2Ze² / K )
Try this textbook-style example of a numerical problem
For a 7.7 MeV alpha particle hitting gold (Z = 79).
d = (2)(9.0 × 10⁹)(1.6 × 10⁻¹⁹)²(79) / (1.2 × 10⁻¹²)
d = 3.0 × 10⁻¹⁴ m = 30 femtometres
Since 1 femtometre (fm) is 10⁻¹⁵ meters, this distance is 30 fm.
What does this distance really tell us?
This calculated distance of closest approach is like an approximation. It tells us the upper limit for the size of the nucleus. That means we can’t know the exact size of the nucleus from this specific calculation. But what we do know for sure is that it cannot be any bigger than this value.
In the above example, it proves that the radius of the gold nucleus must be less than 3.0 × 10⁻¹⁴ metres or 30 fm.
This result means that the alpha particle never actually touches the nucleus. The repulsive force is so strong that it reverses the particle's course at a distance that is still considerably larger than the combined radii of the gold nucleus and the alpha particle itself.
It's like two powerful magnets repelling each other before they can make contact.
Rutherford Scattering Formula and Theory
The Scattering Cross-Section
The Rutherford scattering formula describes the probability of scattering at different angles.
dσ/dΩ = (Z₁Z₂e²/4πε₀)² × (1/4E)² × (1/sin⁴(θ/2))
Where:
- dσ/dΩ is the differential cross-section
- Z₁, Z₂ are the atomic numbers of the projectile and the target
- E is the kinetic energy of the incident particle
- θ is the scattering angle
Force Analysis
The mathematical way of understanding the alpha particle scattering experiment is further understood through the repulsive Coulomb force between the alpha particle and the nucleus. That is,
F = (1/4πε₀) × (2e × Ze)/r²
This force:
- Acts along the line that connects the alpha particle and the nucleus
- Continuously changes magnitude and direction during the encounter
- Provides the deflecting force responsible for scattering
Explanation
From the above, we can say that the entire scattering phenomenon in Rutherford's experiment is because of the Coulomb force. It’s the force of repulsion between two objects with the same type of charge. Both are positive, just remember that for clarity.
The two key players here are
- The incoming alpha-particle. This has a positive charge of 2e
- The stationary nucleus of the gold atom, which has a much larger positive charge of Ze. Recall Z is the atomic number and it’s 79 for gold.
And if you backtrack a little, the Coulomb force operates under an inverse square law.
That just means the force gets exponentially stronger as the distance between the two particles shrinks. Visualise it as a protective bubble around the nucleus.
When an alpha particle is far away, the Coulomb force is next to nothing. The particle travels in a straight line.
The moment it gets closer, it begins to feel the repulsive push. If its initial path is far from the nucleus, it has a large impact parameter.
So it only feels the weak and that too, the outer edges of this force field and is only slightly deflected.
But when the alpha-particle is on a path with a small impact parameter, it travels deep into the region where the Coulomb force is quite powerful.
This intense, close-range repulsion is what causes the particle to be deflected at a large angle, or even sent straight back.
So, it's this continuously changing Coulomb force. That is, the inverse square law tells us that it deflects the alpha-particle. The particle's final trajectory is a direct consequence of its impact parameter. This indicates just how deep into this powerful repulsive field it goes into.
This relationship between the calculated trajectories and the observed results is what gave Rutherford's nuclear model its incredible predictive power.
Rutherford’s Atomic Model in Comparison with Thomson's Model
Here, the focus is on the discovery of the nature of electrons, as per the model of Rutherford.
To recap, we can see that Rutherford experiment disproved Thomson's plum pudding model in the following way.
| Thomson's Model |
Experimental Observation |
| Thomson had considered a uniform charge distribution |
Large-angle scattering observed, and that practically questioned how would there be any uniform charge that would be distributed evenly |
| The Plum Pudding Model did not consider any concentrated mass |
There was backscattering of alpha particles, which implied that there would be a place in the atom where mass is concentrated |
| Small deflections were expected but no so much in reality |
1 in 8000 particles deflected at angles above 90 degrees |
Electron Orbits in Rutherford's Model
In the Rutherford nuclear model, electrons maintain stable orbits through:
Electrostatic attraction = Centripetal force
(1/4πε₀) × e²/r² = mv²/r
This leads to the mathematical observation
- Kinetic energy: K = e²/(8πε₀r)
- Potential energy: U = -e²/(4πε₀r)
- Total energy: E = -e²/(8πε₀r)
The negative total energy indicates that electrons are bound to the nucleus.
Rutherford's Atomic Model Limitations
Modern Applications of Rutherford's Atomic Model
Revise Physics Notes for Class 12 NCERT
Practice NCERT Solutions Class 12
Commonly asked questions
Why couldn’t Rutherford explain the stability of an atom?
Based on what classical electromagnetic theory says, we know that an accelerated charged particle must radiate energy or electromagnetic waves. That remains continuous.
By looking at the Rutherford’s atomic model we can assume that electrons would revolve around the nucleus, which in this logic, held in orbit by electrostatic attraction. The reason is that, their path is circular that’s always accelerating. That would mean the electron would start to lose energy and finally let the atom to implode. But that doesn’t happen. Atoms are stable and that’s where classical physics that led to Rutherford model failed.
How did Rutherford know that an atom was mostly empty space?
In the gold foil scattering experiment by Rutherford and his team, almost all alpha particles passed straight through the foil. There were minor deflections mostly, and only a small amount of them showed deflections at really large angles. Only a few of them rebounded. This was the main observation that led Rutherford to conclude that the positive charge and mass of the atom concentrate at a very tiny section of the atom. That’s the nucleus. The other observation was that the entire atom must be space where the alpha particles could go undeflected.
What is the energy of the electron according to Rutherford’s model of the atom?
In Rutherford's model, electrostatic force provides the centripetal force:
∈
Kinetic Energy (K):
Potential Energy (U):
Total Energy (E):
Note that, E is the Epsilon symbol.
Physics Atoms Exam
Student Forum
Other Class 12th Physics Chapters
- Physics Alternating Current
- Physics Ray Optics and Optical Instruments
- Physics Electromagnetic Induction
- Physics Dual Nature of Radiation and Matter
- Physics Semiconductor Devices
- Physics Wave Optics
- Physics Current Electricity
- Physics Nuclei
- Physics Electrostatic Potential and Capacitance
- Physics Atoms
- Physics Moving Charges and Magnetism
- NCERT Class 12 Notes
- NCERT Class 12 Physics
- Physics Electric Charge and Field
- Physics Electromagnetic Waves
- Physics Magnetism and Matter