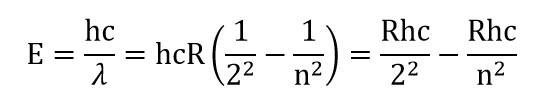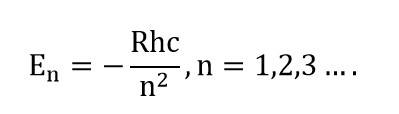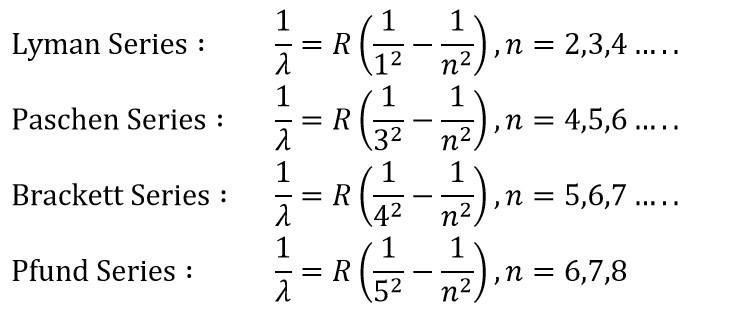In order to describe how electrons behave in an atom, Danish physicist Niels Bohr proposed Bohr's model of the atom in 1913. It was created as an advancement over Rutherford's atomic model, which was unable to account for the distinct lines observed in atomic spectra or the stability of atoms.
According to Bohr's concept, electrons travel in precise circular routes, known as orbits or energy levels, around the nucleus without losing energy. Electrons can move between the predetermined energy levels of each orbit by absorbing or releasing energy in the form of light. This model established the groundwork for contemporary atomic theory and effectively described the hydrogen line spectrum.
- Postulates Given By Bohr Model of Hydrogen Atom
- What is Bohr's Atomic Model?
- Hydrogen Like Atoms
- Definitions valid for single electron system
- Emission spectrum of hydrogen atom
- On Screen
- Wavelength of Photon Emitted in De-excitation
- Limitations of Bohr’s Model of Hydrogen Atom
Postulates Given By Bohr Model of Hydrogen Atom
The following are the postulates given by the Bohr Model of the Hydrogen Atom:
- Bohr said that electrons don’t just move anywhere—they follow certain fixed paths around the nucleus. These paths don’t change unless the electron gains or loses energy.
- Each path (or orbit) has a fixed amount of energy. If an electron stays in one path, its energy stays the same. That’s why atoms don’t collapse or give off energy all the time.
- When electrons jump from one orbit to another, they either take in energy or give it out. If they go to a higher level, they absorb energy. If they drop to a lower one, they release energy as light.
- Not all orbits are allowed. Only certain ones work, and that’s based on a rule about the electron’s motion—it has to fit in a way that depends on a number called Planck’s constant.
What is Bohr's Atomic Model?
In 1913, Prof. Niel Bohr removed the difficulties of Rutherford's atomic model by the application of Planck's quantum theory. For this he proposed the following postulates
(1) An electron moves only in certain circular orbits, called stationary orbits. In stationary orbits electron does not emit radiation, contrary to the predictions of classical electromagnetic theory.
(2) According to Bohr, there is a definite energy associated with each stable orbit and an atom radiaties energy only when it makes a transition from one of these orbits to another. If the energy of electron in the higher orbit be and that in the lower orbit be , then the frequency of the radiated waves is given by
(3) Bohr found that the magnitude of the electron's angular momentum is quantized, and this magnitude for the electron must be integral multiple of . The magnitude of the angular momentum is for a particle with mass moving with speed in a circle of radius . So, according to Bohr's postulate, )
Each value of corresponds to a permitted value of the orbit radius, which we will denote by The value of for each orbit is called principal quantum number for the orbit. Thus,
According to Newton's second law a radially inward centripetal force of magnitude
is needed by the electron which is being provided by the electrical attraction between the positive proton and the negative electron.
Thus,
Solving Eqs. (ii) and (iii), we get
The smallest orbit radius corresponds to . We'll denote this minimum radius, called the Bohr radius as ao. Thus,
Substituting values of and e , we get
Eq. (iv), in terms of ao can be written as,
Similarly, substituting values of and with in Eq. (v), we get
This is the greatest possible speed of the electron in the hydrogen atom. Which is approximately equal to
where
is the speed of light in vacuum.
Eq. (v), in terms of
can be written as,
Energy levels: Kinetic and potential energies and in th orbit are given by
(assuming infinity as a zero potential energy level)
The total energy
is the sum of the kinetic and potential energies.
so,
Substituting values of and with , we get the least energy of the atom in first orbit, which is -13.6 eV . Hence,
and
Substituting
, etc., we get energies of atom in different orbits.
Hydrogen Like Atoms
The Bohr model of hydrogen can be extended to hydrogen like atoms, i.e., one electron atoms, the nuclear charge is +ze, where is the atomic number, equal to the number of protons in the nucleus. The effect in the previous analysis is to replace every where by . Thus, the equations for, and are altered as under:
where (radius of first orbit of )
where (speed of electron in first orbit of )
where (energy of atom in first orbit of H )
Definitions valid for single electron system
(1) Ground state : Lowest energy state of any atom or ion is called ground state of the atom.
Ground state energy of H atom
Ground state energy of
Ion
Ground state energy of
Ion
(2) Excited State : State of atom other than the ground state are called its excited states.
| first excited state |
|
| second excited state |
|
| third excited state |
|
| excited state |
(3) Ionisation energy (I.E.) : Minimum energy required to move an electron from ground state to is called ionisation energy of the atom or ion
Ionisation energy of H atom
Ionisation energy of
Ion
Ionisation energy of
Ion
(4) Ionisation potential (I.P.) : Potential difference through which a free electron must be accelerated from rest such that its kinetic energy becomes equal to ionisation energy of the atom is called ionisation potential of the atom.
I. P of H atom
I.P. of
Ion
(5) Excitation energy : Energy required to move an electron from ground state of the atom to any other exited state of the atom is called excitation energy of that state.
Energy in ground state of H atom
Energy in first excited state of H -atom
excitation energy
.
(6) Excitation Potential : Potential difference through which an electron must be accelerated from rest so that its kinetic energy becomes equal to excitation energy of any state is called excitation potential of that state.
excitation energy
.
excitation potential
.
(7) Binding energy or Seperation energy : Energy required to move an electron from any state to
is called binding energy of that state. or energy released during formation of an H -like atom/ion from
to some particular n is called binding energy of that state.
Binding energy of ground state of H -atom
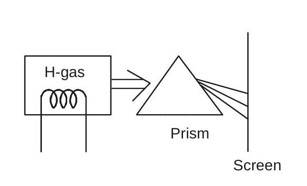
Emission spectrum of hydrogen atom
Under normal conditions the single electron in hydrogen atom stays in ground state ( ). It is excited to some higher energy state when it acquires some energy from external source. But it hardly stays there for more than second. A photon corresponding to a particular spectrum line is emitted when an atom makes a transition from a state in an excited level to a state in a lower excited level or the ground level.
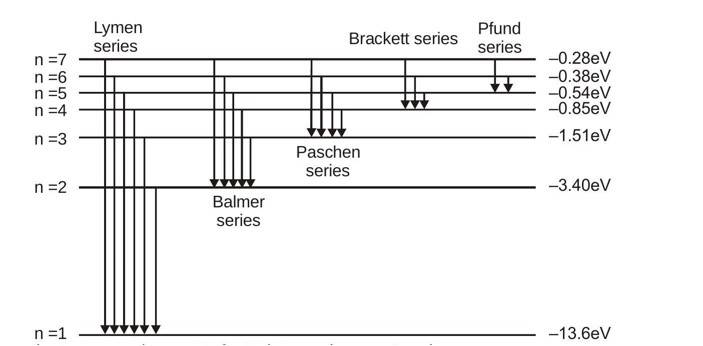
Let be the initial and the final energy state, then depending on the final energy state following series are observed in the emission spectrum of hydrogen atom.
On Screen
A photograph of spectral lines of the Lyman, Balmer, Paschen series of atomic hydrogen.
1, 2, 3.... represents the I, II & III line of Lyman, Balmer, Paschen series.
The hydrogen spectrum (some selected lines)
| Name of series |
Number of Line |
Quantum Number |
|||
| (Lower State |
(Upper State) |
Wavelength ( nm ) |
Energy |
||
| Lymen |
I |
1 |
2 |
121.6 |
10.2 eV |
| II |
1 |
3 |
102.6 |
12.09 eV |
|
| III |
1 |
4 |
97 |
12.78 eV |
|
| series limit |
1 |
∞ (series limit) |
91.2 |
13.6 eV |
|
| Balmer |
1 |
2 |
3 |
656.3 |
1.89 eV |
| II |
2 |
4 |
486.1 |
2.55 eV |
|
| III |
2 |
5 |
434.1 |
2.86 eV |
|
| series limit |
2 |
∞(series limit) |
364.6 |
3.41 eV |
|
| Paschen |
1 |
3 |
4 |
1875.1 |
0.66 eV |
| II |
3 |
5 |
1281.8 |
0.97 eV |
|
| III |
3 |
6 |
1093.8 |
1.13 eV |
|
| series limit |
3 |
∞ (series limit) |
822 |
1.51 eV |
|
Series limit : Line of any group having maximum energy of photon and minimum wavelength of that group is called series limit.
For the Lyman series , for Balmer series and so on.
Wavelength of Photon Emitted in De-excitation
According to Bohr when an atom makes a transition from higher energy level to a lower level it emits a photon with energy equal to the energy difference between the initial and final levels. If is the initial energy of the atom before such a transition, is its final energy after the transition, and the photon's energy is , then conservation of energy gives,
By 1913, the spectrum of hydrogen had been studied intensively. The visible line with longest wavelength, or lowest frequency is called
, the next line is called
and so on.
In 1885, Johann Balmer, a Swiss teacher found a formula that gives the wave lengths of these lines. This is now called the Balmer series. The Balmer's formula is,
Here,
, etc.
Rydberg constant
and
is the wavelength of light/photon emitted during transition,
For n = 3, we obtain the wavelength of
line.
Similarly, for n = 4, we obtain the wavelength of
line. For n = ∞, the smallest wavelength (=3646Å) of this series is obtained. Using the relation,E = hc/
we can find the photon energies corresponding to the wavelength of the Balmer series.
This formula suggests that,
The wavelengths corresponding to other spectral series (Lyman, Paschen, (etc.) can be represented by formula similar to Balmer's formula.
The Lyman series is in the ultraviolet, and the Paschen. Brackett and Pfund series are in the infrared region.
Limitations of Bohr’s Model of Hydrogen Atom
Physics Atoms Exam
Student Forum
Other Class 12th Physics Chapters
- Physics Alternating Current
- Physics Ray Optics and Optical Instruments
- Physics Electromagnetic Induction
- Physics Dual Nature of Radiation and Matter
- Physics Semiconductor Devices
- Physics Wave Optics
- Physics Current Electricity
- Physics Nuclei
- Physics Electrostatic Potential and Capacitance
- Physics Atoms
- Physics Moving Charges and Magnetism
- NCERT Class 12 Notes
- NCERT Class 12 Physics
- Physics Electric Charge and Field
- Physics Electromagnetic Waves
- Physics Magnetism and Matter