Think of a rope tied at a fixed end (A), and you're running in a circle holding the other end (B) of the rope. While running, two things are happening simultaneously: the position of the other end changes (B), and the rope creates an angle as you move around. This is one example; there are many similar examples, such as rotating fans, wheels, moving discs, etc..
All these examples deal with two types of velocities: linear velocity and angular velocity due to rotational motion around an axis. In class 11 Physics system of particles and rotation motion chapter covers this and related concepts. Students also need to understand Kinematics of Rotational Motion About a Fixed Axis to get the complete picture. We have discussed all the details related to linear and angular velocity, including differences, relations, applications, and more.
We have provided below short revision PDF for this topic on this page. Read the article below for complete information.
| Important Notes Link | |
|---|---|
| Class 11 Physics NCERT Notes | Class 12 NCERT Physics Notes |
- Definition of Angular Velocity
- Relation between Angular and Linear Velocity
- NCERT Insights of Angular Velocity
- Applications in Rotational Motion
- Important Point for Problem-Solving
- Solved Examples
- Practice Problems
Definition of Angular Velocity
Angular velocity is equivalent to linear velocity in linear motion. The linear velocity deals with change in the position of the object; likewise, angular velocity deals with change in angular position.
The rate of change of angular displacement of an object rotating about an axis is called angular velocity. If for a very small time interval dt the change in angular position is dθ , then the instantaneous angular velocity is defined as:
There are a few important things to notice:
- The SI unit of angular velocity is radians per second ( ).
- Angular velocity is a vector quantity.
- The direction determined by the right-hand rule: curl the fingers of your right hand in the direction of rotation, and the thumb points in the direction of .
- All points in a rotating rigid body have the same angular velocity, regardless of their distance from the axis.
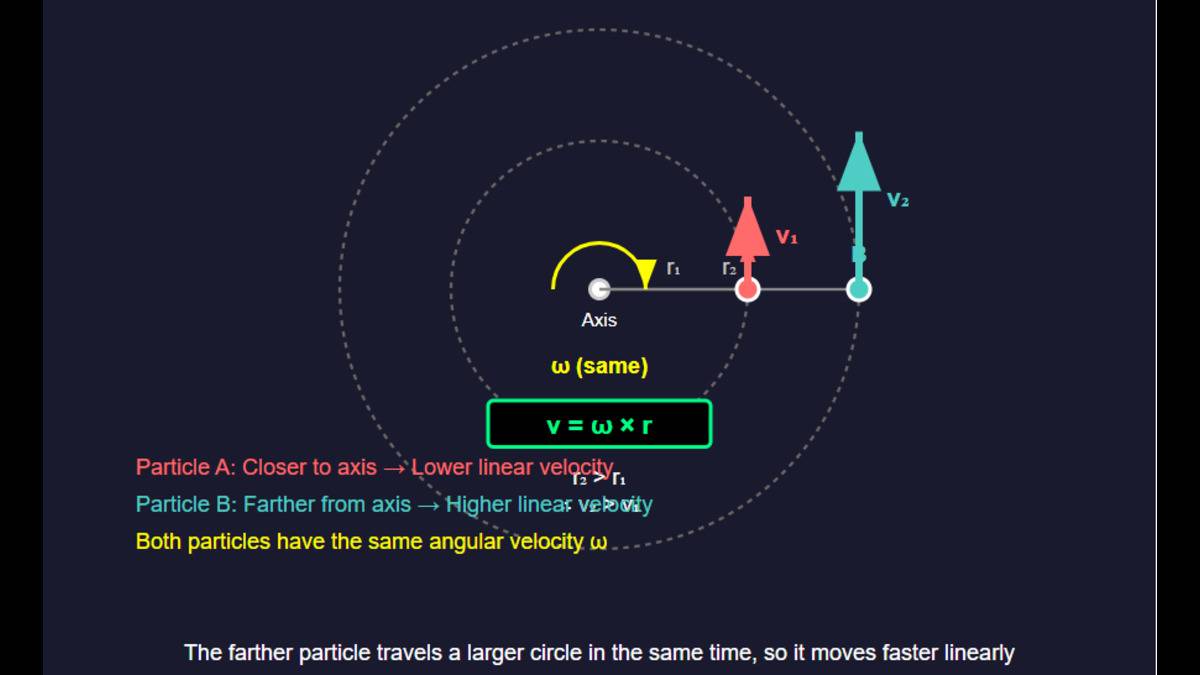
Relation between Angular and Linear Velocity
For a rotating rigid object, all its particles may have different linear velocities depending on the distance from the rotational axis. In simpler terms, you may understand it as you move further from the fixed axis, your distance increases, resulting in a higher linear velocity for the same angular velocity.
The linear velocity is equal to the cross product of the angular velocity and displacement vector (radius of the rotating circle). For a particle at a perpendicular distance from the axis of rotation, the linear velocity is given by:
Here,
- : position vector from the axis.
- : Linear velocity of the particle
- : Angular velocity of the rotating object.
- The cross product ensures that is perpendicular to both and .
- The magnitude of the linear velocity is:
Read More:
NCERT Insights of Angular Velocity
NCERT emphasises the purely rigid body in which, during rotational motion, each of the particles moves in a circular path with the same angular velocity. All particles moving with the same angular speed have different linear velocities due to their perpendicular distance from the rotational axis.
For example, in a rotating disc, a point farther from the center has a greater linear speed than one closer to the center. as you can check by using the formula , as you increase the value of r, v will simultaneously increase.
Applications in Rotational Motion
This relation is very vital in the rotation motion chapter. There are several applications of this chapter that you can check below:
- This relation is key to establishing several other important relations, such as the relation between angular and linear momentum and the relation between force and torque.
- Angular velocity is widely used in rotational dynamics.
- Its relation with linear velocity is very important for a good understanding of the rolling motion, which combines transitional and rotational motions.
- In pure rolling, the condition ensures that the point of contact with the surface is instantaneously at rest.
Read More:
Important Point for Problem-Solving
Many competitive exams, such as JEE and other, focuses on the relation of angular velocity and its conceptual usage in other relevant problems. Here are a few tips that can help you solve numerical of this topic.
- Identify the Axis of Rotation and it must be fixed to correctly apply .
- Use Vector Form to find the direction and magnitude of linear velocity.
- Always check no-slip condition holds true or not before appying the concepts of rolling motion.
- For 2D or 3D problems, always break down the velocities in components and then solve for each axis at a time or as the question requires.
- Always check units to ensure angular velocity is in rad/s and linear velocity in .
Solved Examples
Example 1: Linear Velocity of a Point on a Rotating Disc
A disc of radius 0.5 m rotates about its center with an angular velocity of . Find the linear velocity of a point on the rim.
Solution:
The direction is tangential to the rim, perpendicular to the radius vector.
Example 2: Rolling Without Slipping
A wheel of radius 0.2 m rolls without slipping on a horizontal surface with its center moving at . Calculate the angular velocity and the linear velocity of a point at the top of the wheel.
Solution:
For pure rolling, :
For the point at the top, the linear velocity is the sum of the center's velocity and the tangential velocity due to rotation:
Example 3: Vector Form Application
A particle rotates in a circle of radius 1 m about the z-axis with . If the particle's position is , find its linear velocity.
Solution:
The magnitude is , directed along the positive y -axis.
Practice Problems
1. A disc of radius 0.3 m rotates at . Find the linear speed of a point 0.1 m from the center.
2. A sphere rolls without slipping with a center-of-mass velocity of and radius 0.25 m . Calculate its angular velocity and the velocity of the point of contact with the ground.
3. A particle at rotates about the z -axis with Find its linear velocity vector.
Physics System of Particles and Rotational Motion Exam
Student Forum
Other Topics under this Chapter
- Overview
- Moment of Inertia
- Centre of Mass
- Motion of Centre of Mass
- Vector Product of Two Vectors
- Torque and Angular Momentum
- Equilibrium of a Rigid Body
- Linear Momentum of a System of Particles
- Angular Velocity and Relation with Linear Velocity
- Kinematics of Rotational Motion About a Fixed Axis
- Dynamics of Rotational Motion About a Fixed Axis
- Angular Momentum of Rotation About a Fixed Axis
- Streamline Flow
Other Class 11th Physics Chapters
- Physics Mechanical Properties of Solids
- NCERT Class 11 Physics
- NCERT Class 11 Notes
- NCERT Notes
- Physics Motion in Plane
- Physics Mechanical Properties of Fluids
- Physics Motion in Straight Line
- Physics System of Particles and Rotational Motion
- Physics Oscillations
- Physics Waves
- Physics Thermal Properties of Matter
- Physics Motion
- Physics Gravitation
- Physics Thermodynamics
- Physics Work, Energy and Power
- Physics Units and Measurement
- Physics Laws of Motion