Vector product of two vectors is a result of two vectors, which is perpendicular to both.
In Class 11 Physics, we have already encountered related concepts ranging from scalar multiplication to vector addition and subtraction, to understand multidimensional motion. After all this, we have to move forwards to solving problems in rotational dynamics, magnetic fields, and circular motion. These involve describing quantities that have direction, including torque and angular momentum.
Today, we will focus on the mathematical operation, cross product of two vectors. This is important for figuring out whether two vector quantities can create another vector, and if so, in which direction this new vector would go.
- Cross Product of Vectors Meaning
- Cross Product Formula: How We Determine It Mathematically
- Important Properties of Vector Product
- Real Life Applications of Cross Product of Two Vectors
- Geometric Interpretation of Cross Vector Product
- Cross Product of Vectors: Common Mistakes and Tips For Exams
- Practice Problem for Cross Vector of Products
- Use Physics Class 11 Notes for Quick Revisions
- Learn to Solve All NCERT Solutions Class 11 Physics
Cross Product of Vectors Meaning
The vector or cross product of two vectors and is denoted as . That results in a vector whose magnitude depends on the magnitudes of and . Besides the magnitude, the angle between them also matters. The direction is perpendicular to the plane formed by the two vectors. This mathematically proven operation captures the rotational effect of one vector acting relative to another.
If you are beginning to practice Class 11 NCERT Solutions for Chapter 6 Physics straightaway, remember these features of Vector Cross Product.
- What is the Vector Result? The cross product is a vector, not a scalar.
- Is it Perpendicular? The resulting vector is normal to the plane of and .
- What's the Magnitude Dependence? The magnitude involves the sine of the angle between the vectors.
Cross Product Formula: How We Determine It Mathematically
The vector product of vectors and is
You can see that and are the magnitudes of the vectors.
Following that, we have . That's the angle between and . - is a unit vector perpendicular to both and . It's pretty much determined by the right-hand rule, where you curl your fingers from to , while the thumb points along .
Based on all, the magnitude of the cross product is
This represents the area of the parallelogram formed by
and
.
Now, if we see in Cartesian coordinates, we can say that for
and
, the cross product is computed using the determinant
Important Properties of Vector Product
The cross product has some important properties that are applicable in solving problems faster.
- Cross product of a vector is non-commutative. Mathematically, that means . Simply put, reversing the order of the cross vector product flips the direction.
- The Result is zero for parallel vectors. If and are parallel ( or ), , so .
- Cross vector product follow orthogonality. What that means is that is perpendicular to both and .
- Cross vector product also has a distributive property. We can show that as .
Exam Tip on Cross Vector Product
Unit vector cross products are useful shortcuts.
Real Life Applications of Cross Product of Two Vectors
Everything you learn about rotational mechanics is dependent on the cross product of vectors.
- Torque is the Cause of Rotation: Torque about a point is defined as , where is the position vector from to the point of application of force The cross product of the vectors shows that torque is perpendicular to both and . That itself is behind driving rotation.
- Angular Momentum that Defines the Quantity of Motion: If you have learned about torque and angular momentum, you will be clear on the fact that angular momentum about a point is . The is linear momentum. This is essential when you are considering the conservation laws.
- Velocity in Rotational Motion: For a rigid body, the velocity of a point relative to is , where is angular velocity. This equation shows us, perfectly, how the rotational velocity vector ω creates a linear velocity v that is perpendicular to both the axis of rotation and the position vector r.
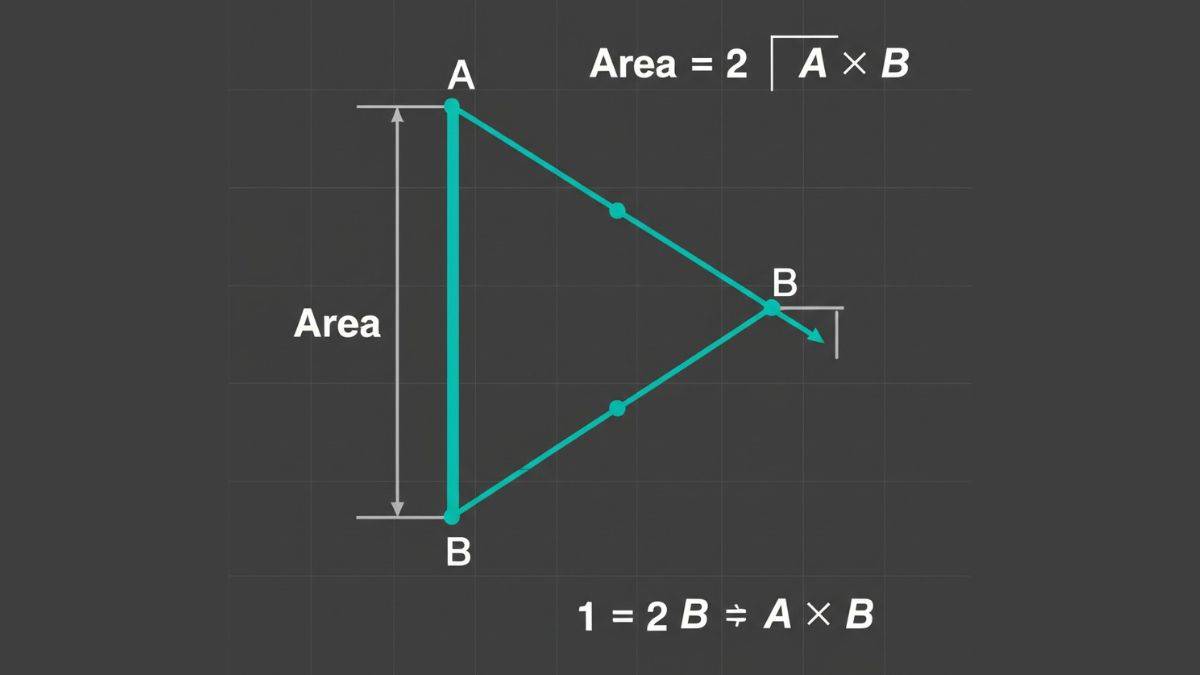
Geometric Interpretation of Cross Vector Product
The magnitude equals the area of the parallelogram formed by and . For a triangle formed by these vectors, the area is:
Geometrically, we can represent that as the image below.
Cross Product of Vectors: Common Mistakes and Tips For Exams
When preparing for exams or JEE main, be careful to avoid these common errors.
- Making Direction Errors. The quick fix for that would be to always use the right-hand rule to determine . Else, incorrect direction can lead to wrong signs.
- Wrongly Assuming Parallel Vectors. If , always check whether the vectors are parallel. It's important to check that before you begin to assume that it has zero magnitude.
Practice Problem for Cross Vector of Products
Here is an example problem on cross vector of product for you to work on.
Example: A force
acts at point
relative to the origin
. Find the torque about the origin.
Solution: Position vector .
Torque is:
Use Physics Class 11 Notes for Quick Revisions
Learn to Solve All NCERT Solutions Class 11 Physics
Commonly asked questions
What is the dot product of two vectors with itself?
The dot product of a vector with itself is the magnitude's square. When we multiply a vector by itself using the dot product, the angle between them is always zero. That's because the cosine of a 0° angle is 1. The dot product simplifies to the product of the magnitudes of the two vectors. And, in this case, it is the magnitude of the vector that is multiplied by itself. This operation results in a scalar quantity.
What is the product of two equal vectors?
The product of two equal vectors depends on what type of multiplication we are using.
Dot Product: The dot product of two equal vectors is the square of the magnitude of the vector. This is because the angle between two equal vectors is 0°, and the cosine of 0° is 1.
Cross Product: The vector product or cross product of two equal vectors is a zero vector (or null vector). This is because the angle between the vectors is zero, and the sine of 0° is 0.
What is the concept of the vector product of vectors Class 11?
The vector product is also known as the cross product of two vectors. This results in a new vector. For all Class 11 students in Physics, one key concept of the cross product is that this resultant vector is perpendicular to the plane containing the original two vectors. The magnitude of this new vector is calculated by multiplying the magnitudes of the two initial vectors and the sine of the angle between them. The direction of the resulting vector is determined by the right-hand rule.
Physics System of Particles and Rotational Motion Exam
Student Forum
Other Topics under this Chapter
- Overview
- Moment of Inertia
- Centre of Mass
- Motion of Centre of Mass
- Vector Product of Two Vectors
- Torque and Angular Momentum
- Equilibrium of a Rigid Body
- Linear Momentum of a System of Particles
- Angular Velocity and Relation with Linear Velocity
- Kinematics of Rotational Motion About a Fixed Axis
- Dynamics of Rotational Motion About a Fixed Axis
- Angular Momentum of Rotation About a Fixed Axis
- Streamline Flow
Other Class 11th Physics Chapters
- Physics Mechanical Properties of Solids
- NCERT Class 11 Physics
- NCERT Class 11 Notes
- NCERT Notes
- Physics Motion in Plane
- Physics Mechanical Properties of Fluids
- Physics Motion in Straight Line
- Physics System of Particles and Rotational Motion
- Physics Oscillations
- Physics Waves
- Physics Thermal Properties of Matter
- Physics Motion
- Physics Gravitation
- Physics Thermodynamics
- Physics Work, Energy and Power
- Physics Units and Measurement
- Physics Laws of Motion