Moment of Inertia: Class 11 Physics Notes, Definition, Working Principle, Formula & Real-Life Applications

MOMENT OF INERTIA

Like the centre of mass, the moment of inertia is a property of an object that is related to its mass distribution. The moment of inertia (denoted by I) is an important quantity in the study of system of particles that are rotating. The role of the moment of inertia in the study of rotational motion is analogous to that of mass in the study of linear motion.

Moment of inertia gives a measurement of the resistance of a body to a change in its rotational motion. If a body is at rest, the larger the moment of inertia of a body the more difficuilt it is to put that body into rotational motion. Similarly, the larger the moment of inertia of a body, the more difficult to stop its rotational motion. The moment of inertia is calculated about some axis (usually the rotational axis).

Moment of inertia depends on :

(i) Density of the material of body

(ii) Shape & size of body

(iii) Axis of rotation

In totality we can say that it depends upon distribution of mass relative to axis of rotation.

Note:

Moment of inertia does not change if the mass:
(i) is shifted parallel to the axis of the rotation

(ii) is rotated with constant radius about axis of rotation

1. Moment of Inertia of a Single Particle

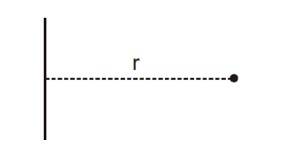
For a very simple case the moment of inertia of a single particle about an axis is given by, I = mr²   ..........(i)

Here, m is the mass of the particle and r its distance from the axis under consideration.

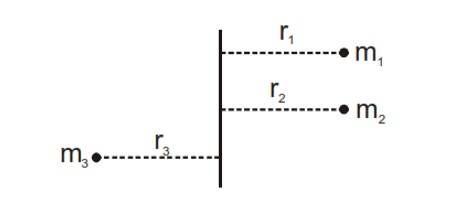
2. Moment of Inertia of a System of Particles

The moment of inertia of a system of particles about an axis is given by, $\begin{array}{c}I=\underset{i}{\sum } m_i{r}_i^2\#\left(ii\right)\end{array}$

where $r_i$  is the perpendicular distance from the axis to the $i$ th particle, which has a mass $m_i$ .

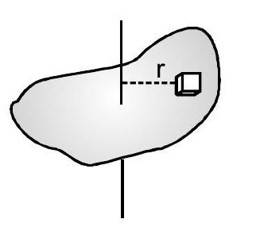
3. Moment of Inertia of Rigid Bodies

For a continuous mass distribution such as found in a rigid body, we replace the summation of $I=\underset{i}{\sum } m_i{r}_i^2$ by an integral. If the system is divided into infinitesimal element of mass $dm$ and if $r$ is the distance from a mass element to the axis of rotation, the moment of inertia is, $\mathrm{I}=\int {\mathrm{r}}^2\mathrm{d}\mathrm{m}$ where the integral is taken over the system.

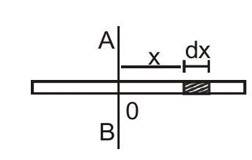
(A) Uniform rod about a perpendicular bisector

Consider a uniform rod of mass $M$ and length $l$ figure and suppose the moment of inertia is to be calculated about the bisector AB. Take the origin at the middle point $O$ of the rod. Consider the element of the rod between a distance $x$ and $x+dx$ from the origin. As the rod is uniform, Mass per unit length of the rod $=M/l$ so that the mass of the element $=(M/l)\mathrm{d}\mathrm{x}$ . The perpendicular distance of the element from the line $AB$ is $x$ . The moment of inertia of this element about is $\mathrm{d}\mathrm{I}=\frac{\mathrm{M}}{l}\mathrm{d}\mathrm{x}{\mathrm{x}}^2.$

When $x=-l/2$ , the element is at the left end of the rod. As $x$ is changed from $-l/2$ to $l/2$ , the elements cover the whole rod.
Thus, the moment of inertia of the entire rod about $AB$ is $\mathrm{I}={\int }_{-l/2}^{l/2} \frac{\mathrm{M}}{l}{\mathrm{x}}^2\mathrm{d}\mathrm{x}={\left[\frac{\mathrm{M}{\mathrm{x}}^3}{l3}\right]}_{-l/2}^{l/2}=\frac{{\mathrm{M}}^2}{12}$

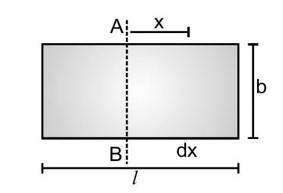
(B) Moment of inertia of a rectangular plate about a line parallel to an edge and passing through the centre

The situation is shown in figure. Draw a line parallel to $AB$ at a distance $x$ from it and another at a distance $x+dx$ . We can take the strip enclosed between the two lines as the small element.

It is "small" because the perpendiculars from different points of the strip to AB differ by not more than dx . As the plate is uniform, its mass per unit area $=\frac{\mathrm{M}}{\mathrm{b}l}$
Mass of the strip $=\frac{M}{bl}\mathrm{b}\mathrm{d}\mathrm{x}=\frac{\mathrm{M}}{l}\mathrm{d}\mathrm{x}$ .

The perpendicular distance of the strip from $AB=x$ .
The moment of inertia of the strip about $AB=dI=\frac{M}{l}dx{x}^2$ . The moment of inertia of the given plate is, therefore, $\mathrm{I}={\int }_{-l/2}^{l/2} \frac{\mathrm{M}}{l}{\mathrm{x}}^2\mathrm{d}\mathrm{x}=\frac{\mathrm{M}{l}^2}{12}$

The moment of inertia of the plate about the line parallel to the other edge and passing through the centre may be obtained from the above formula by replacing $l$ by b and thus, $\mathrm{I}=\frac{{\mathrm{M}\mathrm{b}}^2}{12}$

(C) Moment of inertia of a circular ring about its axis (the line perpendicular to the plane of the ring through its centre)

Suppose the radius of the ring is R and its mass is M . As all the elements of the ring are at the same perpendicular distance $R$ from the axis, the moment of inertia of the ring is $\mathrm{I}=\int {\mathrm{r}}^2\mathrm{d}\mathrm{m}=\int {\mathrm{R}}^2\mathrm{d}\mathrm{m}={\mathrm{R}}^2\int \mathrm{d}\mathrm{m}={\mathrm{M}\mathrm{R}}^2.$

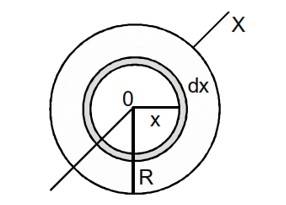
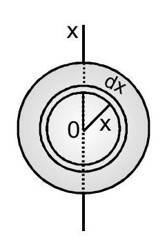
(D) Moment of inertia of a uniform circular plate about its axis

Let the mass of the plate be $M$ and its radius $R$ . The centre is at $O$ and the axis $OX$ is perpendicular to the plane of the plate.

Draw two concentric circles of radii $x$ and $x+dx$ , both centred at $O$ and consider the area of the plate in between the two circles.
This part of the plate may be considered to be a circular ring of radius $x$ . As the periphery of the ring is $2\pi x$ and its width is $dx$ , the area of this elementary ring is $2\pi xdx$ . The area of the plate is $\pi {\mathrm{R}}^2$ . As the plate is uniform,
Its mass per unit area $=\frac{M}{\pi R^2}$
Mass of the ring $=\frac{M}{\pi R^2}2\pi xdx=\frac{2Mxdx}{R^2}$
Using the result obtained above for a circular ring, the moment of inertia of the elementary ring about OX is $\mathrm{d}\mathrm{I}=\left[\frac{2\mathrm{M}\mathrm{x}\mathrm{d}\mathrm{x}}{{\mathrm{R}}^2}\right]{\mathrm{x}}^2.$

The moment of inertia of the plate about OX is $\mathrm{I}={\int }_0^{\mathrm{R}} \frac{2\mathrm{M}}{{\mathrm{R}}^2}{\mathrm{x}}^3\mathrm{d}\mathrm{x}=\frac{{\mathrm{M}\mathrm{R}}^2}{2}.$

(E) Moment of inertia of a hollow cylinder about its axis

Suppose the radius of the cylinder is $R$ and its mass is $M$ . As every element of this cylinder is at the same perpendicular distance $R$ from the axis, the moment of inertia of the hollow cylinder about its axis is $\mathrm{I}=\int {\mathrm{r}}^2\mathrm{d}\mathrm{m}={\mathrm{R}}^2\int \mathrm{d}\mathrm{m}={\mathrm{M}\mathrm{R}}^2$

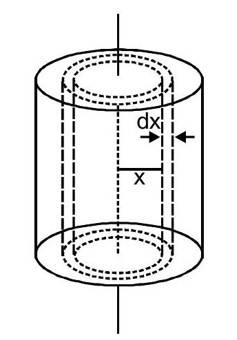
(F) Moment of inertia of a uniform solid cylinder about its axis

Let the mass of the cylinder be $M$ and its radius $R$ . Draw two cylindrical surface of radii $x$ and $x+dx$ coaxial with the given cylinder. Consider the part of the cylinder in between the two surface. This part of the cylinder may be considered to be a hollow cylinder of radius $x$ . The area of cross-section of the wall of this hollow cylinder is $2\pi \times \mathrm{d}\mathrm{x}$ . If the length of the cylinder is $l$ , the volume of the material of this elementary hollow cylinder is $2\pi \times \mathrm{d}\mathrm{x}\mathrm{l}$ .
The volume of the solid cylinder is $\pi {\mathrm{R}}^{2}l$ and it is uniform, hence its mass per unit volume is $\rho =\frac{\mathrm{M}}{\pi {\mathrm{R}}^{2}l}$

The mass of the hollow cylinder considered is $\frac{\mathrm{M}}{\pi {\mathrm{R}}^{2}l}2\pi \mathrm{x}\mathrm{d}\mathrm{x}l=\frac{2\mathrm{M}}{{\mathrm{R}}^2}\mathrm{x}\mathrm{d}\mathrm{x}.$

As its radius is $x$ , its moment of inertia about the given axis is $\mathrm{d}\mathrm{I}=\left[\frac{2\mathrm{M}}{{\mathrm{R}}^2}\mathrm{x}\mathrm{d}\mathrm{x}\right]{\mathrm{x}}^2.$

The moment of inertia of the solid cylinder is, therefore, $I={\int }_0^R \frac{2M}{R^2}{x}^{3}dx=\frac{M{R}^2}{2}.$

Note that the formula does not depend on the length of the cylinder.

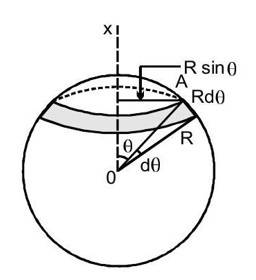
(G) Moment of inertia of a uniform hollow sphere about a diameter

Let M and R be the mass and the radius of the sphere, O its centre and OX the given axis (figure). The mass is spread over the surface of the sphere and the inside is hollow.
Let us consider a radius OA of the sphere at an angle $\theta$ with the axis OX and rotate this radius about OX. The point A traces a circle on the sphere. Now change $\theta$ to $\theta +d\theta$ and get another circle of somewhat larger radius on the sphere. The part of the sphere between these two circles, shown in the figure, forms a ring of radius $\mathrm{R}\mathrm{s}\mathrm{i}\mathrm{n}\theta$ . The width of this ring is $\mathrm{R}\mathrm{d}\theta$ and its periphery is $2\pi R\mathrm{s}\mathrm{i}\mathrm{n}\theta$ . Hence, the area of the ring $=(2\pi R\mathrm{s}\mathrm{i}\mathrm{n}\theta )\left(Rd\theta \right)$ .

Mass per unit area of the sphere $=\frac{M}{4\pi R^2}$ .
The mass of the ring $=\frac{M}{4\pi R^2}(2\pi R\mathrm{s}\mathrm{i}\mathrm{n}\theta )\left(Rd\theta \right)=\frac{M}{2}\mathrm{s}\mathrm{i}\mathrm{n}\theta d\theta$ .
The moment of inertia of this elemental ring about OX is

As $\theta$ increases from 0 to $\pi$ , the elemental rings cover the whole spherical surface. The moment of inertia of the hollow sphere is, therefore, $I={\int }_0^{\pi } \frac{M}{2}{R}^2{\mathrm{s}\mathrm{i}\mathrm{n}}^3\theta d\theta =\frac{M{R}^2}{2}\left[{\int }_0^{\pi } \left(1-{\mathrm{c}\mathrm{o}\mathrm{s}}^2\theta \right)\mathrm{s}\mathrm{i}\mathrm{n}\theta d\theta \right]=\frac{M{R}^2}{2}\left[{\int }_{\theta =0}^{\pi } -\left(1-{\mathrm{c}\mathrm{o}\mathrm{s}}^2\theta \right)d(\mathrm{c}\mathrm{o}\mathrm{s}\theta )\right]$

$=\frac{-{\mathrm{M}\mathrm{R}}^2}{2}{\left[\mathrm{c}\mathrm{o}\mathrm{s}\theta -\frac{{\mathrm{c}\mathrm{o}\mathrm{s}}^3\theta }{3}\right]}_0^{\pi }=\frac{2}{3}{\mathrm{M}\mathrm{R}}^2$

(H) Moment of inertia of a uniform solid sphere about a diameter

Let M and R be the mass and radius of the given solid sphere. Let O be centre and OX the given axis. Draw two spheres of radii $x$ and $x+dx$ concentric with the given solid sphere. The thin spherical shell trapped between these spheres may be treated as a hollow sphere of radius $x$ .
The mass per unit volume of the solid sphere $=\frac{\mathrm{M}}{\frac{4}{3}\pi {\mathrm{R}}^3}=\frac{3\mathrm{M}}{4\pi {\mathrm{R}}^3}$

 

The thin hollow sphere considered above has a surface area $4\pi x^2$ and thickness $dx$ . Its volume i $4\pi x^{2}dx$ and hence its mass is $=\left(\frac{3M}{4\pi R^3}\right)\left(4\pi x^{2}dx\right)=\frac{3M}{R^3}{x}^{2}dx$

Its moment of inertia about the diameter OX is, therefore, $\mathrm{d}\mathrm{l}=\frac{2}{3}\left[\frac{3\mathrm{M}}{{\mathrm{R}}^3}{\mathrm{x}}^2\mathrm{d}\mathrm{x}\right]{\mathrm{x}}^2\mathrm{}=\frac{2\mathrm{M}}{{\mathrm{R}}^3}{\mathrm{x}}^4\mathrm{d}\mathrm{x}$

If $x=0$ , the shell is formed at the centre of the solid sphere. As $x$ increases from 0 to $R$ , the shells cover the whole solid sphere.
The moment of inertia of the solid sphere about OX is, therefore, $I={\int }_0^R \frac{2M}{R^3}{x}^{4}dx=\frac{2}{5}M{R}^2$

4. Moment of Inertia of Compound Bodies

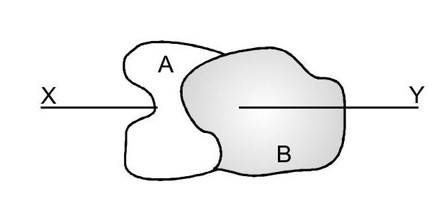
Consider two bodies A and B, rigidly joined together. The moment of inertia of this compound body, about an axis XY, is required. If $I_A$ is the moment of inertia of body A about XY. $I_B$ is the moment of inertia of body B about XY. Then, moment of Inertia of compound body I = I_A +I_B Extending this argument to cover any number of bodies rigidly joined together, we see that the moment of inertia of the compound body, about a specified axis, is the sum of the moments of inertia of the separate parts of the body about the same axis.

There are two important theorems on moment of inertia, which, in some cases enable the moment of inertia of a body to be determined about an axis, if its moment of inertia about some other axis is known. Let us now discuss both of them.

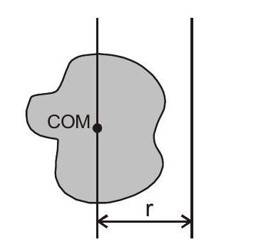
Theorem of parallel axes

A very useful theorem, called the parallel axes theorem relates the moment of inertia of a rigid body about two parallel axes, one of which passes
through the centre of mass.
Two such axes are shown in figure for a body of mass M. If r is the distance between the axes and ${\mathrm{I}}_{\text{сом }}$ and I are the respective

 moments of inertia about them, these moments are related by, $\mathrm{I}={\mathrm{I}}_{\mathrm{c}\mathrm{o}\mathrm{m}}+{\mathrm{M}\mathrm{r}}^2$

• Theorem of parallel axis is applicable for any type of rigid body whether it is a two dimensional or three dimensional

Theorem of perpendicular axes

The theorem states that the moment of inertia of a plane lamina about an axis perpendicular to the plane of the lamina is equal to the sum of the moments of inertia of the lamina about two axes perpendicular to each other, in its own plane and intersecting each other, at the point where the perpendicular axis passes through it.
Let x and y axes be chosen in the plane of the body and z-axis perpendicular, to this plane, three axes being mutually perpendicular, then the theorem states that.

Important point in perpendicular axis theorem

(i) This theorem is applicable only for the plane bodies (two dimensional).

(ii) In theorem of perpendicular axes, all the three axes (x,y and z ) intersect each other and this point may be any point on the plane of the body (it may even lie outside the body).

(iii) Intersection point may or may not be the centre of mass of the body.

Radius of gyration is a way to figure out how far the mass of something "acts" from the center when it spins. Imagine you could take all the weight in a spinning object and move it so it’s all at the same distance from the axis—and it would still spin the same way. That distance? That’s what we call the radius of gyration. For example, think about a spinning wheel. If the weight is mostly near the edge, it feels harder to spin—that means a bigger radius of gyration. If everything’s packed close to the center, it’s easier to turn, and the radius is smaller.

$K=\sqrt{\frac{I}{m}}$

where:

K is the radius of gyration

I is moment of inertia

and m is mass.