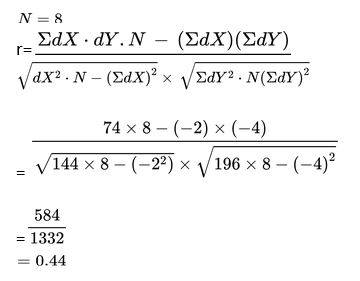Correlation and Regression: Notes, Definition, Formula, Solved Examples & FAQs

Updated on Jun 10, 2025 15:03 IST

Correlation and Regression are important topics in statistics. They are used to study the relationship between two or more variables. While both are used to understand relationships between variables, they are distinct statistical methods.

Correlation is used to study the strength and direction of two variables, while regression analyzes how a variable (dependent variable) is affected due to another variable (independent). This topic is important for board examiners. Students can go through the article and know more about correlation and regression in detail.

Also Read: NCERT Solution for Class 11 & 12

Table of content

What is Correlation?
What is Regression?
Difference Between Correlation and Regression
Weightage of Correlation and Regression
Illustrative examples on Correlation and Regression
FAQs on Correlation and Regression

What is Correlation?

Correlation, a statistical concept, is used to calculate the value of the relationship between variables. A real-life example of what this technique calculates is the relationship between price and demand.

Types of Correlation

Correlation can be classified into the following categories.

Positive and Negative Correlation
Linear and Non-Linear Correlation
Simple, Multiple and Partial Correlation

Techniques for measuring correlation

The various techniques used to measure correlation are :

Scatter diagram
Karl Pearson’s Coefficient of Correlation is represented by the formula

What is Regression?

Regression is a concept in statistics that is used to predict outcomes, understand relationships, and make data-driven decisions. Common types of regression include simple linear regression, multiple linear regression, logistic regression, and non-linear regression. The main uses of regression are prediction, trend analysis, and building relationships.

Difference Between Correlation and Regression

Below are the key differences between correlation and regression.

Features	Correlation	Regression
Use	Analyze relationship	Prediction and estimation
Primary goal	Measure strength and direction	Predict the value of a variable
Direction	Symmetrical	One-way
Output	Correlation coefficient (r)	Regression equation (Y = a + bX)

Weightage of Correlation and Regression

The concept of correlation and regression is introduced to the students of grade 11 as a part of statistics. The following concept generates high amounts of knowledge, especially in the field of data science. Regression is not evaluated while correlation is tested for 4-8 marks.

Illustrative examples on Correlation and Regression

1. Calculate the correlation coefficient between the heights of fathers in inches (X) and their sons (Y)

X	65	66	57	67	68	69	70	72
Y	67	56	65	68	72	72	69	71

Solution.

X	dx(d from AM=67)	dX²	Y	dY(d from AM=68)	dY²	dXdY
65	-2	4	67	-1	1	2
66	-1	1	56	-12	144	12
57	-10	100	65	-3	9	30
67	0	0	68	0	0	0
68	+1	1	72	4	16	4
69	+2	4	72	4	16	8
70	+3	9	69	1	1	3
72	5	25	71	3	9	15
ΣX = 534	ΣdX = -2	ΣdX² = 144	ΣY = 540	ΣdY = -4	ΣrdY² = 196	ΣdXdY=74

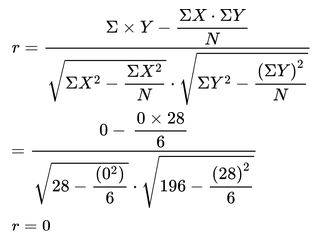
2. Calculate the correlation coefficient between X and Y and comment on their relationship.

X	-3	-2	-1	1	2	3
Y	9	4	1	1	4	9

Solution.

X	Y	X²	Y²	XY
-3	9	9	81	-27
-2	4	4	16	-8
-1	1	1	1	-1
1	1	1	1	1
2	4	4	16	8
3	9	9	81	27

There is no linear correlation between the two variables, as X and Y are uncorrected.

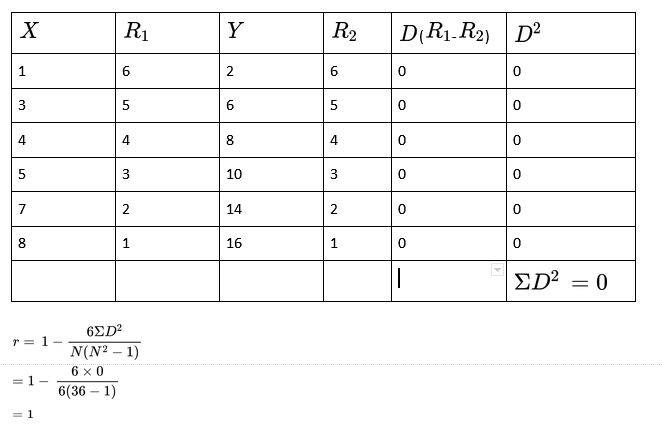
3. Calculate the correlation coefficient between X and Y and comment on their relationship

X	1	3	4	5	7	8
Y	2	6	8	10	14	16

Solution.

∴The two variables are perfectly positive correlated.

FAQs on Correlation and Regression

Q: When two variables move in the same direction, what is the nature of the correlation of two variables?

A: The value of the correlation would be positive in nature.

Q: What is the arithmetical representation of the Coefficient of correlation existing between -1 and +1?

A: The correlation is perfectly negative when the value of the coefficient of correlation is -1, and the correlation is perfectly positive when the value of the coefficient of correlation is +1.

Q: When is the method of rank correlation used for calculation?

A: When variables are qualitative such as wisdom, beauty, bravery and so on are used.

Q: Define Regression

A: Linear regression can be defined as a statistical model used to represent the relationship between a scalar variable and an independent/dependent variable.

Q: Define the line of best fit.

A: The line of the best fit is the line that passes through the scattered points such that it covers up or represents most of these points. Approximately half of the points that are scattered should be on either side of this line.