For a perfect gas, two pressures P1 and P2 are shown in figure. The graph shows:

Insufficient data to drawn any conclusion

What are Inverse Trigonometric Functions: Formula, Graphs and Properties

Updated on Jun 20, 2025 13:31 IST

By Jaya Sharma, Assistant Manager - Content

Inverse trigonometric functions, also known as inverse trig functions or arcus functions, are the inverses of the standard trigonometric functions (sine, cosine, tangent, etc.). They are used to find the angle when the value of the trigonometric function is known. Inverse trigonometric functions define integrals making them important for calculus as well with various applications in science and engineering. Even entrance examinations such as JEE Main and IIT JAM ask questions based on the conceptual applications of these topics. The following table gives inverse trigonometric functions along with their range and domain:

Function	Domain	Range
$\sin^{-1}$	$[−1, 1]$	$[- \frac{π}{2}, \frac{π}{2}]$
$\cos^{-1}$	$[−1, 1]$	$[0, π]$
$\csc^{-1}$	$R ∖ (−1, 1)$	$[- \frac{π}{2}, \frac{π}{2}] ∖ {0}$
$\sec^{-1}$	$R ∖ (−1, 1)$	$[0, π] ∖ {\frac{π}{2}}$
$\tan^{-1}$	$R$	$(- \frac{π}{2}, \frac{π}{2})$
$\cot^{-1}$	$R$	$(0, π)$

Table of content

Inverse Trigonometric Functions Formula
What is Arc sine function or Inverse sine function?
What is Arc cosine function or Inverse cosine function?
Understanding Arc tangent function or Inverse Tangent Function
Arc co-tangent function or Inverse co-tangent function
What is Arc secant function or Inverse secant function?
Understanding Arc cosecant function or Inverse cosecant function
Derivatives of Inverse Trigonometric Functions
What are the Properties of Inverse Trigonometric Functions?
Important Points Related to Inverse Trigonometric Functions

Inverse Trigonometric Functions Formula

The following table provides the inverse triginometric functions formula for users to learn. These are essential for entrance exams like NEET and CUET since they are used in different questions asked.

Inverse Trigonometric Function	Formula
Arccosine	$\cos^{-1} (- x) = π - \cos^{-1} (x), x \in [- 1, 1]$
Arctangent	$\tan^{-1} (- x) = - \tan^{-1} (x), x \in ℝ$
Arcsine	$\sin^{-1} (- x) = - \sin^{-1} (x), x \in [- 1, 1]$
Arcsecant	$\sec^{-1} (- x) = π - \sec^{-1} (x), \| x \| \geq 1$
Arccotangent	$\cot^{-1} (- x) = π - \cot^{-1} (x), x \in ℝ$
Arccosecant	$\csc^{-1} (- x) = - \csc^{-1} (x), \| x \| \geq 1$

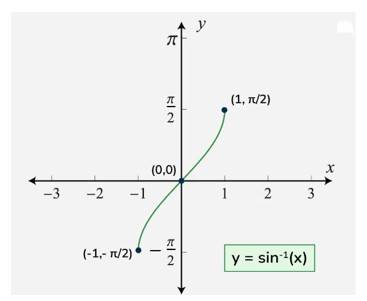
What is Arc sine function or Inverse sine function?

(a) The inverse sine function, also known as arcsine, is the inverse of the sine function. It is denoted as sin⁻¹ or arcsin. The inverse sine function takes a ratio of the opposite side to the hypotenuse in a right-angled triangle and returns the corresponding angle.

(b) Inverse sine function is written as $s i n^{- 1} x$ .

(d) Range of $s i n^{- 1} x$ is $[- \frac{π}{2}, \frac{π}{2}]$ .

(e) The inverse sine function "undoes" the sine function, meaning sin(arcsin(x)) = x for all x in the domain of arcsin.

(f) The graph of $s i n^{- 1} x$ is shown in fig.

Some relevant reads:

NCERT solutions	NCERT Class 11 Math Notes
NCERT Class 12 Maths Notes for CBSE	CBSE Class 12 NCERT Notes

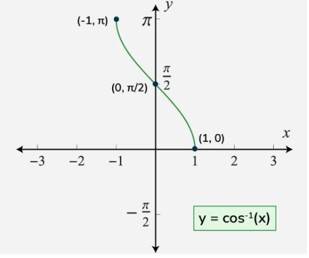
What is Arc cosine function or Inverse cosine function?

(a) The inverse cosine function, also known as arccosine, is denoted as cos⁻¹(x) or arccos(x). It's the inverse of the standard cosine function and is used to find the angle (in radians or degrees) whose cosine is equal to a given value. Essentially, if cos(θ) = x, then θ = cos⁻¹(x).

(b) Inverse cosine function is written as $c o s^{- 1} x$ .

(d) Range of $c o s^{- 1} x$ is $[0, π]$ .

(e) The inverse of a function "undoes" the original function. If f(a) = b, then f⁻¹(b) = a.

(f) The graph of $c o s^{- 1} x$ is shown in fig.

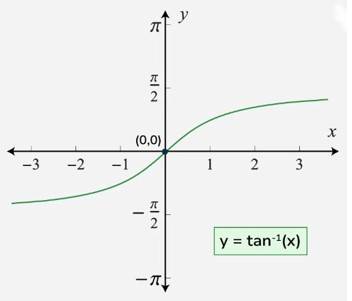
Understanding Arc tangent function or Inverse Tangent Function

(a) The tan inverse function, also known as arctan or tan⁻¹(x), is the inverse of the tangent function. It takes a ratio of the opposite side to the adjacent side in a right triangle and returns the angle in radians or degrees. The inverse tangent function is denoted by tan⁻¹x or arctan(x). This is an important function for those who are planning to take IISER exam.

(b) Inverse tangent function is written as $t a n^{- 1} x$ .

(d) Range of $t a n^{- 1} x$ is $(- \frac{π}{2}, \frac{π}{2})$ .

(e) The tan inverse function reverses the relationship of the tangent function. If tan(θ) = x, then θ = tan⁻¹(x).

(f) The graph of $t a n^{- 1} x$ is shown in fig.

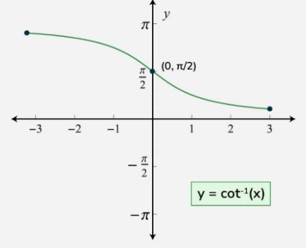
Arc co-tangent function or Inverse co-tangent function

(a) The inverse cotangent function, also known as arccotangent or arccot, is the inverse of the cotangent function. It is denoted as arccot(x) or cot⁻¹(x). The arccot function takes a real number 'x' as input and returns the angle whose cotangent is equal to 'x'.

(b) Inverse co-tangent function is written as $c o t^{- 1} x$ .

(d) Range of $c o t^{- 1} x$ is $(0, π)$ .

(e) The inverse of a function "undoes" the operation of the original function. So, if cot(θ) = x, then arccot(x) = θ.

(f) The graph of $c o t^{- 1} x$ is shown in fig.

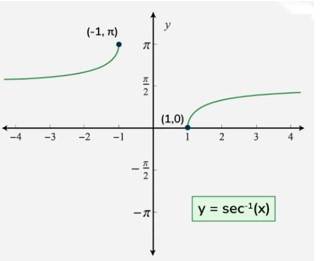
What is Arc secant function or Inverse secant function?

(a) It is the inverse of the secant function. It returns the angle whose secant is equal to x.

(b) Inverse secant function is written as $s e c^{- 1} x$ .

(d) Range of $s e c^{- 1} x$ is $[0, π] - {\frac{π}{2}}$ or $[0, \frac{π}{2}) \cup (\frac{π}{2}, π]$ .

(e) The graph of $s e c^{- 1} x$ is shown in fig.

Understanding Arc cosecant function or Inverse cosecant function

(a) The arccosecant function takes a cosecant value (which is a ratio of the hypotenuse to the opposite side in a right triangle) and returns the angle whose cosecant is that value.

(b) The inverse of the cosecant function, often denoted as cosec⁻¹(x) or arccsc(x), is the arccosecant function. It is also known as the inverse cosecant.

(d) Domain of $c o s e c^{- 1} x$ is R $- (- 1, 1)$ .

(e) Range of $c o s e c^{- 1} x$ is $[- \frac{π}{2}, \frac{π}{2}]$ $- {0}$ or $[- \frac{π}{2}, 0) \cup (0, \frac{π}{2}]$ .

(f) The graph of $c o s e c^{- 1} x$ is shown in fig.

Derivatives of Inverse Trigonometric Functions

Derivatives of all inverse trigonometric functions is first-order derivatives.

Inverse Trig Function	`dy/dx`
$y = \tan^{-1} (x)$	$\frac{1}{(1 + x^{2})}$
$y = \cot^{-1} (x)$	$- \frac{1}{(1 + x^{2})}$
$y = \sin^{-1} (x)$	$\frac{1}{\sqrt{1 - x^{2}}}$
$y = \cos^{-1} (x)$	$- \frac{1}{\sqrt{1 - x^{2}}}$
$y = \sec^{-1} (x)$	$\frac{1}{\| x \| \sqrt{x^{2} - 1}}$
$y = \csc^{-1} (x)$	$- \frac{1}{\| x \| \sqrt{x^{2} - 1}}$

What are the Properties of Inverse Trigonometric Functions?

The following properties are important for solving equations involving inverse trigonometric functions and for calculus applications:

1. Domain and Range

Arcsine (sin⁻¹ x or arcsin x)

Domain: [-1, 1]

Range: [-π/2, π/2]

Arccosine (cos⁻¹ x or arccos x)

Domain: [-1, 1]

Range: [0, π]

Arctangent (tan⁻¹ x or arctan x)

Domain: (-∞, ∞)

Range: (-π/2, π/2)

Arccotangent (cot⁻¹ x or arccot x)

Domain: (-∞, ∞)

Range: (0, π)

Arcsecant (sec⁻¹ x or arcsec x)

Domain: (-∞, -1] ∪ [1, ∞)

Range: [0, π/2) ∪ (π/2, π]

Arccosecant (csc⁻¹ x or arccsc x)

Domain: (-∞, -1] ∪ [1, ∞)

Range: [-π/2, 0) ∪ (0, π/2]

2. Fundamental Identities

Basic inverse relationships

sin(sin⁻¹ x) = x for x ∈ [-1, 1]

cos(cos⁻¹ x) = x for x ∈ [-1, 1]

tan(tan⁻¹ x) = x for x ∈ (-∞, ∞)

Complementary angle relationships

sin⁻¹ x + cos⁻¹ x = π/2

tan⁻¹ x + cot⁻¹ x = π/2

sec⁻¹ x + csc⁻¹ x = π/2

Derivatives

d/dx[sin⁻¹ x] = 1/√(1 - x²)

d/dx[cos⁻¹ x] = -1/√(1 - x²)

d/dx[tan⁻¹ x] = 1/(1 + x²)

d/dx[cot⁻¹ x] = -1/(1 + x²)

d/dx[sec⁻¹ x] = 1/(|x|√(x² - 1))

d/dx[csc⁻¹ x] = -1/(|x|√(x² - 1))

Addition Formulas

sin⁻¹ x + sin⁻¹ y = sin⁻¹(x√(1-y²) + y√(1-x²)) [when x√(1-y²) + y√(1-x²) ≤ 1]

tan⁻¹ x + tan⁻¹ y = tan⁻¹((x+y)/(1-xy)) [when xy < 1]

Special Values

sin⁻¹(0) = 0, sin⁻¹(1/2) = π/6, sin⁻¹(1) = π/2

cos⁻¹(1) = 0, cos⁻¹(1/2) = π/3, cos⁻¹(0) = π/2

tan⁻¹(0) = 0, tan⁻¹(1) = π/4, tan⁻¹(√3) = π/3

Symmetry Properties

sin⁻¹(-x) = -sin⁻¹(x) (odd function)

cos⁻¹(-x) = π - cos⁻¹(x)

tan⁻¹(-x) = -tan⁻¹(x) (odd function)

Important Points Related to Inverse Trigonometric Functions

Students must keep the below-given pointers in mind to perform well in the exam. Be it your school exam or be it any entrance examination.

The value of an inverse trigonometric functions which lies in its principal value branch is called its principal values.
Principal value of inverse trigonometric functions is the least numerical value among all the values of that function.
Whenever no branch of an inverse trigonometric function is specifically mentioned the principal branch of the function should be taken.
The range of the inverse secant function is a restricted interval to ensure that the secant function is one-to-one and onto, allowing for the existence of an inverse.
The secant function is the reciprocal of the cosine function, so understanding the behaviour of the cosine function clarifies the secant function and its inverse.
The inverse secant function can be used to find the angle in a right triangle when the length of the hypotenuse and the adjacent side are known.
Inverse tangent is used in various fields like engineering, architecture, cartography, and marine biology to solve problems involving angles and ratios.
The inverse sine function is an increasing function within its defined domain, meaning as the input increases, the output also increases.
The inverse sine function is bounded between -π/2 and π/2, with the maximum value occurring at x = 1 (π/2) and the minimum value at x = -1 (-π/2).
The arccosine function is a decreasing function over its domain.
The graph of tan⁻¹(x) has vertical asymptotes at y = π/2 and y = -π/2, and its range is restricted to these asymptotes.
(12) The inverse cotangent function is strictly decreasing over its domain. As the input (x) increases, the output (y) decreases.
(13) Inverse trigonometric functions, including the inverse cotangent, are used in various fields like physics, engineering, and navigation to solve problems involving angles and trigonometric ratios.
(14) The sec⁻¹(x) function is strictly increasing on the interval (-∞, -1] and [1, ∞). As x increases, the angle given by sec⁻¹(x) also increases.
(15) The graph of sec⁻¹(x) has vertical asymptotes at x = -1 and x = 1. This is because the secant function approaches infinity at these points.
(16) The inverse cosecant function is a decreasing, odd function that maps the extended real line (excluding -1 to 1) to the interval (-π/2, π/2), excluding 0. It's closely related to the arcsine function and has key applications in trigonometry and calculus.
(17) The maximum value of cosec⁻¹(x) is π/2, occurring at x = 1. The minimum value is -π/2, occurring at x = -1.
(18) The maximum value of cosec⁻¹(x) is π/2, occurring at x = 1. The minimum value is -π/2, occurring at x = -1.