The Cartesian product helps us understand the relationship between values. It does nothing more than creating pairs between an element of one set and another. In CBSE Class 11, after moving from the basics of sets, your second chapter begins with the Cartesian products of sets to help you grasp relations and functions better.
Today, you will be learning a little more behind the Cartesian product meaning. This article dives into the properties and cardinality of Cartesian Products to prepare you for your JEE Mains. We also provide some relatable Cartesian product of sets examples, which should help when you are going through our expert-prepared NCERT Class 11 Maths Solutions.
- What Is a Cartesian Product
- Ordered Pairs: Why Does Order Matter
- How to Write a Cartesian Product Using Set Notation
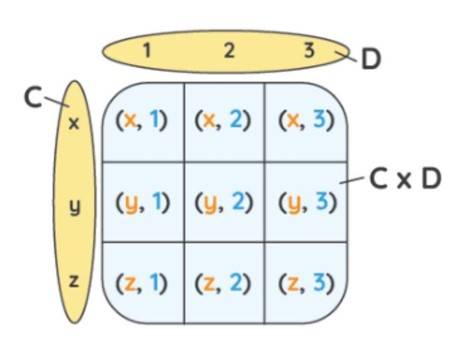
- Visualizing a Cartesian Product
- Properties of Cartesian Product
- Cardinality of a Cartesian Product
- Cartesian Product of Countable Sets
- Cartesian Product and Relations
- Real-Life Examples of Cartesian Product
- Conclusion
What Is a Cartesian Product
A Cartesian product is a way to combine elements of two sets to form ordered pairs. An ordered pair means the order of the elements matters. The result is a new set made up of all possible combinations of one item from each set.
Example:
Set
Set
Importance of Cartesian Products for Engineering Entrance Exams
- For engineering exams, it is expected that you know the core concepts and theoretical properties of the Cartesian products of sets.
- You may have to identify the different domains and the ranges of functions, for instance.
- Usually, in exams like the JEE Mains, the Cartesian products of sets is a foundation for set theory questions.
Ordered Pairs: Why Does Order Matter
In Cartesian products, order is very important. The pair ( ) is not the same as ( ), because the first element must come from the first set, and the second from the second set.
So:
, unless
How to Write a Cartesian Product Using Set Notation
This means: for every element in set and every element in set , we make a pair .
Visualizing a Cartesian Product
Example:
The cartesian product, also known as the cross-product or the product set of C and D is obtained by following the below-mentioned steps:
The first element is taken from the set and the second element 1 is taken from the second set
Both these elements are multiplied to form the first ordered pair (
)
The same step is repeated for all the other pairs too until all the possible combinations are chosen
The entire collection of all such ordered pairs gives us a cartesian product , .
Similarly, we can find the cartesian product of .
What About
?
Clearly,
Cartesian Product of More Than Two Sets
Example:
Cartesian Product with Empty Sets
If even one set is empty, the Cartesian product is empty.
Example:
and
Properties of Cartesian Product
Cardinality of a Cartesian Product
Cartesian Product of Countable Sets
If A and B are countable (even infinite), then A × B is also countable.
Cartesian Product and Relations
Real-Life Examples of Cartesian Product
Conclusion
Maths Relations and Functions Exam
Student Forum
Other Topics under this Chapter
- Antisymmetric Relation
- Composition of Functions and Invertible Function
- Types of Functions
- Types of Relations
- Relations and Functions
- Functions
- Cartesian Products of Sets
- Relations
- Linear Functions
- Beta Function
- Identity Function
- Difference between Relation and Function
- Composition of Functions
- Analytic Function
- Modulus Function
Other Class 11th Maths Chapters
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test