Pressure in Fluids: Class 11 Physics Notes, Definition, Working Principle, Formula & Real-Life Applications

When a fluid (either liquid or gas) is at rest, it exerts a force perpendicular to any surface in contact with it, such as a container wall or a body immersed in the fluid.

While the fluid as a whole is at rest, the molecules that makes up the fluid are in motion, the force exerted by the fluid is due to molecules colliding with their surroundings.

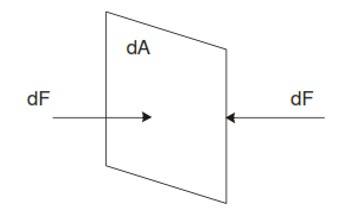
If we think of an imaginary surface within the fluid, the fluid on the two sides of the surface exerts equal and opposite forces on the surface, otherwise the surface would accelerate and the fluid would not remain at rest. Consider a small surface of area dA centered on a point on the fluid, the normal force exerted by the fluid on each side is . The pressure P is defined at that point as the normal force per unit area, i.e., $\mathrm{P}=\frac{\mathrm{d}\mathrm{F}}{\perp }\mathrm{d}\mathrm{A}$

If the pressure is the same at all points of a finite plane surface with area $A$ , then $P=\frac{F_{\perp }}{A}$

where ${\mathrm{F}}_{\perp }$ is the normal force on one side of the surface. The SI unit of pressure is pascal, where 1 pascal $=1\mathrm{P}\mathrm{a}=1.0\mathrm{N}/{\mathrm{m}}^2$
One unit used principally in meterology is the Bar which is equal to ${10}^5\mathrm{P}\mathrm{a}$

Note : Fluid pressure acts perpendicular to any surface in the fluid no matter how that surface is oriented. Hence, pressure has no intrinsic direction of its own, its a scalar. By contrast, force is a vector with a definite direction.
Atmospheric Pressure ( ${\mathbf{P}}_0$ )
It is pressure of the earth's atmosphere. This changes with weather and elevation. Normal atmospheric pressure at sea level (an average value) is $1.013\times {10}^5\mathrm{P}\mathrm{a}$
Absolute pressure and Gauge Pressure

The excess pressure above atmospheric pressure is usually called gauge pressure and the total pressure is called absolute pressure. Thus,

Gauge pressure = absolute pressure - atmospheric pressure

Absolute pressure is always greater than or equal to zero. While gauge pressure can be negative also.

Variation in pressure with depth
If the weight of the fluid can be neglected, the pressure in a fluid is the same throughout its volume. But often the fluid's weight is not negligible and under such condition pressure increases with increasing depth below the surface.
Let us now derive a general relation between the pressure $P$ at any point in a fluid at rest and the elevation $y$ of that point. We will assume that the density $\rho$ and the acceleration due to gravity $g$ are the same throughout the fluid. If the fluid is in equilibrium, every volume element is in equilibrium.
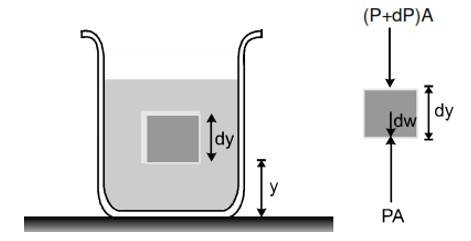
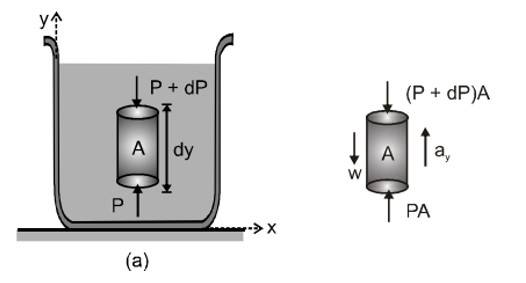
Consider a thin element of fluid with height dy. The bottom and top surfaces each have area A, and they are at elevations  and  above some reference level where $y=0$ . The weight of the fluid element is

$\mathrm{d}\mathrm{W}=($  volume $)$ (density) $\left(\mathrm{g}\right)=\left(\mathrm{A}d\mathrm{y}\right)\left(\rho \right)\left(\mathrm{g}\right)$

or $\mathrm{}dW=\rho gAdy$
What are the other forces in y-direction on this fluid element? Call the pressure at the bottom surface $P$ , the total $y$ component of upward force is $PA$ . The pressure at the top surface is $P+dP$ and the total $y$ -component of downward force on the top surface is $(P+dP)A$ . The fluid element is in equilibrium, so the total $y$ component of force including the weight and the forces at the bottom and top surfaces must be zero.

$\mathrm{\Sigma }{F}_y=0$

$\therefore \mathrm{}PA-(P+dP)A-\rho gAdy=0\mathrm{}$ or $\mathrm{}\frac{dP}{dy}=-\rho g$

This equation shows that when y increases, P decreases, i.e., as we move upward in the fluid pressure decreases.

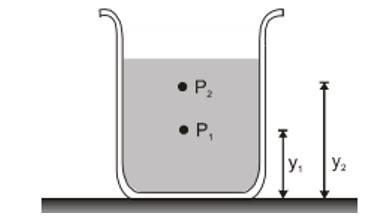
If $P_1$ and $P_2$ be the pressures at elevations $y_1$ and $y_2$ and if $\rho$ and $g$ are constant, then integration Equation (i), we get

or $P_2-P_1=-\rho g\left(y_2-y_1\right)$

It's often convenient to express Equation (ii) in terms of the depth below the surface of a fluid. Take point 1 at depth h below the surface of fluid and let P represents pressure at this point. Take point 2 at the surface of the fluid, where the pressure is ${\mathrm{P}}_0$ (subscript for zero depth). The depth of point 1 below the surface is, $\mathrm{h}={\mathrm{y}}_2-{\mathrm{y}}_1$

and equation (ii) becomes

$\begin{array}{rr}& P_0-P_{=}=-\rho g\left(y_2-y_1\right)=-\rho gh\\ \therefore & P=P_0+\rho gh\end{array}$

Thus pressure increases linearly with depth, if  and  are uniform. A graph between  and  is shown below.

Further, the pressure is the same at any two points at the same level in the fluid. The shape of the container does not matter.

The following methods are used for examining pressure in fluids:

1. Open Condition (like rivers or canals)

When the fluid is exposed to the air, like in a stream or an open tank, the top is just at regular air pressure. But if you go deeper into the water, pressure builds up—just because the water above is pushing down. I kinda think of it like when you're swimming: the deeper you dive, the more pressure you feel in your ears. People usually just measure how deep it is or use basic pressure tools to check.

2. Closed Condition (like pipes or tanks)

If the fluid is sealed in, like in a pipe or a tank, there's no open surface. That means the pressure can be higher—or even less—than normal air pressure. You’d need tools like piezometers (those vertical see-through tubes) or manometers to measure it. Sometimes they just use digital meters, depending on how the system is built.

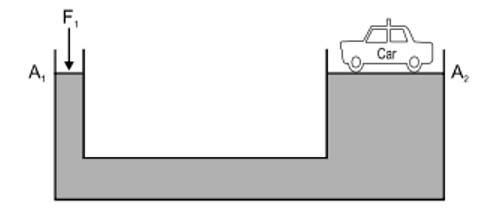
It states that "pressure applied to an enclosed fluid is transmitted undiminished to every portion of the fluid and the walls of the containing vessel".

A well known application of Pascal's law is the hydraulic lift used to support or lift heavy objects. It is schematically illustrated in figure.

A piston with small cross section area $A_1$ exerts a force $F_1$ on the surface of a liquid such as oil. The applied pressure $\mathrm{P}=\frac{{\mathrm{F}}_1}{{\mathrm{A}}_1}$  is transmitted through the connection pipe to a larger piston of area ${\mathrm{A}}_2$ . The applied pressure is the same in both cylinders, so $\mathrm{P}=\frac{{\mathrm{F}}_1}{{\mathrm{A}}_1}=\frac{{\mathrm{F}}_2}{{\mathrm{A}}_2}\text{or}{\mathrm{F}}_2=\frac{{\mathrm{A}}_2}{{\mathrm{A}}_1}\cdot F_1$

Now, since $A_2>A_1$ , therefore, $F_2>F_1$ . Thus hydraulic lift is a force multiplying device with a multiplication factor equal to the ratio of the areas of the two pistons. Dentist's chairs, car lifts and jacks, elevators and hydraulic brakes all are based on this principle.

1. At same point on a fluid pressure is same in all direction. In the figure, $P_1=P_2=P_3=P_4$

 

2. Forces acting on a fluid in equilibrium have to be perpendicular to its surface. Because it cannot sustain the shear stress.

3. In the same liquid pressure will be same at all points at the same level. For example, in the figure:

$\begin{array}{rr}& P_1\ne P_2\\ & P_3=P_4\text{and}{P}_5=P_6\end{array}$

Further ${\mathrm{P}}_3={\mathrm{P}}_4$

$\therefore P_0+{\rho }_{1}g{h}_1=P_0+{\rho }_{2}g{h}_2\text{or}{\rho }_1{h}_1={\rho }_2{h}_2\text{or}h\propto \frac{1}{\rho }$

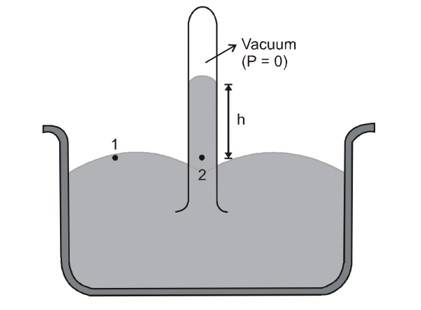
4. Torricelli Experiment (Barometer) :

It is a device used to measure atmospheric pressure .In principle any liquid can be used to fill the barometer, but mercury is the substance of choice because its great density makes possible an instrument of reasonable size.

Here, $\mathrm{}{P}_1=$ atmospheric pressure ( ${\mathrm{P}}_0$ ) and $\mathrm{}{P}_2=0+\rho gh=\rho gh$

$P_0=\rho gh$

Here $\mathrm{}\rho =$ density of mercury
Thus, the mercury barometer reads the atmosheric pressure $\left({\mathrm{P}}_0\right)$ directly from the height of the mercury column.
For example if the height of mercury in a barometer is 760 mm . then atmospheric pressure will be, $P_0=\rho gh=\left(13.6\times {10}^3\right)\left(9.8\right)\left(0.760\right)=1.01\times {10}^5\mathrm{N}/{\mathrm{m}}^2$

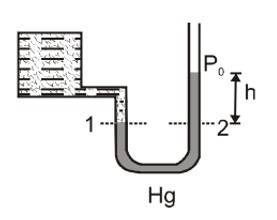
5. Manometer:

It is a device used to measure the pressure of a gas inside a container. The U- shaped tube often contains mercury

Here $\mathrm{}{P}_1=$ pressure of the gas in the container ( $P$ ) and $\mathrm{}{P}_2=$ atmospheric pressure $\left({\mathrm{P}}_0\right)+\rho gh$

This can also be written as $P-P_0=\text{gauge pressure}=\rho gh$

Here, $\rho$ is the density of the liquid used in $U$ - tube.
Thus by measuring $h$ we can find absolute (or gauge) pressure in the vessel.

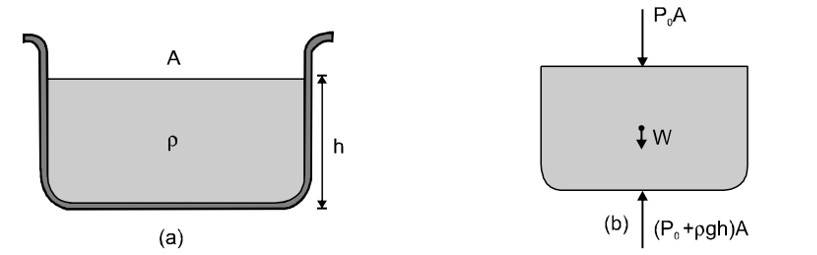
6. Free body diagram of a liquid :

The free body diagram of the liquid(showing the vertical forces only) is shown in fig (b) For the equilibrium of liquid.

Net downward force = net upward force

$\therefore \mathrm{}{P}_{0}A+W=\left(P_0+\rho gh\right)A\text{or}W=\rho ghA$

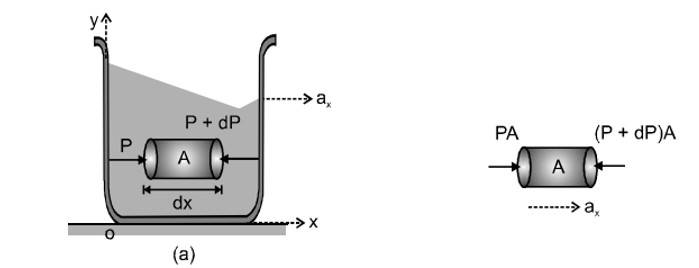
7. Pressure Difference in Accelerating Fluids

Consider a liquid kept at rest in a beaker as shown in figure (a). In this case we know that pressure do not change in horizontal direction (x-direction), it decreases upwards along y-direction So, we can write the equations,

$\frac{dP}{dx}=0\text{and}\frac{dP}{dy}=\rho g$

But, suppose the beaker is accelerated and it has components of acceleration $a_x$ and $a_y$ in $x$ and $y$ -directions respectively, then the pressure decreases along both $x$ and $y$ directions. The above equation in that case reduces to $\frac{dP}{dx}=-\rho a_x\text{and}\frac{dP}{dy}=-\rho \left(g+a_y\right)$

These equations can be derived as under. Consider a beaker filled with some liquid of density $\rho$ accelerating upwards with an acceleration $a_y$ along positive y-direction, Let us draw the free body diagram of a small element of fluid of area $A$ and length dy as shown in figure. Equation of motion for this element is, $PA-W-(P+dP)A=\left(\text{mass}\right)\left(a_y\right)\mathrm{}\text{or}\mathrm{}-W-\left(dP\right)A=\left(A\rho dy\right)\left(a_y\right)$

or $-\left(A\rho gdy\right)-\left(dP\right)A=\left(A\rho dy\right)\left(a_y\right)$ or $\frac{dP}{dy}=-\rho \left(g+a_y\right)$
Similarly, if the beaker moves along positive x -direction with acceleration ${\mathrm{a}}_{\mathrm{x}}$ , the equation of motion for the fluid element shown in figure is

$PA-(P+dP)A=($ mass $)\left(a_x\right)\mathrm{}$ or $-\left(dP\right)A=\left(A\rho dx\right)a_x\mathrm{}$ or $\mathrm{}\frac{dP}{dx}=-\rho a_x$

 

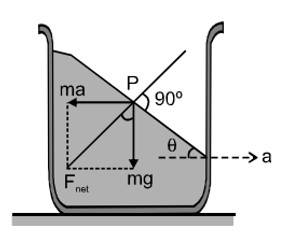
8. Free Surface of a Liquid Accelerated in Horizontal Direction

Consider a liquid placed in a beaker which is accelerating horizontally with an acceleration ' $a$ '. Let A and B be two points in the liquid at a separation $x$ in the same horizontal line. As we have seen in this case $dp=\rho adx\text{or}\frac{dP}{dx}=-\rho a$

Integrating this with proper limits, we get $P_A-P_B=\rho ax$
Furter $P_A=P_0+\rho g{h}_1$
and $\mathrm{}{P}_B=P_0+\rho g{h}_2$
substituting in Eq. (iii) we get

$\begin{array}{rr}& \rho g\left(h_1-h_2\right)=\rho ax\\ & \frac{h_1-h_2}{x}=\frac{a}{g}=\mathrm{t}\mathrm{a}\mathrm{n}\theta \\ & \mathrm{t}\mathrm{a}\mathrm{n}\theta =\frac{a}{g}\end{array}$

Alternate Method

Consider a fluid particle of mass  at point  on the surface of liquid. From the accelerating frame of reference, two forces are acting on it,

(i) Pseudo force(ma)

(ii) Weight (mg)

As we said earlier also, net force in equilibrium should be perpendicular to the surface.

$\therefore \mathrm{t}\mathrm{a}\mathrm{n}\theta =\frac{\mathrm{m}\mathrm{a}}{\mathrm{m}\mathrm{g}}\text{or}\mathrm{t}\mathrm{a}\mathrm{n}\theta =\frac{\mathrm{a}}{\mathrm{g}}$

The following factors affect the pressure in fluids:

1. Depth of the Fluid: As you go deeper into a fluid, the pressure increases. That’s because the fluid above is adding its weight, pressing down on the layers below. The deeper you go, the more weight there is on top.
2. Density of the Fluid: Fluids with more mass packed into the same space (like mercury or oil) create more pressure. At the same depth, a denser fluid will push harder than a lighter one. So, pressure isn't just about depth—it’s also about what’s in the fluid.
3. Gravity (Gravitational Acceleration): Gravity pulls the fluid down, which is what creates the pressure in the first place. If gravity is stronger (like on Jupiter), the pressure builds up faster with depth. So, the same fluid would feel heavier under stronger gravity.
4. Atmospheric Pressure: If the fluid is open to the air, the atmosphere pushes down on its surface. This adds to the pressure already in the fluid from its own weight. That’s why fluid pressure near the surface isn’t always zero—it starts from the air pressure above.