If you have wondered how heavy a thing like an aeroplane glides smoothly over the sky, it’s the Bernoulli’s Principle at play. It’s the reason why the plane’s wings are designed in a particular shape - curvy top with a flat bottom.
With that, air can move faster over the curved top for lower pressure and slower under the flat bottom for higher pressure. This pressure difference - low above and high under the wings - creates an upward force that lets the plane stay in the air.
Now, if you just got started with your Mechanical Properties of Fluids chapter, you read about Pressure of Fluids and Pascal’s Law already. This chapter also has the Bernoulli’s Principle to show you how it’s a powerful model to understand fluid behaviour. In the coming sections, we will have the Bernoulli’s Principle explained more in detail, so that you are answering correctly about this section in your upcoming JEE Mains or similar entrances.
- What is Bernoulli's Principle?
- What is the Bernoulli’s Equation?
- Bernoulli’s Principle Formula Derivation
What is Bernoulli's Principle?
Bernoulli’s Principle shows an inverse relationship between velocity and pressure of a moving fluid. This is a fundamental principle of fluid dynamics, stating that when the flow of a moving fluid increases, the pressure within it decreases, or vice versa.
So, considering air as a fluid here, you can remember like this
Faster air = Lower air pressure
Slower air = Higher air pressure
What is the Bernoulli’s Equation?
The Bernoulli’s equation follows or derives from the Law of Conservation of Energy.
Think of this law that applies to fluids in this case, where a fluid's total mechanical energy (pressure + kinetic + potential) remains constant.
So, as L. J. Clancy, in his book, Thermodynamics shows a way to memorise Bernoulli’s Principle through a simple equation
Static pressure + Dynamic pressure = Total pressure
The basic formula for Bernoulli’s Principle is
Conditions for Bernoulli's Principle
One of the primary conditions for Bernoulli’s Principle to work is that the fluid must be ideal.
That means the fluid cannot have any friction when flowing. You can think of water that does not have any friction when flowing, and compare that with thick syrup that has friction.
Secondly, the fluid’s volume should not change under pressure. If the fluid were compressible, the density would change. In Bernoulli’s equation, the pressure is treated as constant.
Third condition. To understand Bernoulli’s Principle, the only gravity can affect the fluid.
Master gravitational concepts with NCERT Solutions for Gravitation and score high in your annuals!
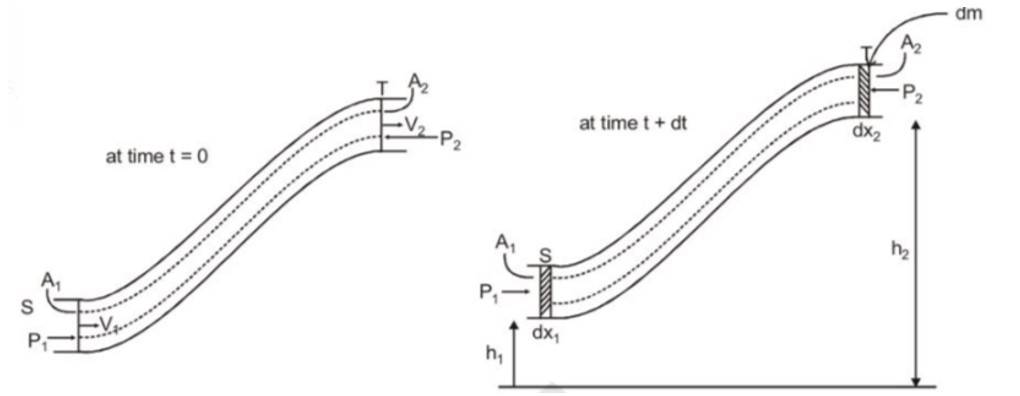
Bernoulli’s Principle Formula Derivation
The derivation of Bernoulli’s Principle equation can be based on the Work-Energy Theorem. This states that the net work done = Change in Kinetic Energy + Change in Potential Energy.
Let’s try to understand the energy changes in a flowing fluid, while you can read about Work in Physics and prepare for your next chapters for your upcoming tests and exams.
You can consider a small mass dm1 of fluid entering at point S.
Its mass is
where A1dx1 is the volume dV1.
Once this fluid enters S, the surrounding pressure P1 does work on the fluid. The calculation is
At the same time the amount of fluid moves out of the tube at point is
So, the equation of continuity goes like
The work done in the displacement of mass at point T
After we apply the Work Energy Theorem, we get
Physics Mechanical Properties of Fluids Exam
Student Forum
Other Topics under this Chapter
Other Class 11th Physics Chapters
- Physics Mechanical Properties of Solids
- NCERT Class 11 Physics
- NCERT Class 11 Notes
- NCERT Notes
- Physics Motion in Plane
- Physics Mechanical Properties of Fluids
- Physics Motion in Straight Line
- Physics System of Particles and Rotational Motion
- Physics Oscillations
- Physics Waves
- Physics Thermal Properties of Matter
- Physics Motion
- Physics Gravitation
- Physics Thermodynamics
- Physics Work, Energy and Power
- Physics Units and Measurement
- Physics Laws of Motion