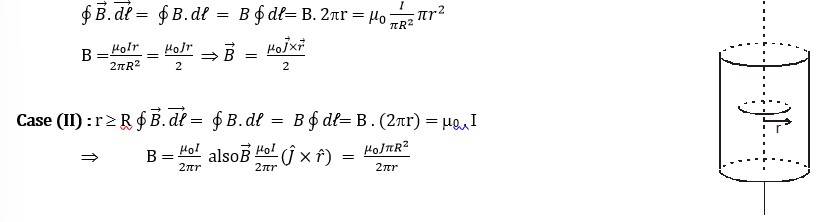Ampere's Circuital Law: Class 12 Physics Notes, Definition, Working Principle, Formula & Real-Life Applications

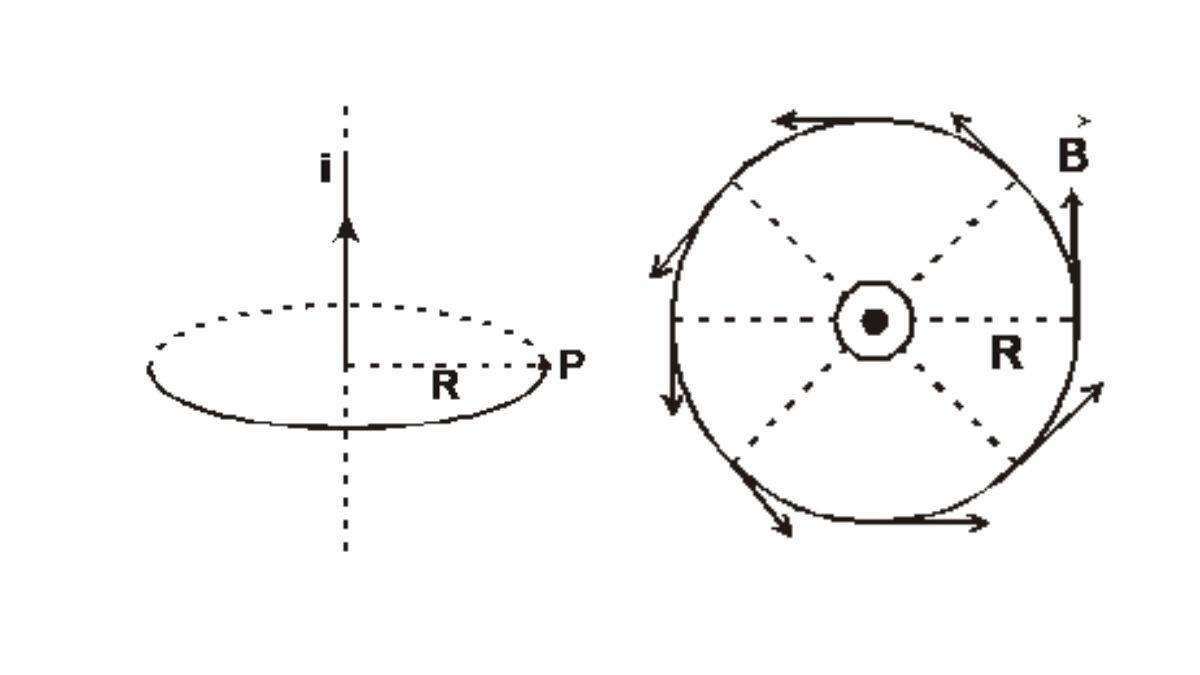
The line integral $\oint \vec{B}\cdot \overrightarrow{d\mathcal{l}}$  on a closed curve of any shape is equal to m₀ (permeability of free space) times the net current I through the area bounded by the curve.

$\text{∮}\mathrm{}\vec{\mathrm{B}}\cdot \overrightarrow{\mathrm{d}\mathcal{l}}={\mu }_0\mathrm{I}$

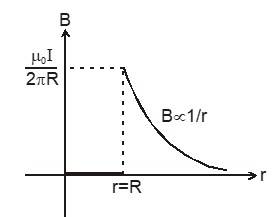
Uses :  To find out magnetic field due to infinite current carrying wire       

                                                               

$$\text{By B.S.L.}\vec{B}\text{will have circular lines.}\overrightarrow{dl}\text{is also taken tangent to the circle.}$$

$\oint \vec{B}.\overrightarrow{d\mathcal{l}}\mathrm{}=\oint B.d\mathcal{l}$     Θ = 0º so B d $\oint d\mathcal{l}$ = B 2πR   ( B = const.)

Now by Ampere's law : B 2πR =  B = $\frac{{\mu }_{0}i}{2\pi R}$

Historical Development of Ampere's Circuital Law

In the early 1800s, Hans Ørsted ran a current through a wire and noticed a compass needle shift. That observation opened the door. It told scientists, wait—electricity can affect magnetism?

Then Ampère took it further. He didn’t just observe the effect—he measured it. He showed that electric current and magnetic fields were directly related. His work gave us the law named after him.

Later, Maxwell realized Ampère’s version had a blind spot. In situations where the electric field changed, the math didn’t hold up. So he added what we now call displacement current to fix it. That update turned Ampère’s Law into one of the four Maxwell equations—cornerstones of electromagnetism.

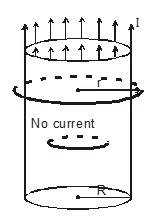
Hollow Current Carrying Infinitely long cylinder

I is uniformly distributed on the whole circumference

(i) for r > R

By symmetry the amperian loop is a circle.

1. $\oint \vec{B}.\overrightarrow{d\mathcal{l}}=\mathrm{}\oint B.d\mathcal{l}$ Θ = 0

b.  B = $B\underset{0}{\overset{2\pi r}{\int }}d\mathcal{l}$ B=const => B= $\frac{{\mu }_0{\rm I}}{2\pi r}$

(ii) r < R = $\oint \vec{B}.\overrightarrow{d\mathcal{l}}\mathrm{}=\mathrm{}\oint B.d\mathcal{l}$                 

= B(2πr) = 0 => B_in = 0

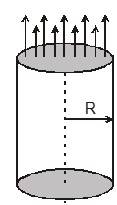
Solid Infinite Current Carrying Cylinder

Assume current is uniformly distributed on the whole cross section area

current density J = $\frac{{\rm I}}{\pi R^2}$

Case (I) : r ≤ R                                                                                                                                   

take an amperian loop inside the cylinder. By symmetry it should be a circle whose centre is on the axis of cylinder and its axis also coincides with the cylinder axis on the loop.

There are basically two ways to write this law:

Integral Form: This is the loop version, the one we’ve seen already. Great for symmetrical cases where you can walk a loop around a current.
$$\text{Differential Form:}\text{More precise, used when we want to know how the magnetic field behaves at every point in space.}\text{Written as}\nabla \times \vec{B}={\mu }_0\vec{J}\text{, where}\vec{J}\text{is current density.}$$

Which one you use depends on the situation. For simple loops and wires, stick with the integral. For more complex systems, the differential form is your friend.

Do remember that this chapter is also important for CBSE Board exam and NEET exam. 

When an electric current flows, it generates a magnetic field around it. If you curl your right hand’s fingers around a wire with your thumb pointing in the direction of the current, your fingers show the direction of the magnetic field. The law lets us calculate how strong that magnetic field is, depending on the current and the distance from the wire, or any shape that the current takes. It’s like mapping out invisible lines that loop around the wire.

$$\text{1. Long Straight Wire}\text{Say you’ve got an infinitely long wire carrying current}I\text{. Using a circular loop around it (same distance all around), the magnetic field comes out to:}B=\frac{{\mu }_{0}I}{2\pi r}\text{2. Solenoid}\text{In a solenoid with tightly packed coils, the magnetic field inside is nearly uniform. For}n\text{turns per meter and current}I\text{:}B={\mu }_{0}nI\text{3. Toroid}\text{A toroid is like a solenoid bent into a doughnut shape. The field inside, at a radius}r\text{from the center:}B=\frac{{\mu }_{0}NI}{2\pi r}$$ $$\text{1. Long Straight Wire:}\text{Say you’ve got an infinitely long wire carrying current}I\text{Using a circular loop around it (same distance all around), the magnetic field comes out to:}B=\frac{{\mu }_{0}I}{2\pi r}$$ $$\text{2. Solenoid:}\text{In a solenoid with tightly packed coils, the magnetic field inside is nearly uniform.}\text{For}n\text{turns per meter and current}I\text{:}B={\mu }_{0}nI$$ $$\text{3. Toroid:}\text{A toroid is like a solenoid bent into a doughnut shape. The field inside, at a radius}r\text{from the center:}B=\frac{{\mu }_{0}NI}{2\pi r}$$

1. Take electromagnets, for example. You have got a coil of wire, you run current through it, and you get a magnetic field. This happens because Ampere’s Law is doing the work. The stronger the current, the stronger the field. Engineers use it to decide how many turns the coil needs, how much current to use, and what kind of core to stick in the middle (like iron).
2. Now, take inductors. These are coils of wire used in all kinds of electronic circuits, and their main job is to store energy, but not in the way a battery does. They store it in the magnetic field that forms when current flows through the coil. What’s interesting is how that field depends entirely on the current and the way the wire is arranged. If the current suddenly changes, the inductor pushes back a bit, trying to keep the magnetic field steady. That’s where Ampere’s Law comes in — it helps you figure out how strong that magnetic field will be and how it wraps around the coil.
3. Transformers shift voltages up or down in power lines and electronics. If you want them to work right, you’ve got to know how the magnetic field flows through that iron core. And how much field you get depends on the current in the wire coils. That’s exactly the kind of thing Ampere’s Law helps you figure out.

This law isn’t just a piece of theory—it’s used all over the place. Engineers lean on it when designing inductors, electromagnets, or even complex circuits. It helps predict how magnetic fields behave when currents flow through different shapes.

And for students or physicists? It offers a shortcut. When the current distribution has some symmetry—like in wires or solenoids, you do not need to have the knowledge of complex equations since Ampere’s Law simplifies it.

Plus, it forms part of the bigger picture. It is one of Maxwell’s equations, meaning it plays a role in explaining light, radio waves, and more