Torque on Current Loop, Magnetic Dipole: Class 12 Physics Notes, Formula, Applications & Significance

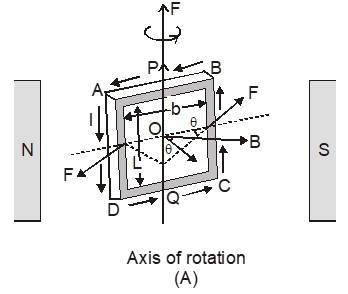
When a current-carrying coil is placed in a uniform magnetic field, the net force on it is always zero. However, as its different parts experience forces in different directions so the loop may experience a torque (or couple) depending on the orientation of the loop and the axis of rotation. For this, consider a rectangular coil in a uniform field B which is free to rotate about a vertical axis PQ and normal to the plane of the coil, making an angle q with the field direction as shown in Figure (A).

 

The arms AB and CD will experience forces B(NI)b vertically up and down, respectively. These two forces together will give zero net force and zero torque (as they are collinear with the axis of rotation), so they will have no effect

on the motion of the coil.

Now the forces on the arms AC and BD will be BINL in the direction out of the page and into the page, respectively, resulting in zero net force, but an anticlockwise couple of value

t = F × Arm = BINL × (b sinΘ)

i.e.   t = BIA sinΘ with A = NLb        ......(i)

 

Now treating the current–carrying coil as a dipole of moment $\vec{M}={\rm I}\vec{A}$ Eqn. (i) can be written in vector form as $\vec{\tau }=\vec{M}\times \vec{B}\mathrm{}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{}\vec{M}={\rm I}\vec{A}=N{\rm I}A\vec{n}$ ......(ii)

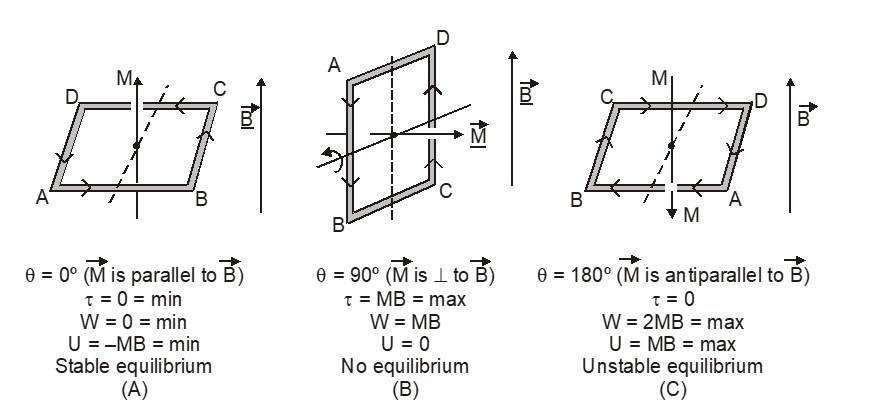
This is the required result, and from this it is clear that :

(1) Torque will be minimum (= 0) when sinq = min = 0, i.e., q = 0º, i.e. 180º, i.e., the plane of the coil is

perpendicular to the magnetic field, i.e. normal to the coil is collinear with the field [fig. (A) and (C)]

 

(2) Torque will be maximum (= BINA) when sinΘ = max = 1, i.e., q = 90º, i.e. the plane of the coil is parallel to

the field, i.e. normal to the coil is perpendicular to the field. [fig.(B)].

                 

(3) By analogy with a dielectric or magnetic dipole in a field, in the case of current–carrying in a field.

U = – $\vec{M}•\vec{B}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{}\mathrm{F}\mathrm{}=\mathrm{}–\frac{dU}{dr}$

and W = MB(1 – cosΘ)

The values of U and W for different orientations of the coil in the field are shown in fig.

(4) Instruments such as electric motor, moving coil galvanometer and tangent galvanometers, etc. are based

on the fact that a current–carrying coil in a uniform magnetic field experiences a torque (or couple).

A magnet always has two poles ‘N’ and ‘S’ and like poles of two magnets repel each other and the unlike poles of two magnets attract each other they form action reaction pair.

The poles of the same magnet do not come to meet each other due to attraction. They are maintained we cannot get two isolated poles by cutting the magnet from the middle. The other end becomes pole of opposite nature. So, ‘N’ and ‘S’ always exist together.

They are known as +ve and –ve poles. North pole is treated as positive pole (or positive magnetic charge) and the south pole is treated as –ve pole (or –ve magnetic charge). They are quantitatively represented by their ”POLE STRENGTH” +m and –m respectively (just like we have charges +q and –q in electrostatics). Pole strength is a scalar quantity and represents the strength of the pole hence, of the magnet also).

                 

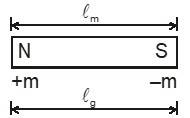
A magnet can be treated as a dipole since it always has two opposite poles (just like in electric dipole we have two opposite charges –q and +q). It is called MAGNETIC DIPOLE and it has a MAGNETIC DIPOLE MOMENT. It is represented by $\vec{M}$ . It is a vector quantity. It’s direction is from –m to +m that means from ‘S’ to ‘N’)

M = m.l_m here l_m = magnetic length of the magnet. l_m is slightly less than l_g (it is geometrical length of the magnet = end to end distance). The ‘N’ and ‘S’ are not located exactly at the ends of the magnet. For calculation purposes we can assume l_m = l_g [Actually l_m/l_g  ~ 0.84].

The units of m and M will be mentioned afterwards where you can remember and understand.

Below are the application and significance of the Current Loop and the Magnetic Dipole 

Application: 

• Electric Motors 

• Generator 

• Magnetic Storage 

Significance 

• Energy conversion 

• Foundation of Electromagnetism