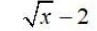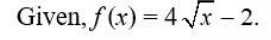The subject matter experts at Shiksha created the Class 11 Limits and Derivatives NCERT solutions. The chapter introduces Calculus, a branch of mathematics that studies the change in the value of a function as the points in the domain change. Limits and Derivatives class 11 Chapter 12 Maths includes the definitions of limits and derivatives and some algebra involving these concepts.
The step-by-step solutions help students to understand the concepts clearly and also provide them the confidence to appear in their school exam, CBSE Board exam, and other entrance tests later on. These solutions are accurate, and students can depend on them for their exam preparation. If they practiced only from these solutions, after going through the NCERT chapter, it would be more than sufficient for their examination preparation.
For comprehensive subject-wise NCERT notes of Class 11 and Class 12, Check Here. You will get the reliable notes for quick revision.
Related Links
| NCERT Solutions for Class 11 Maths | NCERT Class 11 Notes | NCERT Solutions Class 11 and 12 for Maths, Physics, Chemistry |
- Class 11 Maths Chapter 12 Snapshot: Limits and Derivatives
- Class 11 Math Limits and Derivatives: Key Topics, Weightage
- Important Formulas of Class 11 Limits and Derivatives
- Class 11 Maths Chapter 12 NCERT Solutions – Limits and Derivatives PDF Free
- Class 11 Math Limits and Derivatives Exercise-wise Solution
- Class 11 Math Limits and Derivatives Exercise 13.1 Solution
Class 11 Maths Chapter 12 Snapshot: Limits and Derivatives
Here is a quick summary of the Limit and Derivatives Class 11 Maths:
- According to Chapter 12 of Class 11 Maths, is the expected value of f, which is called the left-hand limit of f at a, when x=a. Here, it is given that the values of f near x to the left of a.
- To find the right-hand limit of f(x) at a, mathematically we show as - . It is the expected value of f at x = a, given the values of f near x to the right of a.
- There is also the concept of common value when the right and left-hand limits coincide. It is denoted by .
To get access to the chapter-wise Class 11 Maths NCERT Notes that offer solved examples and also provide the important topics, students must check here.
Class 11 Math Limits and Derivatives: Key Topics, Weightage
Limits Class 11 Maths Chapter 12 is the part of the broader "Limits, Continuity & Differentiability" topic in the JEE Main exam. Hence, the students must focus on the core concepts of the chapter. Before starting the preparation of the chapter, it is wise to know the topics of this chapter. See below the topics covered in this chapter:
| Exercise | Topics Covered |
|---|---|
| 12.1 | Introduction |
| 12.2 | Intuitive Idea of Derivatives |
| 12.3 | Limits |
Class 11 Limits and Derivatives Weightage in JEE Main Exam
| Exam | Number of Questions | Weightage |
|---|---|---|
| JEE Main | 1 to 3 questions | 3.3% to 10% |
Important Formulas of Class 11 Limits and Derivatives
Important Formulae of Limits and Derivatives for CBSE and Competitive Exams
- First Principle of Differentiation
- Power Functions:
- Trigonometric Functions:
- Exponential & Logarithmic Functions:
-
Rules of Differentiation
- Sum Rule:
- Difference Rule:
- Product Rule:
- Quotient Rule:
- Chain Rule:
- Sum Rule:
Class 11 Maths Chapter 12 NCERT Solutions – Limits and Derivatives PDF Free
If students download the free Limits and Derivatives Class 11 PDF from the link given below, they will get the well-structured solutions of all the NCERT questions of chapter 12 Class 11 Maths. It will help them to do well in school exam, CBSE, and the JEE Main exam.
Chapter 5 Limits and Derivatives Class 11 NCERT Solutions: Download PDF for Free
Class 11 Math Limits and Derivatives Exercise-wise Solution
Class 11th Math Limits and Derivatives helps students understand the fundamentals of calculus unit, including differentiation, application of derivatives, integral and more. There are various important topics in this chapter such as checking differentiability, continuity, derivatives of different functions, and more. Limits and Derivatives Class 11 Solutions will include solution of all the exercises in lucid language. Ex 13.1 Class 11 will include problems related to the basic concepts of Limits and Derivatives such as using limit, finding continuity and differentiability. Class 11 Math Ex 13.2 includes more concepts such as finding derivatives of various functions and using them as application. Miscellaneous exercise covers various topics covered throughout the chapter. Students can check all the solutions below;
Class 11 Math Limits and Derivatives Exercise 13.1 Solution
Limits and Derivatives Exercise 13.1 focuses on fundamentals of the Limits. Student will be able to understand the application of limit to find first derivative of the given function for a given range. Ex 13.1 Class 11 Math in the Limits and Derivatives includes problems based on trigonometric functions, algebraic functions and exponential functions and finding their first derivative using the limits. Class 11 Math Ex 13.1 solution will contain solution of all 32 short and long answer type questions. Students can check the solutions below;
Class 11 Math Limits and Derivatives Exercise 13.1 NCERT Solution
| Q1. x+ 3 |
| A.1. x + 3 = 3 + 3 = 6. |
| Q2. |
| A.2. |
| Q3. |
| A.3. |
| Q4. |
| A4. |
Commonly asked questions
40. Find the derivative of for some constant a.
40. Given, f(x)=
So,
42. Find the derivative of the following functions:
(i)sin x cos x (ii) (iii)5 sec x + 4 cosx
(iv) (v)3cot x + 5 cosec x
(vi) (vii)
(i) f(x)=sin x cos x
So,
So,
(iii) Given f(x)=5 sec x+4 cosx.
So,
(v) Given,f(x)=3 cot x+5cosecx.
So,
52.
Kindly consider the following
52. Given, f (x) =
59.
Kindly consider the following
59. Given, f (x) =
So, f?(x) =
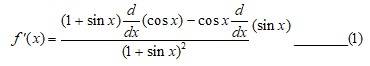
Putting (2) and (3) in (1) we get,
66.
Kindly consider the following
(x2 + 1) cos x
66. Given, f (x) = (x2 + 1) cos x
f? (x) = (x2 + 1)
= x2 sin x sin x + 2x cos x.
Kindly consider the following
68. (x + cos x) (x tan x)
68. Given, f (x) = (x + cos x) (x tan x)
So, f?(x) = (x + cos x)
Let g (x) = tan x.
So, g?(x) = 
= sec2x ______ (2)
Put (2) in (1) we get,
f?(x) = (x + cos x) (1 - sec2x) +(1 - sin x) (x- tan x)
We know that,
1 + tan2x = sec2x
Þ 1 - sec2x = - tan2x
So, f?(x) = - tan2x(x + cos x) +(x- tan x) (1 - sin x).
17. Kindly consider the following
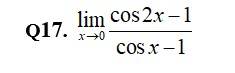

= 4
30. If For what value (s) of a does exists?
30. Given,
As | x | =
We can rewrite f (x) =
Case 1: when a<0,
So, = exist such that a< 0
Case II when a> 0,
So, exist such that a>0.
Case III when a = 0.
L.H.L =
R.H.L =
Thus,
So, does not exist at a = 0.
22.
22.
Put y = x . So that as y 0 cos
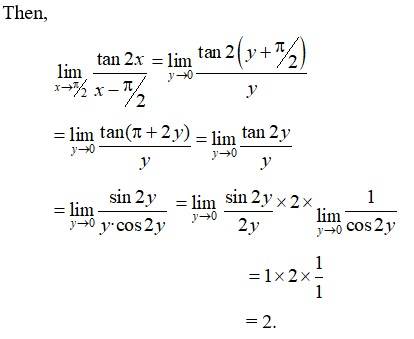
12.
Kindly go through the solution
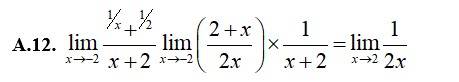
10
10.
We know that,
So,
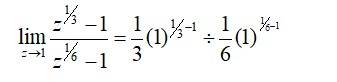
6.
6.

| Q6. |
6.  (0)4 + 5(0)3 + 10(0)2 + 10(0) + 5 = 5. |
Kindly consider the following
71.
71. Given, f (x) =
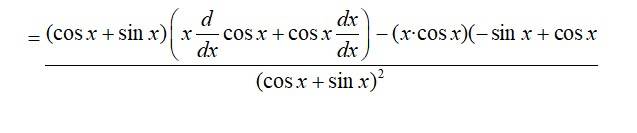
Dividing numerator and denominator by cos2x we get,
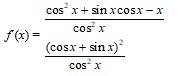
1. l x+ 3
Exercise 13.1
1. 1. x + 3 = 3 + 3 = 6.
7.
7. 
9.
Kindly go through the solution
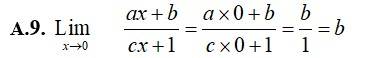
18.
18.
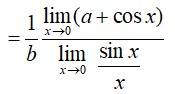
16.
16.
15.
15.
8.
8. 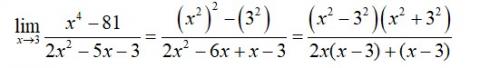
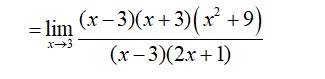
14.
14.

19.
19.
= 0.
4.
4.
5.
5.
21.
21.
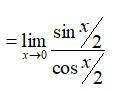
2.
2.
3.
3.
11.
11.
13.
13.
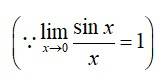
20.
20.
= 1.
23. Find and , where f (x)
23. Given f (x)
for
left hand limit, L.H.S = =
= 2 0 + 3 = 3.
Right hand limit, R.H.L =
= (0 + 1) = 3 1 = 3.
Thus,
For
L.H.L =
R.H.L =
Thus,
24. Find , where
24. Given
Now, L.H.L =
12- 1 = 0
And R.H.L = (1)2 1 = 1 = 2.
Thus,
So, does not exist.
25. Evaluate where f (x) =
25. Given f (x) =
We know that,
Now,
L.H.L =
and R.H.L =
Thus,
i e, does not exist.
26. Find wheref (x)
26. Given, f (x)
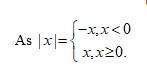
L.H.S =
R.H.L
Thus,
i e, does not exist.
27.Find f (x)
27.
= | 5 | 5
= 5 5
= 0
28. Supposef (x) = and if = f (1) what are possible values of a and b?
28. Given, f (x) =
Since we need we need,
LHL =
= a + b × 1 = a + b
and RHL =
= b - a × 1 = b - a
Given, we have the following equations
a + b = 4 ____ (1)
b - a = 4 ____ (2)
Adding (1) and (2) we get,
2b = 8
b = 4
Putting b = 4 in (1) we get
a + 4 = 4
a = 0
31. If the function f(x) satisfies , evaluate
31. Given,
39. For some constants aand b, find the derivative of
(i) (x- a) + (x - b) (ii) (iii)
(c) Given, f(x)=(x-a)(x-b)
where a and b are constants.
So,
=(x-a)+(x-b)
= 2x– a- b.
(ii) Given f(x)= where ab are constant
So,
=
=
(iii) Given, f(x)= where a and bare constants
So,
41. Find the derivative of
(i) (ii)
(iii) (iv)
(v) (vi)
41. (i)
=2.
(ii) Given, f(x)=
So,
=
(iii) Given, f(x) =
So,
(iv) Given, f(x)=
=
(v) Given, f(x)=
So,
(vi) Given, f(x)=
So,
44. Find the derivative of the following functions from first principle:
(i) x (ii) (x)1 (iii) sin(x + 1) (iv) cos
Find the derivative of the following functions (it is to be understood that a, b, c, d,
p, q, r and s are fixed non-zero constants and m and n are integers):
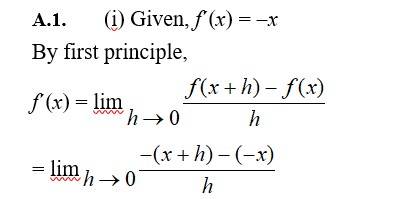
= - 1.
(ii) Given, f(x) = (-x)-1
by first principle,
f(x)
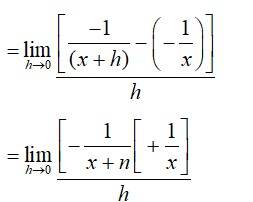
(iii) Given, f(x) = sin(x + 1)
By first principle,
f’(x) =
= cos (x + 1)
(iv) Given, f(x) = cos
By first principle,
f(x) =
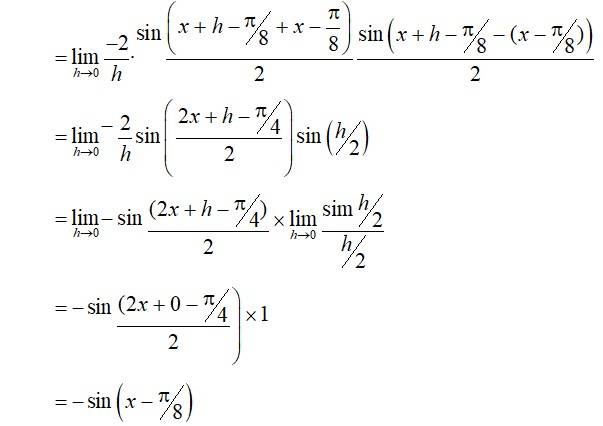
48.
Kindly consider the following
48. Given, f (x) =
So, f? (x) =
54.
Kindly consider the following
60.
Kindly consider the following
60. Given, f (x) =
So, f?(x) =
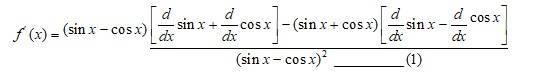
Let g(x) = cos x and p(x) = sin x.
{from so g’(x) A ) (upto equation 3)
Let g(x) = cos2 and p(x) = sin x.
So, g?(x) =

= -sin x ______ (2)
And p?(x) =
= cos x _____ (3)
Putting (2) and (3) in (1) we get,
61.
Kindly consider the following
61. Given, f (x) =
So, f?(x) =
Let g(x) = cos x.
So, g?(x)
= -sin x.
So, f?(x)
64.
Kindly consider the following
64. Given, f (x) =
Let g?(x) = sin (x + a)
So, g?(x) =
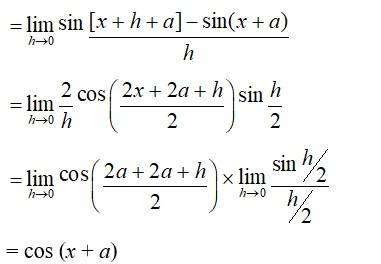
= cos (x + a)
And P(x) = cos x
So, P?(x) =
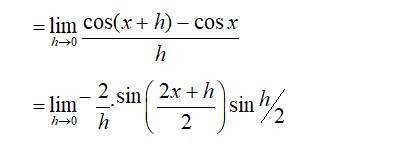
Thus, f?(x) =
66.
Kindly consider the following
x4 (5 sin x 3 cos x)
65. Given, f (x) = x4. (5 sin x 3 cos x)
As
and
Thus,
Kindly consider the following
70.
70. Given, f (x) =
So, f? (x) = 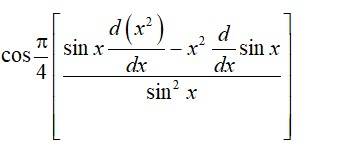
Kindly consider the following
72. (x + sec x) (x- tan x
72. Given, f (x) = (x + sec x) (x tan x)
So, f?(x) = (x + see x)
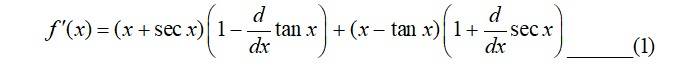
Let g(x) = tan x.
So, g?(x) = ![]()
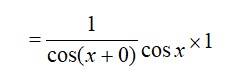
. _____ (2)
And P(x) = see x.

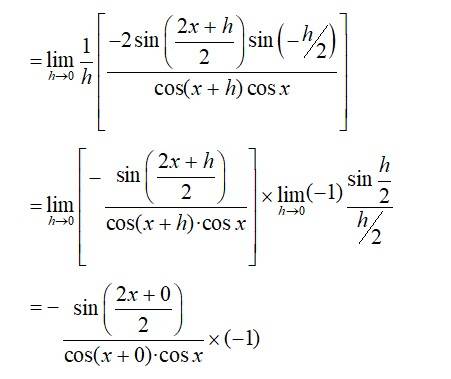
= tan x sec x. ____ (3)
Putting (2) and (3) in (1) we get,
f?(x) = (x + sec x) (1 - sec2x) + (x- tan x) (1 + tan x sec x)
Kindly consider the following
73.
73. Given, f (x) =
So, f?(x) =
=
32. If f (x) = . For what integers m and n does both and exist?
32. Given, f (x) =
For
n = m
So, exist for n = m.
Again,
So, Thus, exist for any integral value of m and n.
33. Find the derivative
33. Given, f (x)=x2- 2 .,
We have,
=
=
=20
34. Find the derivative of x at x = 1.
34. Given, f (x)=x, f (1)=?
We have,
=1
35. Find the derivative of 99x at x = l00
35. Given, f (x)= 99x, f (100)=?
So, f (100)=
=99
36. Find the derivative of the following functions from first principle.
36. (i) (ii) (x -1)(x-2)
(iii) (iv)
A.4.(i) Given,
So,
=0+3 x(x+ 0)
=3x2
(ii) Given, f(x) =(x-1)(x-2)
=x2- 3x+2
So,
=
=
= 2x – 3.
(iii) Given, f(x)=
So,
(iv) Given, f(x)=
37. For the function
Prove that
37.
Given
At x=0,
f(X) =1.
and at x=1,
=100 1
=100
Hence,
38. Find the derivative of for some fixed real number a.
38. Given,
We know that,
So,
42. Find the derivative of cos x from first principle.
42. Given, f(x) = cos x
By first principle,
47. (ax + b) (cx + d)2
47. Given, f (x) = (ax + b) (cx + d)2
So, f?(x) = (ax +b)
48.
Kindly consider the following
48. Given, f (x) =
So, f (x) =
49.
Kindly consider the following
49. Given, f (x) =
So, f (x) =
=
51.
Kindly consider the following
51. Given, f (x) =
So, f(x) =
53.
Kindly consider the following
53. Given, f (x) =
So, f(x) =
55.
Kindly consider the following
(ax + b)n
55. Given, f (x) = (ax + b)n
Chain rule, where
u (x) is a function of x.
So, f (x) =
56. (ax + b)n (cx + d)m
56. Given, f (x) = (ax + b)n (cx + d)m
So, f’(x) =
57.
Kindly consider the following
sin(x + a)
57. Given, f (x) = sin (x + a)
So, f (x) =
= cos (x + a)
58.
Kindly consider the following
cosec x. cot x
58. Given f (x) = cosec x. cot x.
By Leibnitz product rule,
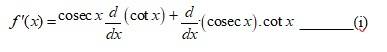
So, g(x) =
= -cosec2x.______(2)
And hx) =
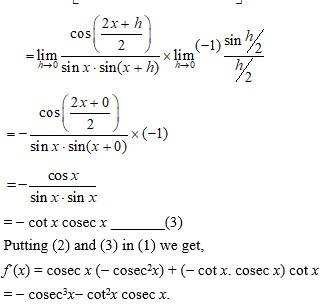
63.
Kindly consider the following
63. Given, f (x) =
f?(x) =
{Copy (A)}
So, g?(x) =
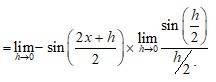
= sin x ______ (2)
And p?(x) =
= cos x _____ (3)
So, put (2) and (3) in (1) we get,
62.
Kindly consider the following
sinnx
62. Given, f (x) =sinnx
By chain rule,
f? (x) = n (sin x)n-1 sin x
Let (gx) = sinx
So, g? (x)
=
= cos x.
So, f? (x) = n (sin x)n-1 cos x.
67.
Kindly consider the following
(ax2 + sin x) (p +q cos x)
67. Given, f (x) = (ax2 + sin x) (p +q cos x).
So, f? (x) = (ax2 + sin x)
= q sin x (ax2 + sin x) + (p + q cos x) (2ax + cos x)
Kindly consider the following
69.
69. Given, f (x) =
So,
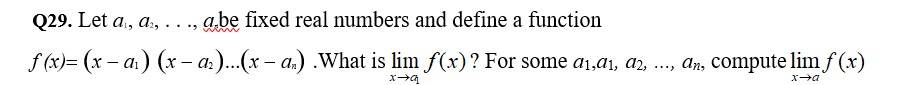
29.
Given, f (x) = (x-a1) (x-a2)… (x-an)
So,
= (a1-a1) (a1-a2) … (a1-an)
= 0 (a1-a2) … (a1-an)
= 0
And
= (a-a1) (a-a2) … (a-an)
Explore exams which ask questions on Maths Ncert Solutions class 11th
Select your preferred stream
Maths Ncert Solutions class 11th Exam
Student Forum
Other Similar chapters for you
- Binomial Theorem
- Probability
- Statistics
- Mathematical Reasoning
- Limits and Derivatives
- Introduction to Three Dimensional Geometry
- Conic Sections
- Straight Lines
- Sequences and Series
- NCERT Maths 11th
- Permutations and Combinations
- Linear Inequalities
- Complex Numbers and Quadratic Equations
- Principle of Mathematical Induction
- Trigonometric Functions
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test