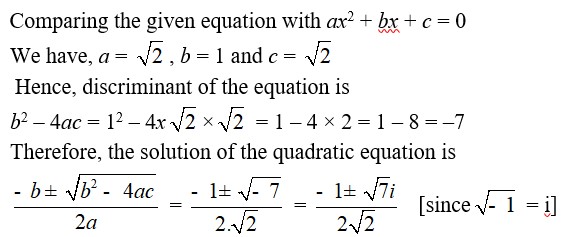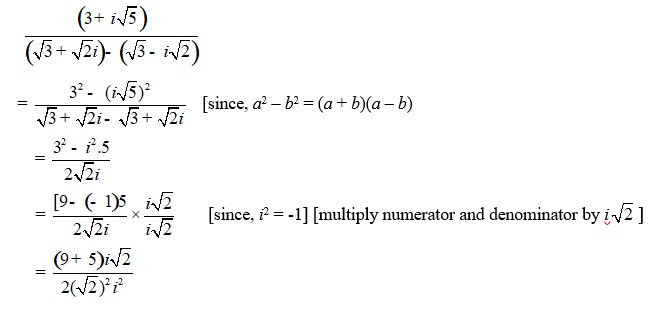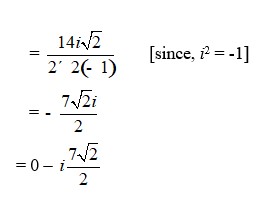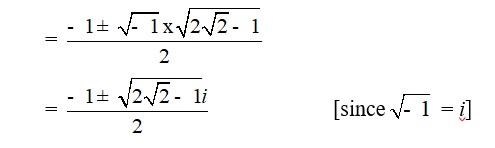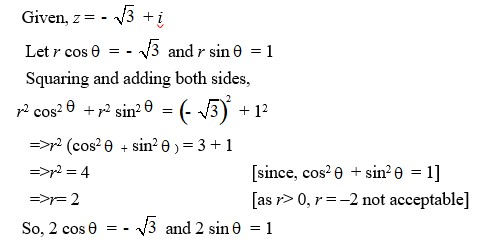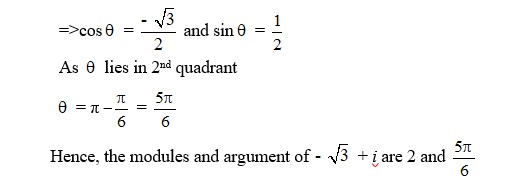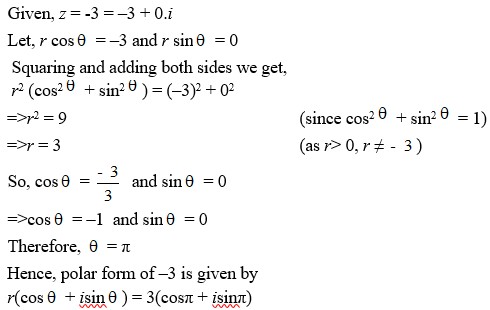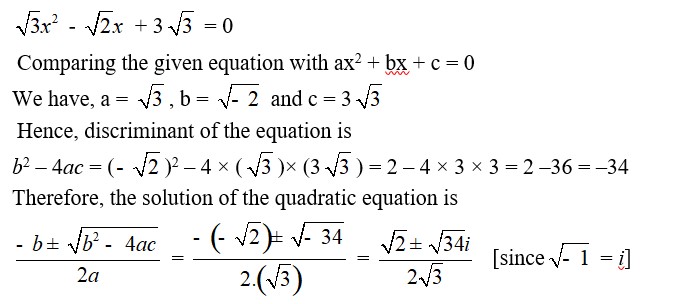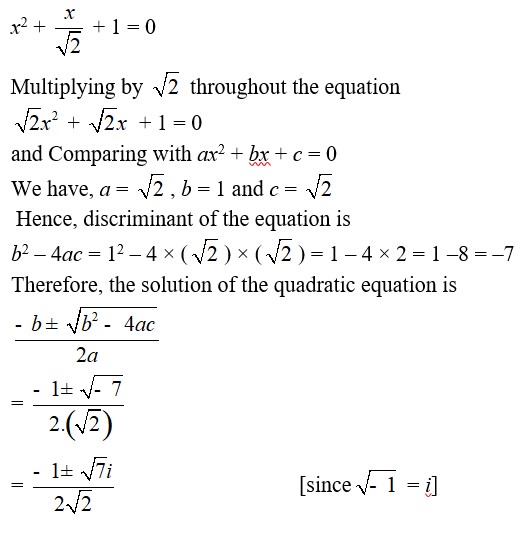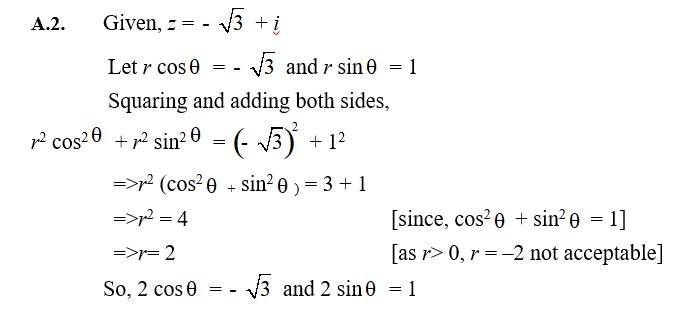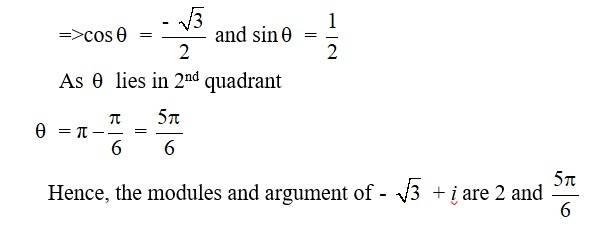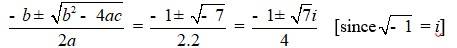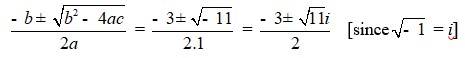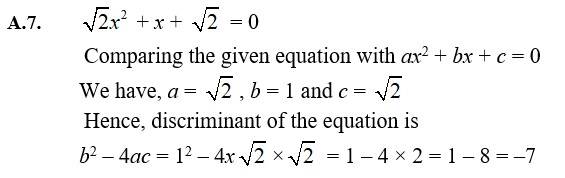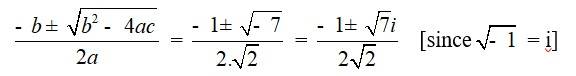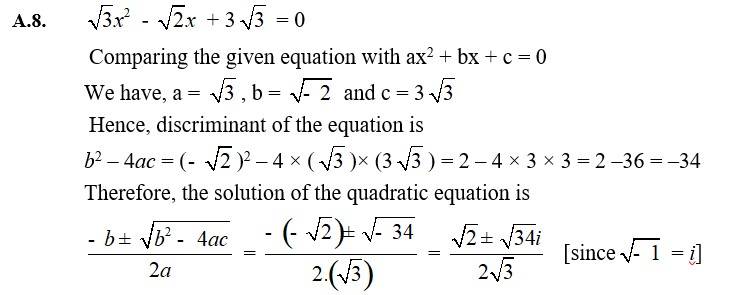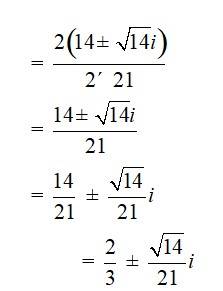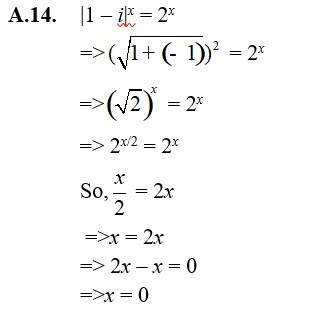Complex Numbers Class 11 Solutions cover concepts beyond real numbers. The chapter explores complex numbers, their calculations, and the algebra of quadratic equations. In many scenarios, we need to extend the real number system to a larger system to find solutions. Complex Numbers Class 11 NCERT Solutions are designed by the subject matter experts at Shiksha. Class 11 students can find a reliable NCERT solution here in a step-by-step explanation. It will help them to understand how to solve the questions based on the Complex Numbers Class 11.
To get access to the quick revision notes of Chemistry, Physics, and Maths, explore the NCERT Class 11 Notes here.
- Overview of Complex Numbers Class 11 Solutions
- Class 11 Math Complex Number & Quadratic Equations: Key Topics, Weightage
- Important Formulas of Complex Numbers Class 11
- Download Class 11 Maths Chapter 4 NCERT Solutions PDF for Free
- Class 11 Complex Numbers and Quadratic Equations Exercise 5.1 Solutions
- Class 11 Complex Numbers and Quadratic Equations Exercise 5.2 Solutions (Old NCERT)
- Class 11 Complex Numbers and Quadratic Equations Exercise 5.3 Solutions (Old NCERT)
- Class 11 Complex Numbers and Quadratic Equations Miscellaneous Exercise Solutions
Overview of Complex Numbers Class 11 Solutions
Let's have a snapshot of the NCERT Solutions Complex Numbers Class 11:
- A complex number is in the form of a+ib, where a and b are real numbers. The a is the real part, and b is the imaginary part.
- If z1 = a+ib and z2 = c+id, Then,
- There exists a complex number for any non-zero complex number - .
- For any integer k, To access the comprehensive NCERT notes of Class 11 and Class 12 of Chemistry, Physics, Maths, students must check here - NCERT Solutions Class 11 and 12.
Class 11 Math Complex Number & Quadratic Equations: Key Topics, Weightage
While preparing for any new chapter, it is important to know the topics in advance. See below the topics covered in the Complex Numbers Class 11:
| Exercise | Topics Covered |
|---|---|
| 4.1 | Introduction |
| 4.2 | Complex Numbers |
| 4.3 | Algebra of Complex Numbers |
| 4.4 | The Modulus and the Conjugate of a Complex Number |
| 4.5 | Argand Plane and Polar Representation |
Complex Numbers Class 11 Weightage In JEE Mains
| Exam | Number of Questions | Weightage |
|---|---|---|
| JEE Mains | 1-2 questions | 3.3% to 6.6% |
Related Links
| Class 11 Maths NCERT Notes | NCERT Notes for Class 11 & 12 | NCERT Solutions for Class 11 Maths |
Important Formulas of Complex Numbers Class 11
Important Formulae of Chapter 4 Class 11 Maths for CBSE and Competitive Exams
-
Complex Number Representation:
- (where is the real part, is the imaginary part)
- (Conjugate of )
- (Modulus of )
-
Polar Form of a Complex Number:
- where and
-
De Moivre’s Theorem:
-
-
Quadratic Equation Formula:
- Roots of
- Roots of
- Discriminant (D):
- If Two distinct real roots.
- If Two equal real roots.
- If
Two complex conjugate roots:
Check out dropped topics from Chapter 4 Complex Numbers and Quadratic Equations : Polar representation of complex numbers. Statement of the Fundamental Theorem of Algebra, solution of quadratic equations (with real coefficients) in the complex number system, and the square root of a complex number.
Download Class 11 Maths Chapter 4 NCERT Solutions PDF for Free
The students can download the free complex numbers PDF from the link below. The solutions are ideal for the school exam preparation, CBSE Board and competitive exam preparation such as JEE Main.
Chapter 5 Complex Numbers and Quadratic Equations Class 11 NCERT Solutions: Free PDF Download
Class 11 Complex Numbers and Quadratic Equations Exercise 5.1 Solutions
Class 11 Maths ch 5 Ex 4.1 is important to help students understand fundamental principles of complex numbers. Complex Number Exercise 4.1 includes problems related to the definition of Complex numbers, their algebraic representation, and basic operations like addition, subtraction, multiplication, and division. Students also learn about the concept of real and imaginary numbers and their representation on the number line. NCERT Solution of Ch 5 Class 11 Exercise 4.1 is available below;
Class 11 Ch 5 Complex Numbers Exercise 4.1 SolutionsExpress each of the complex number given in the Exercises 1 to 10 in the form a + ib. Q1. (5i) |
| A.1.(5i) = 5 ×i2 [since i2 = –1] = –3 (–1) = 3 So, (5i) = 3 + i0 |
| Q2. i9 + i19 |
| A.2. i9 + i19 = i4x2+1 + i4x4+3 [Since, i4k+1 = i and i4k+3 = – i] = i – i = 0 So, i9 + i19 = 0 + i0 |
| Q3. i– 39 |
| A.3. i– 39 = = = [Since, i4k+3 = –i] = × [multiplying numerator and denominator by i] = = [since, i2 = –1] = i So, i –39 = 0 + i |
| Q4. 3(7 + i7) + i(7 + i7) |
| A.4. 3(7 + i7) + i(7 + i7) = 21 + 21i + 7i + 7i2 = 21 + 28i + 7(–1)[since i2 = –1] = 21 + 28i – 7 = 14 + 28i |
| Q5. (1 – i) – ( –1 + i6) |
| A.5. (1 – i) – (–1 + i6) = 1 – i + 1 – i6 = 2 – 7i |
| Q6. – |
| A.6. – = + – 4 – = – 4 + i = + i = + i = – i |
| Q7. |
| A.7. = + + 4 + + – i = = + = + |
| Q8. (1 – i)4 |
| A.8. (1 – i)4 = [(1 – i)2]2 = [1 + i2 – 2.i]2 [since, (a - b)2 = a2 + b2 – 2ab] = [1 – 1 – 2i]2 [since, i2 = – 1] = (–2i)2 = 4i2 = – 4 = – 4 + 0i |
| Q9. |
| A.9. = [since, (a + b)3 = a3 + b3 + 3ab(a + b)] = [since, i3 = i2.i = –i and i2 = –1] = + 27(–i) + + (3i× 3i) = – 27i + i – 9 = + i(–27 + 1) = – i26 |
| Q10. |
| A.10. = = = [since, (a + b)3 = a3 + b3 + 3ab(a + b)] = (–1) [since, i3 = i2.i = –i and i2 = –1] = (–1) = (–1) = |
| Find the multiplicative inverse of each of the complex numbers given in the Exercises 11 to 13. Q11. 4 – 3i |
| A.11. Let Z = 4 – 3i Then = 4 + 3i And, z|2 = 42+(-3)2= 16 + 9 = 25 Hence, z-1 = = = + |
| Q12. √5 + 3i |
| A.12. Let z = √5 + 3i Then, = √5 - 3i And, |z|2 = ( √5 )2 + (3)2 = 5 + 9 = 14 So, multiplicative inverse of √5 + 3i is given by
|
| Q13. –i |
| A.13. Let z = -i Then = i And |z|2 = (-1)2 = 1 So, multiplicative inverse of –i is given by z-1 = = = i = 0 + i1 |
| Q14. Express the following expression in the form of a + ib: |
Commonly asked questions
Class 11 Maths Ch 5 Exercise 5.2 Solutions
Find the modulus and the arguments of each of the complex numbers in Exercises 1 to 2.
15. z = –1 - i √3
15. Kindly go through the solution
41. If (a + ib) (c + id) (e + if) (g + ih) = A + iB, then show that(a2+ b2) (c2+ d2) (e2+ f2) (g2+ h2) = A2+ B2
41. Given,
(a + ib) (c + id) (e + if) (g + ih) = A + iB
We know that,
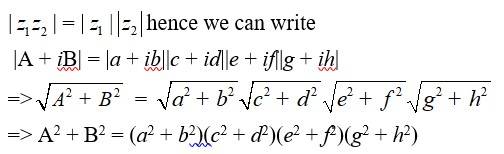
Hence proved.
34. If z1 = 2 – i, z2 = 1 + i, find
34. z1 = 2 – i ,z2 = 1 + i
=
=
=
=
= × [multiply numerator and denominator by (1 + i)]
=
= [since, i2 = –1]
=
=
= |1 + i|
4. 3(7 + i7) + i(7 + i7)
4. 3 (7 + i7) + I (7 + i7)
= 21 + 21i + 7i + 7i2
= 21 + 28i + 7 (–1) [since i2 = –1]
= 21 + 28i – 7
= 14 + 28i
29. Reduce to the standard form.
29.
=
=
=
=
=
= .. [since, i2 = –1]
=
= × [multiplying denominator and numerator by 28 + 10i]
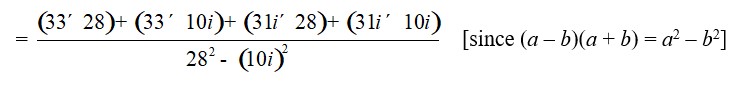
=
= [since, i2 = –1]
=
=
=
= +
24. √2x² + x + √2 = 0
24. Kindly go through the solution
Class 11 Ch 5 Complex Numbers Exercise 4.1 Solutions
Express each of the complex number given in the Exercises 1 to 10 in the form a + ib.
1. (5i)
1. (5i)
= 5 ×i2 [since i2 = –1]
= –3 (–1)
= 3
So, (5i) = 3 + i0
Find the multiplicative inverse of each of the complex numbers given in the Exercises 11 to 13.
11. 4 – 3i
11. Let Z = 4 – 3i
Then = 4 + 3i
And, z|2 = 42+ (-3)2= 16 + 9 = 25
Hence, z-1 = = = +
10.
10.
=
=
= [since, (a + b)3 = a3 + b3 + 3ab(a + b)]
= (–1) [since, i3 = i2.i = –i and i2 = –1]
= (–1)
= (–1)
=
Class 11 Complex Numbers Ex 5.3 Solutions
18. x2+ 3 = 0
18. x2 + 3 = 0
=>x2 = –3
=>x =
=>x= ± √3 [since, √-1 = i]
=>x = 0 ± √3
38. Find the modulus of
38. –
=
= [Since, (a + b)2 = a2 + b2 + 2ab
(a – b)2 = a2 + b2 – 2ab
a2 – b2 = (a + b) (a – b)]
= [Since, i2 = –1]
=
= 2i

39. If (x + iy)3 = u + iv, then show that .
39. (x + iy)3 = u + iv
=>x3 + (iy)3 + 3.x.iy (x + iy) = u + iv [since, (a + b)3 = a3 + b3 + 3ab (a + b)]
=>x3 – iy3 + 3x2yi + 3xy2i2 = u + iv
=>x3 – iy3 + 3x2yi – 3xy2 = u + iv [since, i2 = -1]
=> (x3 – 3xy2) + i (3x2y – y3) = u + iv
Equating real and imaginary part we get,
u = x3 – 3xy2 and v = 3x2y – y3
Now, +
= +
= +
= x2 – 3y2 + 3x2 – y2
= 4x2 – 4y2
= 4 (x2 – y2)
Hence proved.
14. Express the following expression in the form of a + ib:
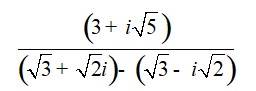
14. Kindly go through the solution
12. √5 + 3i
12. Let z = -i
Then = i
And |z|2 = (-1)2 = 1
So, multiplicative inverse of –i is given by
z-1 = = = I = 0 + i1

26. Kindly Consider the following
![]()
26. Kindly go through the solution
16. z = -√3 + i
16. Kindly go through the solution
5. (1 – i) – ( –1 + i6)
5. (1 – i) – (–1 + i6)
= 1 – I + 1 – i6
= 2 – 7i
6. –
6. –
= + – 4 –
= – 4 + i
= + i
= + i
= – i
28. For any two complex numbers z1 and z2, prove that Re (z1 z2) = Re z1 Re z2 – Imz1 Imz2
28. To proof, Re (z1z2) = Re z1 Re z2 – Imz1 Imz2
Let z1 = x1 + iy1 and z2 = x2 + iy2 be two complex number.
Then, z1.z2 = (x1 + iy1) (x2 + iy2)
=x1x2 + ix1y2 + ix2y1 + i2y1y2
= x1x2 + ix1y2 + ix2y1 – y1y2 [since, i2 = -1]
= (x1x2 – y1y2) + i (x1y2 + x2y1)
As, Re (z1z2) = (x1) (x2) – (y1) (y2)
Now, RHS = Re z1 Re z2 – Imz1Imz2 = x1x2 – y1y2
Therefore, Re (z1z2) = Rez1Rez2 – Imz1Imz2
Hence proved.
36. Let z1 = 2 – i, z2 = –2 + i. Find (i) (ii)
36. Z1 = 2 – i, z2 = –2 + i
Z1z2 = (2 – i)(–2 + i)
= –4 + 2i + 2i – i2
= –4 + 4i + 1[since, i2 = –1]
= –3 + 4i
= 2 + i
i. =
= × [multiply denominator and numerator by (2 – i)]
=
= [since, i2 = –1]
=
=
= +
So, Re( ) =
ii. =
=
= [since, i2 = –1]
= + 0i
Therefore, Im = 0
Convert the complex number given in Exercise 3 in the polar form:
17. –3
17. Kindly go through the solution
20. x2 + 3x + 9 = 0
20. x2 + 3x + 9 = 0
Comparing the given equation with ax2 + bx + c = 0
We have, a = 1, b = 3 and c = 9
Hence, discriminant of the equation is
b2 – 4ac = 32 – 4 * 1* 9 = 9 – 36 = –27
Therefore, the solution of the quadratic equation is
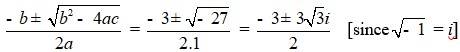
40. Find the number of non-zero integral solutions of the equation![]()
40.
So, the only solution of the given equation is 0.
Hence, there is no non – zero integral solution of the given equation.
21. –x2 + x – 2 = 0
21. –x2 + x – 2 = 0
Comparing the given equation with ax2 + bx + c = 0
We have, a = –1, b = 1 and c = –2
Hence, discriminant of the equation is
b2 – 4ac = 12 – 4 * (-1)* (-2) = 1 – 8 = –7
Therefore, the solution of the quadratic equation is

7.
7.
= + + 4 + + – i
=
= +
= +
Solve each of the equation in Exercises 30 to 33.
30. ![]()
Multiplying the above equation by 3, we get
9x2 + 12x + 20 = 0
and Comparing with ax2 + bx + c = 0
We have, a =9, b = –12 and c = 20
Hence, discriminant of the equation is
b2 – 4ac = (–12)2 – 4 * 9* 20 = 144 – 720 = –576
Therefore, the solution of the quadratic equation is
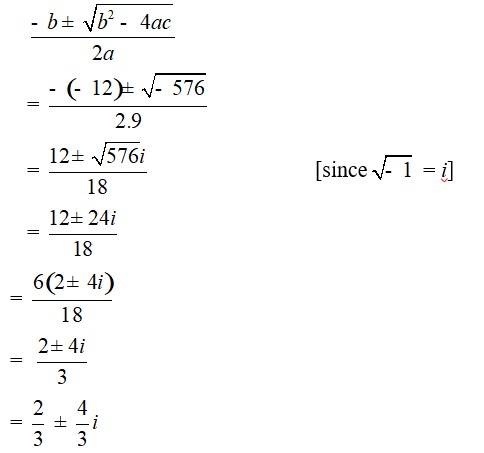
37. Find the real numbers x and y if (x – iy) (3 + 5i) is the conjugate of –6 – 24i.
37. Let z = (x – iy) (3 + 5i)
= 3x + 5xi – 3yi – 5yi2
= (3x + 5y) + (5x – 3y)i
Given, = –6 – 24i
=> (3x + 5y) – (5x – 3y)i = –6 – 24i
Equating real and imaginary part,
3x + 5y = –6 - (1)
5x – 3y = 24 - (2)
Multiplying (1) by 3 and (2) by 5 and adding them, we get
9x + 15y + 25x – 15y = –18 + 120
=> 34x = 102
=>x = 102/34 = 3
Putting x = 3 in (1) we get,
3 × 3 + 5y = –6
=> 9 + 5y = –6
=> 5y = –6 – 9
=> 5y = –15
=>y = –15/5 = –3
Hence, the values of x and y are 3 and –3 respectively.
42. If , then find the least positive integral value of m.
42. We have,
= 1
=> = 1 [multiply denominator and numerator of LHS by (1 + i)]
=> = 1 [since, (a – b) (a + b) = a2 – b2]
=> = 1 [since, i2 = –1]
=> = 1
=>im = 1
=>im = i4k [since, i4k = 1]
So, m = 4k where k = integer
Therefore, least positive integral value of m is,
m = 4 × 1
m = 4
23. x2 – x + 2 = 0
23. x2 – x + 2 = 0
Comparing the given equation with ax2 + bx + c = 0
We have, a = 1, b = –1 andc = 2
Hence, discriminant of the equation is
b2 – 4ac = (-1)2 – 4 * 1 * 2 = 1 – 8 = –7
Therefore, the solution of the quadratic equation is
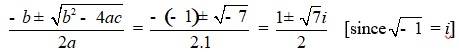
25. √3x² - √2x + 3√3 = 0
25. Kindly go through the solution
27. Kindly Consider the following
![]()
27. Kindly go through the solution
31. Kindly Consider the following
![]()
31. ![]()
Multiplying the above equation by 2, we get
2x2 - 4x + 3 = 0
and Comparing with ax2 + bx + c = 0
We have, a = 2, b = –4 and c = 3
Hence, discriminant of the equation is
b2 – 4ac = (-4)2 – 4 * 2* 3 = 16 – 24 = –8
Therefore, the solution of the quadratic equation is
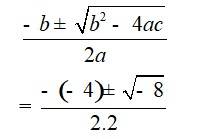
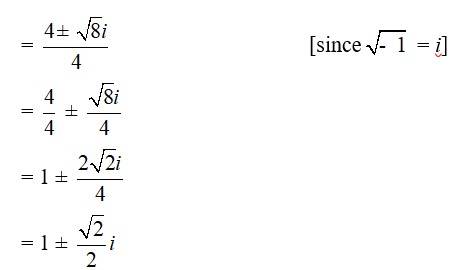
32. 27x2 – 10x + 1 = 0
32. 27x2 – 10x + 1 = 0
Comparing the given equation with ax2 + bx + c = 0
We have, a = 27, b = –10 andc = 1
Hence, discriminant of the equation is
b2 – 4ac = ( 10)2 – 4 * 27 * 1 = 100 – 108 = –8
Therefore, the solution of the quadratic equation is
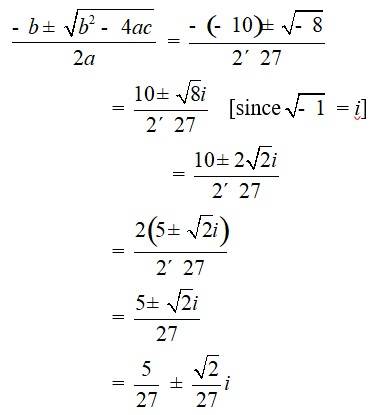
33. 21x2 – 28x + 10 = 0
33. 21x2 – 28x + 10 = 0
Comparing the given equation with ax2 + bx + c = 0
We have, a = 21, b = –28 andc = 10
Hence, discriminant of the equation is
b2 – 4ac = ( 28)2 – 4 * 21 * 10 = 784 – 840 = –56
Therefore, the solution of the quadratic equation is
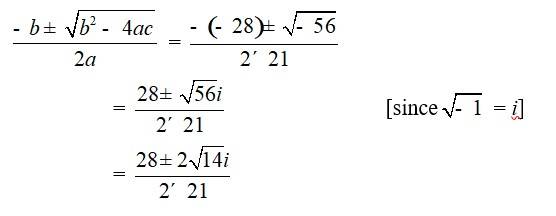
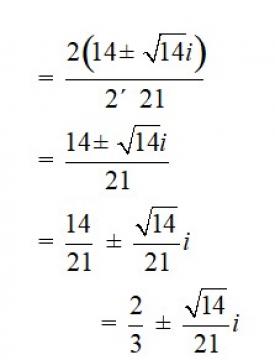
35. If a + ib , prove that a2 + b2
35. Let, z = a + ib
=
= [since, (a + b)2 = a2 + b2 + 2ab]
= [since, i2 = –1]
= +
So, |z|2 = a2 + b2
= +
= [since, (a + b)2 = a2 + b2 + 2ab]
=
=
= [as, (a + b)2 = a2 + b2 + 2ab]
Hence proved.
Class 11 Complex Numbers and Quadratic Equations Exercise 5.2 Solutions (Old NCERT)
Ch 5 Maths Class 11 exercise 5.2 focus on more operations and properties related to Complex number algebra. This exercise focuses on algebraic representation and various operations like addition, subtraction, multiplication, and division of complex numbers. Exercise 5.2 also discusses more specific topics such as the modulus and conjugate of a complex number. Students can check the Solution of Ch 5 Ex 5.2 below;
Class 11 Maths Ch 5 Exercise 5.2 SolutionsFind the modulus and the arguments of each of the complex numbers in Exercises 1 to 2. Q1. z = –1 - i √3 |

|
| Q2. z = -√3 + i |
| Convert the complex number given in Exercise 3 in the polar form: Q3. –3 |
Class 11 Complex Numbers and Quadratic Equations Exercise 5.3 Solutions (Old NCERT)
Ex 5.3 Ch 5 class 11 Maths focuses on introducing more advanced topics such as complex numbers on a graph representation( Argand plane). Class 11 Exercise 5.3 NCERT Solutions discusses in detail concepts like the size (modulus) and angle (argument) of a complex number. This exercise also includes problems related to the polar form of complex numbers, which is useful for solving advanced math problems. Exercise 5.3 contains 10 short answer-type questions. Students can check the NCERT Solution below;
Class 11 Complex Numbers Ex 5.3 SolutionsQ1. x2+ 3 = 0 |
| A.1. x2 + 3 = 0 =>x2 = –3 =>x = =>x= ± √3 [since, √-1 = i] =>x = 0 ± √3 |
| Q2. 2x2 + x + 1 = 0 |
| A.2. 2x2 + x + 1 = 0 Comparing the given equation with ax2 + bx + c = 0, a = 2, b = 1 and c = 1 Hence, the discriminant of the equation is b2 – 4ac = 12 – 4 ×2×1 = 1 – 8 = –7 Therefore, the solution of the quadratic equation is
|
| Q3. x2 + 3x + 9 = 0 |
| A.3. x2 + 3x + 9 = 0 Comparing the given equation with ax2 + bx + c = 0 We have, a = 1, b = 3 and c = 9 Hence, discriminant of the equation is b2 – 4ac = 32 – 4 × 1× 9 = 9 – 36 = –27 Therefore, the solution of the quadratic equation is
|
| Q4. –x2 + x – 2 = 0 |
| A.4. –x2 + x – 2 = 0 Comparing the given equation with ax2 + bx + c = 0 We have, a = –1, b = 1 and c = –2 Hence, discriminant of the equation is b2 – 4ac = 12 – 4 ×(-1)×(-2) = 1 – 8 = –7 Therefore, the solution of the quadratic equation is
|
| Q5. x2 + 3x + 5 = 0 |
| A.5. x2 + 3x + 5 = 0 Comparing the given equation with ax2 + bx + c = 0 We have, a = 1, b = 3 and c = 5 Hence, discriminant of the equation is b2 – 4ac = 32 – 4 × 1 × 5 = 9 – 20 = –11 Therefore, the solution of the quadratic equation is
|
| Q6. x2 – x + 2 = 0 |
| A.6. x2 – x + 2 = 0 Comparing the given equation with ax2 + bx + c = 0 We have, a = 1, b = –1 andc = 2 Hence, discriminant of the equation is b2 – 4ac = (-1)2 – 4 × 1 × 2 = 1 – 8 = –7 Therefore, the solution of the quadratic equation is
|
| Q7. √2x² + x + √2 = 0 |
| Q8. √3x² - √2x + 3√3 = 0 |
| Q9. |
| Q10. |
Class 11 Complex Numbers and Quadratic Equations Miscellaneous Exercise Solutions
Explore exams which ask questions on Maths Ncert Solutions class 11th
Select your preferred stream
Maths Ncert Solutions class 11th Exam
Student Forum
Other Similar chapters for you
- Statistics
- Mathematical Reasoning
- Limits and Derivatives
- Introduction to Three Dimensional Geometry
- Conic Sections
- Straight Lines
- Sequences and Series
- NCERT Maths 11th
- Permutations and Combinations
- Linear Inequalities
- Complex Numbers and Quadratic Equations
- Principle of Mathematical Induction
- Trigonometric Functions
- Relations and Functions
- Sets
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test