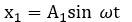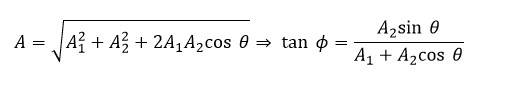Simple Harmonic Motion (SHM) occurs when an object oscillates, and the force pulling it back to its starting position is directly proportional to the distance it has moved from that position. When reading about oscillations in Class 11 Physics, you know that a body, when it repeats its motion along a definite path and does so at regular time intervals, is said to exhibit periodic motion. The time interval is often referred to as the harmonic motion period (T). This path of periodic motion can be linear, circular, elliptical, or another other curve.
SHM is special because it has a unique characteristic: the restoring force that pulls the object back toward its equilibrium position is directly proportional to how far the object has moved from that position. This proportional relationship between force and displacement is what distinguishes simple harmonic motion from other types of periodic motion. We uncover about Simple Harmonic Motion more today.
- What is Simple Harmonic Motion?
- NCERT Definition of Simple Harmonic Motion
- Working Principle of Simple Harmonic Motion
- Types of SHM
- Simple Harmonic Motion (SHM) Equation
- Characteristics of SHM
- Graph of Speed (v) vs Displacement (x) in Simple Harmonic Motion
- SHM as a Projection of Uniform Circular Motion
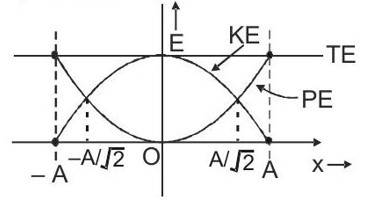
- Energy of SHM
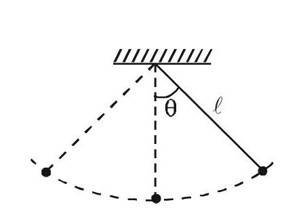
- Simple Pendulum and SHM
- Compound Pendulum / Physical Pendulum and SHM
- Torsional Pendulum and SHM
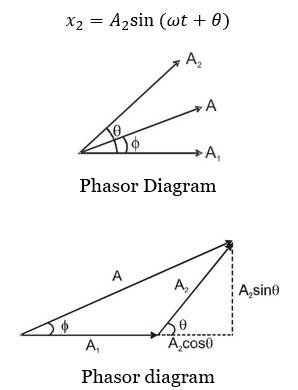
- Superposition of Two Simple Harmonic Motions
- Revision Notes for Physics Class 11
- NCERT Solutions Physics Class 11
What is Simple Harmonic Motion?
Simple Harmonic Motion (SHM) represents a specific form of repetitive motion in which an object moves to and from a central rest position. This motion is termed "simple" due to its mathematical description using basic trigonometric functions such as sine or cosine waves.
Importance of Learning Simple Harmonic Motion for Exams
- SHM frequently appears in JEE Main and Advanced exams, with at least one question expected annually. Problems typically focus on finding time period, frequency, amplitude, phase, velocity, acceleration, and energy for systems like springs and pendulums. These variables are also part of your later chapter on Waves, especially when you are learning about displacement relation of progressive waves.
- If you can master SHM concepts and problem patterns that we show here, you can easily score full marks, as most questions involve direct formula application or basic analysis.
Practice exercises for NCERT Solutions for Chapter 13 free!
NCERT Definition of Simple Harmonic Motion
The NCERT textbook defines Simple Harmonic Motion as -
"Consider a particle oscillating back and forth about the origin of an x-axis between the limits +A and –A ... This oscillatory motion is said to be simple harmonic if the
displacement x of the particle from the origin varies with time as : x (t) = A cos (ω t + φ)".
Key points to remember about Simple Harmonic Motion
- Repetitive motion between fixed boundaries
- Displacement varies sinusoidally with time
- Motion is described by three constants (A, ω, φ) that define its amplitude, frequency, and phase
Working Principle of Simple Harmonic Motion
SHM operates on the fundamental principle of restoring force.
When an object is displaced from its equilibrium position, a force acts to pull it back toward that central position. This restoring force is directly proportional to the displacement and always points toward equilibrium.
Key Operating Mechanisms:
- The driving mechanism that maintains oscillation by constantly pulling the object back to its rest position
- In ideal SHM, mechanical energy remains constant as it continuously converts between kinetic energy (at equilibrium) and potential energy (at extreme positions)
- The proportional restoring force creates regular, repeating motion with fixed time intervals
Types of SHM
We need to learn about two major types of simple harmonic motion.
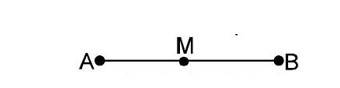
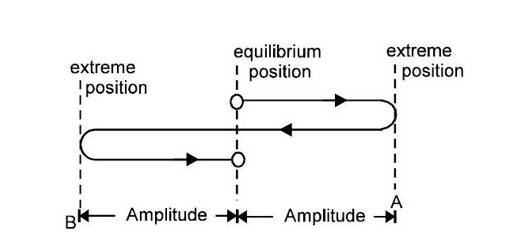
- Linear SHM: When a moving body or particle undergoes to and fro motion along a straight line in equilibrium position. A and B are two extreme ends. M is the mean position. and are extreme positions. is the mean position.
Simple Harmonic Motion (SHM) Equation
For SHM to work, the main condition is
F
Where,
positive constant for an SHM = Force constant
displacement from the mean position.
or
[differential equation of SHM]
where
Its solution is
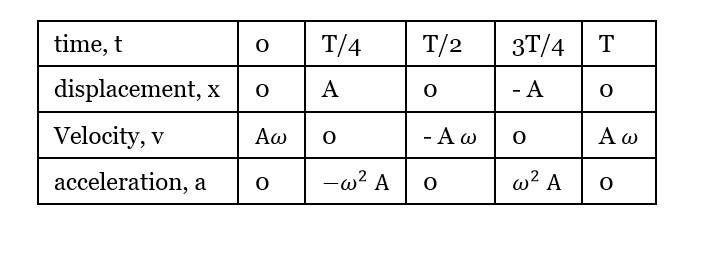
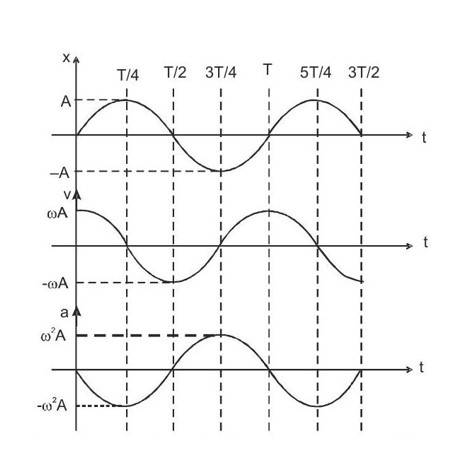
Characteristics of SHM
Let's look at the characteristics of Simple Harmonic Motion.
Note: In the figure shown, the path of the particle is on a straight line.
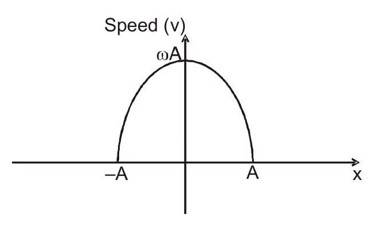
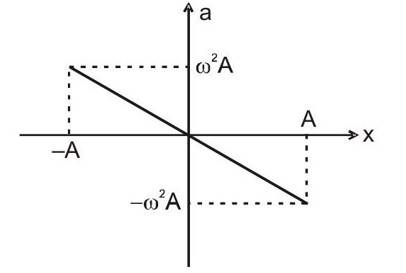
Graph of Speed (v) vs Displacement (x) in Simple Harmonic Motion
Let's look at two graphical ways to represent Simple Harmonic Motion.
When the Graph is Elliptical
The velocity equation in simple harmonic motion is
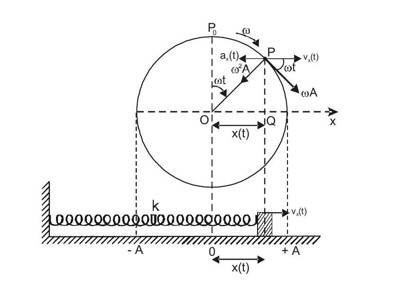
SHM as a Projection of Uniform Circular Motion
Energy of SHM
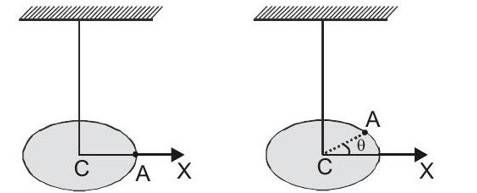
Simple Pendulum and SHM
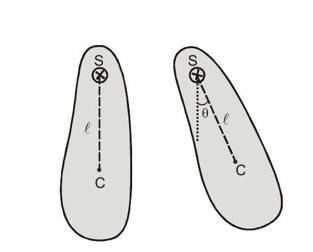
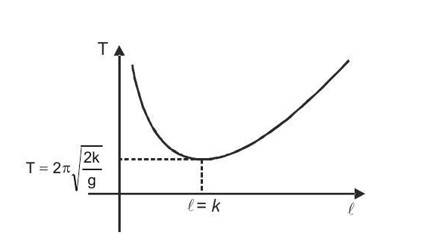
Compound Pendulum / Physical Pendulum and SHM
Torsional Pendulum and SHM
Superposition of Two Simple Harmonic Motions
Revision Notes for Physics Class 11
NCERT Solutions Physics Class 11
Commonly asked questions
What is the restoring force in Simple Harmonic Motion?
The restoring force in SHM is the force that always acts towards the mean position and is directly proportional to the displacement from it. It follows F=? kx. Here, the negative sign indicates the force is in the opposite direction to the displacement.
What is meant by the phase of SHM?
The phase in SHM tells us the position and direction of motion of the particle at a specific instant. It determines the state of oscillation and includes both displacement and time information.
What is resonance in forced oscillations?
Resonance occurs when the frequency of an external periodic force matches the natural frequency of a system. From that, physicists know that resonance causes the amplitude of oscillations to increase significantly. This can be beneficial in devices, such as musical instruments, but dangerous in structures like bridges.
Physics Oscillations Exam
Student Forum
Other Topics under this Chapter
Other Class 11th Physics Chapters
- Physics Mechanical Properties of Solids
- NCERT Class 11 Physics
- NCERT Class 11 Notes
- NCERT Notes
- Physics Motion in Plane
- Physics Mechanical Properties of Fluids
- Physics Motion in Straight Line
- Physics System of Particles and Rotational Motion
- Physics Oscillations
- Physics Waves
- Physics Thermal Properties of Matter
- Physics Motion
- Physics Gravitation
- Physics Thermodynamics
- Physics Work, Energy and Power
- Physics Units and Measurement
- Physics Laws of Motion

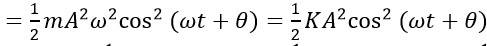 (
(
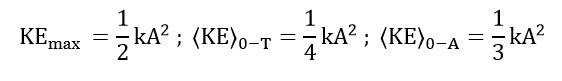

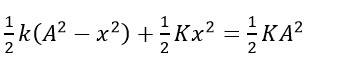
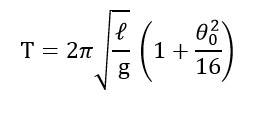
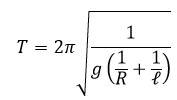 Where, R = Radius of the Earth
Where, R = Radius of the Earth
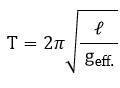
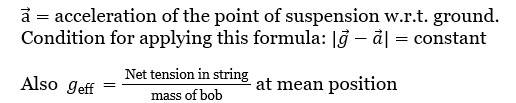
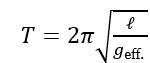
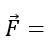
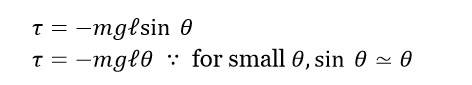
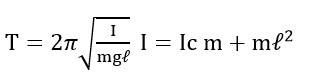
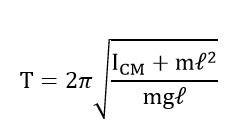

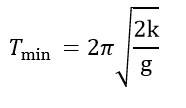
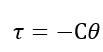
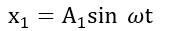
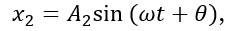
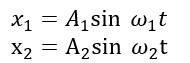
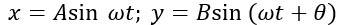
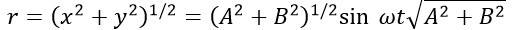 ,
,