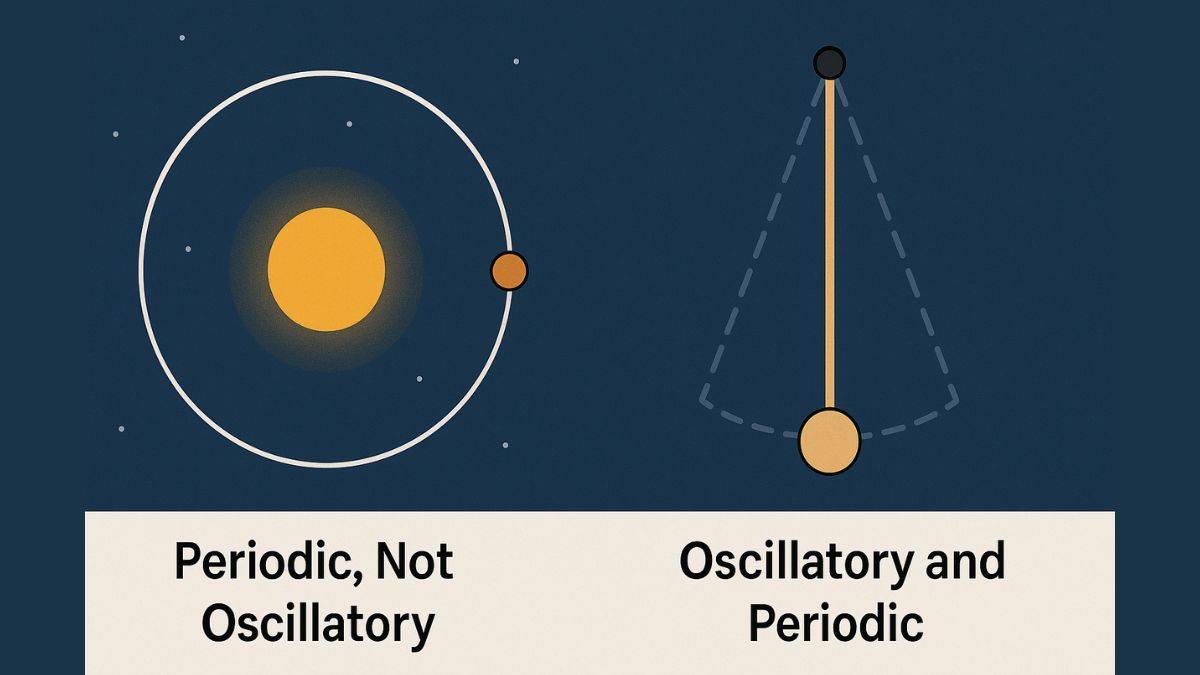
The Earth orbits the sun 365 days a year. It repeats periodically. If such a motion repeats itself at fixed time intervals, we call it a periodic motion. Oscillatory motion is a special case of periodic motion you see in a pendulum or metronome. The object moves back and forth about a central point.
All you should know is that some types of periodic motions are not oscillatory, but all oscillatory motion is periodic. In physics, we have various parameters that enable us to differentiate and calculate periodic and oscillatory motions. Some major ones are Period, Frequency, and Displacement, especially when practising the NCERT Solutions on Oscillations. We cover all of these below.
- What is Periodic Motion?
- What is Oscillatory Motion?
- Periodic vs. Oscillatory Motion: The Key Differences
- Measuring Periodic Motion: Key Parameters
- Mathematics of Oscillation: Displacement Equation in SHM and Periodic Functions
- Periodic and Oscillatory Motions for JEE 2026 Preparation
- Revision Notes for Physics Class 11
- NCERT Solutions for Physics Class 11
What is Periodic Motion?
Periodic motion describes any movement that repeats over a time period that is always fixed.
NCERT says, “a motion that repeats itself at regular intervals of time is called periodic motion.”
If you can predict an object's movement that will return to the same position and move in the same direction after a specific time, that motion is periodic.
Key Characteristics of Periodic Motion
These are necessary conditions for a movement to be considered as a periodic motion.
- Periodic Motion is Repetitive: The motion follows the same path repeatedly.
- Periodic Motion has a Fixed Time Interval: Each repetition takes the same amount of time (the Period).
Examples of Periodic Motion
- The hands of a clock rotating is an example of repetitive motion. They repeat their paths at fixed time intervals.
- Earth’s rotation around its axis and the sun is another periodic motion example. The path is repetitive, and the movement occurs within the same time.
Go check Oscillations Class 11 Notes.
What is Oscillatory Motion?
Oscillatory motion is a special kind of periodic motion. A to-and-fro motion around a central or fixed point defines it. It’s also known as a vibration.
NCERT mentions, “If the body is given a small displacement from the position, a force comes into play which tries to bring the body back to the equilibrium point, giving rise to oscillations or vibrations.”
The force that NCERT mentions is known as the restoring force. This is the defining factor for understanding what oscillatory motion or vibration is. It’s because of the restoring force that the object pulls back to its equilibrium point.
Key Characteristics of Oscillatory Motion
Some essential conditions that make a periodic motion oscillatory.
- It always occurs about a stable equilibrium position.
- A restoring force must always act to pull the object back to its equilibrium point.
Examples of Oscillatory Motion
- A string instrument vibrates/oscillates when struck. No matter how hard or soft you hit or strum the string, it gets back to its equilibrium position, as there is a restoring force that works here.
- A simple pendulum is an important example of oscillatory motion. It connects with larger concepts such as SHM, which works through restoring force and gravity to come back to its equilibrium position.
Types of Oscillatory Motion
Another important aspect NCERT mentions is the types of oscillatory motion.
- Damped oscillations: In real life, oscillations slowly stop because of friction or other energy losses.
- Forced oscillations: A periodic outside force can keep something oscillating.
- Non-linear oscillations: Sometimes the restoring force isn’t perfectly proportional to displacement.
Periodic vs. Oscillatory Motion: The Key Differences
NCERT mentions, “Every oscillatory motion is periodic, but every periodic motion need not be oscillatory. Circular motion is a periodic motion, but it is not oscillatory.”
Knowing the difference between periodic and oscillatory motion is essential from a conceptual standpoint.
| Feature |
Periodic Motion |
Oscillatory Motion |
| Definition |
Repeats motion in regular time intervals. |
Moves back and forth about an equilibrium point. |
| Key Requirement |
A fixed time period. |
A fixed time period and a restoring force. |
| Nature |
Can be rotational, revolutionary, or vibrational. |
Is always a "to and fro" or vibrational motion. |
| Example |
Earth's orbit, a spinning fan. |
A swinging pendulum, a vibrating spring. |
| Relationship |
The broader category of repeating motion. |
A specific sub-type of periodic motion. |
Measuring Periodic Motion: Key Parameters
Here are some of the most essential parameters to consider when you are learning periodic and oscillatory motion in physics. Let's find out about the period and frequency relationship, along with others.
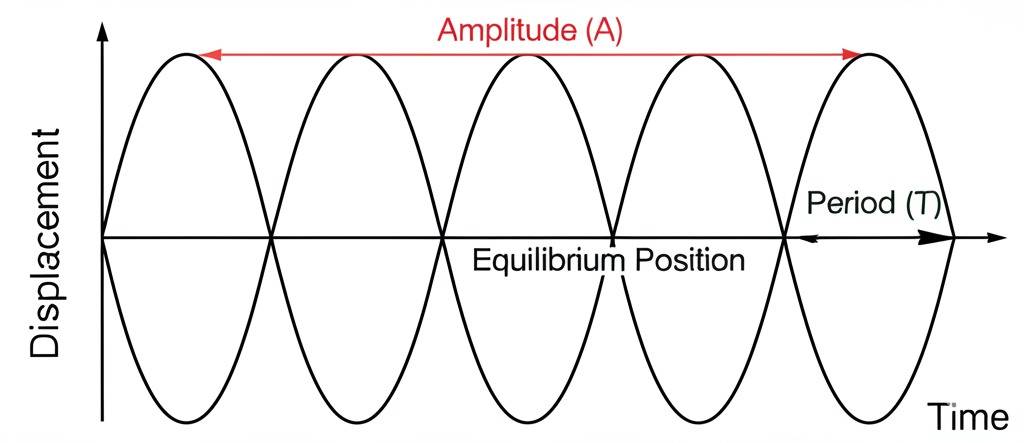
Period or Time Interval (T)
The Period is the smallest time interval the motion takes to complete one full cycle.
Symbol of Period: T
SI Unit of Period: seconds (s)
Period: Fast and Slow Motion Examples
Do remember that periodic motion cannot always have the same unit. For fast periodic motion, we use microseconds (μs). For slower, we could use days or years.
Fast Motion Example: AC current oscillates 50 times every second. The period is 0.02 seconds (20 milliseconds).
Slow Motion Example: The moon orbits around the Earth roughly every 27.3 days.
Frequency (ν or f)
Frequency indicates the number of complete cycles or oscillations that occur in one second. It is the inverse of the period.
Symbol of Frequency: ν (nu) or f
Formula for Frequency: ν = 1 / T
SI Unit for Frequency: Hertz (Hz), where 1 Hz = 1 cycle per second (s⁻¹).
Relationship Between Frequency and Period
If the period is long, the frequency is low. If the period is short, the frequency is high.
Displacement (x, y) and Amplitude (A)
Displacement in periodic and oscillatory motions refers to the position of the oscillating object at any given time. It’s measured from the equilibrium position.
Amplitude is the maximum possible displacement from that equilibrium position.
Mathematics of Oscillation: Displacement Equation in SHM and Periodic Functions
One of the most basic types of oscillations is Simple Harmonic Motion. NCERT mentions that this “motion arises when the force on the oscillating body is directly proportional to its displacement from the mean position.”
The Displacement Equation in SHM
The displacement x of an object in SHM at any time t can be described by a sinusoidal function.
x(t) = A cos(ωt + φ)
Let's break down this displacement equation.
- A (Amplitude): This is the maximum displacement from the centre.
- ω (Angular Frequency): It determines the rate at which oscillations occur. It's related to frequency ν by ω = 2πν. Its unit is radians per second.
- t (Time): This is the variable that represents time.
- (ωt + φ) (Phase): This is the argument of the cosine function. It determines the state of the oscillation at time t.
- φ (Phase Constant): This represents the initial phase at t = 0. It tells us where in the cycle the motion starts.
Understanding Periodic Functions in SHM
As you go through Functions in Maths, you find their application in understanding periodic functions in physics.
A periodic function is a mathematical function that repeats its values at regular time intervals. It should satisfy:
This means the value of the function repeats after every interval T.
In the case of SHM, both sine and cosine are periodic functions with a basic period of 2π radians.
In the equation, x(t) = A cos(ωt + φ)
- The cosine function repeats every time the angle, ωt + φ, increases by 2π. So if you add 2π, or 4π, or 6π to the angle. It's like going around the circle again.
- Since ω is the angular frequency (how fast the angle changes), the time to complete one full cycle (i.e., return to the same position) is: T = 2π / ω. This is how we calculate period from angular frequency.
Combining Waves and Fourier Analysis to Periodic Functions
Here’s another approach to understanding the periodic motion, especially when you move beyond a pure sine wave as that of Simple Harmonic Motion.
If you consider a complex periodic motion of an ocean tide. Had it been just the Moon’s gravity, the pattern of high and low tides would be simple periodic motion. But, in reality, ocean tides occur every 12 or 24 hours periodically, and the final ocean tide is the result of
- The primary gravitational pull from the Moon.
- A secondary gravitational pull from the Sun.
- The effects of the Earth's rotation.
- The complex shapes of coastlines and the ocean floor.
The tide at any given beach is the sum of all these effects. When the Sun and Moon are aligned (during a new or full moon), their gravitational pulls add up. That creates higher-than-average Spring Tides. When they are at right angles, their pulls partially cancel out, leading to lower-than-average Neap Tides.
So, to describe this complex periodic motion, we have to look into two concepts
- The superposition principle
- Fourier Theorem.
If you mix sine and cosine together, based on the superposition principle, you get
f(t) = A sin(ωt) + B cos(ωt)
Bringing along, what Fourier proved, any periodic function can be broken down into a sum of simple sine and cosine waves.
You can combine that mix into one neat sine wave like this period function.
f(t) = D sin(ωt + φ)
Where:
- D = √(A² + B²)
This is the total amplitude (how tall the wave is)
- φ = tan⁻¹(B/A)
This is the phase shift (where the wave starts)
So instead of juggling both sine and cosine, you just write it as one smooth wave with a new size and starting point.
Periodic and Oscillatory Motions for JEE 2026 Preparation
Expect numerical problems in JEE Main next year based on the displacement equation. The questions would test whether you can calculate the angular frequency or amplitude.
Based on the older question banks for JEE, it is essential to be clear about the connections among displacement, velocity, acceleration, and phase.
Periodic and oscillatory motions form the conceptual background for all these. Simply download JEE Main question papers for free, and start solving right away.
If you need more clarity on other topics, we have you covered with our Class 11 Physics Notes. Bookmark and read them anytime!
Revision Notes for Physics Class 11
Here are the notes for Physics Class 11. Revise the notes for each topic, in-depth.
| Units and Measurements Class 11 Notes | Mechanical Properties of Solids Class 11 Notes |
| Motion in a Straight Line Class 11 Notes | Mechanical Properties of Fluids Class 11 Notes |
| NCERT Class 11 Notes for Motion in a Plane | Thermal Properties of Matter Class 11 Notes |
| Laws of Motion Class 11 Notes | Thermodynamics Class 11 Notes |
| Work, Energy, and Power Class 11 Notes | Kinetic Theory of Gas Class 11 Notes |
| System of Particles and Rotational Motion Class 11 Notes | Oscillations Class 11 Notes |
| Gravitation Class 11 Notes | Waves Class 11 Notes |
Get an overview of Science Class 11.
| NCERT Class 11 Notes for PCM |
| NCERT Class 11 Physics Notes |
NCERT Solutions for Physics Class 11
Physics Oscillations Exam
Student Forum
Other Topics under this Chapter
Other Class 11th Physics Chapters
- Physics Mechanical Properties of Solids
- NCERT Class 11 Physics
- NCERT Class 11 Notes
- NCERT Notes
- Physics Motion in Plane
- Physics Mechanical Properties of Fluids
- Physics Motion in Straight Line
- Physics System of Particles and Rotational Motion
- Physics Oscillations
- Physics Waves
- Physics Thermal Properties of Matter
- Physics Motion
- Physics Gravitation
- Physics Thermodynamics
- Physics Work, Energy and Power
- Physics Units and Measurement
- Physics Laws of Motion