Simple Pendulum Explained Simply with Time Period, SHM, Energy, and More

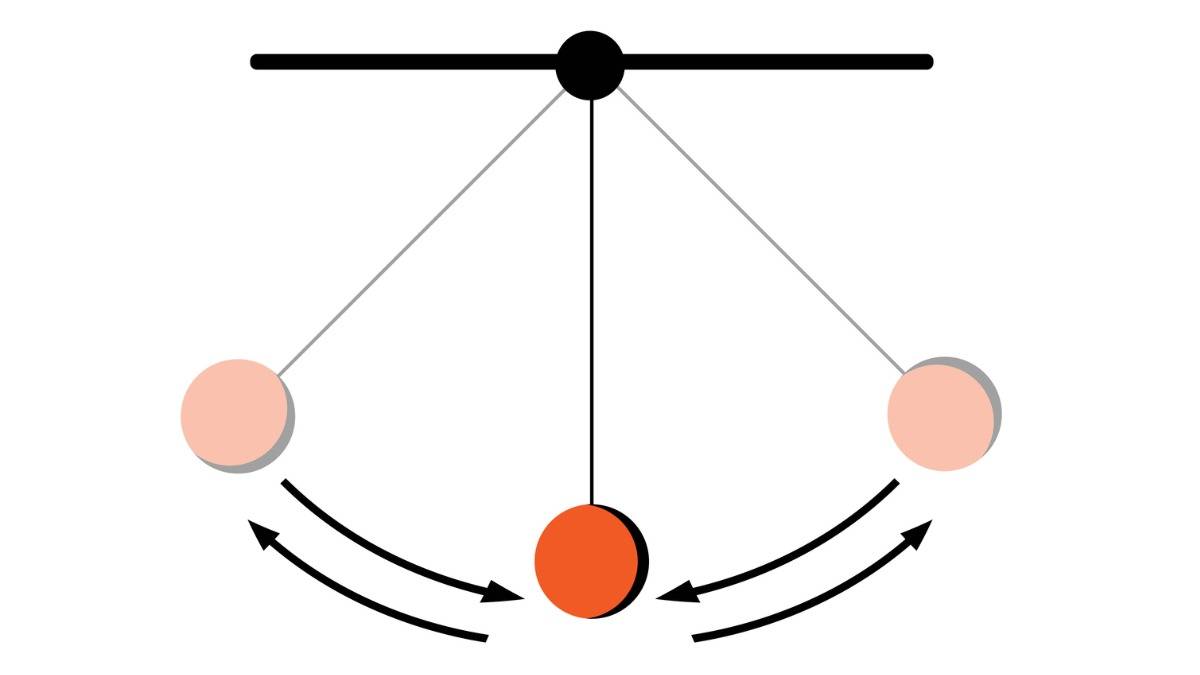
A simple pendulum is simply a weight hanging from a string. It swings back and forth. For small swings, it follows a predictable pattern that demonstrates Simple Harmonic Motion. The time for one complete swing depends only on:

• How long the string is
• How strong gravity is

Main Components of a Simple Pendulum

• A simple pendulum comprises a point mass. We call that a bob. 
• It is suspended from a fixed point by a massless, inextensible string. 
• The string is attached to a fixed surface.

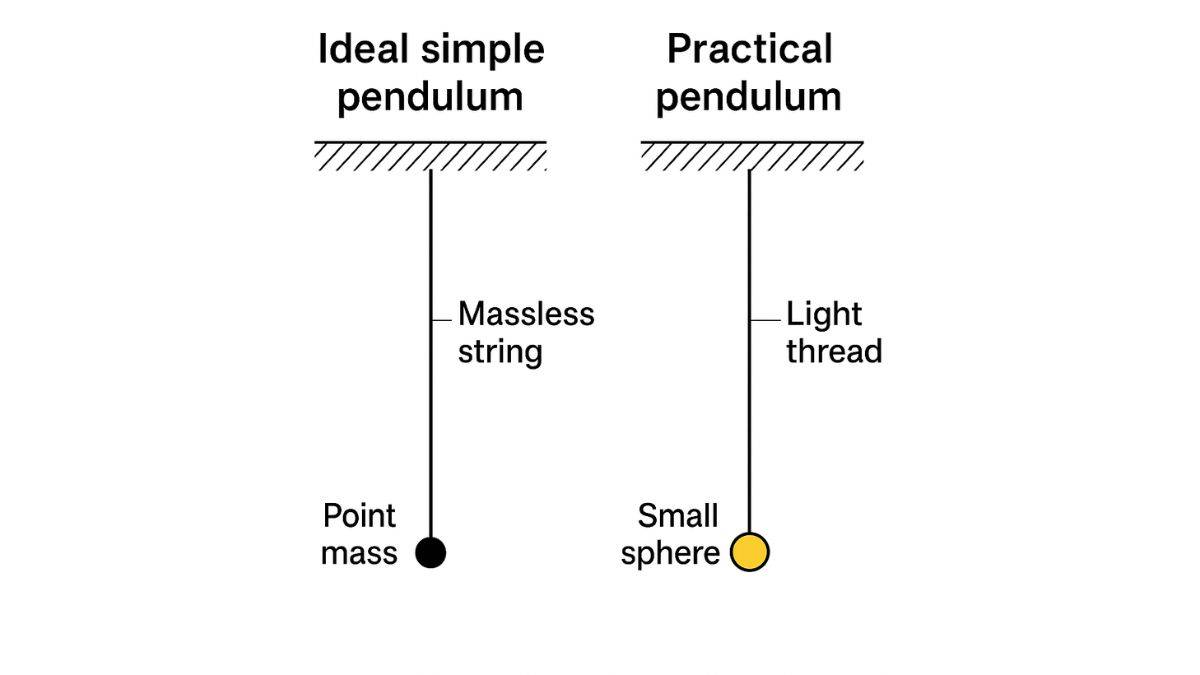
Ideal vs Real Simple Pendulum

Pendulums are of various types. In the context of simple pendulums taught in Class 11, we can look into two main ones. 

1. Ideal Simple Pendulum: This is a theoretical model that assumes a point mass with negligible mass and a perfectly flexible, weightless string. The oscillation occurs in a vacuum without air resistance. The NCERT Physics Class 11 textbook focuses on explaining an ideal simple pendulum. 
2. Practical Simple Pendulum: This is a real-world approximation, such as a small, dense sphere attached to a light thread. This distinction is crucial for understanding the physics of the simple pendulum, as well as the formula. 

 

 

The simple pendulum is a fundamental concept in physics that serves as a bridge to understanding the principles of simple harmonic motion (SHM). The basic idea behind this periodic motion is that when the string is displaced to a small angle, it swings back and forth under the influence of gravity. Additionally, go through the Gravitation Class 11 Notes.

It’s the restoring force that’s behind the simple pendulum’s motion.

When the bob displaces, gravity, acting along the swing’s arc of movement, pulls it back towards its lowest point. That point is also the equilibrium position, where all common forces acting on it are negligible.  

A simple pendulum exhibits simple harmonic motion for small angular displacements.

We can represent that as $\left(\theta <{10}^{\circ }\right)$ .

When displaced by an angle $\theta$ , the restoring force is provided by the tangential component of gravity: $F=-mg\mathrm{s}\mathrm{i}\mathrm{n}\theta$

But, now, when it comes to small angle approximation (the displacement angle is too small)  $\theta ,\mathrm{s}\mathrm{i}\mathrm{n}\theta \approx \theta$ (expressed in radians), and $\theta =\frac{x}{l}$ , where $x$ is the arc length and $l$ is the pendulum length, we can substitute that into the restoring force as $F\approx -mg\theta =-mg\frac{x}{l}$

The force constant (that is based on SHM Force Law) is

$k=\frac{mg}{l}$

And, since the restoring force according to the SHM Force Law is $F=-kx$ , the motion that is SHM has an angular frequency

$\omega =\sqrt[]{\frac{k}{m}}=\sqrt[]{\frac{g}{l}}$

What Determines the Time Period of a Simple Pendulum's Swing?

The time period (T) is the time the simple pendulum takes to complete one full back-and-forth swing. 

This time period is affected by only two factors.

• Pendulum's length and 
• Acceleration due to gravity.

Formula for Time Period in Simple Pendulum

$T=\frac{2\pi }{\omega }=2\pi \sqrt[]{\frac{l}{g}}$

Formula for Frequency in Simple Pendulum

$n=\frac{1}{T}=\frac{1}{2\pi }\sqrt[]{\frac{g}{l}}$

The period depends only on length $l$ and acceleration due to gravity $g$ , independent of mass $m$ and amplitude (for small oscillations).

 

Remember, we brought up that difference between the ideal and the real simple pendulum earlier?

For an ideal simple pendulum, the time period will always have the expression $T=2\pi \sqrt[]{\frac{l}{g}}$ . But, when considering a simple pendulum, the time period changes under the conditions or scenarios outlined below. 

 

• Length Variation: $T\propto \sqrt[]{l}$ . If the length increases by a factor of $4,T$ doubles.
• Gravity Variation: $T\propto \frac{1}{\sqrt[]{g}}$ . On a planet with $g^{\text{'}}=\frac{g}{2},T$ increases by $\sqrt[]{2}$ .
• Temperature Effect: A wire suspending the bob expands with the temperature, $l=l_0(1+$ $\alpha \mathrm{\Delta }\theta )$ .

The fractional change in period is: $\frac{\mathrm{\Delta }T}{T}\approx \frac{1}{2}\alpha \mathrm{\Delta }\theta$

For $\alpha =12\times {10}^{-6}/{}^{\circ }\mathrm{C},\mathrm{\Delta }\theta ={20}^{\circ }\mathrm{C},\mathrm{\Delta }T\approx 10.3\mathrm{s}/$ day.

• Liquid Immersion: If the bob (density $\rho$ ) is immersed in a liquid (density $\sigma <\rho$ ), effective gravity is: $g^{\text{'}}=g\left(1-\frac{\sigma }{\rho }\right)$

New period: $T^{\text{'}}=T\sqrt[]{\frac{\rho }{\rho -\sigma }}$ .

 

• Electric Field: For a charged bob $\left(q\right)$ in a vertical electric field $E$ (upward), effective gravity is: $g^{\text{'}}=g-\frac{qE}{m}$

Period: $T=2\pi \sqrt[]{\frac{l}{g-\frac{qE}{m}}}$

If $E$ is downward, $g^{\text{'}}=g+\frac{qE}{m}$ .

• Lift Motion

Lift at rest or constant velocity: $T=2\pi \sqrt[]{\frac{l}{g}}$ .

Lift accelerating upward with $a:T=2\pi \sqrt[]{\frac{l}{g+a}}$ .

Lift accelerating downward with $a:T=2\pi \sqrt[]{\frac{l}{g-a}}$ .

Free fall $(a=g):T\to \mathrm{\infty }$ , no oscillations 

• Horizontal Acceleration: If the suspension point accelerates horizontally with $a$ , effective gravity is: $g_{\mathrm{e}\mathrm{f}\mathrm{f}}=\sqrt[]{g^2+a^2}$

Period: $T=2\pi \sqrt[]{\frac{l}{\sqrt[]{g^2+a^2}}}$

The string inclines at $\theta ={\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}(a/g)$

• Circular Motion: If the suspension point moves in a circle of radius $r$ with speed $v$ , effective gravity is: $g_{\mathrm{e}\mathrm{f}\mathrm{f}}=\sqrt[]{g^2+{\left(\frac{v^2}{r}\right)}^2}$

Period: $T=2\pi \sqrt[]{\frac{l}{\sqrt[]{g^2+{\left(\frac{v^2}{r}\right)}^2}}}$

A pendulum with a period of 2 seconds is a second's pendulum.

On Earth ( $g=9.8\mathrm{m}/{\mathrm{s}}^2$ ):

$\begin{array}{c}T=2\pi \sqrt[]{\frac{l}{g}}=2\\ l=\frac{g}{{\pi }^2}\approx 0.993\mathrm{m}\approx 99.3\mathrm{c}\mathrm{m}\end{array}$

On the Moon ( $g_{\text{moon}}=\frac{g}{6}$ ), $l\approx 16.55\mathrm{c}\mathrm{m}$ .

The total mechanical energy of the simple pendulum is conserved (when you consider there is no air resistance).

But, it's essential to recognise that energy continually transforms between kinetic and potential forms.  

The bob's potential energy at angular displacement $\theta$ is: $U=mgl(1-\mathrm{c}\mathrm{o}\mathrm{s}\theta )$

At the mean position $(\theta =0),U=0$ . At the extreme position, $U_{\mathrm{m}\mathrm{a}\mathrm{x}}=mgl\left(1-\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_0\right)$ , where ${\theta }_0$ is the amplitude.

Kinetic energy at the mean position is $K_{\mathrm{m}\mathrm{a}\mathrm{x}}=mgl\left(1-\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_0\right)$

Total energy is conserved: $E=mgl\left(1-\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_0\right)$

Work done in displacing the pendulum to angle $\theta$ equals the potential energy $U$ .

 

For large $\theta ,\mathrm{s}\mathrm{i}\mathrm{n}\theta \ne \theta$ , and the motion is oscillatory but not SHM. The period increases slightly: $T\approx 2\pi \sqrt[]{\frac{l}{g}}\left[1+\frac{1}{16}{\theta }_0^2\right]$

For large amplitudes, numerical methods or series approximations are used.

 

Here are some key aspects to remember about a simple pendulum. 

• The Restoring Force is proportional to displacement for small angles. That ensures SHM.
• The time period of a simple pendulum is unaffected by the bob's mass.
• Simple harmonic motion holds only for small angular displacements in a simple pendulum.