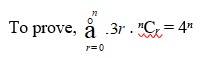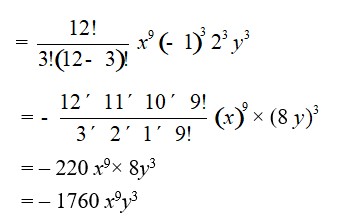12. Find a, b and n in the expansion of (a + b)n if the first three terms of the expansion are 729, 7290 and 30375, respectively.

1.The general term of the expansion (a + b)n is given by Tr +1 = nCran–rbr So, T1 = nC0an = an T2 = nC1an-1b = n!1!(n−1)! an-1 b = n×(n−1)!(n−1)! an-1b = nan-1b T3 = nC2an-2b2 = n!2!(n−2)[! an-2b2 = n ×(n−1)×(n−2)!2×1×(n−2)! an-2b2 = n(n−1)2 an-2b2 Given, T1 = 729 =>an = 729 ------------------ (1) T2 = 7290 =>nan–1b = 7290 ------------- (2) T3 = 30375 => n(n−1)2 an–2b2 = 30375 ------------------- (3) Dividing equation (2) by (1) we get, nan−1ban = 7290729 => nba = 10 Similarly dividing equation (3) by (2) we get, n(n−1)2 an–2b2 ÷ nan–1b = 303757290 => n(n−1)2 an–2b2× 1nan−1b = 303757290 => n(n−1)an−2b2 × 1nan−1b = 303757290 × 2 => (n−1)ba = 25′ ×26 => nba −ba = 253 => 10 – ba = 253 [since, nba = 10] => ba = 10 – 253 = 30−253 = 53 --------------- (5) Putting equation (5) in (4) we get, n× 53 = 10 =>n = 10 × 35 =>n = 6 So putting the value of n in equation (1) we get, a6 = 729 =>a6= 36 =>a = 3 And putting a = 3 in equation (5) we get, ba = 53 =>b = 53 ×a = 53 × 3 = 5

1. Show that 9n+1– 8n – 9 is divisible by 64, whenever n is a positive integer.

1. For a number x to be divisible by y, we can write x as a factor of y i.e., x = ky where k is some natural number. Thus in order for 9n+1 – 8n – 9 to be divisible by 64 we need to show that 9n+1 – 8n – 9 = 64k where k is some natural number. We have, by binomial theorem (1 + a)m = mC0 + mC1 (a) + mC2 (a)2 + mC3 (a)3 + ………… + mCm (a)m Putting, a = 8 and m = n + 1 (1 + 8)n+1 = n+1C0 + n+1C1.8 + n+1C2.82 + n+1C3.83 + ……. + n+1Cn+1. (8)n+1 => 9n+1= 1 + (n + 1)8 + 82× [n+1C2 + n+1C3.8 + ………. + n+1Cn+1. (8)n+1–2] [since, n+1C0 = 1, n+1C1= n + 1] => 9n+1 = 1 + 8n + 8 + 64 × [n+1C2 + n+1C3.8 + ………. + n+1Cn+1. (8)n+1-2] => 9n+1 – 8n – 9 = 64 × [n+1C2 + n+1C3.8 + ………. + 8n–1] [since, n+1Cn+1 = 1] => 9n+1 – 8n – 9 = 64k, where k = n+1C2 + n+1C3.8 + ………. + 8n–1 is a natural number. This shows that 9n+1 – 8n – 9 is divisible by 64

2. Prove that ∑r=0n3r nCr=4n.

2. By binomial theorem, (a + b)n = nC0 (a)n (b)0 + nC1 (a)n–1 (b)1 + …………. + nCr (a)n–r (b)r + …………… + nCn (a)n–n (b)n Where, b0 = 1 = an–n So, (a + b)n = nCr (a)n–r (b)r Putting a = 1 and b = 3 such that a + b = 4, we can rewrite the above equation as (1 + 3)n = nCr (1)n–r.3r =>4n = ? r=0.3r .nCr Hence proved.

4. a5b7in (a – 2b)12.

4. Let a5b7 occurs in (r + 1)th term of [removed]a – 2b)12. Now, Tr+1 = 12Cra12-r (–2b)r = (–1)r12Cra12–r . 2r. br Comparing indices of a and b in Tr-1 with a5 and b7 we get, r = 7 So, co-efficient of a5b7 is (–1)712C7 27

Write the general term in the expansion of 5. (x2–y)6

5. Let (r + 1)th term be the general term of (x2–y)6. So, Tr-1 = 6Cr (x2)6-r (-y)r = (–1)r .6Cr . x12−r . yr

Class 11 Maths Ch 7 Binomial Theorem NCERT Solutions | Step-by-Step Guide

Updated on Sep 18, 2025 17:12 IST

By Pallavi Pathak, Assistant Manager Content

Class 11 Maths Chapter 7 Binomial Theorem covers the calculation techniques of higher powers of binomials. The binomial theorem helps in such calculations. Ch 7 Class 11 Maths provides an easy way to expand ${(a + b)}^{n}$ , where n is an integer or a rational number. This chapter only covers the binomial theorem for positive integral indices.
Chapter 7 Class 11 Maths NCERT solutions are prepared by the subject matter experts at Shiksha. It is a reliable source where the solutions are given in a step-by-step format. It helps students develop problem-solving skills and gain confidence in solving NCERT questions. The solutions are ideal to score high in the CBSE Board exam and competitive exam like the JEE Main exam.
For all chapter notes of Class 11 Maths, including important topics and solved examples, Class 11 students can Explore Here. The notes are aligned with the latest CBSE updates.

Table of content

Overview of Binomial Theorem – Class 11 Maths Chapter 7
Chapter 7 Binomial Theorem : Key Topics, Weightage
Important Formulas of Ch 7 Maths Class 11 Binomial Theorem
Chapter 7 Binomial Theorem NCERT Solution PDF: Download PDF for Free
Chapter 7 Binomial Theorem Exercise-wise Solution
Chapter 7 Binomial Theorem Exercise 7.1 Solutions
Chapter 7 Binomial Theorem Exercise 7.2 Solutions
Chapter 7 Binomial Theorem Miscellaneous Exercise Solutions
Binomial Theorem - FAQs

Overview of Binomial Theorem – Class 11 Maths Chapter 7

Ch 7 Maths Class 11 is a short chapter. Here is a quick summary of Binomial Theorem - Chapter 7 Class 11 Maths:

The chapter covers the Binomial Theorem, which allows the expansion of a binomial for any positive integral n. Mathematically, it is shown as - ${(a + b)}^{n} = C_{0}^{n} a^{n} + C_{1}^{n} a^{n - 1} b + C_{2}^{n} a^{n - 2} b^{2} + \dots + C_{r}^{n} a^{n - r} b^{r} + C_{n}^{n} b^{n}$
It also introduces Pascal’s triangle, which is an array in which the coefficients of the expansions are arranged.

In case you are looking for NCERT notes of Physics, Chemistry & Maths of class 11 for quick revision. You must check here.

Chapter 7 Binomial Theorem : Key Topics, Weightage

In the Ch 7 Class 11 Maths Binomial Theorem, the students should thoroughly understand the binomial expansion, the middle terms, finding general terms, and applications of the theorem. This is not a very high-weightage chapter for JEE Mains, but Class 11 students need to understand this chapter well to score good marks in the entrance exams later. Here are the topics covered in this chapter:

Exercise	Topics Covered
7.1	Introduction
7.2	Binomial Theorem for Positive Integral Indices

Chapter 7 Class 11 Maths Binomial Theorem Weightage in JEE Mains exam

Exam	Number of Questions	Weightage
JEE Mains	1 question	3.3%

Important Formulas of Ch 7 Maths Class 11 Binomial Theorem

Important Terms and Formulae for Binomial Theorem

Binomial Expansion

$(a + b)^{n} = \sum_{r = 0}^{n} (\binom{n}{r}) a^{n - r} b^{r}$

where $\binom{n}{r} = \frac{n!}{r!(n-r)!}$

General Term

$T_{r + 1} = (\binom{n}{r}) a^{n - r} b^{r}$

Middle Term(s)

- If $n$ is even: $T_{\frac{n}{2}+1}$
- If $n$ is odd: Two middle terms: $T_{\frac{n+1}{2}}$ and $T_{\frac{n+3}{2}}$

4. Sum of Binomial Coefficients

$\sum_{r=0}^{n} \binom{n}{r} = 2^n$

5. Approximation Formula (for small $x$ )

$(1 + x)^n \approx 1 + nx + \frac{n(n-1)}{2}x^2$

Chapter 7 Binomial Theorem NCERT Solution PDF: Download PDF for Free

Students must download the free PDF of the Class 11 Maths Chapter 7 from the link given below. The solutions are well-structured and help students to improve their school exam, CBSE Board exam, and JEE Mains exam preparation.
Class 12 Math Chapter 7 Binomial Theorem Solution PDF: Free PDF Download

Chapter 7 Binomial Theorem Exercise-wise Solution

Class 11 Binomial Theorem is a very important mathematical concept that provides a systematic method for expanding expressions of the form $(a + b)^n$ , where $n$ is a positive integer. Class 11 Chapter 7 Binomial theorem consists of several exercises and problem based on taught concepts. Earlier this chapter was numbered as chapter 8 in old NCERT Textbooks. Exercise 8.1 includes expansion of $(a+b)^n$

Chapter 7 Binomial Theorem Exercise 7.1 Solutions

Binomial Theorem Exercise 7.1 focuses on the basic principles and applications of understanding the General Expansion, Binomial Coefficients, General Term Formula, and other related concepts. Candidates can check the Binomial Therom class 11 Exercise7.1 solution below;

Binomial Theorem Exercise 7.1 NCERT Solutions

Expand each of the expressions in Exercises 1 to 2.

Q1. (1–2x)⁵

A.1. (1 – 2x)⁵

By using binomial theorem we have,

= ⁵C₀ (1)⁵+⁵C₁ (1)⁴ (-2x) + ⁵C₂ (1)³ (-2x)²+⁵C₃ (1)² (-2x)³+⁵C₄ (1)¹ (-2x)⁴+⁵C₅ (-2x)⁵

= $(\frac{5!}{0! (5 - 0)!} ′ 1)$ + $[\frac{5!}{1! (5 - 1)!}' 1' (- 2 x)]$ +[x1× (4x²)] + $[\frac{5!}{3! (5 - 3)!}' 1' (- 8 x^{3})]$ + $[\frac{5!}{4! (5 - 4)!}' 1' (16 x^{4})]$ + $[\frac{5!}{5! (5 - 5)!}' (- 32 x^{5})]$

= 1 + $[\frac{5′ 4!}{1′ 4!}' (- 2 x)]$ + $[\frac{5′ 4′ 3!}{2′ 1′ 3!} \times 4 x^{2}]$ + $[\frac{5′ 4′ 3!}{3!' 2!} \times (- 8 x^{3})]$ + $[\frac{5′ 4!}{4!' 1} \times 16 x^{4}]$ + [1 × (-32x⁵)]

= 1 + [5 × (–2x)] + [10 × 4x²] + [10 × (–8x³)] + [5 × 16x⁴] + [–32x⁵]

= 1 – 10x + 40x² – 80x³ + 80x⁴ – 32x⁵

Q2. ${(\frac{2}{x} - \frac{x}{2})}^{5}$

A.2. ${(\frac{2}{x} - \frac{x}{2})}^{5}$

Using (x – y)ⁿ

= ⁵C₀ ${(\frac{2}{x})}^{5}$ – ⁵C₁ ${(\frac{2}{x})}^{4}$ $(\frac{x}{2})$ + ⁵C₂ ${(\frac{2}{x})}^{3}$ ${(\frac{x}{2})}^{2}$ –⁵C₃ ${(\frac{2}{x})}^{2}$ ${(\frac{x}{2})}^{3}$ + ⁵C₄ $(\frac{2}{x})$ ${(\frac{x}{2})}^{4}$ – ⁵C₅ ${(\frac{x}{2})}^{5}$

= $[\frac{5!}{0! (5 - 0)!} \frac{′3 2}{x^{5}}]$ – $[\frac{5!}{1! (5 - 1)!}' \frac{16}{x^{4}} \times \frac{x}{2}]$ + $[\frac{5!}{2! (5 - 2)!}' \frac{8}{x^{3}}' \frac{x^{2}}{4}]$ – $[\frac{5!}{3! (5 - 3)!}' \frac{4}{x^{2}}' \frac{x^{3}}{8}]$ + $[\frac{5!}{4! (5 - 4)!}' \frac{x}{2}' \frac{x^{4}}{16}]$ – $[\frac{5!}{5! (5 - 5)!}' \frac{x^{5}}{32}]$

= $[1' \frac{32}{x^{5}}]$ – $[\frac{5' 4!}{1' 4!}' \frac{8}{x^{3}}]$ + $[\frac{5' 4′ 3!}{2' 1′ 3!}' \frac{2}{x}]$ – $[\frac{5′ 4′ 3!}{3!' 2!} \times \frac{x}{2}]$ + $[\frac{5′ 4!}{4!' 1!}' \frac{x^{3}}{8}]$ – $[1′ \frac{x^{5}}{32}]$

= $\frac{32}{x^{5}}$ – $\frac{40}{x^{3}}$ + $\frac{20}{x}$ – 5x + $\frac{5}{8} x^{3}$ – $\frac{x^{5}}{32}$

Using binomial theorem, evaluate each of the following:

Q3. (102)⁵

A.3. (102)⁵ = (100 + 2)⁵

By using binomial theorem,

= ⁵C₀(100)⁵ + ⁵C₁(100)⁴(2) + ⁵C₂(100)³(2)² + ⁵C₃(100)²(2)³ + ⁵C₄(100)(2)⁴ + ⁵C₅(2)⁵

= $[\frac{5!}{0! (5 - 0)!}' 10000000000]$ + $[\frac{5!}{1! (5 - 1)!}' 00000000' 2]$ + $[\frac{5!}{2! (5 - 2)!}' 1000000' 4]$ + $[\frac{5!}{3! (5 - 3)!}' 10000' 8]$ + $[\frac{5!}{4! (5 - 4)!}' 100' 16]$ + $[\frac{5!}{5! (5 - 5)!}' 32]$

= [1 × 10000000000] + $[\frac{5′ 4!}{1′ 4!}' 00000000]$ + $[\frac{5′ 4′ 3!}{2′ 1′ 3!}' 4000000]$ + $[\frac{5′ 4′ 3!}{3!' 2!}' 80000]$ + $[\frac{5′ 4!}{4!' 1!}' 1600]$ + [1 × 32]

= 10000000000 + 1000000000 + 40000000 + 800000 + 8000 + 32

= 11040808032

Q4. (101)⁴

A.4. (101)⁴ = (100 + 1)⁴

By binomial theorem we get,

= ⁴C₀(100)⁴ + ⁴C₁(100)³(1) + ⁴C₂(100)²(1)² + ⁴C₃(100)(1)³ + ⁴C₄(1)⁴

= $[\frac{4!}{0! (4 - 0)!}' 00000000]$ + $[\frac{4!}{1! (4 - 1)!}' 000000' 1]$ + $[\frac{4!}{2! (4 - 2)!}' 10000' 1]$ + $[\frac{4!}{3! (4 - 3)!}' 100' 1]$ + $[\frac{4!}{4! (4 - 4)!}' 1]$

= [1 × 100000000] + $[\frac{4′ 3!}{1′ 3!}' 1000000]$ + $[\frac{4′ 3′ 2!}{2′ 1′ 2!}' 10000]$ + $[\frac{4′ 3!}{3!' 1!}' 100]$ +[1 × 1]

= 100000000 + 4000000 + 60000 + 400 + 1

= 104060401

Q5. (99)⁵

A.5. (99)⁵ = (100 – 1)⁵

By binomial theorem we get,

= ⁵C₀(100)⁵ –⁵C₁(100)⁴(1) + ⁵C₂(100)³(1)²–⁵C₃(100)²(1)³ + ⁵C₄(100)(1)⁴ –⁵C₅(1)⁵

= $[\frac{5!}{0! (5 - 0)!}' 10000000000]$ – $[\frac{5!}{1! (5 - 1)!}' 00000000' 1]$ + $[\frac{5!}{2! (5 - 2)!}' 000000' 1]$ – $[\frac{5!}{3! (5 - 3)!}' 10000' 1]$ + $[\frac{5!}{4! (5 - 4)!}' 100' 1]$ – $[\frac{5!}{5! (5 - 5)!}' 1]$

= [1 × 10000000000] – $\frac{5′ 4!}{1′ 4!}' 00000000$ + $[\frac{5′ 4′ 3!}{2′ 1′ 3!}' 100000]$ – $[\frac{5′ 4′ 3!}{3!' 2!}' 10000]$ + $[\frac{5′ 4!}{4!' 1!}' 100]$ – [1 × 1]

= 10000000000 – 500000000 + 10000000 – 100000 + 500 – 1

= 10010000500 – 500100001

= 9509900499

Q6. Using Binomial Theorem, indicate which number is larger (1.1)¹⁰⁰⁰⁰or 1000.

A.6. We know that,

(1.1)¹⁰⁰⁰⁰ = (1 + 0.1)¹⁰⁰⁰⁰

By using binomial theorem,

= ¹⁰⁰⁰⁰C₀(1)¹⁰⁰⁰⁰ + ¹⁰⁰⁰⁰C₁ (1)^{(10000 – 1)} (0.1) + other positive terms

= $[\frac{10000!}{0! (10000 - 0)!}' 1]$ + $[\frac{10000!}{1! (10000 - 1)!}' 1' 0.1]$ + other positive terms

= [1 × 1] + $[\frac{1000 0′ 9999!}{1′ 9999!}' 0.1]$ + other positive terms

= 1 + 1000 + other positive terms

= 1001 + other positive terms

Hence, (1.1)¹⁰⁰⁰⁰> 1000

Q7. Find (a + b)4– (a – b)4. Hence, evaluate ${(\sqrt3 +\sqrt2)}^{4} - {(\sqrt3 -\sqrt2)}^{4} .$

A.7. Using binomial theorem we have,

(a + b)⁴ – (a – b)⁴

= [⁴C₀a⁴ + ⁴C₁a³b + ⁴C₂a²b² + ⁴C₃ab³ + ⁴C₄b⁴] – [⁴C₀a⁴ – ⁴C₁a³b + ⁴C₂a²b² – ⁴C₃ab³ + ⁴C₄b⁴]

= ⁴C₀a⁴ + ⁴C₁a³b + ⁴C₂a²b² + ⁴C₃ab³ + ⁴C₄b⁴– ⁴C₀a⁴ + ⁴C₁a³b – ⁴C₂a²b² + ⁴C₃ab³ – ⁴C₄b⁴

= [2 ×⁴C₁a³b] + [2 ×⁴C₃ab³]

= $[2′ \frac{4!}{1! (4 - 1)!} a^{3} b]$ + $[2′ \frac{4!}{3! (4 - 3)!} a b^{3}]$

= $[2′ \frac{4′ 3!}{1′ 3!} a^{3} b]$ + $[2′ \frac{4′ 3!}{3!' 1!} a b^{3}]$

= 8a³b + 8ab³

Hence putting a = √3 and b = √2 we have,

${(\sqrt3 +\sqrt2)}^{4}$ – ${(\sqrt3 -\sqrt2)}^{4}$

= 8 ${(\sqrt3)}^{3} (\sqrt2)$ + 8 $(\sqrt3)$ ${(\sqrt2)}^{3}$

= (8 × 3 √3 ×√2 )+ (8 × √3 × 2 √2 )

= 24 √6 + 16 √6

= 40 √6

Q8. Find (x + 1)6+ (x – 1)6. Hence or otherwise evaluate ${(\sqrt2 + 1)}^{6} + {(\sqrt2 - 1)}^{6} .$

A.8. By binomial expansion we have,

${(x + 1)}^{6}$ + ${(x - 1)}^{6}$

= [⁶C₀(x⁶) + ⁶C₁(x⁵)(1) + ⁶C₂(x⁴)(1)² + ⁶C₃(x³)(1)³ + ⁶C₄(x²)(1)⁴ + ⁶C₅(x)(1)⁵ + ⁶C₆(1)⁶] + [⁶C₀(x⁶) – ⁶C₁(x⁵)(1) + ⁶C₂(x⁴)(1)² – ⁶C₃(x³)(1)³ + ⁶C₄(x²)(1)⁴ – ⁶C₅(x)(1)⁵ + ⁶C₆(1)⁶]

= ⁶C₀(x⁶) + ⁶C₁(x⁵)(1) + ⁶C₂(x⁴)(1)² + ⁶C₃(x³)(1)³ + ⁶C₄(x²)(1)⁴ + ⁶C₅(x)(1)⁵ + ⁶C₆(1)⁶ + ⁶C₀(x⁶) – ⁶C₁(x⁵)(1) + ⁶C₂(x⁴)(1)² – ⁶C₃(x³)(1)³ + ⁶C₄(x²)(1)⁴ – ⁶C₅(x)(1)⁵ + ⁶C₆(1)⁶

= 2 × [⁶C₀(x⁶) + ⁶C₂(x⁴)(1)² + ⁶C₄(x²)(1)⁴ + ⁶C₆(1)⁶]

= 2 × $[(\frac{6!}{0! (6 - 0)!}' x^{6}) + (\frac{6!}{2! (6 - 2)!} \frac{6!}{2! (6 - 2)!} + x^{4}' 1)$ + $(\frac{6!}{4! (6 - 4)!}' x^{2}' 1) + (\frac{6!}{6! (6 - 6)!}' 1)]$

= 2 × [(1 × $x^{6}$ ) + $(\frac{6′ 5′ 4!}{2′ 1′ 4!}' x^{4}) + (\frac{6′ 5′ 4!}{4!' 2!}' x^{2})$ + (1 × 1)]

= 2[ $x^{6}$ + 15 $x^{4}$ + 15 $x^{2}$ + 1]

Hence putting x = √2 we have,

( √2 + 1)⁶ + ( √2 – 1)⁶

= 2 × [ ${(\sqrt2)}^{6}$ + 15 ${(\sqrt2)}^{4}$ + 15 ${(\sqrt2)}^{2}$ + 1]

= 2 × [2³ + (15 x 2²) + (15 x 2) + 1]

= 2 × [8 + 60 + 30 + 1]

= 2 × 99

= 198

Q9. Show that 9ⁿ⁺¹– 8n – 9 is divisible by 64, whenever n is a positive integer.

A.9. For a number x to be divisible by y, we can write x as a factor of y i.e., x = ky where k is some natural number. Thus in order for 9ⁿ⁺¹ – 8n – 9 to be divisible by 64 we need to show that 9ⁿ⁺¹ – 8n – 9 = 64k where k is some natural number.

We have, by binomial theorem

(1 + a)^m = ^mC₀ + ^mC₁(a) + ^mC₂(a)² + ^mC₃(a)³ + ………… + ^mC_m(a)^m

Putting, a = 8 and m = n + 1

(1 + 8)ⁿ⁺¹ = ⁿ⁺¹C₀ + ⁿ⁺¹C₁.8 + ⁿ⁺¹C₂.8² + ⁿ⁺¹C₃.8³ + …….. + ⁿ⁺¹C_n₊₁.(8)ⁿ⁺¹

=> 9ⁿ⁺¹= 1 + (n + 1)8 + 8²×[ⁿ⁺¹C₂ + ⁿ⁺¹C₃.8 + ……….. + ⁿ⁺¹C_n₊₁.(8)ⁿ^+1–2] [since, ⁿ⁺¹C₀ = 1, ⁿ⁺¹C₁= n + 1]

=> 9ⁿ⁺¹ = 1 + 8n + 8 + 64 × [ⁿ⁺¹C₂ + ⁿ⁺¹C₃.8 + ……….. + ⁿ⁺¹C_n₊₁.(8)ⁿ^+1-2]

=> 9ⁿ⁺¹ – 8n – 9 = 64 × [ⁿ⁺¹C₂ + ⁿ⁺¹C₃.8 + ……….. + 8ⁿ^–1][since, ⁿ⁺¹C_n₊₁ = 1]

=> 9ⁿ⁺¹ – 8n – 9 = 64k,

where k = ⁿ⁺¹C₂ + ⁿ⁺¹C₃.8 + ……….. + 8ⁿ^–1 is a natural number.

This shows that 9ⁿ⁺¹ – 8n – 9 is divisible by 64

Q10. Prove that $\sum_{r = 0}^{n} 3^{r}^{n} C_{r} = 4^{n} .$

A.10.

By binomial theorem,

(a + b)ⁿ = ⁿC₀(a)ⁿ(b)⁰ + ⁿC₁(a)ⁿ^–1(b)¹ + ………….. + ⁿC_r(a)ⁿ^–r(b)^r + …………… + ⁿC_n(a)ⁿ^–n(b)ⁿ

Where, b⁰ = 1 = aⁿ^–n

So, (a + b)ⁿ = ⁿC_r(a)ⁿ^–r(b)^r

Putting a = 1 and b = 3 such that a + b = 4 , we can rewrite the above equation as

(1 + 3)ⁿ = ⁿC_r(1)ⁿ^–r.3^r

=>4ⁿ = $\sum_{r = 0} . 3 r$ .ⁿC_r

Hence proved.

Commonly asked questions

12. Find a, b and n in the expansion of (a + b)ⁿ if the first three terms of the expansion are 729, 7290 and 30375, respectively.

1.The general term of the expansion (a + b)ⁿ is given by

T_r₊₁ = ⁿC_raⁿ^–rb^r

So, T₁ = ⁿC₀aⁿ = aⁿ

T₂ = ⁿC₁aⁿ^-1b = $\frac{n!}{1! (n - 1)!}$ aⁿ^-1 b = $\frac{n \times (n - 1)!}{(n - 1)!}$ aⁿ^-1b = naⁿ^-1b

T₃ = ⁿC₂aⁿ^-2b² = $\frac{n!}{2! (n - 2) [!}$ aⁿ^-2b² = $\frac{n \times (n - 1) \times (n - 2)!}{2 \times 1 \times (n - 2)!}$ aⁿ^-2b² = $\frac{n (n - 1)}{2}$ aⁿ^-2b²

Given,

T₁ = 729

=>aⁿ = 729 ------------------ (1)

T₂ = 7290

=>naⁿ^–1b = 7290 ------------- (2)

T₃ = 30375

=> $\frac{n (n - 1)}{2}$ aⁿ^–2b² = 30375 ------------------- (3)

Dividing equation (2) by (1) we get,

$\frac{n a^{n - 1} b}{a^{n}}$ = $\frac{7290}{729}$

=> $\frac{n b}{a}$ = 10

Similarly dividing equation (3) by (2) we get,

$\frac{n (n - 1)}{2}$ aⁿ^–2b² ÷ naⁿ^–1b = $\frac{30375}{7290}$

=> $\frac{n (n - 1)}{2}$ aⁿ^–2b²× $\frac{1}{n a^{n - 1} b}$ = $\frac{30375}{7290}$

=> $n (n - 1) a^{n - 2} b^{2}$ × $\frac{1}{n a^{n - 1} b}$ = $\frac{30375}{7290}$ × 2

=> $\frac{(n - 1) b}{a}$ = $\frac{2 5′ \times 2}{6}$

=> $\frac{n b}{a}$ $- \frac{b}{a}$ = $\frac{25}{3}$

=> 10 – $\frac{b}{a}$ = $\frac{25}{3}$ [since, $\frac{n b}{a}$ = 10]

=> $\frac{b}{a}$ = 10 – $\frac{25}{3}$

= $\frac{30 - 25}{3}$

= $\frac{5}{3}$ --------------- (5)

Putting equation (5) in (4) we get,

n× $\frac{5}{3}$ = 10

=>n = 10 × $\frac{3}{5}$

=>n = 6

So putting the value of n in equation (1) we get,

a6 = 729

=>a⁶= 36

=>a = 3

And putting a = 3 in equation (5) we get,

$\frac{b}{a}$ = $\frac{5}{3}$

=>b = $\frac{5}{3}$ ×a

= $\frac{5}{3}$ × 3

= 5

1. Show that 9ⁿ⁺¹– 8n – 9 is divisible by 64, whenever n is a positive integer.

1. For a number x to be divisible by y, we can write x as a factor of y i.e., x = ky where k is some natural number. Thus in order for 9ⁿ⁺¹ – 8n – 9 to be divisible by 64 we need to show that 9ⁿ⁺¹ – 8n – 9 = 64k where k is some natural number.

We have, by binomial theorem

(1 + a)^m = ^mC₀ + ^mC₁ (a) + ^mC₂ (a)² + ^mC₃ (a)³ + ………… + ^mC_m (a)^m

Putting, a = 8 and m = n + 1

(1 + 8)ⁿ⁺¹ = ⁿ⁺¹C₀ + ⁿ⁺¹C₁.8 + ⁿ⁺¹C₂.8² + ⁿ⁺¹C₃.8³ + ……. + ⁿ⁺¹C_n₊₁. (8)ⁿ⁺¹

=> 9ⁿ⁺¹= 1 + (n + 1)8 + 8²× [ⁿ⁺¹C₂ + ⁿ⁺¹C₃.8 + ………. + ⁿ⁺¹C_n₊₁. (8)ⁿ^+1–2] [since, ⁿ⁺¹C₀ = 1, ⁿ⁺¹C₁= n + 1]

=> 9ⁿ⁺¹ = 1 + 8n + 8 + 64 × [ⁿ⁺¹C₂ + ⁿ⁺¹C₃.8 + ………. + ⁿ⁺¹C_n₊₁. (8)ⁿ^+1-2]

=> 9ⁿ⁺¹ – 8n – 9 = 64 × [ⁿ⁺¹C₂ + ⁿ⁺¹C₃.8 + ………. + 8ⁿ^–1] [since, ⁿ⁺¹C_n₊₁ = 1]

=> 9ⁿ⁺¹ – 8n – 9 = 64k,

where k = ⁿ⁺¹C₂ + ⁿ⁺¹C₃.8 + ………. + 8ⁿ^–1 is a natural number.

This shows that 9ⁿ⁺¹ – 8n – 9 is divisible by 64

2. Prove that $\sum_{r = 0}^{n} 3^{r}^{n} C_{r} = 4^{n} .$

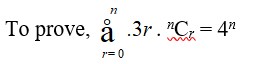
By binomial theorem,

(a + b)ⁿ = ⁿC₀ (a)ⁿ (b)⁰ + ⁿC₁ (a)ⁿ^–1 (b)¹ + …………. + ⁿC_r (a)ⁿ^–r (b)^r + …………… + ⁿC_n (a)ⁿ^–n (b)ⁿ

Where, b⁰ = 1 = aⁿ^–n

So, (a + b)ⁿ = ⁿC_r (a)ⁿ^–r (b)^r

Putting a = 1 and b = 3 such that a + b = 4, we can rewrite the above equation as

(1 + 3)ⁿ = ⁿC_r (1)ⁿ^–r.3^r

=>4ⁿ = $\underset{r = 0}{?} . 3 r$ .ⁿC_r

Hence proved.

4. a⁵b⁷in (a – 2b)¹².

4. Let a⁵b⁷ occurs in (r + 1)^th term of [removed]a – 2b)¹².

Now, T_r₊₁ = ¹²C_ra^12-r (–2b)^r

= (–1)^r¹²C_ra^12–r . 2^r. b^r

Comparing indices of a and b in T_r_-1 with a⁵ and b⁷ we get, r = 7

So, co-efficient of a⁵b⁷ is (–1)⁷¹²C₇ 2⁷

Write the general term in the expansion of

5. (x²–y)⁶

5. Let (r + 1)^th term be the general term of (x²–y)⁶.

So, T_r_-1 = ⁶C_r (x²)^6-r (-y)^r

= (–1)^r .⁶C_r . $x^{12 - r}$ . $y^{r}$

6. ( $x^{2} - y x)^{12}$ , x≠ 0.

6. Let (r + 1)th be the general term of ( $x^{2} - y x)^{12}$

So, T_r_-1 = ¹²C_r (x²)^12–r (–yx)^r

= (–1)^r¹²C_rx^24–2ry^rx^r

= (–1)^r¹²C_r $x^{24 - 2 r + r} y^{r}$

= (-1)^r¹²C_r $x^{24 - r} y^{r}$

7. Find the 4thterm in the expansion of (x – 2y)¹².

8. In the expansion of (1 + a)^m⁺ⁿ,prove that coefficients of aⁿ and aⁿ are equal.

8. The general term of the expansion (1 + a)^m⁺ⁿ is

T_r₊₁ = ^m⁺ⁿC_ra^r [since, 1^m^+n-r = 1]

At r = m we have,

T_m₊₁ = ^m⁺ⁿC_ma^m

= $\frac{(m + n)!}{m! (m + n - m)!}$ (a)^m

= $\frac{(m + n)!}{m! n!}$ a^m - (1)

Similarly at r = n we have,

T_n₊₁ = ^m⁺ⁿC_naⁿ

= $\frac{(m + n)!}{n! (m + n - n)!}$ (a)ⁿ

= $\frac{(m + n)!}{n! m!}$ aⁿ - (2)

Hence from (1) & (2),

Co-efficient of am = Co-efficient of aⁿ = $\frac{(m + n)!}{m! n!}$

9. The coefficients of the (r – 1)^th, r^thand (r + 1)^thterms in the expansion of (x + 1)ⁿ are in the ratio 1 : 3 : 5. Find n and r.

9. The general term of the expansion (x +1)ⁿ is

T_r₊₁ = ⁿC_rxⁿ^–r1^r

i.e. co-efficient of ${(r + 1)}^{t h}$ term = ⁿC_r

So, co-efficient of ${(r - 1)}^{t h}$ term =ⁿC_{(r–1) – 1} = ⁿC_r_{– 2}

Similarly, co-efficient of rth term = ⁿC_r_{– 1}

Given that, ⁿC_r_{– 2}:ⁿC_r_{– 1}: ⁿC_r = 1 : 3 : 5

We have,

= $\frac{1}{3}$

=> $\frac{n!}{(r - 2)! (n - r + 2)!}$ × $\frac{(r - 1)! (n - r + 1)!}{n!}$ = $\frac{1}{3}$

=> $\frac{(r - 1) (r - 2)! (n - r + 1)!}{(r - 2)! (n - r + 2) (n - r + 1)!}$ = $\frac{1}{3}$

=> $\frac{(r - 1)}{(n - r + 2)}$ = $\frac{1}{3}$

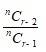
=> 3r – 3 = n – r + 2

=> 3r + r = n + 2 + 3

=> 4r = n + 5 -------------- (1)

And,

= $\frac{3}{5}$

=> $\frac{n!}{(r - 1)! (n - r + 1)!}$ × $\frac{r! (n - r)!}{n!}$ = $\frac{3}{5}$

=> $\frac{r (r - 1)! (n - r)!}{(r - 1)! (n - r + 1) (n - r)!}$ = $\frac{3}{5}$

=> $\frac{r}{n - r + 1}$ = $\frac{3}{5}$

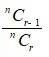
=> 5r = 3n – 3r + 3

=> 5r + 3r = 3n + 3

=> 8r = 3n + 3 ----------------------- (2)

Multiplying equation (1) by 2 and subtracting from equation (2) we get,

8r – 8r = 3n + 3 – (2n + 10)

=> 0 = 3n + 3 – 2n – 10

=> 0 = n – 7

=>n = 7

Putting n = 7 in equation (1) we get,

=> 4r = 7 + 5

=>r = $\frac{12}{4}$

=>r = 3

10. Prove that the coefficient of xⁿin the expansion of (1 + x)²ⁿis twice the coefficientof xⁿin the expansion of (1 + x)^2n-1.

10. General term of the expansion (1 + x)²ⁿ is

T_r₊₁ = ²ⁿC_r (1)^2n-r(x)^r

So, co-efficient of xⁿ (i.e. r = n) is ²ⁿC_n

Similarly general term of the expansion (1 + x)^2n–1 is

T_r₊₁ = ^2n-1C_r (1)^2n–1–rx^r

And co-efficient of xⁿ i.e. when r = n is ^2n-1C_n

Therefore,

$\frac{c o - e f f i c i e n t o f x^{n} i n {(1 + x)}^{2 n}}{c o - e f f i c i e n t o f x^{n} i n {(1 + x)}^{2 n - 1}}$

= $\frac{2 n!}{n! (2 n - n)!}$ ÷ $\frac{(2 n - 1)!}{n! (2 n - 1 - n)!}$

= $\frac{2 n!}{n! n!}$ × $\frac{n! (n - 1)!}{(2 n - 1)!}$

= $\frac{2 n}{n}$

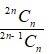
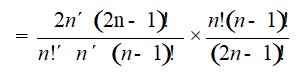
= 2

Thus, co-efficient of $x^{n}$ in ${(1 + x)}^{2 n}$ = 2x co-efficient of $x^{n}$ in ${(1 + x)}^{2 n - 1}$

11. Find a positive value of m for which the coefficient of x²in the expansion (1 + x)^mis 6.

11. The general term of the expansion ${(1 + x)}^{m}$ is given by,

T_r₊₁ = ^mC_r $1^{m - r} x^{r}$

= ^mC_rx^r

At r = 2,

T₂₊₁ = ^mC₂x²

Given that, co-efficient of x² = 6

=>^mC₂ = 6

=> $\frac{m!}{2! (m - 2)!}$ = 6

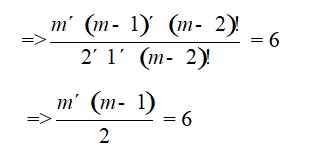
=>m² – m = 12

=>m² – m – 12 = 0

=>m² + 3m – 4m – 12 = 0

=>m (m + 3) – 4 (m+ 3) = 0

=> (m – 4) (m + 3) = 0

=>m = 4 and m = –3

Since, we need a positive value of m we have, m = 4

13. Find a if the coefficients of x²and x³in the expansion of (3 + ax)⁹are equal.

13. The general term of the expansion ${(3 + a x)}^{9}$ is

T_r₊₁ = ⁹C_r $3^{(9 - r)}$ ${(a x)}^{r}$

= ⁹C_r $3^{(9 - r)} a^{r} x^{r}$

At r = 2,

T₂₊₁ = ⁹C₂ $3^{(9 - 2)} a^{2} x^{2}$

= $\frac{9!}{2! (9 - 2)!}$ 3⁷a²x²

= $9′$ $8′$ $7!$ / $2′$ $1′$ $7!$ 3⁷a²x²

= 36 ×3⁷a²x²

At r = 3,

T₃₊₁ = ⁹C₃ $3^{(9 - 3)} a^{3} x^{3}$

= $\frac{9!}{3! (9 - 3)!}$ 3⁶a³x³

= 9'8'7'6!/3'2'1'6! 3⁶a³x³

= 84 ×3⁶a³x³

Given that,

Co-efficient of $x^{2}$ = co-efficient of $x^{3}$

=> 36 × $3^{7} a^{2}$ = 84 × $3^{6} a^{3}$

=> $\frac{a^{3}}{a^{2}}$ = 36' 3⁷^/84'3⁶

=> $a$ = $3′3/7$

= $\frac{9}{7}$

14. If a and b are distinct integers, prove that a – b is a factor of aⁿ– bⁿ, whenever n is a positive integer.

[Hint: write aⁿ= (a – b + b)ⁿ and expand]

14. For (a – b) to be a factor of aⁿ – b ⁿwe need to show (aⁿ – bⁿ) = (a – b)k as k is a natural number.

We have, for positive n

aⁿ = ${(a - b + b)}^{n}$ = ${[(a - b) + b]}^{n}$

=>aⁿ = ⁿC₀(a – b)ⁿ + ⁿC₁(a – b)^{n -}¹b + ⁿC₂(a – b)^{n –}²b² + ………… +ⁿC_n_-1 $(a - b) b^{n - 1}$ + ⁿC_nbⁿ

=>aⁿ= ${(a - b)}^{n}$ + ⁿC₁ ${(a - b)}^{n - 1} b$ + ⁿC₂ ${(a - b)}^{n - 2} b^{2}$ + …………….…+ ⁿC_n_-1 $(a - b) b^{n - 1}$ + $b^{n}$ [Since, ⁿC₀ = 1 and ⁿC_n = 1]

=> $a^{n} - b^{n}$ = ${(a - b)}^{n}$ +ⁿC₁ ${(a - b)}^{n - 1} b$ + ⁿC₂ ${(a - b)}^{n - 2} b^{2}$ + ……………… + ⁿC_n_-1 $(a - b) b^{n - 1}$

=> $a^{n} - b^{n}$ = $(a - b)$ [ ${(a - b)}^{n - 1}$ + ⁿC₁ ${(a - b)}^{n - 2} b$ + ⁿC₂ ${(a - b)}^{n - 3} b^{2}$ +………..…… + ⁿC_n_-1 $b^{n - 1}$ ]

=> $a^{n} - b^{n}$ = $(a - b)$ k where k = [ ${(a - b)}^{n - 1}$ + ⁿC₁ ${(a - b)}^{n - 2} b$ + ⁿC₂ ${(a - b)}^{n - 3} b^{2}$ +………..…… + ⁿC_n_-1 $b^{n - 1}$ ] is a natural number.

Therefore (a – b) is a factor of aⁿ – bⁿwhere n is positive integer.

15. Find the expansion of (3x²– 2ax + 3a²)³using binomial theorem.

15. ${[3 x^{2} - 2 a x + 3 a^{2}]}^{3}$

= ${[3 x^{2} + a (- 2 x + 3 a)]}^{3}$

We know that by binomial theorem,

${(a + b)}^{3}$ = $a^{3} + b^{3} + 3 a b (a + b)$

= $a^{3} + b^{3} + 3 a^{2} b + 3 a b^{2}$

Then,

${[3 x^{2} + a (- 2 x + 3 a)]}^{3}$

= (3x²)³ + ${[a (- 2 x + 3 a)]}^{3}$ + $[3 (3 x^{2})^{2} a (- 2 x + 3 a)]$ + $[3 (3 x^{2}) {a (- 2 x + 3 a)}^{2}]$

= 27x⁶ + $[a^{3} {(- 2 x + 3 a)}^{3}]$ + $[3 (9 x^{4}) (- 2 a x + 3 a^{2})]$ + $[3 (3 x^{2}) {a^{2} {(3 a - 2 x)}^{2}}]$

= 27x⁶ + $[a^{3} {- 8 x^{3} + 27 a^{3} + 3 (4 x^{2}) (3 a) + 3 (- 2 x) (9 a^{2})}]$ + $[- 54 a x^{5} + 81 a^{2} x^{4}]$ + [ $(9 a^{2} x^{2})$ $(9 a^{2} + 4 x^{2} - 12 a x)$ ]

= 27x⁶ + [ $- 8 a^{3} x^{3} + 27 a^{6} + 36 a^{4} x^{2} - 54 a^{5} x$ ] + [ $- 54 a x^{5} + 81 a^{2} x^{4}$ ] + [ $(81 a^{4} x^{2} + 36 a^{2} x^{4} - 108 a^{3} x^{3}$ ]

= 27x⁶ $- 8 a^{3} x^{3} + 27 a^{6} + 36 a^{4} x^{2} - 54 a^{5} x$ $- 54 a x^{5} + 81 a^{2} x^{4}$ + $81 a^{4} x^{2} + 36 a^{2} x^{4} - 108 a^{3} x^{3}$

= 27x⁶– 54ax⁵ $+ 117 a^{2} x^{4}$ $- 116 a^{3} x^{3}$ + $117 a^{4} x^{2}$ $- 54 a^{5} x$ $+ 27 a^{6}$

Chapter 7 Binomial Theorem Exercise 7.2 Solutions

Binomial Theorem Exercise 7.2 focuses on the foundational concepts and delves into the application of binomial expansion. Exercise 7.2 of Binomial theorem focuses on the computation of specific terms in a binomial expansion, emphasizing the general term formula and finding a specific formula. Students can check below for binomial theorem ex 7.2 NCERT solutions;

Binomial Theorem Exercise 7.2 NCERT Solutions

Find the coefficient of

Q1. x⁵in (x + 3)⁸

A.1. Let x⁵ occurs in (r + 1)^th term of the expansion (x + 3)⁸.

Now, T_r₊₁ = ⁸C_r $. x^{8 - r} . 3^{r}$

Comparing indices of x in T_r₊₁ with x⁵ we get,

8 – r = 5

=>r = 8 – 5 = 3

So, Co-efficient of x⁵ is

⁸C₃× 3³

= $\frac{8!}{3! (8 - 3)!}$ × 27

= $\frac{8′ 7′ 6′ 5!}{3′ 2′ 1′ 5!}$ × 27

= 56 × 27

= 1512

Q2. a⁵b⁷in (a – 2b)¹².

A.2. Let a⁵b⁷ occurs in (r + 1)^th term of [removed]a – 2b)¹².

Now, T_r₊₁ = ¹²C_ra^12-r (–2b)^r

= (–1)^r¹²C_ra^12–r . 2^r. b^r

Comparing indices of a and b in T_r_-1 with a⁵ and b⁷ we get,

r = 7

So, co-efficient of a⁵b⁷ is (–1)⁷¹²C₇ 2⁷

= –1 × $\frac{12!}{7!' (12 - 7)!}$ × 2⁷

= –1 × $\frac{1 2′ 1 1′ 1 0′ 9′ 8′ 7!}{7!' 5!}$ × 128

= –1 × $\frac{1 2′ 1 1′ 1 0′ 9′ 8}{5′ 4′ 3′ 2′ 1}$ × 128

= –1 × 792 × 128

= – 101376

Write the general term in the expansion of

Q3. (x²–y)⁶

A.3. Let (r + 1)^th term be the general term of (x²–y)⁶.

So, T_r_-1 = ⁶C_r (x²)^6-r (-y)^r

= (–1)^r .⁶C_r . $x^{12 - r}$ . $y^{r}$

Q4. ( $x^{2} - y x)^{12}$ , x≠ 0.

A.4. Let (r + 1)th be the general term of ( $x^{2} - y x)^{12}$

So, T_r_-1 = ¹²C_r (x²)^12–r (–yx)^r

= (–1)^r¹²C_rx^24–2ry^rx^r

= (–1)^r¹²C_r $x^{24 - 2 r + r} y^{r}$

= (-1)^r¹²C_r $x^{24 - r} y^{r}$

Q5. Find the 4thterm in the expansion of (x – 2y)¹².

A.5. General term of the expansion ${(x - 2 y)}^{12}$ is given by

T_r₊₁ = ¹²C_r ${(x)}^{12 - r} {(- 2 y)}^{r}$

For 4th term, r + 1 = 4 i.e., r = 3

Therefore, T₄ = T₃₊₁ = ¹²C₃ ${(x)}^{12 - 3} {(- 2 y)}^{3}$

= $\frac{12!}{3! (12 - 3)!}$ $x^{9} {(- 1)}^{3} 2^{3} y^{3}$

= $- \frac{1 2′ 1 1′ 1 0′ 9!}{3′ 2′ 1′ 9!}$ ${(x)}^{9}$ × (8 $y)^{3}$

= – 220 x⁹× 8y³

= – 1760x⁹y³

Find the middle terms in the expansions of

Q6. ${(3 - \frac{x^{3}}{6})}^{7}$

A.6. As n = 7 is odd, the middle term are the ${(\frac{n + 1}{2})}^{t h}$ term and ${(\frac{n + 1}{2} + 1)}^{t h}$ term. i.e. ${(\frac{7 + 1}{2})}^{t h}$ and ${(\frac{7 + 1}{2} + 1)}^{t h}$ term which is 4^th term and 5^th term. i.e. T₄ and T₅.

Hence, T₄ = T₃₊₁ = ⁷C₃(3)^7-3 ${(- \frac{x^{3}}{6})}^{3}$

= $\frac{7!}{3! (7 - 3)!}$ × 3⁴ (–1)³ $(\frac{x^{3× 3}}{2^{3} . 3^{3}})$

= $- \frac{7′ 6′ 5′ 4!}{3′ 2′ 1′ 4!}$ × $\frac{3^{4}}{3^{3}}$ × $\frac{x^{9}}{2^{3}}$

= – 35 × $\frac{3 x^{9}}{8}$

= $- \frac{105 x^{9}}{8}$

T₅ = T₄₊₁ = ⁷C₄× (3)^7-4 ${(\frac{- x^{3}}{6})}^{4}$

= $\frac{7!}{4! (7 - 4)!}$ × $\frac{3^{3}' x^{12}}{2^{4}' 3^{4}}$

= $\frac{7′ 6′ 5′ 4!}{4!' 3!}$ × $\frac{x^{12}}{2^{4}' 3}$

= $\frac{7′ 6′ 5}{3′ 2′ 1}$ × $\frac{x^{12}}{1 6′ 3}$

= $\frac{35 x^{12}}{48}$

Q7. ${(\frac{x}{3} + 9 y)}^{10} .$

A.7. As n = 10 is even the middle term is ${(\frac{n}{2} + 1)}^{t h}$ i.e. ${(\frac{10}{2} + 1)}^{t h}$ term i.e. 6th term.

So, T₆ = T₅₊₁ = ¹⁰C₅ ${(\frac{x}{3})}^{10 - 5}$ (9y)⁵

= $\frac{10!}{5! (10 - 5)!}$ × $\frac{x^{5}}{3^{5}}$ × 3^5x2y⁵

= $\frac{1 0′ 9′ 8′ 7′ 6′ 5!}{5′ 4′ 3′ 2′ 1′ 5!}$ × 3⁵x⁵y⁵

= 2 × 9 × 2 × 7 × 243 x⁵y⁵

= 61236 x⁵y⁵

Q8. In the expansion of (1 + a)^m⁺ⁿ,prove that coefficients of anand anare equal.

A.8. The general term of the expansion (1 + a)^m⁺ⁿ is

T_r₊₁ = ^m⁺ⁿC_ra^r [since, 1^m^+n-r = 1]

At r = m we have,

T_m₊₁ = ^m⁺ⁿC_ma^m

= $\frac{(m + n)!}{m! (m + n - m)!}$ (a)^m

= $\frac{(m + n)!}{m! n!}$ a^m --------------- (1)

Similarly at r = n we have,

T_n₊₁ = ^m⁺ⁿC_naⁿ

= $\frac{(m + n)!}{n! (m + n - n)!}$ (a)ⁿ

= $\frac{(m + n)!}{n! m!}$ aⁿ --------------- (2)

Hence from (1) & (2),

Co-efficient of am = Co-efficient of aⁿ = $\frac{(m + n)!}{m! n!}$

Q9. The coefficients of the (r – 1)^th, r^thand (r + 1)^thterms in the expansion of (x + 1)ⁿ are in the ratio 1 : 3 : 5. Find n and r.

A.9. The general term of the expansion (x +1)ⁿ is

T_r₊₁ = ⁿC_rxⁿ^–r1^r

i.e. co-efficient of ${(r + 1)}^{t h}$ term = ⁿC_r

So, co-efficient of ${(r - 1)}^{t h}$ term =ⁿC_{(r–1) – 1} = ⁿC_r_{– 2}

Similarly, co-efficient of rth term = ⁿC_r_{– 1}

Given that, ⁿC_r_{– 2}:ⁿC_r_{– 1}: ⁿC_r = 1 : 3 : 5

We have,

= $\frac{1}{3}$

=> $\frac{n!}{(r - 2)! (n - r + 2)!}$ × $\frac{(r - 1)! (n - r + 1)!}{n!}$ = $\frac{1}{3}$

=> $\frac{(r - 1) (r - 2)! (n - r + 1)!}{(r - 2)! (n - r + 2) (n - r + 1)!}$ = $\frac{1}{3}$

=> $\frac{(r - 1)}{(n - r + 2)}$ = $\frac{1}{3}$

=> 3r – 3 = n – r + 2

=> 3r + r = n + 2 + 3

=> 4r = n + 5 -------------- (1)

And,

= $\frac{3}{5}$

=> $\frac{n!}{(r - 1)! (n - r + 1)!}$ × $\frac{r! (n - r)!}{n!}$ = $\frac{3}{5}$

=> $\frac{r (r - 1)! (n - r)!}{(r - 1)! (n - r + 1) (n - r)!}$ = $\frac{3}{5}$

=> $\frac{r}{n - r + 1}$ = $\frac{3}{5}$

=> 5r = 3n – 3r + 3

=> 5r + 3r = 3n + 3

=> 8r = 3n + 3 ----------------------- (2)

Multiplying equation (1) by 2 and subtracting from equation (2) we get,

8r – 8r = 3n + 3 – (2n + 10)

=> 0 = 3n + 3 – 2n – 10

=> 0 = n – 7

=>n = 7

Putting n = 7 in equation (1) we get,

=> 4r = 7 + 5

=>r = $\frac{12}{4}$

=>r = 3

Q10. Prove that the coefficient of xⁿin the expansion of (1 + x)²ⁿis twice the coefficientof xⁿin the expansion of (1 + x)^2n-1.

A.10. General term of the expansion (1 + x)²ⁿ is

T_r₊₁ = ²ⁿC_r (1)^2n-r(x)^r

So, co-efficient of xⁿ (i.e. r = n) is ²ⁿC_n

Similarly general term of the expansion (1 + x)^2n–1 is

T_r₊₁ = ^2n-1C_r (1)^2n–1–rx^r

And co-efficient of xⁿ i.e. when r = n is ^2n-1C_n

Therefore,

$\frac{c o - e f f i c i e n t o f x^{n} i n {(1 + x)}^{2 n}}{c o - e f f i c i e n t o f x^{n} i n {(1 + x)}^{2 n - 1}}$

= $\frac{2 n!}{n! (2 n - n)!}$ ÷ $\frac{(2 n - 1)!}{n! (2 n - 1 - n)!}$

= $\frac{2 n!}{n! n!}$ × $\frac{n! (n - 1)!}{(2 n - 1)!}$

= $\frac{2 n′ (2 - 1)!}{n!' n′ (n - 1)!}$ × $\frac{n! (n - 1)!}{(2 n - 1)!}$

= $\frac{2 n}{n}$

= 2

Thus, co-efficient of $x^{n}$ in ${(1 + x)}^{2 n}$ = 2x co-efficient of $x^{n}$ in ${(1 + x)}^{2 n - 1}$

Q.11. Find a positive value of m for which the coefficient of x²in the expansion (1 + x)^mis 6.

A.11. The general term of the expansion ${(1 + x)}^{m}$ is given by,

T_r₊₁ = ^mC_r $1^{m - r} x^{r}$

= ^mC_rx^r

At r = 2,

T₂₊₁ = ^mC₂x²

Given that, co-efficient of x² = 6

=>^mC₂ = 6

=> $\frac{m!}{2! (m - 2)!}$ = 6

=> $\frac{m′ (m - 1)' (m - 2)!}{2′ 1′ (m - 2)!}$ = 6

=> $\frac{m′ (m - 1)}{2}$ = 6

=>m² – m = 12

=>m² – m – 12 = 0

=>m² + 3m – 4m – 12 = 0

=>m(m + 3) – 4(m+ 3) = 0

=> (m – 4)(m + 3) = 0

=>m = 4 and m = –3

Since, we need a positive value of m we have,

m = 4

Chapter 7 Binomial Theorem Miscellaneous Exercise Solutions

Q1. Find a, b and n in the expansion of (a + b)ⁿ if the first three terms of the expansion are 729, 7290 and 30375, respectively.

A.1.The general term of the expansion (a + b)ⁿ is given by

T_r₊₁ = ⁿC_raⁿ^–rb^r

So, T₁ = ⁿC₀aⁿ = aⁿ

T₂ = ⁿC₁aⁿ^-1b = $\frac{n!}{1! (n - 1)!}$ aⁿ^-1 b = $\frac{n \times (n - 1)!}{(n - 1)!}$ aⁿ^-1b = naⁿ^-1b

T₃ = ⁿC₂aⁿ^-2b² = $\frac{n!}{2! (n - 2) [!}$ aⁿ^-2b² = $\frac{n \times (n - 1) \times (n - 2)!}{2 \times 1 \times (n - 2)!}$ aⁿ^-2b² = $\frac{n (n - 1)}{2}$ aⁿ^-2b²

Given,

T₁ = 729

=>aⁿ = 729 ------------------ (1)

T₂ = 7290

=>naⁿ^–1b = 7290 ------------- (2)

T₃ = 30375

=> $\frac{n (n - 1)}{2}$ aⁿ^–2b² = 30375 ------------------- (3)

Dividing equation (2) by (1) we get,

$\frac{n a^{n - 1} b}{a^{n}}$ = $\frac{7290}{729}$

=> $\frac{n b}{a}$ = 10

Similarly dividing equation (3) by (2) we get,

$\frac{n (n - 1)}{2}$ aⁿ^–2b² ÷ naⁿ^–1b = $\frac{30375}{7290}$

=> $\frac{n (n - 1)}{2}$ aⁿ^–2b²× $\frac{1}{n a^{n - 1} b}$ = $\frac{30375}{7290}$

=> $n (n - 1) a^{n - 2} b^{2}$ × $\frac{1}{n a^{n - 1} b}$ = $\frac{30375}{7290}$ × 2

=> $\frac{(n - 1) b}{a}$ = $\frac{2 5′ \times 2}{6}$

=> $\frac{n b}{a}$ $- \frac{b}{a}$ = $\frac{25}{3}$

=> 10 – $\frac{b}{a}$ = $\frac{25}{3}$ [since, $\frac{n b}{a}$ = 10]

=> $\frac{b}{a}$ = 10 – $\frac{25}{3}$

= $\frac{30 - 25}{3}$

= $\frac{5}{3}$ --------------- (5)

Putting equation (5) in (4) we get,

n× $\frac{5}{3}$ = 10

=>n = 10 × $\frac{3}{5}$

=>n = 6

So putting the value of n in equation (1) we get,

a6 = 729

=>a⁶= 36

=>a = 3

And putting a = 3 in equation (5) we get,

$\frac{b}{a}$ = $\frac{5}{3}$

=>b = $\frac{5}{3}$ ×a

= $\frac{5}{3}$ × 3

= 5

Q2. Find a if the coefficients of x²and x³in the expansion of (3 + ax)⁹are equal.

A.2. The general term of the expansion ${(3 + a x)}^{9}$ is

T_r₊₁ = ⁹C_r $3^{(9 - r)}$ ${(a x)}^{r}$

= ⁹C_r $3^{(9 - r)} a^{r} x^{r}$

At r = 2,

T₂₊₁ = ⁹C₂ $3^{(9 - 2)} a^{2} x^{2}$

= $\frac{9!}{2! (9 - 2)!}$ 3⁷a²x²

= $\frac{9′ 8′ 7!}{2′ 1′ 7!}$ 3⁷a²x²

= 36 ×3⁷a²x²

At r = 3,

T₃₊₁ = ⁹C₃ $3^{(9 - 3)} a^{3} x^{3}$

= $\frac{9!}{3! (9 - 3)!}$ 3⁶a³x³

= $\frac{9′ 8′ 7′ 6!}{3′ 2′ 1′ 6!}$ 3⁶a³x³

= 84 ×3⁶a³x³

Given that,

Co-efficient of $x^{2}$ = co-efficient of $x^{3}$

=> 36 × $3^{7} a^{2}$ = 84 × $3^{6} a^{3}$

=> $\frac{a^{3}}{a^{2}}$ = $\frac{3 6′ 3^{7}}{8 4′ 3^{6}}$

=> $a$ = $\frac{3′ 3}{7}$

= $\frac{9}{7}$

Q3. Find the coefficient of x5in the product (1 + 2x)⁶(1 – x)⁷using binomial theorem.

A.3. We first expand each of the factors of the given product using Binomial theorem. We have,

(1 + 2x)⁶= ⁶C₀ (1)⁶ + ⁶C₁ (1)⁵(2x) + ⁶C₂ (1)⁴(2x)² + ⁶C₃ (1)³(2x)³ + ⁶C₄ (1)²(2x)⁴ + ⁶C₅ (1)(2x)⁵ + ⁶C₆(2x)⁶

= $[\frac{6!}{0! (6 - 0)!}' 1]$ + $[\frac{6!}{1! (6 - 1)!}' 1' (2 x)]$ + $[\frac{6!}{2! (6 - 2)!}' 1' 4 x^{2}]$ + $[\frac{6!}{3! (6 - 3)!}' 1' 8 x^{3}]$ + $[\frac{6!}{4! (6 - 4)!}' 1' 16 x^{4}]$ + $[\frac{6!}{5! (6 - 5)!}' 1' 32 x^{5}]$ + $[\frac{6!}{6! (6 - 6)!}' 64 x^{6}]$

= [1] + $[\frac{6′ 5!}{1′ 5!}' (2 x)]$ + $[\frac{6′ 5′ 4!}{2′ 1′ 4!}' 4 x^{2}]$ + $[\frac{6′ 5′ 4′ 3!}{3′ 2′ 1′ 3!}' (8 x^{3})]$ + $[\frac{6′ 5′ 4!}{4!' 2!}' 16 x^{4}]$ + $[\frac{6′ 5!}{5!' 1!}' (32 x^{5})]$ + [1 ×64x6]

= 1 + 12 $x$ + 60x² + 160x³ + 240x⁴ + 192x⁵ + 64x⁶

And,

(1 – x)⁷= ⁷C₀ (1)⁷ + ⁷C₁ (1)⁶(–x) + ⁷C₂ (1)⁵(–x)² + ⁷C₃ (1)⁴(–x)³ + ⁷C₄ (1)³(–x)⁴ + ⁷C₅ (1)²(–x)⁵ + ⁷C₆ (1) (–x)⁶ + ⁷C₇(–x)⁷

= $[\frac{7!}{0! (7 - 0)!}' 1]$ + $[\frac{7!}{1! (7 - 1)!}' 1' (- x)]$ + $[\frac{7!}{2! (7 - 2)!}' 1' x^{2}]$ + $[\frac{7!}{3! (7 - 3)!}' 1' {(- x)}^{}]$ + $[\frac{7!}{4! (7 - 4)!}' 1' x^{4}]$ + $[\frac{7!}{5! (7 - 5)!}' 1' {(- x)}^{5}]$ + $[\frac{7!}{6! (7 - 6)!}' 1' x^{6}]$ + [ $[\frac{7!}{7! (7 - 7)!}' {(- x)}^{7}]$

= [1] + $[\frac{7′ 6!}{1′ 6!}' (- x)]$ + $[\frac{7′ 6′ 5!}{2′ 1′ 5!}' x^{2}]$ + $[\frac{7′ 6′ 5′ 4!}{3′ 2′ 1′ 4!}' (- x^{3})]$ + $[\frac{7′ 6′ 5′ 4!}{4!' 3!}' x^{4}]$ + $[\frac{7′ 6′ 5!}{5!' 2!}' (- x^{5})]$ + $[\frac{7′ 6!}{6!' 1!}' x^{6}]$ + [1 ×(–x)7]

= 1 – 7x + 21x² – 35x³ + 35x⁴– 21x⁵ + 7x⁶– x⁷

Thus, ${(1 + 2 x)}^{6} {(1 - x)}^{7}$

= (1 + 12x + 60x² + 160x³ + 240x⁴ + 192x⁵ + 64x⁶)( 1 – 7x + 21x² – 35x³ + 35x⁴– 21x⁵ + 7x⁶– x⁷)

We need to find only the term involving x⁵ i.e. x^rx^{5 – r}

The terms with x⁵ are

= (1)(–21x⁵) + (12x)(35x⁴) + (60x²)(–35x³) + (160x³)(21x²) + (240x⁴)(–7x) + (192x⁵)(1)

= –21x⁵ + 420x⁵– 2100x⁵ + 3360x⁵– 1680x⁵ + 192x⁵

= 3972x⁵– 3801x⁵

= 171x⁵

Hence, co-efficient of x⁵ is 171.

Q4. If a and b are distinct integers, prove that a – b is a factor of aⁿ– bⁿ, whenever n is a positive integer.

[Hint: write aⁿ= (a – b + b)n and expand]

A.4. For (a – b) to be a factor of aⁿ – b ⁿwe need to show (aⁿ – bⁿ) = (a – b)k as k is a natural number.

We have, for positive n

aⁿ = ${(a - b + b)}^{n}$ = ${[(a - b) + b]}^{n}$

=>aⁿ = ⁿC₀(a – b)ⁿ + ⁿC₁(a – b)^{n -}¹b + ⁿC₂(a – b)^{n –}²b² + ………… +ⁿC_n_-1 $(a - b) b^{n - 1}$ + ⁿC_nbⁿ

=>aⁿ= ${(a - b)}^{n}$ + ⁿC₁ ${(a - b)}^{n - 1} b$ + ⁿC₂ ${(a - b)}^{n - 2} b^{2}$ + …………….…+ ⁿC_n_-1 $(a - b) b^{n - 1}$ + $b^{n}$ [Since, ⁿC₀ = 1 and ⁿC_n = 1]

=> $a^{n} - b^{n}$ = ${(a - b)}^{n}$ +ⁿC₁ ${(a - b)}^{n - 1} b$ + ⁿC₂ ${(a - b)}^{n - 2} b^{2}$ + ……………… + ⁿC_n_-1 $(a - b) b^{n - 1}$

=> $a^{n} - b^{n}$ = $(a - b)$ [ ${(a - b)}^{n - 1}$ + ⁿC₁ ${(a - b)}^{n - 2} b$ + ⁿC₂ ${(a - b)}^{n - 3} b^{2}$ +………..…… + ⁿC_n_-1 $b^{n - 1}$ ]

=> $a^{n} - b^{n}$ = $(a - b)$ k where k = [ ${(a - b)}^{n - 1}$ + ⁿC₁ ${(a - b)}^{n - 2} b$ + ⁿC₂ ${(a - b)}^{n - 3} b^{2}$ +………..…… + ⁿC_n_-1 $b^{n - 1}$ ] is a natural number.

Therefore (a – b) is a factor of aⁿ – bⁿwhere n is positive integer.

Q5. Find an approximation of (0.99)⁵using the first three terms of its expansion.

A.5. (0.99)⁵ = (1 – 0.01)⁵

By binomial theorem expanding upto first three terms, we get

(1 – 0.01)⁵ = ⁵C₀ (1)⁵ + ⁵C₁ (1)⁴(-0.01) + ⁵C₂ (1)³(-0.01)²

= $(\frac{5!}{0! (5 - 0)!}' 1)$ + $[\frac{5!}{1! (5 - 1)!}' 1' (- 0.01)]$ + $(\frac{5!}{2! (5 - 2)!}' 1' 0.0001)$

= (1 × 1) – $(\frac{5′ 4!}{1′ 4!}' 1' 0.01)$ + $(\frac{5′ 4′ 3!}{2′ 1′ 3!}' 1' 0.0001)$

= 1 – 0.05 + 0.001

= 1.001 – 0.05

= 0.951

Q6. Expand using Binomial Theorem ${(1 + \frac{x}{2} - \frac{2}{x})}^{4}, x \neq 0 .$

A.6. ${(1 + \frac{x}{2} - \frac{2}{x})}^{4}$

Using binomial theorem we have,

${[(1 + \frac{x}{2}) - \frac{2}{x}]}^{4}$

= ⁴C₀ ${(1 + \frac{x}{2})}^{4}$ + ⁴C₁ ${(1 + \frac{x}{2})}^{3} (- \frac{2}{x})$ + ⁴C₂ ${(1 + \frac{x}{2})}^{2} {(- \frac{2}{x})}^{2}$ + ⁴C₃ $(1 + \frac{x}{2}) {(- \frac{2}{x})}^{3}$ + ⁴C₄ ${(- \frac{2}{x})}^{4}$

= $[\frac{4!}{0! (4 - 0)!} {(1 + \frac{x}{2})}^{4}]$ – $[\frac{4!}{1! (4 - 1)!} {(1 + \frac{x}{2})}^{3} (\frac{2}{x})]$ + $[\frac{4!}{2! (4 - 2)!} {(1 + \frac{x}{2})}^{2} (\frac{4}{x^{2}})]$ – $[\frac{4!}{3! (4 - 3)!} (1 + \frac{x}{2}) (\frac{8}{x^{3}})]$ + $[\frac{4!}{4! (4 - 4)!} (\frac{16}{x^{4}})]$

= $1′ {(1 + \frac{x}{2})}^{4}$ – $[{(1 + \frac{x}{2})}^{3} (\frac{2}{x})]$ + $[\frac{4′ 3′ 2!}{2′ 1′ 2!} {(1 + \frac{x}{2})}^{2} (\frac{4}{x^{2}})]$ – $[\frac{43!}{3! 1!} (1 + \frac{x}{2}) (\frac{8}{x^{3}})]$ + $[1′ (\frac{16}{x^{4}})]$

= ${(1 + \frac{x}{2})}^{4}$ – 4 $[{(1 + \frac{x}{2})}^{3} (\frac{2}{x})]$ + 6 $[{(1 + \frac{x}{2})}^{2} (\frac{4}{x^{2}})]$ – 4 $[(1 + \frac{x}{2}) (\frac{8}{x^{3}})]$ + $(\frac{16}{x^{4}})$ ----- (1)

Now,

${(1 + \frac{x}{2})}^{4}$

= ⁴C₀(1)⁴ + ⁴C₁ (1)³ $(\frac{x}{2})$ + ⁴C₂(1)² ${(\frac{x}{2})}^{2}$ + ⁴C₃(1) ${(\frac{x}{2})}^{3}$ + C₄ ${(\frac{x}{2})}^{4}$

= $(\frac{4!}{0! (4 - 0)!}' 1)$ + $(\frac{4!}{1! (4 - 1)!}' 1′ \frac{x}{2})$ + $(\frac{4!}{2! (4 - 2)!}' 1′ \frac{x^{2}}{4})$ + $(\frac{4!}{3! (4 - 3)!}' 1′ \frac{x^{3}}{8})$ + $(\frac{4!}{4! (4 - 4)!}' 1′ \frac{x^{4}}{16})$

= 1 + $(\frac{4′ 3!}{1′ 3!}' \frac{x}{2})$ + $(\frac{4′ 3′ 2!}{2′ 1′ 2!}' \frac{x^{2}}{4})$ + $(\frac{4′ 3!}{3! 1!}' \frac{x^{3}}{8})$ + $(1′ \frac{x^{4}}{16})$

= 1 + 2x + $\frac{3 x^{2}}{2}$ + $\frac{x^{3}}{2}$ + $\frac{x^{4}}{16}$ ------------------- (2)

${(1 + \frac{x}{2})}^{3}$

= ³C₀(1)³ + ³C₁ (1)² $(\frac{x}{2})$ +³C₂ (1) ${(\frac{x}{2})}^{2}$ + ³C₃ ${(\frac{x}{2})}^{3}$

= $(\frac{3!}{0! (3 - 0)!}' 1)$ + $(\frac{3!}{1! (3 - 1)!}' 1′ \frac{x}{2})$ + $(\frac{3!}{2! (3 - 2)!}' 1′ \frac{x^{2}}{4})$ + $(\frac{3!}{3! (3 - 3)!}' 1′ \frac{x^{3}}{8})$

= 1 + $(\frac{3′ 2!}{1′ 2!}' \frac{x}{2})$ + $(\frac{3′ 2!}{2! 1!}' \frac{x^{2}}{4})$ + $(1′ \frac{x^{3}}{8})$

= 1 + $\frac{3 x}{2}$ + $\frac{3 x^{2}}{4}$ + $\frac{x^{3}}{8}$ ------------------------ (3)

And, ${(1 + \frac{x}{2})}^{2}$

= ²C₀(1)² + ²C₁ (1) $(\frac{x}{2})$ + ²C₂ ${(\frac{x}{2})}^{2}$

= $(\frac{2!}{0! (2 - 0)!}' 1)$ + $(\frac{2!}{1! (2 - 1)!}' 1′ \frac{x}{2})$ + $(\frac{2!}{2! (2 - 2)!}' \frac{x 2}{4})$

= 1 + $(\frac{2′ 1}{1′ 1!}' 1′ \frac{x}{2})$ + $\frac{x^{2}}{4}$

= 1 + x + $\frac{x^{2}}{4}$ ---------------------------- (4)

Putting (2), (3) and (4) in (1) we get,

${(1 + \frac{x}{2} - \frac{2}{x})}^{4}$

= 1 + 2x + $\frac{3 x^{2}}{2}$ + $\frac{x^{3}}{2}$ + $\frac{x^{4}}{16}$ – 4 $[(1 + \frac{3 x}{2} + \frac{3 x^{2}}{2} + \frac{x^{3}}{2}) (\frac{2}{x})]$ + 6 $[(1 + x + \frac{x^{2}}{4}) (\frac{4}{x^{2}})]$ – 4 $[(1 + \frac{x}{2}) (\frac{8}{x^{3}})]$ + $(\frac{16}{x^{4}})$

= 1 + 2x + $\frac{3 x^{2}}{2}$ + $\frac{x^{3}}{2}$ + $\frac{x^{4}}{16}$ – $\frac{8}{x}$ – 12 – 6x –x² + $\frac{24}{x^{2}}$ + $\frac{24}{x}$ + 6 – $\frac{32}{x^{3}}$ – $\frac{16}{x^{2}}$ + $\frac{16}{x^{4}}$

= $\frac{16}{x}$ + $\frac{8}{x^{2}}$ – $\frac{32}{x^{3}}$ + $\frac{16}{x^{4}}$ – 4x+ $\frac{x^{2}}{2}$ + $\frac{x^{3}}{2}$ + $\frac{x^{4}}{16}$ – 5

Q7. Find the expansion of (3x²– 2ax + 3a²)³using binomial theorem.

A.7. ${[3 x^{2} - 2 a x + 3 a^{2}]}^{3}$

= ${[3 x^{2} + a (- 2 x + 3 a)]}^{3}$

We know that by binomial theorem,

${(a + b)}^{3}$ = $a^{3} + b^{3} + 3 a b (a + b)$

= $a^{3} + b^{3} + 3 a^{2} b + 3 a b^{2}$

Then,

${[3 x^{2} + a (- 2 x + 3 a)]}^{3}$

= (3x²)³ + ${[a (- 2 x + 3 a)]}^{3}$ + $[3 (3 x^{2})^{2} a (- 2 x + 3 a)]$ + $[3 (3 x^{2}) {a (- 2 x + 3 a)}^{2}]$

= 27x⁶ + $[a^{3} {(- 2 x + 3 a)}^{3}]$ + $[3 (9 x^{4}) (- 2 a x + 3 a^{2})]$ + $[3 (3 x^{2}) {a^{2} {(3 a - 2 x)}^{2}}]$

= 27x⁶ + $[a^{3} {- 8 x^{3} + 27 a^{3} + 3 (4 x^{2}) (3 a) + 3 (- 2 x) (9 a^{2})}]$ + $[- 54 a x^{5} + 81 a^{2} x^{4}]$ + [ $(9 a^{2} x^{2})$ $(9 a^{2} + 4 x^{2} - 12 a x)$ ]

= 27x⁶ + [ $- 8 a^{3} x^{3} + 27 a^{6} + 36 a^{4} x^{2} - 54 a^{5} x$ ] + [ $- 54 a x^{5} + 81 a^{2} x^{4}$ ] + [ $(81 a^{4} x^{2} + 36 a^{2} x^{4} - 108 a^{3} x^{3}$ ]

= 27x⁶ $- 8 a^{3} x^{3} + 27 a^{6} + 36 a^{4} x^{2} - 54 a^{5} x$ $- 54 a x^{5} + 81 a^{2} x^{4}$ + $81 a^{4} x^{2} + 36 a^{2} x^{4} - 108 a^{3} x^{3}$

= 27x⁶– 54ax⁵ $+ 117 a^{2} x^{4}$ $- 116 a^{3} x^{3}$ + $117 a^{4} x^{2}$ $- 54 a^{5} x$ $+ 27 a^{6}$

Binomial Theorem - FAQs

The following are the FAQs from the Binomial Theorem Class Maths:

Commonly asked questions

What is Binomial Theorem in Class 11 Maths?

An expression with two terms raised to a positive integer power can be expanded in Maths, such as (a + b)? This algebraic rule is known as the Binomial Theorem.

What is the binomial theorem class 11 formula?

Mathematically, binomial theorem formula is: (a + b)n = nC0 an + nC1 an - 1b + nC2 a n – 2b 2 + . + nCn – 1a.bn - 1 + nCn bn. Here a and b are real numbers and n is a positive integer.

What is the total number of exercises in binomial theorem class 11?

There are a total of 36 questions comprising 14 straightforward formula-based sums, 16 challenging problems, and 6 intermediate.

Which is the another name of the binomial model.

The Binomial model is known as the Lattice Model or Binomial Option Pricing Model.

Which are the common mistakes by students in binomial theorem class 11?

The common mistakes can be - using the formula incorrectly, before applying the formula students not simplify the expression, in Binomial Expansion, sometimes they forget to include the fractional and negative exponents, and using incorrect values for a, b, and n.

Explore exams which ask questions on Maths Ncert Solutions class 11th

Select your preferred stream

MBA

Engineering

Boards

View more exams

Maths Ncert Solutions class 11th Exam

Student Forum

Anything you would want to ask experts?

Write here...

Other Similar chapters for you

Popular Courses After 12th

ScienceCommerceArts

Bachelor of Technology (BE/BTech)
Exams accepted
JEE Main | BITSAT | WBJEE
Bachelor of Architecture (BArch)
Exams accepted
NATA | AAT | ITM NEST
Bachelor of Science (BSc)
Exams accepted
CUET | UPCATET | IIT JAM
Bachelor of Computer Applications (BCA)
Exams accepted
BUMAT | GSAT | SET
Bachelor of Medicine & Bachelor of Surgery (MBBS)
Exams accepted
NEET | AYUSH | FMGE

View all courses after 12th

Chartered Accountancy (CA)
Exams accepted
CA Foundation
Company Secretary (CS)
Exams accepted
ICSI Exam
BCom in Accounting & Commerce
Exams accepted
BHU UET | GLAET | GD Goenka Test
Bachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBE
BBA/BMS
Exams accepted
IPMAT | NMIMS - NPAT | SET

View all courses after 12th

BA in Humanities & Social Sciences
Exams accepted
SUAT | JNUEE | BHU UET
Bachelor of Fine Arts (BFA)
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance Exam
Bachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance Exam
BA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT India
Bachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test

View all courses after 12th

News & Updates

Latest NewsPopular News

Class 11 Maths Ch 7 Binomial Theorem NCERT Solutions | Step-by-Step Guide

Overview of Binomial Theorem – Class 11 Maths Chapter 7

Chapter 7 Binomial Theorem : Key Topics, Weightage

Chapter 7 Class 11 Maths Binomial Theorem Weightage in JEE Mains exam

Try these practice questions

Important Formulas of Ch 7 Maths Class 11 Binomial Theorem

Important Terms and Formulae for Binomial Theorem

4. Sum of Binomial Coefficients

5. Approximation Formula (for small $x$ )

Chapter 7 Binomial Theorem NCERT Solution PDF: Download PDF for Free

Related Links

Chapter 7 Binomial Theorem Exercise-wise Solution

Chapter 7 Binomial Theorem Exercise 7.1 Solutions

Binomial Theorem Exercise 7.1 NCERT Solutions

Commonly asked questions

Chapter 7 Binomial Theorem Exercise 7.2 Solutions

Binomial Theorem Exercise 7.2 NCERT Solutions

Chapter 7 Binomial Theorem Miscellaneous Exercise Solutions

Binomial Theorem - FAQs

Commonly asked questions

Explore exams which ask questions on Maths Ncert Solutions class 11th

Student Forum

Other Similar chapters for you

Popular Courses After 12th

News & Updates

UPPSC PCS Prelims Exam Analysis 2025 Live: Answer Key, Expected Cutoff

GATE 2026 Late Fee Registration Date Extended Live: Apply Now, Steps, Application Scrutiny, & Status

SSC Stenographer 2025 Result (Link Soon) @ssc.gov.in Live: Download Result & Cutoff PDF Here

IIT JAM Registration 2026 (Ending Soon) @jam2026.iitb.ac.in Live Updates; Steps to Apply, Eligibility, Fees

HBSE Date Sheet 2026 Class 12, 10 @bseh.org Live Updates

JEE Main Marks vs Percentile vs Rank 2025: Calculate Percentile and Rank Using Marks

List of NIT Colleges in India 2025 - NIRF Ranking, Courses, Seats, Cutoff, Fees and Placement

CBSE 10th Maths Question Paper 2025, 2024, 2023, 2022, 2020, 2019 PDF Download

NEET Chapter Wise Weightage 2026 PDF by NTA: Physics, Chemistry & Biology

List of Top IITs in India 2025: NIRF Ranking, Courses, Seats, Fees & Placement

Class 11 Maths Ch 7 Binomial Theorem NCERT Solutions | Step-by-Step Guide

Overview of Binomial Theorem – Class 11 Maths Chapter 7

Chapter 7 Binomial Theorem : Key Topics, Weightage

Chapter 7 Class 11 Maths Binomial Theorem Weightage in JEE Mains exam

Try these practice questions

Important Formulas of Ch 7 Maths Class 11 Binomial Theorem

Important Terms and Formulae for Binomial Theorem

4. Sum of Binomial Coefficients

5. Approximation Formula (for small x x x)

Chapter 7 Binomial Theorem NCERT Solution PDF: Download PDF for Free

Related Links

Chapter 7 Binomial Theorem Exercise-wise Solution

Chapter 7 Binomial Theorem Exercise 7.1 Solutions

Binomial Theorem Exercise 7.1 NCERT Solutions

Commonly asked questions

Chapter 7 Binomial Theorem Exercise 7.2 Solutions

Binomial Theorem Exercise 7.2 NCERT Solutions

Chapter 7 Binomial Theorem Miscellaneous Exercise Solutions

Binomial Theorem - FAQs

Commonly asked questions

Explore exams which ask questions on Maths Ncert Solutions class 11th

Student Forum

Other Similar chapters for you

Popular Courses After 12th

News & Updates

5. Approximation Formula (for small $x$ )