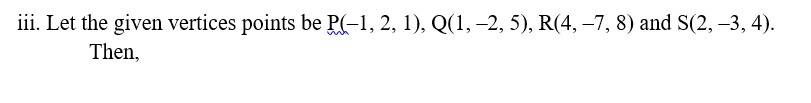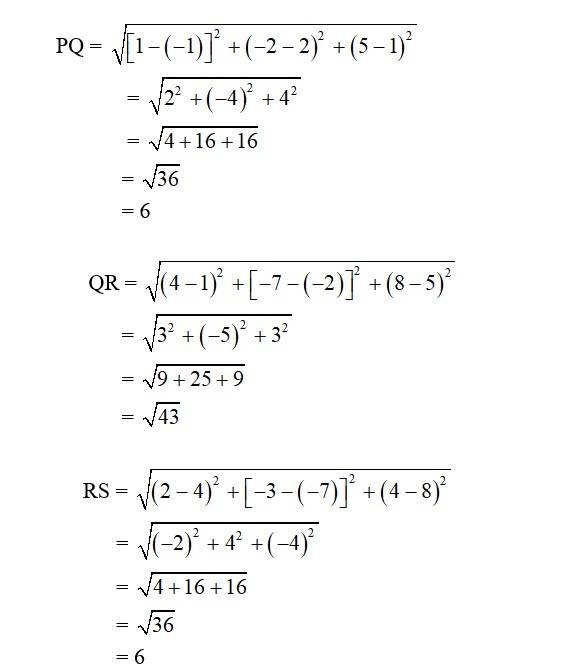Introduction to 3 Dimensional Geometry Class 11 chapter states that a point in space has three coordinates. The concepts are useful in situations where an electric bulb is hanging from the ceiling of a room, and we need to locate the position of the lowest tip of the bulb or the position of the central tip of the ceiling fan. We also need the height of the point from the floor of the room, along with the perpendicular distances of the point to be located from two perpendicular walls.
The key topics covered in the Introduction to 3d Geometry Class 11 include - coordinates of a point in space, distance between two points, and coordinate axes and coordinate planes in the 3D space. The coordinates of a point are the three numbers representing the perpendicular distances of the point.
Students who are looking for comprehensive chapter-wise NCERT notes of Class 11 Maths with important topics and solved examples can Explore Here. The notes are according to the latest CBSE 2025–26 syllabus hence ideal for the CBSE Board examination preparation.
- Highlights of Class 11 Maths Chapter 11: 3D Geometry
- Class 11 Math Chapter Introduction to Three Dimensional Geometry: Key Topics, Weightage
- Important Formulas of Introduction to 3d Geometry Class 11
- Class 11 Math Three Dimensional Geometry NCERT Solution PDF: Download Free PDF
- Class 11 Math Introduction to Three Dimensional Geometry Exercise-wise Solutions
- Class 11 Math Introduction to Three Dimensional Geometry Exercise 12.1 Solution
- Class 11 Math Introduction to Three Dimensional Geometry Exercise 12.2 Solution
- Class 11 Math Introduction to Three Dimensional Geometry Exercise 12.3 Solution
- Class 11 Math Introduction to Three Dimensional Geometry Miscellaneous Exercise Solution
Highlights of Class 11 Maths Chapter 11: 3D Geometry
Here is an overview of the introduction to three dimensional geometry class 11:
- The Class 11 Maths chapter 11 states that in a 3D rectangular Cartesian coordinate system, the coordinate axes are the three mutually perpendicular lines represented by x, y, and z axes.
- The three coordinate planes are determined by the pair of axes called the XY, YZ, and ZX - planes.
- It covers octants, which are the space divided into eight parts by the three coordinate planes.
- In three-dimensional geometry, the coordinates of a plane P are written in the form of a triplet like (x, y, z). The x,y,z are distances from the three planes - YZ, ZX, and XY-planes.(x, 0, 0) represents any point on x-axis, (0,y,0) represents point on y-axis, and (0, 0, z) represents a point on z-axis.
- The mathematical formula to show the difference between two points P(x1, y1, z1) and Q (x2, y2, z2) is given by:
Check here for the quick revision notes of NCERT Class 11 Physics, Chemistry & Maths. It will help you in developing the concept clarity.
Class 11 Math Chapter Introduction to Three Dimensional Geometry: Key Topics, Weightage
While preparing for the Class 11 introduction to 3d geometry, students must focus on distance and section formulas, understanding coordinate systems, and the representation of points in 3D space. See below the topics covered in the Class 11 introduction to 3 dimensional geometry:
| Exercise | Topics Covered |
|---|---|
| 11.1 | Introduction |
| 11.2 | Coordinate Axes and Coordinate Planes in Three Dimensional Space |
| 11.3 | Coordinates of a Point in Space |
| 11.4 | Distance between Two Points |
Introduction to 3 Dimensional Geometry Class 11 Weightage in JEE Mains
| Exam | Number of Questions | Weightage |
|---|---|---|
| JEE Mains | 2 questions | 6.6% to 8% |
Related Links
| NCERT Solutions Class 11 and 12 for Maths, Physics, Chemistry | NCERT Notes for Class 11 & 12 | NCERT Solutions for Class 11 Maths |
Important Formulas of Introduction to 3d Geometry Class 11
Important Formulae for Three-Dimensional Geometry
-
Distance Formula:
-
Section Formula (Dividing a Line Segment in Ratio )
-
Midpoint Formula:
-
Direction Cosines ( ) of a Line Passing Through the Origin:
-
Sum of the Squares of Direction Cosines:
Class 11 Math Three Dimensional Geometry NCERT Solution PDF: Download Free PDF
It is recommended for Class 11 Science students to download the free PDF of 3D Geometry Class 11 from the link given below. Once the student downloads the PDF, they can access it from anywhere, even without an internet connection. It is an effective study material for the students preparing for Class 11 exams, CBSE Board, and entrance exams like JEE Mains.
Class 11 Math 3D Geometry NCERT Solution PDF: Download PDF for Free
Class 11 Math Introduction to Three Dimensional Geometry Exercise-wise Solutions
Class 11 Math Three Dimensional Geometry focuses on introducing all basic concepts of 3D geometry to students. Introduction to Three-Dimensional Geometry Class 11 Math introduces students to various concepts such as the Representation of points in 3D space, the Distance between two points, and Section and midpoint formulas, Direction cosines and direction ratios. Students can check the solution of all the exercises of three-dimensional geometry chapter of class 11 mathematics below;
Class 11 Math Introduction to Three Dimensional Geometry Exercise 12.1 Solution
Class 11 Math Three-dimensional geometry Exercise 11.1 focuses on the fundamental concepts of three-dimensional coordinate geometry. There are a few fundamental concepts covered in this exercise. Key concepts covered in 3D Geometry Exercise 11.1: basics of 3D coordinate system (x-axis, y-axis, z-axis), and finding the distance between two points in 3D using the distance formula. Exercise 11.1 consists of 4 questions; solutions are available below for all the questions. Students can check the solution below.
Class 11 Math Three Dimensional Geometry Exercise 11.1 NCERT SolutionQ1. A point is on the x-axis. What are its y-coordinate and z-coordinates? |
| A.1. When a point lies on x-axis, its y-coordinate and z-coordinate are zero. |
| Q2. A point is in the XZ-plane. What can you say about its y-coordinate? |
| A.2. When a point lies on XZ-plane, its y-coordinate is zero. |
| Q3. Name the octants in which the following points lie: (1, 2, 3), (4, –2, 3), (4, –2, –5), (4, 2, –5), (– 4, 2, –5), (– 4, 2, 5), (–3, –1, 6) (– 2, – 4, –7). |
||||||||||||||||||||||||||||||||||||||||||||||||
| A.3.
(1, 2, 3) lies in octant I. (4, –2, 3) lies in octant IV. (4, –2, –5) lies in octant VIII. (4, 2, –5) lies in octant V. (–4, 2, –5) lies in octant VI. (–4, 2, 5) lies in octant II. (–3, –1, 6) lies in octant III. (–2, –4, –7) lies in octant VII. |
||||||||||||||||||||||||||||||||||||||||||||||||
| Q4. Fill in the blanks: The x-axis and y-axis taken together determine a plane known as_______. The coordinates of points in the XY-plane are of the form _______. Coordinate planes divide the space into ______ octants. |
| A.4. i. The x-axis and y-axis taken together determine a plane known as XY plane. ii. The coordinates of points in the XY-plane are of the form (x, y, 0). iii. Coordinate planes divide the space into 8 (eight) octants. |
Commonly asked questions
16. Find the lengths of the medians of the triangle with vertices A (0, 0, 6), B (0,4, 0) and (6, 0, 0).
16. In a triangle ABC, the medians are the line segment that joins a vertex to the mid-point of the side that is opposite to that vertex. So, AE, BF and CG are the three medians.
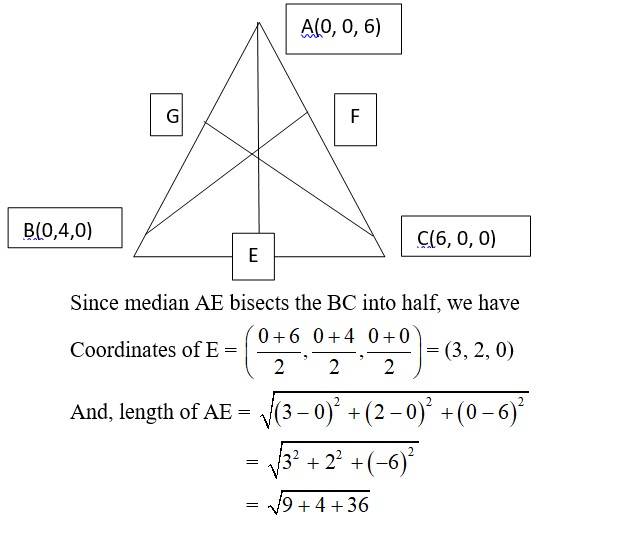

9. Find the equation of the set of points P, the sum of whose distances from A (4, 0, 0) and B (– 4, 0, 0) is equal to 10.
9. Let P have the co-ordinates (x, y, z).
Given that,
PA + PB = 10
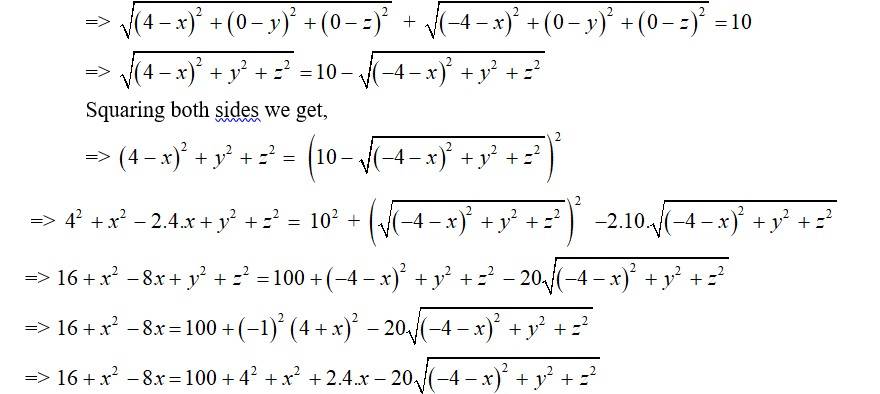


8. Find the equation of the set of points which are equidistant from the points (1, 2, 3) and (3, 2, –1).
8. Let P(x, y, z) be the point equidistant from the given points (1, 2, 3) say A and (3, 2, –1) say B.
So, PA = PB
=> =
Squaring both sides,
=> =
=>
=>
=>
=>
=>
=>
Therefore, the required equation of point is
4. Fill in the blanks:
(i) The x-axis and y-axis taken together determine a plane known as_______.
(ii) The coordinates of points in the XY-plane are of the form _______.
(iii) Coordinate planes divide the space into ______ octants.
4. i. The x-axis and y-axis taken together determine a plane known as XY plane.
ii. The coordinates of points in the XY-plane are of the form (x, y, 0).
iii. Coordinate planes divide the space into 8 (eight) octants.
12. Find the ratio in which the YZ-plane divides the line segment formed by joining the points (–2, 4, 7) and (3, –5, 8)
12. Let YZ-plane divides the line segment joining A (–2, 4, 7) and B (3, –5, 8) at point P (x, y, z) in the ratio k : 1.
Then the co-ordinates of P are.
As P lies on YZ-plane its x-coordinate is zero.
i.e.
=>
=>
Hence the YZ-plane divides AB internally in ratio.
: 1 = 2 : 3
20. If A and B be the points (3, 4, 5) and (–1, 3, –7), respectively, find the equation of the set of points P such that PA2 + PB2 = k2, where k is a constant.
20. Let P have the coordinates (x, y, z)
Then,

=
=
=
=
And,
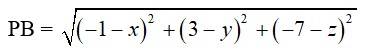
=> =
=
=
=
=
The equation of P such that,
=> +
=>
=>
=> =
2. A point is in the XZ-plane. What can you say about its y-coordinate?
2. When a point lies on XZ-plane, its y-coordinate is zero.
3. Name the octants in which the following points lie:
(1, 2, 3), (4, –2, 3), (4, –2, –5), (4, 2, –5), (– 4, 2, –5), (– 4, 2, 5), (–3, –1, 6) (– 2, – 4, –7).
3.
| Octants | |||||||
| I | II | III | IV | V | VI | VII | VIII |
coordinates | x | + | – | + | – | + | ||
y | + | – | + | – | – | |||
z | + | – | – | |||||
(1, 2, 3) lies in octant I.
(4, –2, 3) lies in octant IV.
(4, –2, –5) lies in octant VIII.
(4, 2, –5) lies in octant V.
(–4, 2, –5) lies in octant VI.
(–4, 2, 5) lies in octant II.
(–3, –1, 6) lies in octant III.
(–2, –4, –7) lies in octant VII.
Class 11 Math Three Dimensional Geometry Exercise 11.2 NCERT Solution
5. Find the distance between the following pairs of points:
(i) (2, 3, 5) and (4, 3, 1)
(ii) (–3, 7, 2) and (2, 4, –1)
(iii) (–1, 3, – 4) and (1, –3, 4)
(iv) (2, –1, 3) and (–2, 1, 3).
5. i. The distance between points (2, 3, 5) and (4, 3, 1) is
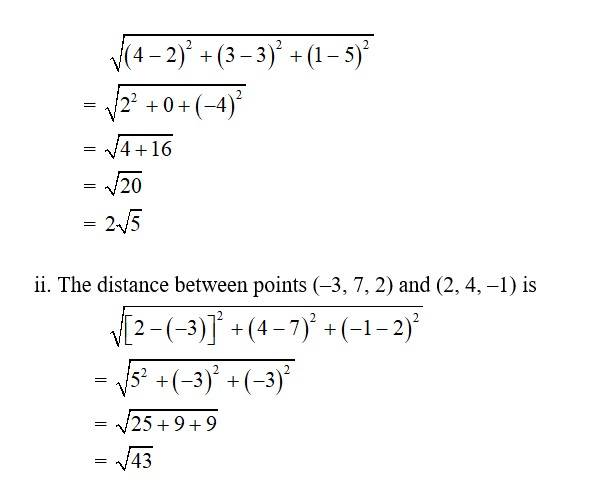

14. Find the coordinates of the points which trisect the line segment joining the points P (4, 2, – 6) and Q (10, –16, 6).
14. Let A(x1, y1, z1) and B(x2, y2, z2) trisect the line segment joining the points P(4, 2, –6) and Q(10, –16, 6).
Since A divides PQ internally in ratio 1 : 2. Then co-ordinates of A
=
=
=
= (6, –4, –2)
Similarly B divides PQ internally in ratio 2 : 1. Then co-ordinates of B
=
=
=
= (8, –10, 2)
Hence the points which trisects the line segment joining the points P(4, 2, –6) and Q(10, –16, 6) are (6, –4, –2) and (8, –1)
15. Three vertices of a parallelogram ABCD are A(3, – 1, 2), B (1, 2, – 4) and C (– 1, 1, 2). Find the coordinates of the fourth vertex.
15. Let D(x, y, z) be the fourth vertex of the parallelogram ABCD.
In a parallelogram, the diagonal AC and BD bisects each other at point say O.
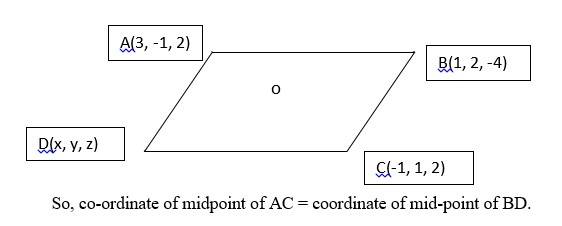
=>
=> (1, 0, 2) =
Equating the coordinates we get,
= 1
=>
=>
And
= 0
=>
And
= 2
=>
=>
=>
So, coordinates of fourth vertex is (1, –2, 8)
18. Find the coordinates of a point on y-axis which are at a distance of from the point P (3, –2, 5).
18. Let Q be the point on y-axis which are at a distance from point P. As Q is on y-axis it has the coordinates of form (0, y, 0).
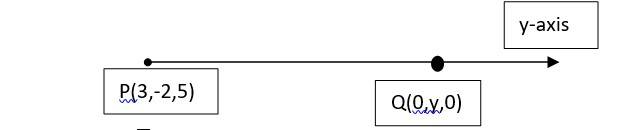
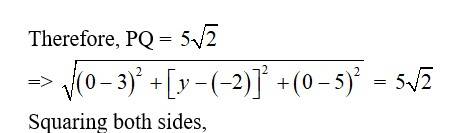
=>
=>
=>
=>
=>
So the coordinates Q are (0, 2, 0) and (0, –6, 0).
19. A point R with x-coordinate 4 lies on the line segment joining the points P(2, –3, 4) and Q (8, 0, 10). Find the coordinates of the point R.
[Hint Suppose R divides PQ in the ratio k : 1. The coordinates of the point R are given by
19. Given, x-coordinate of R = 4
Let R divides line segment joining points P(2, –3, 4) and Q(8, 0,10) internally in the ratio k : 1. Then coordinate of R is
=
Then,
= 4
=>
=>
=>
=>
=>
=>
Hence,
=
=
=
=
And,
z =
=
=
=
= 6
Therefore, coordinates of R is (4, –2, 6).
Class 11 Math Three Dimensional Geometry Exercise 11.1 NCERT Solution
1. A point is on the x-axis. What are its y-coordinate and z-coordinates?
1. When a point lies on x-axis, its y-coordinate and z-coordinate are zero.
Class 11 Math Ex 12.3 NCERT Solution
10. Find the coordinates of the point which divides the line segment joining the points (– 2, 3, 5) and (1, – 4, 6) in the ratio (i) 2 : 3 internally, (ii) 2 : 3 externally.
10. i. Let P(x, y, z) be the point which divides line segment joining (–2, 3, 5) and (1, –4, 6) internally in the ratio 2 : 3
Therefore,
x = = =
y = = =
z = = =
Thus, the required points are
ii. Let P(x, y, z) be the point which divides line segment joining (–2, 3, 5) and (1, –4, 6) externally in the ratio 2 : 3
Therefore,
x = = = –8
y = = = 17
z = = = 3
Thus, the required points are (–8, 17, 3).
11. Given that P (3, 2, – 4), Q (5, 4, – 6) and R (9, 8, –10) are collinear. Find the ratio in which Q divides PR.
11. Let point Q divides PR in the k : 1. Then co-ordinate of Q will be
=> (5, 4, –6) =
Equating the co-ordinates we get,
= 5
=>
=>
=>
=>
=>
=>
Putting in y-coordinate and z-coordinate
=
= (4 + 2) ÷
= 6 x
= 4
And
= (–5 – 4) ÷
= – 9 x
= – 6
Which is matching with the given co-ordinates of Q.
Hence, the ration in which Q divides PR is k : 1
= : 1
= 1 : 2
13. Using section formula, show that the points A (2, –3, 4), B (–1, 2, 1) and are collinear.
13. Let P divides AB in ratio k : 1. Then co-ordinates of point P are
=
Let us examine whether the value of k, the point P coincides with point C
Putting
=>
=>
Put in
=
=
=
And put in
=
=
= 2
Therefore, C is a point which divides AB internally in ratio 2 : 1 and is same as P. Hence A, B and C are collinear.
17. If the origin is the centroid of the triangle PQR with vertices P (2a, 2, 6), Q (– 4, 3b, –10) and R(8, 14, 2c), then find the values of a, b and c.
17. We know that, the centroid of a triangle with vertices (x1, y1, z1), (x2, y2, z2) and (x3, y3, z3) is
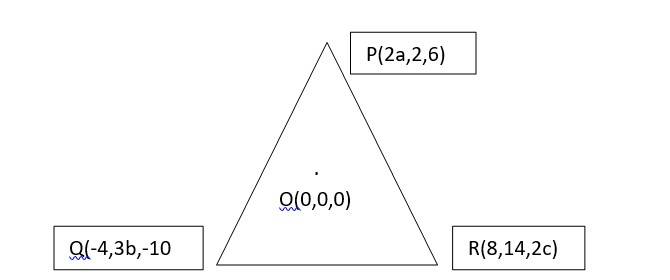
Equating the coordinates we get,
= 0
=>
=>
=>
=>
=>
And,
=>
=>
=>
=>
And,
=>
=>
=>
=>
=>
7. Verify the following:
(i) (0, 7, –10), (1, 6, – 6) and (4, 9, – 6) are the vertices of an isosceles triangle.
(ii) (0, 7, 10), (–1, 6, 6) and (– 4, 9, 6) are the vertices of a right angled triangle.
(iii) (–1, 2, 1), (1, –2, 5), (4, –7, 8) and (2, –3, 4) are the vertices of a parallelogram.
7. i. Let the points be P (0, 7, –10), Q (1, 6, –6) and R (4, 9, –6)
So,
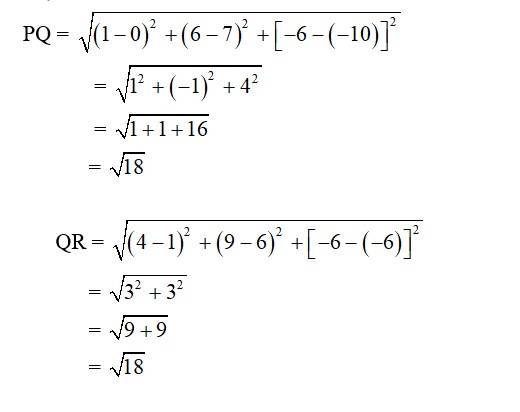




Class 11 Math Introduction to Three Dimensional Geometry Exercise 12.2 Solution
Three-dimensional geometry Exercise 11.1 focuses on more advanced topics, such as the distance between two points and finding collinear points, which help in determining the orientation of a line in three-dimensional space. Class 11 Math 3D Geometry Ex 11.2 consists of five questions, and solutions to all the questions are available. Students can check the solutions below.
Class 11 Math Three Dimensional Geometry Exercise 11.2 NCERT SolutionQ1. Find the distance between the following pairs of points:
|
| A.1. i. The distance between points (2, 3, 5) and (4, 3, 1) is |
| Q2. Show that the points (–2, 3, 5), (1, 2, 3) and (7, 0, –1) are collinear. |
| Q3. Verify the following: (i) (0, 7, –10), (1, 6, – 6) and (4, 9, – 6) are the vertices of an isosceles triangle. (ii) (0, 7, 10), (–1, 6, 6) and (– 4, 9, 6) are the vertices of a right angled triangle. (iii) (–1, 2, 1), (1, –2, 5), (4, –7, 8) and (2, –3, 4) are the vertices of a parallelogram. |
| A.3. i. Let the points be P(0, 7, –10), Q(1, 6, –6) and R(4, 9, –6) So, |
| Q4. Find the equation of the set of points which are equidistant from the points (1, 2, 3) and (3, 2, –1). |
| A.4. Let P(x, y, z) be the point equidistant from the given points (1, 2, 3) say A and (3, 2, –1) say B. So, PA = PB => = Squaring both sides, => = => => => => => => Therefore, the required equation of point is |
| Q5. Find the equation of the set of points P, the sum of whose distances from A (4, 0, 0) and B (– 4, 0, 0) is equal to 10. |
| A.5. Let P have the co-ordinates (x, y, z). Given that, PA + PB = 10 |
Class 11 Math Introduction to Three Dimensional Geometry Exercise 12.3 Solution
Class 11 Math Introduction to Three Dimensional Geometry Miscellaneous Exercise Solution
Explore exams which ask questions on Maths Ncert Solutions class 11th
Select your preferred stream
Maths Ncert Solutions class 11th Exam
Student Forum
Other Similar chapters for you
- Binomial Theorem
- Probability
- Statistics
- Mathematical Reasoning
- Limits and Derivatives
- Introduction to Three Dimensional Geometry
- Conic Sections
- Straight Lines
- Sequences and Series
- NCERT Maths 11th
- Permutations and Combinations
- Linear Inequalities
- Complex Numbers and Quadratic Equations
- Principle of Mathematical Induction
- Trigonometric Functions
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test