NCERT Chapter 14 Class 11 Maths – Probability Questions Solved

Q: 36. Fill in the blanks in following table: P(A) P(B) P(A ∩ B) P(A ∪ B) (i) 13 15 115 . . . (ii) 0.35 . . . 0.25 0.6 (iii) 0.5 0.35 . . . 0.7

36. (i) Given P (A) = 13 P (B) = 15 P (A∩B) = 115 So, P (A∪B) = P (A) + P (B) – P (A∩B) =13+15−115 =5+3−115 P (A∪B) = 715 (ii) Given P (A) = 0.35 P (B) =? P (A∩B) = 0.25 P (A∪B) = 0.6 So, P (A∪B) = P (A) + P (B) – P (A∩B) 0.6 = 0.35 + P (B) – 0.25 P (B) = 0.6 – 0.35 + 0.25 P (B) = 0.5 (iii) Given P (A) = 0.5 P (B) = 0.35 P (A∩B) =? P (A∪B) = 0.7 So, P (A∪B) = P (A) + P (B) – P (A∩B) 0.7 = 0.5 + 0.35 – P (A∩B) P (A∩B) = 0.5 + 0.35 – 0.7 P (A∩B) = 0.15

Updated on Sep 19, 2025 14:47 IST

By Pallavi Pathak, Assistant Manager Content

Class 11 Probability talks about the events, their occurrence, types, algebra, and complementary. The students will get to practice the exercises based on these and more topics. The step-by-step solutions will help students understand the right approach to solving questions based on probability.
Students can also download the Probability Class 11 PDF from this page and practice it offline. The Probability Class 11 NCERT Solutions are created by Shiksha's subject matter experts. Students can rely on these solutions for their exam preparation and get good marks in the Class 11 exam, CBSE and JEE Main exams.
To access the probability class 11 solutions and chapter-wise NCERT notes of Class 11 Maths with important topics and solved examples, read here.

Table of content

Key Highlights of Class 11 Maths Chapter 14 – Probability
Class 11 Math Probability: Key Topics, Weightage
Important Formulas of Probability Class 11
Class 11 Math Probability NCERT Solution PDF: Download Free PDF
Class 11 Math Probability NCERT Exercise 16.1 Solutions OLD NCERT*
Class 11 Maths Probability - FAQs

Key Highlights of Class 11 Maths Chapter 14 – Probability

See below the quick summary of Probability:

One of the key topics of the Class 11 Probability NCERT Solutions is the axiomatic approach of probability.
It covers events - a subset of the sample space, impossible event, sure event, and complementary event or 'not event'.
It includes event A or B, event A and B, event A and not B, mutually exclusive events, and exhaustive and mutually exclusive events.
In probability, the chapter covers equally likely outcomes and the probability of an event.

Are you looking for the quick revision notes for Physics, Chemistry, and Maths of Class 11? Do check here.

Class 11 Math Probability: Key Topics, Weightage

Class 11 probability covers events and probability. Understanding the key concepts of the NCERT Solutions Probability Class 11 is important for competitive exam preparation. See below the topics covered in the Probability Class 11:

Exercise	Topics Covered	Sub Topics Covered
14.1	Event	Occurrence of an event, Types of events, Algebra of events, Mutually exclusive events, Exhaustive events
14.2	Axiomatic Approach to Probability	Probability of an event, Probabilities of equally likely outcomes, Probability of the event ‘A or B’, Probability of event ‘not A’

Probability Class 11 Weightage for JEE Main

Exam	Number of Questions	Weightage
JEE Main	2-3 questions	6%

Important Formulas of Probability Class 11

Important Formulae for Probability

Probability of an Event:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}}$
Probability of Sure Event:
$P(S) = 1$
Probability of Impossible Event:
$P(\phi) = 0$
Complementary Events:
$P(E') = 1 - P(E)$
Addition Theorem for Two Events:
$P(A \cup B) = P(A) + P(B) - P(A \cap B)$
Mutually Exclusive Events (no common outcomes):
$P(A \cap B) = 0 \quad \text{thus} \quad P(A \cup B) = P(A) + P(B)$
General Probability Rules:
- For any event $A$ :
  $0 \leq P(A) \leq 1$
- Sum of probabilities of all elementary events of an experiment = 1.

Class 11 Math Probability NCERT Solution PDF: Download Free PDF

Students must download the Probability Class 11 PDF to get the well-structured solutions of the NCERT questions. It will help them score well in the Class 11 exam, CBSE Board and JEE Mains.

Chapter 5 Probability Class 11 NCERT Solutions: Download Free PDF

Class 11 Math Probability NCERT Exercise 16.1 Solutions OLD NCERT*

Class 11 NCERT Probability Exercise 16.1 deals with the fundamental concepts of probability. It covers several key topics, such as random experiments, sample spaces, events, and different types of events, including mutually exclusive, exhaustive, and complementary events. Students can find the solution to all 16 questions in the Probability exercise 16.1 below.

Class 11 Math Probability Ex 16.1 Solutions

Q1. A coin is tossed three times.

A.1. On tossing a coin the possible outcomes are that of a head or a tail. So, the angle space of tossing a coin three times is

S = {HHH, HHT, HTH, THH, TTH, THT, HTT, TTT}

Q2. A die is thrown two times.

A.2. When a dice is thrown, we have 36 the possible outcome.

Dice 2 Dice 1	1	2	3	4	5	6
1	(1, 1)	(1, 2)	(1, 3)	(1, 4)	(1, 5)	(1, 6)
2	(2, 1)	(2, 2)	(2, 3)	(2, 4)	(2, 5)	(2, 6)
3	(3, 1)	(3, 2)	(3, 3)	(3, 4)	(3, 5)	(3, 6)
4	(4, 1)	(4, 2)	(4, 3)	(4, 4)	(4, 5)	(4, 6)
5	(5, 1)	(5, 2)	(5, 3)	(5, 4)	(5, 5)	(5, 6)
6	(6, 1)	(6, 2)	(6, 3)	(6, 4)	(6, 5)	(6, 6)

Q3. A coin is tossed four times.

A.3. On tossing a coin the possible outcomes are Head and Tail. The sample space of tossing a coin four times is

S = {HHHH, THHH, HTHH, HHTH, HHHT, TTTT, HTTT, THTT, TTHT, TTTH, TTHH, HHTT, THTH, HTHT, THHT, HTTH}

Q4. A coin is tossed and a die is thrown.

A.4. The possible outcomes of throwing a coin and rolling a dice are Head and tail and 1, 2, 3, 4, 5 and 6 respective. So, the desired sample space is

S = {(H, 1), (H, 2), (H, 3), (H, 4), (H, 5), (H, 6), (T, 1), (T, 2), (T, 3), (T, 4), (T, 5), (T, 6)}

Commonly asked questions

36. Fill in the blanks in following table:

P(A) P(B) P(A ∩ B) P(A ∪ B)

(i) $\frac{1}{3}$ $\frac{1}{5}$ $\frac{1}{15}$ . . .

(ii) 0.35 . . . 0.25 0.6

(iii) 0.5 0.35 . . . 0.7

36. (i) Given P (A) = $\frac{1}{3}$

P (B) = $\frac{1}{5}$

P (A∩B) = $\frac{1}{15}$

So, P (A∪B) = P (A) + P (B) – P (A∩B)

$= \frac{1}{3} + \frac{1}{5} - \frac{1}{15}$

$= \frac{5 + 3 - 1}{15}$

P (A∪B) = $\frac{7}{15}$

(ii) Given P (A) = 0.35

P (B) =?

P (A∩B) = 0.25

P (A∪B) = 0.6

So, P (A∪B) = P (A) + P (B) – P (A∩B)

0.6 = 0.35 + P (B) – 0.25

P (B) = 0.6 – 0.35 + 0.25

P (B) = 0.5

(iii) Given P (A) = 0.5

P (B) = 0.35

P (A∩B) =?

P (A∪B) = 0.7

So, P (A∪B) = P (A) + P (B) – P (A∩B)

0.7 = 0.5 + 0.35 – P (A∩B)

P (A∩B) = 0.5 + 0.35 – 0.7

P (A∩B) = 0.15

6. 2 boys and 2 girls are in Room X, and 1 boy and 3 girls in Room Y. Specify the sample space for the experiment in which a room is selected and then a person.

6. Let us denote B1, B2 to be the boys and G1, G2 to be the girls in Room X and B3 to be the boy and G3, G4, G5 to the girls in Room Y. Hence the desired sample space is

S = { (X, B1), (X, B2), (X, G1), (X, G2), (Y, B3), (Y, G3), (Y, G4), (Y, G5)}

23. Refer to question 6 above, state true or false: (give reason for your answer)

(i) A and B are mutually exclusive

(ii) A and B are mutually exclusive and exhaustive

(iii) A = B′

(iv) A and C are mutually exclusive

(v) A and B′ are mutually exclusive.

(vi) A′, B′, C are mutually exclusive and exhaustive.

23. (i) A ∩B = { (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),

(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),

(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}∩ { (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),

(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),

(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)}

A ∩B =∅

Hence, A and B are mutually exclusive.

The given statement is true.

(ii) A ∪B = { (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),

(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),

(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}∩ { (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),

(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),

(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)}

= { (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),

(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),

(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),

(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),

(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6),

(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}

= S

Hence, A B = S and A∩ B =∅

A and B are mutually exclusive and mutually exhaustive.

So, the give statement is true.

(iii) A = { (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),

(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),

(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}

B = S – B = { (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),

(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),

(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),

(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),

(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6),

(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)} – { (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (3, 1), (3, 2), (3, 3), (3, (4), (3, 5), (3, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)}

= { (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),

(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),

(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}

B' = A

Hence, the given relation is true.

(iv) A ∩C = { (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),

(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),

(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}∩ { (1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (4, (1)}

= { (2, 1), (2, 2), (2, 3), (4, 1)}≠∅

So, A∩ C≠∅

i.e., A and C are not mutually exclusive.

Hence, the given statement is false.

(v) A∩ B' = A∩ A = A≠∅ { B' = A}

Hence A∩B'≠∅ i.e., A and B are not mutually exclusive.

So, the given statement is false.

(vi) As A' = B

B = A

So, A'∩B = B∩A =∅

A'∩ C = B∩C = { (1, 1), (1, 2), (1, 3), (1, 4), (3, 1), (3, 2)}=∅

B'∩C = A∩C = { (2, 1), (2, 2), (2, 3), (4, 1)}=∅

Hence, A', B' and C are not mutually exclusive.

The given statement is false.

3. A coin is tossed four times.

3. On tossing a coin the possible outcomes are Head and Tail. The sample space of tossing a coin four times is

S = {HHHH, THHH, HTHH, HHTH, HHHT, TTTT, HTTT, THTT, TTHT, TTTH, TTHH, HHTT, THTH, HTHT, THHT, HTTH}

22. Two dice are thrown. The events A, B and C are as follows:

A: getting an even number on the first die.

B: getting an odd number on the first die.

C: getting the sum of the numbers on the dice ≤ 5.

Describe the events

(i) A′ (ii) Not B (iii) A or B

(iv) A and B (v) A but not C

(vi) B or C (vii) B and C (viii) A ∩ B′ ∩ C′

22. The sample space of the experiment is

S = { (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),

(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),

(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),

(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),

(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6),

(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}

Now, A = { (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),

(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),

(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}

B = { (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),

(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),

(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)}

C = { (1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (4, 1)}

(i) A? = S – A = Sample space – getting even number on 1st dice = getting odd number on 1st dice = B

(ii) B' = S – B = Sample space – getting odd number on 1st dice = getting even number on 1st dice = A

(iii) A or B = A∪B = (getting even on 1st die)∪ (getting odd o 1st dice) = Sample space = S

(iv) A and B = A∩ B = (getting even on 1st dice)∩ (getting odd on 1st dice) =∅

(v) A but not C = { (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)} – { (1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (4, 1)}

A – C = { (2, 4), (2, 5), (2, 6), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}

(vi) B or C = B∪C = { (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (3, 1), (3, 1), (3, 3), (3, 4), (3, 5), (3, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)}∪ { (1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (4, 1)}

= { (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)}

(vii) B and C = B∩ C = { (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)}∩ { (1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (4, 1)} = { (1, 1), (1, 2), (1, 3), (1, 4), (3, 1), (3, 2), (4, 1)}

(viii) A∩B ∩C = A ∩A ∩C (as B' = A)

= A ∩C' (A ∩A = A)

So, C' = S – C = { (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),

(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),

(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),

(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),

(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6),

(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)} – { (1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (4, 1)}

C' = { (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 3), (3, 4), (3, 5), (3, 6), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}

So, A ∩B ∩ C' = (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),

(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),

(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}

{ (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 3), (3, 4), (3, 5), (3, 6), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, (3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}

= { (2, 4), (2, 5), (2, 6), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}

18. A die is thrown. Describe the following events:

(i) A: a number less than 7

(ii) B: a number greater than 7

(iii) C: a multiple of 3 (iv) D: a number less than 4

(v) E: an even number greater than 4 (vi) F: a number not less than 3

Also find A ∪ B, A ∩ B, B ∪ C, E ∩ F, D ∩ E, A – C, D – E, E ∩ F′, F′

18. The sample space of the experiment is

S = {1, 2, 3, 4, 5, 6}

(i) A = {1, 2, 3, 4, 5, 6}

(ii) B =∅

(iii) C = {3, 6}

(iv) D = {1, 2, 3}

(v) E = {6}

(vi) F = {3, 4, 5, 6}

A ∪ B = {1, 2, 3, 4, 5, 6}∩ {∅}= ∅h

= {1, 2, 3, 4, 5, 6}

A ∩B = {1, 2, 3, 4, 5, 6}∩ {∅}

B ∪C = ∅∪ {3, 6) = {3, 6}

E∩ F = {6}∩ {3, 4, 5, 6} = {6}

D∩ E = {1, 2, 3}∩ {6} =∅

A – C = {1, 2, 3, 4, 5, 6} – {3, 6} = {1, 2, 4, 5}

D – E = {1, 2, 3} – {6} = {1, 2, 3}

E ∩F' = E∩ (S – F) = {6}∩ [ {1, 2, 3, 4, 5, 6} – {3, 4, 5, 6}]

= {6} ∩ {1, 2}

=∅

F' = S – F = {1, 2, 3, 4, 5, 6} – {3, 4, 5, 6} = {1, 2}

31. Three coins are tossed once. Find the probability of getting

(i) 3 heads

(ii) 2 heads

(iii) Atleast 2 heads

(iv) Atmost 2 heads

(v) No head

(vi) 3 tails

(vii) Exactly two tails

(viii) No tail

(ix) Atmost two tails

31. When three coins are tosses we have the sample space,

S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}

So, n (S) = 8

(i) Let A: 3 heads occurs.

A = {HHH}

So, n (A) = 1

? P (A) = $\frac{1}{8}$

(ii) Let B: 2 heads occurs

B = {HHT, HTH, THH}

So, n (B) = 3

? P (B) = $\frac{3}{8}$

(iii) Let C: at least 2 heads occurs i.e. 2 heads or more

C = {HHT, HTH, THH, HHH}

So, n (C) = 4

? P (C) = $\frac{4}{8} = \frac{1}{2}$

(iv) Let D: at most 2 heads occurs i.e. 2 heads or less

D = {TTT, HTT, THT, TTH, HHT, HTH, THH}

So, n (D) = 7

? P (D) = $\frac{7}{8}$

(v) Let E: no head occurs

E = {TTT}

So, n (E) = 1

? P (E) = $\frac{1}{8}$

(vi) Let F: 3 tails occurs

F = {TTT}

So, n (F) = 1

? P (F) = $\frac{1}{8}$

(vii) Let G: exactly two tails occurs

G = {TTH, THT, HTT}

So, n (G) = 3

? P (G) = $\frac{3}{8}$ .

(viii) Let H: no tail occurs

H = {HHH}

So, n (H) = 1

? P (H) = $\frac{1}{8}$ .

(ix) Let I: atmost two tails i.e. two tails or less

I = {HHH, THH, HTH, HHT, HTT, THT, TTH}

So, n (I) = 7

? P (I) = $\frac{7}{8}$

51. A and B are two events such that P(A) = 0.54, P(B) = 0.69 and P(A ∩ B) = 0.35.

Find (i) P(A ∪ B) (ii) P(A´ ∩ B´) (iii) P(A ∩ B´) (iv) P(B ∩ A´)

51. Given, P (A) = 0.54

P (B) = 0.69.

P (A ∩ B) = 0.35.

(i) P (A ∪ B) = P (A) + P (B) - P (A ∩ B)

= 0.54 + 0.69 - 0.35

= 0. 88

(ii) P (A? ∩ B? ) = P (A ∩ B)? = 1 - P (A ∪ B) = 1 - 0.88 = 0.12

(iii) P (A ∩ B? ) = P (A) - P (A ∩ B)

= 0.54 - 0. 35 = 0.19

(iv) P (B ∩ A? ) = P (B) - P (A ∩ B) = 0.69 - 0.35 = 0.34

2. A die is thrown two times.

2. When a dice is thrown, we have 36 the possible outcome.

Dice 2 Dice 1	1	2	3	4	5	6
1	(1, 1)	(1, 2)	(1, 3)	(1, 4)	(1, 5)	(1, 6)
2	(2, 1)	(2, 2)	(2, 3)	(2, 4)	(2, 5)	(2, 6)
3	(3, 1)	(3, 2)	(3, 3)	(3, 4)	(3, 5)	(3, 6)
4	(4, 1)	(4, 2)	(4, 3)	(4, 4)	(4, 5)	(4, 6)
5	(5, 1)	(5, 2)	(5, 3)	(5, 4)	(5, 5)	(5, 6)
6	(6, 1)	(6, 2)	(6, 3)	(6, 4)	(6, 5)	(6, 6)

46. 4 cards are drawn from a well – shuffled deck of 52 cards. What is the probability of obtaining 3 diamonds and one spade?

46. Total number of ways of drawing 4 cards from a duck of 52 cards, n (s) = ⁵²C₄

Total no. of diamond cards = 13

Similarly, total. no. of spades cards = 13

33. A letter is chosen at random from the word ‘ASSASSINATION’. Find the probability that letter is (i) A vowel (ii) A consonan

33. The sample space of word is

S = {A, S, A, S, I, N, A, T, I, O, N}

So, n (S) = 13.

(i) Let A: word is a vowel

A = {A, I, A, I, O}

So, n (A) = 6

? P (A) = $\frac{6}{13}$

(ii) Let B: Word is a consonant

B = {S, N, T, N}

So, n (B) = 7

? P (B) = $\frac{7}{13}$ .

42. In an entrance test that is graded on the basis of two examinations, the probability of a randomly chosen student passing the first examination is 0.8 and the probability of passing the second examination is 0.7. The probability of passing atleast one of them is 0.95. What is the probability of passing both?

42. Let A: Student passes 1st examination

So, P (A) = 0.8

And B: Student passes 2nd examination

So, P (B) = 0.7

Also probability of passing at least one examination is P (A∪B) = 0.95

Therefore, P (A∪B) = P (A) + P (B) – P (A∩B)

0.95 = 0.8 + 0.7 – P (A∩B)

P (A∩B) = 0.8 + 0.7 – 0.95

P (A∩B) = 0.55

Hence, probability of passing both examination is 0.55.

7. One die of red colour, one of white colour and one of blue colour are placed in a bag. One die is selected at random and rolled, its colour and the number on its uppermost face is noted. Describe the sample space.

7. One rolling a dice we have the possible outcome 1, 2, 3, 4, 5 and 6. Let us denote R, W and B as red, white and blue respectively. So, the desired sample space is

S = { (R, 1), (R, 2), (R, 3), (R, 4), (R, 5), (R, 6), (W, 1), (W, 2), (W, 3), (W, 4), (W, 5), (W, 6), (B, 1), (B, 2), (B, 3), (B, 4), (B, 5), (B, 6)}

5. A coin is tossed and then a die is rolled only in case a head is shown on the coin.

5. When a coin is tossed we have the outcomes of a head or a tail and when a dieice is rolled we have the outcome 1, 2, 3, 4, 5 or 6. So, the desired sample space is

S = {T, (H, 1), (H, 2), (H, 3), (H, 4), (H, 5), (H, 6)}

19. An experiment involves rolling a pair of dice and recording the numbers that come up. Describe the following events:

A: the sum is greater than 8, B: 2 occurs on either die

C: the sum is at least 7 and a multiple of 3.

Which pairs of these events are mutually exclusive?

19. The sample space of the experiment is

S = { (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),

(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),

(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),

(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),

(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6),

(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}

And A = { (3, 6), (4, 5), (4, 6), (5, 4), (5, 5), (5, 6), (6, 3), (6, 4), (6, 5), (6, 6)}

B = { (1, 2), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 2), (4, 2), (5, 2), (6, 2)}

C = { (3, 6), (4, 5), (5, 4), (6, 3), (6, 6)}

Now, A∩ B = { (3, 6), (4, 5), (4, 6), (5, 4), (5, 5), (5, 6), (6, 3), (6, 4), (6, 5), (6, 6)}∩ { (1, 2), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 2), (4, 2), (5, 2), (6, 2)}

A ∩B =∅

B∩ C = { (1, 2), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 2), (4, 2), (5, 2), (6, 2)}∩ { (3, 6), (4, 5), (5, 4), (6, 3), (6, 6)}

A∩C = { (3, 6), (4, 5), (4, 6), (5, 4), (5, 5), (5, 6), (6, 3), (6, 4), (6, 5), (6, 6)}∩ { (3, 6), (4, 5), (5, 4), (6, 3), (6, 6)}

= { (3, 6), (4, 5), (5, 4), (6, 3), (6, 6)}

So, (A and B) and (B and C) are mutually exclusive.

1. A coin is tossed three times.

1. On tossing a coin the possible outcomes are that of a head or a tail. So, the angle space of tossing a coin three times is

S = {HHH, HHT, HTH, THH, TTH, THT, HTT, TTT}

43. The probability that a student will pass the final examination in both English and Hindi is 0.5 and the probability of passing neither is 0.1. If the probability of passing the English examination is 0.75, what is the probability of passing the Hindi examination?

43. Let A: student passing in Hindi

B: student passing in English

Given, P (B) = 0.75

P (A∩B) = 0.5, passing both subject

And P (A'∩B') = 0.1, i.e., passing neither subject

P (A∪B)' = 0.1

1 – P (A∪B) = 0.1

P (A∪B) = 1 – 0.1

P (A∪B) = 0.9

Hence, P (A∪B) = P (A) + P (B) – P (A∩B)

P (A) = P (A∪B) + P (A∩B) – P (B)

P (A) = 0.9 + 0.5 – 0.75 = 0.65

? The probability of passing Hindi examination is 0.65.

28. A fair coin with 1 marked on one face and 6 on the other and a fair die are bothtossed. find the probability that the sum of numbers that turn up is (i) 3 (ii) 12

28. The sample space of the experiment is

S = { (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5) (6, 6)}

So, n (S) = 12.

(i) Let E be event such that sum of numbers that turn up is 3. Then,

E = { (1, 2)}

So, n (E) = 1

P (E) = $\frac{n (E)}{n (S)} = \frac{1}{12}$ .

(ii) Let F be event such that sum of number than turn up is 12. Then,

F = { (6, 6)}

So, n (F) = 1

P (F) = $\frac{n (F)}{n (S)} = \frac{1}{12}$ .

38. If E and F are events such that P(E) = $\frac{1}{4}$ , P(F) = $\frac{1}{2}$ and P(E and F) = $\frac{1}{8}$ , find

(i) P(E or F), (ii) P(not E and not F).

38. Given, P (E) = $\frac{1}{4}$

P (F) = $\frac{1}{2}$

P (E and F) = P (E∩F) = $\frac{1}{8}$

(i) P (E or F) = P (E∪F) = P (E) + P (F) – P (E∩F)

$= \frac{1}{4} + \frac{1}{2} - \frac{1}{8}$

$= \frac{2 + 4 - 1}{8}$

$= \frac{5}{8}$

(ii) P (not E and not F) = P (E'∩F') = P (E∪F)' = 1 – P (E∪F)

$= 1 - \frac{5}{8} = \frac{8 - 5}{8}$

$= \frac{3}{8}$

39. Events E and F are such that P(not E or not F) = 0.25, State whether E and F aremutually exclusive.

39. Given, P (not E or not F) = 0.25

P (E'∪F') = 0.25

P (E∩F)' = 0.25

1 – P (E∩F) = 0.25

P (E∩F) = 1 – 0.25

P (E∩F) = 0.75≠ 0

Hence, E and F are not mutually exclusive events.

52. From the employees of a company, 5 persons are selected to represent them inthe managing committee of the company. Particulars of five persons are as follows:

1. No. Name Sex Age in years

2. Harish M 30

3. Rohan M 33

4. Sheetal F 46

5. Alis F 28

6. Salim M 41

A person is selected at random from this group to act as a spokesperson. What is the probability that the spokesperson will be either male or over 35 years?

52. Total no. of person selected to represent the company n (s) = 5.

Let A: person is male.

A = {Harish, Rohan, Salim}

n (A) = 3

And B: person has one 35 yes of age.

B = {Sheetal, Salim}

n (B) = 2

And A ∩ B = {Salim}

n (A ∩ B) = 1

Probability that person is either male or over 35 years.

= P (A ∪ B) = P (A) + P (B) P (A ∩ B)

$= \frac{n (A)}{n (S)} + \frac{n (B)}{n (S)} - \frac{n (A \cap B)}{n (S)}$

= $= \frac{3}{5} + \frac{2}{5} - \frac{1}{5}$

$= \frac{3 + 2 - 1}{5} = \frac{4}{5}$

20. Three coins are tossed once. Let A denote the event ‘three heads show”, B denote the event “two heads and one tail show”, C denote the event” three tails

show and D denote the event ‘a head shows on the first coin”. Which events are

(i) Mutually exclusive ? (ii) Simple? (iii) Compound?

20. The sample space of the experiment is

S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}

Now, A = {HHH}

B = {HHT, HTH, THH}

C = {TTT}

D = {HHH, HHT, HTH, HTT}

(i) A∩ B = {HHH}∩ {HHT, HTH, THH} =∅

A ∩ C = {HHH}∩ {TTT} =∅

A∩ D = {HHH}∩ {HHH, HTH, HTT} = {HHH}

B ∩ C = {HHT, HTH, THH}∩ {TTT} =∅

B∩ D = {HHT, HTH, THH}∩ {HHH, HHT, HTH, HTT} = {HHT, HTH}

C∩ D = {TTT}∩ {HHH, HHT, HTH, HTT} =∅

Hence, (A, B), (A, C), (B, C) and (C, D) are pairs of mutually exclusive events.

(ii) Simple event are those which has only one sample point. So, the simple event are A and C.

(iii) Event having more than one sample point are called compound event. So, B and D are compound event.

4. A coin is tossed and a die is thrown.

4. The possible outcomes of throwing a coin and rolling a dice are Head and tail and 1, 2, 3, 4, 5 and 6 respective. So, the desired sample space is

S = { (H, 1), (H, 2), (H, 3), (H, 4), (H, 5), (H, 6), (T, 1), (T, 2), (T, 3), (T, 4), (T, 5), (T, 6)}

15. A coin is tossed. If it shows a tail, we draw a ball from a box which contains 2 red and 3 black balls. If it shows head, we throw a die. Find the sample space for this experiment.

15. The possible outcome when a coin is tossed is a head or a tail. When a dice is thrown we can have the possible outcomes 1, 2, 3, 4, 5 and 6. Let R1, R2 be the two red balls and B1, B2, B3 be the two black balls. So, the desired sample space is

S = { (T, R1), (T, R2), (T, B1), (T, B2), (T, B3), (H, 1), (H, 2), (H, 3), (H, 4), (H, 5), (H, 6)}

16. A die is thrown repeatedly until a six comes up. What is the sample space for this experiment?

16. When a die is drawn we can have 1, 2, 3, 4, 5 and 6. So, sample space of throwing dice until a six comes up is

S = { (6, (1, 6), (2, 6), (3, 6), (4, 6), (5, 6), (1, 6), (1, 2, 6), (1, 3, 6), (1, 4, 6), (1, 5, 6), (1, 6)……., (1, 5, 6), (1, 6)……… (1, 5, 6)………}

Hence, the sample space is indefinite.

14. An experiment consists of rolling a die and then tossing a coin once if the number on the die is even. If the number on the die is odd, the coin is tossed twice. Write the sample space for this experiment.

14. The possible outcome when a coin is tossed is a head or a tail. When a die is thrown we can have the possible outcome 1, 2, 3, 4, 5 and 6. So, the desired sample space is

S = { (2, H), (2, T), (4, H), (4, T), (6, H), (6, T), (1, H, H), (1, H, T), (1, T, H), (1, T, T), (3, H, H), (3, H, T), (3, T, H), (3, T, T), (5, H, H), (5, H, T), (5, T, H), (5, T, T)}

26. A die is thrown, find the probability of following events:

(i) A prime number will appear,

(ii) A number greater than or equal to 3 will appear,

(iii) A number less than or equal to one will appear,

(iv) A number more than 6 will appear,

(v) A number less than 6 will appear.

26. The sample space of throwing s dice is

S = {1, 2, 3, 4, 5, 6}, n (S) = 6.

(i) Let A be event such that a prime number will appear. Then,

A = {2, 3, 5}

? n (A) = 3

Here; P (A) = $\frac{n (A)}{n (S)} = \frac{3}{6} = \frac{1}{2}$

(ii) Let B be event such that a number greater than or equal to 3 will appear. Then

B = {3, 4, 5, 6}

So, n (B) = 4

Therefore P (B) = $\frac{n (B)}{n (S)} = \frac{4}{6} = \frac{2}{3}$

(iii) Let C be event such that a number less than or equal to one will appear. Then,

C = {1}

So, n (C) = 1

? P (C) = $\frac{n (C)}{n (S)} = \frac{1}{6}$

(iv) Let D be event such that a number more than 6 appears. Then,

D =∅

So, n (D) = 0

? P (D) = $\frac{n (D)}{n (S)} = \frac{0}{6} = 0$

(v) Let E be event such that a number less than 6 appears. Then

E = {1, 2, 3, 4, 5}

So, n (E) = 5

? P (E) = $\frac{n (E)}{n (S} = \frac{5}{6}$

27. A card is selected from a pack of 52 cards.

(a) How many points are there in the sample space?

(b) Calculate the probability that the card is an ace of spades.

(c) Calculate the probability that the card is (i) an ace (ii) black card.

27. (a) Since there are 52 cards in the sample space,

n (S) = 52.

So, there are 52 sample points.

(b) In a deck of 52 cards there are 4 ace cards of which only one is of spades.

Hence, if A be an event of getting an ace of spades.

n (A) = 1

So, P (A) = $\frac{n (A)}{n (S)} = \frac{1}{52}$ .

(c) (i) Let B be an event of drawing an ace. As there are 4 ace cards we have,

n (B) = 4

So, P (B) = $\frac{n (B)}{n (S)} = \frac{4}{52} = \frac{1}{13}$ .

(ii) Let D be an event of drawing black cards. Since there are 26 black cards we have,

n (D) = 26.

So, P (D) = $\frac{n (D)}{n (S)} = \frac{26}{52} = \frac{1}{2}$

29. There are four men and six women on the city council. If one council member is selected for a committee at random, how likely is it that it is a woman?

29. Number of women in the city council n (A) = 6

As there are four men and six women the total number of person in the sample space is 4 + 6 = 10.

So, n (S) = 10

P (A) = $\frac{n (A)}{n (S)} = \frac{6}{10} = \frac{3}{5}$

30. A fair coin is tossed four times, and a person win Re 1 for each head and lose Rs 1.50 for each tail that turns up.

From the sample space calculate how many different amounts of money you can have after four tosses and the probability of having each of these amounts.

30. When a coin is tossed four times we have the sample space,

S = {HHHH, HHHT, HHTH, HTHH, THHH, HHTT, THHT, TTHH, THTH, HTHT, HTTH, TTTH, TTHT, THTT, HTTT, TTTT}

So, n (S) = 16.

Case I: When the outcome is all head, the amount is 1 + 1 + 1 + 1 =? 4 gain

Case II: When the outcome is 3 head and one tail, the amount is

1 + 1 + 1 – 1.50 = 3 – 1.50 =? 1.50 gain

Case III: When the outcome is 2 head and 2 tail, the amount is

1 + 1 – 1.50 – 1.50 = 2 – 3 =? 1 lose.

Case IV: When the outcome is 1 head and 3 tail, the amount is

1 – 1.50 – 1.50 – 1.50 = 1 – 4.50 =? 3.50 lose.

Case V: When the outcome is all tail, the amount is

–1.50 – 1.50 – 1.50 – 1.50 = –6 =? 6 lose.

Let A be event such that person wins ?4. Then,

A = {HHHH}

So, n (A) = 1

? P (A) = $\frac{1}{16}$

Let B: person wins ?1.5. Then,

B = {HHHT, HHTH, HTHH, THHH}

So, n (B) = 4

? P (B) = $\frac{4}{16} = \frac{1}{4}$

Let C: person loses ?1. Then,

C = {HHTT, THHT, TTHH, THTH, HTHT, HTTH}

So, n (C) = 6

? P (C) = $\frac{6}{16} = \frac{3}{8}$

Let D: person loses ?3.50. Then,

D = {HTTT, THTT, TTHT, TTTH}

So, n (D) = 4

? P (D) = $\frac{4}{16} = \frac{1}{4}$

Let E: person loses ?6. Then,

E = {TTTT}

So, n (E) = 1

? P (E) = $\frac{1}{16}$ .

32. If $\frac{2}{11}$ is the probability of an event, what is the probability of the event ‘not A’.

32. Let A be the event

Given that, P (A) = $\frac{2}{11}$

So, P (not A) = P (S) – P (A) = $1 - \frac{2}{11} = \frac{11 - 2}{11} = \frac{9}{11}$

35. Check whether the following probabilities P(A) and P(B) are consistently defined

(i) P(A) = 0.5, P(B) = 0.7, P(A ∩ B) = 0.6

(ii) P(A) = 0.5, P(B) = 0.4, P(A ∪ B) = 0.8

35. Given P (A) = 0.5

P (B) = 0.7

And P (A∩B) = 0.6

As P (A∩B) > P (A) which is not possible.

The given probabilities are not consistently defined.

(ii) Given, P (A) = 0.5

P (B) = 0.4

And P (A∪B) = 0.8

So, P (A∪B) = P (A) + P (B) – P (A∩B)

0.8 = 0.5 + 0.4 – P (A∩B)

P (A∩B) = 0.5 + 0.4 – 0.8

P (A∩B) = 0.1

Hence, P (A∩B) < P (A) and P (A∩B) < P (B)

The given probabilities are consistently defined.

37. Given P(A) = $\frac{3}{5}$ and P(B) = $\frac{1}{5}$ . Find P(A or B), if A and B are mutually exclusive events.

37.

Given P (A) = $\frac{3}{5}$

P (B) = $\frac{1}{5}$

As A and B are mutually exclusive events,

P (A∩B) = 0

Hence, P (A∪B) = P (A) + P (B) – P (A∩B)

$= \frac{3}{5} + \frac{1}{5} - 0$

$= \frac{4}{5}$

8. An experiment consists of recording boy–girl composition of families with 2 children.

What is the sample space if we are interested in knowing whether it is a boy or girl in the order of their births?

What is the sample space if we are interested in the number of girls in the family?

8. Let us denote boys and girls by B and G.

(i) The desired sample space whether a boy or girl are the children according to their birth.

S = {BB, BG, GB, GG}

(ii) A family of two children can be two girls, one girl or no girl. So, the desired sample space is S = {0, 1, 2}

9. A box contains 1 red and 3 identical white balls. Two balls are drawn at random in succession without replacement. Write the sample space for this experiment.

9. Let us denote the red and white balls by R and W. We are to draw one ball and then another ball without replacement. So, the desired sample space is

S = {RW, WR, WW}

11. An experiment consists of tossing a coin and then throwing it second time if a head occurs. If a tail occurs on the first toss, then a die is rolled once. Find the sample space.

11. The possible outcomes when a coin is tossed is a Head or a Tail. And the possible outcomes when a die is rolled is 1, 2, 3, 4, 5 or 6.

By condition, when a head occurs or first toss the coin is tossed again and if a tail occurs on first toss a die is rolled. So, the required sample space is

S = { (H, H), (H, T), (T, 1), (T, 2), (T, 3), (T, 4), (T, 5) and (T, 6)}

11. Suppose 3 bulbs are selected at random from a lot. Each bulb is tested and classified as defective (D) or non – defective(N). Write the sample space of this experiment.

11. Let us denote the non-defective and defective bulbs by 'N' and 'D'. So, that the sample space of selecting 3 bulbs from a lot is.

S = {NNN, NND, NDN, DNN, DDN, NDD, DND, DDD}

17. A die is rolled. Let E be the event “die shows 4” and F be the event “die shows even number”. Are E and F mutually exclusive?

17. The sample space of the experiment is

S = {1, 2, 3, 4, 5, 6} and E = {4}

F = {2, 4, 6}

So, E∩ F = {4} ∩ {2, 4, 6} = {4} ≠

Therefore E and F are not mutually exclusive.

21. Three coins are tossed. Describe

(i) Two events which are mutually exclusive.

(ii) Three events which are mutually exclusive and exhaustive.

(iii) Two events, which are not mutually exclusive.

(iv) Two events which are mutually exclusive but not exhaustive.

(v) Three events which are mutually exclusive but not exhaustive.

21. The sample space of the experiment is

S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}

(i) Let A and B be two events such that

A: only head occurs

A = {HHH}

B: only tail occurs

B = {TTT}

And A ∩B = {HHH}∩ {TTT} =∅

(ii) Let A, B and C be two events such that

A: at most one head (i.e., the event in which we get maximum one head; one head or no head at all) occurs

So, A = {HTT, THT, TTH, TTT}

B: exactly two head occurs

So, B = {HHT, HTH, THH}

C: all are heads

So, C = {HHH}

Hence, A ∩ B = {HTT, THT, TTH, TTT} ∩ {HHT, HTH, THH} =∅

A ∩C = {HTT, THT, TTH, TTT} ∩ {HHH} =∅

B∩ C = {HHT, HTH, THH}∩ {HHH} =∅

And A∪ B ∪C = {HTT, THT, TTH, TTT}∪ {HHT, HTH, THH}∪ {HHH} = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}

= S

Therefore, A, B and C are three events which are mutually exclusive and exhaustive.

(iii) Let A and B be two such that

A: head occurs

So, A = {HHH, HHT, HTH, HTT, THH, THT, TTH}

B: tail occurs

So, B = {HHT, HTH, HTT, THH, THT, TTH, TTT}

Now, A ∩B = {HHH, HHT, HTH, HTT, THH, THT, TTH}∩ {HHT, HTH, HTT, THH, THT, TTH, TTT}

= {HHT, HTH, HTT, THH, THT, TTH} =∅

Hence A and B are not mutually exclusive.

(iv) Let A and B be two events such that

A: only head occurs

So, A = {HHH}

B = only tail occurs

So, B = {TTT}

Hence, A∩ B = {HHH}∩ {TTT} =∅

So, A ∩B =∅

But A∪ B = {HHH}∪ {TTT} = {HHH, TTT}≠ S

Therefore A and B are two events which are mutually exclusive but not exhaustive.

(v) Let A, B and C be three events such that

A: only head occurs

So, A = {HHH}

B: only tail occurs

So, B = {TTT}

C: getting one tail

So, C = {THH, HTH, HHT}

Hence, A∩ B = {HHH} ∩ {TTT} =∅

A∩ C = {HHH} ∩ {THH, HTH, HHT} =∅

B∩C = {TTT}∩ {THH, HTH, HHT} =∅

And A ∪B∪C = {HHH} ∪ {TTT}∪ {THH, HTH, HHT} = {HHH, TTT, THH, HTH, HHT} ≠ S

Therefore A, B and C are three mutually exclusive but not exhaustive.

12. A coin is tossed. If the out come is a head, a die is thrown. If the die shows up an even number, the die is thrown again. What is the sample space for the experiment?

12. When a coin is thrown we have the possible outcome of a head or a tail. And when a dice is thrown we have the possible outcomes 1, 2, 3, 4, 5 and 6. So, the desired sample space is

S = {T, (H, 1), (H, 2, 1), (H, 2, 2), (H, 2, 3), (H, 2, 4), (H, 2, 5), (H, 2, 6), (H, 3), (H, 4, 1), (H, 4, 2), (H, 4, 3), (H, 4, 4), (H, 4, 5), (H, 4, 6), (H, 5), (H, 6, 1), (H, 6, 2), (H, 6, 3), (H, 6, 4), (H, 6, 5), (H, 6, 6)}

13. The numbers 1, 2, 3 and 4 are written separately on four slips of paper. The slips are put in a box and mixed thoroughly. A person draws two slips from the box, one after the other, without replacement. Describe the sample space for the experiment.

13. The possible numbers to be chosen are 1, 2, 3 and 4. The sample space of drawing two slips one after another without replacement is

S = { (1, 2), (1, 3), (1, 4), (2, 1), (2, 3), (2, 4), (3, 1), (3, 2), (3, 4), (4, 1), (4, 2), (4, 3)}

24. Which of the following can not be valid assignment of probabilities for outcomes

of sample Space S = {ω₁, ω₂, ω₃, ω₄, ω₅, ω₆, ω₇,}

Assignment ω ₁ ω ₂ ω ₃ ω ₄ ω ₅ ω ₆ ω ₇

(a) 0.1 0.01 0.05 0.03 0.01 0.2 0.6

(b)

(c) 0.1 0.2 0.3 0.4 0.5 0.6 0.7

(d) – 0.1 0.2 0.3 0.4 – 0.2 0.1 0.3

(e) $\frac{\bar{1}}{\bar{14}}$ $\frac{\bar{2}}{\bar{14}}$ $\frac{\bar{3}}{\bar{14}}$ $\frac{\bar{4}}{\bar{14}}$ $\frac{\bar{5}}{\bar{14}}$ $\frac{\bar{6}}{\bar{14}}$ $\frac{\bar{15}}{\bar{14}}$

24. (a) P (S) = P (W1) + P (W2) +P (W3) + P (W4) +P (W5) +P (W6) +P (W7)

P (S) = 0.1 + 0.01 + 0.05 + 0.03 + 0.01 + 0.2 + 0.6

P (S) = 1

As the probability of sample space is ‘one’ the given assignment of probabilities is valid.

(b) P (S) = P (W1) + P (W2) +P (W3) + P (W4) +P (W5) +P (W6) +P (W7)

P (S) = $\frac{1}{7} + \frac{1}{7} + \frac{1}{7} + \frac{1}{7} + \frac{1}{7} + \frac{1}{7} + \frac{1}{7}$

$= \frac{1 + 1 + 1 + 1 + 1 + 1 + 1}{7} = \frac{7}{7} = 1$ .

P (S) = 1

Hence, the given assignment of probability is valid.

(c) P (S) = P (W1) + P (W2) +P (W3) + P (W4) +P (W5) +P (W6) +P (W7)

= 0.1 + 0.2 + 0.3 + 0.4 + 0.5 + 0.5 + 0.6 + 0.7

= 2.8

i.e., P (S) > 1

As probability of the sample space S should always be ‘1’. The given assignment is invalid.

(d) Here P (W1) = –0.1 is negative.

As probability of happening an event should always be positive and less than or equal to 1.

The given assignment is invalid.

(e) As P (W7) = $\frac{15}{14} = 1.07$

i.e. probability of happening an event is greater than one. The given assignment is invalid.

25. A coin is tossed twice, what is the probability that atleast one tail occurs?

25. When a coin is tossed twice we have the sample space

S = {TT, TH, HT, HH}

So, n (S) = 4

Let A be the event of getting at least one tail.

Then, A = {TH, HT, TT}

So, n (A) = 3

Therefore, P (A)= Numver of outcome favorable to A/Total possible outcomes = $\frac{}{} = \frac{n (A)}{n (S)}$ .

$= \frac{3}{4}$

34. In a lottery, a person choses six different natural numbers at random from 1 to 20, and if these six numbers match with the six numbers already fixed by the lottery committee, he wins the prize. What is the probability of winning the prize in the game? [Hint order of the numbers is not important.]

34.

. Since 6 numbers are to be choosen as fixed from a set a given 20 number, the sample space is

$n () = 20 C_{6} = \frac{20!}{6! (20 - 6)!} = \frac{20 \times 19 \times 18 \times 17 \times 16 \times 15 \times 14!}{2 \times 3 \times 4 \times 5 \times 6 \times 14!}$

$= \frac{38760}{1} \times \frac{14!}{14!} = 38760$

Let A: person wins the prize.

In order to win the prize the 6 number has to be correct i.e. all 6 of the number are to be choosen from fixed 6 numbers we have,

$n (S) =^{6}_{C6} = 1$

? P (A) = $\frac{1}{38760}$ .

40. A and B are events such that P(A) = 0.42, P(B) = 0.48 and P(A and B) = 0.16.Determine

(i) P(not A), (ii) P(not B) and (iii) P(A or B)

40. Given P (A) = 0.42

P (B) = 0.48

P (A∩B) = 0.16

(i) P (not A) = P (A') = 1 – P (A) = 1 – 0.42 = 0.58

(ii) P (not B) = P (B') = 1 – P (B) = 1 – 0.48 = 0.52

(iii) P (A or B) = P (A∪B) = P (A) + P (B) – P (A∩B)

= 0.42 + 0.48 – 0.16

= 0.74

41. In Class XI of a school 40% of the students study Mathematics and 30% study Biology. 10% of the class study both Mathematics and Biology. If a student is selected at random from the class, find the probability that he will be studying Mathematics or Biology.

41. Given that, 40% study Mathematics, 30% study Biology and 10% study both Mathematics and Biology.

Let A: Students study Mathematics.

P (A) = 40% = $\frac{40}{100}$ .

Let B: Students study Biology.

P (B) = 30% = $\frac{30}{100}$ .

So, P (A∩B) i.e. probability of student studying both Mathematics and Biology is

P (A∩B) = 10% = $\frac{10}{100}$

? P (A∪B); probability of student studying Mathematics or Biology is

P (A∪B) = P (A) + P (B) – P (A∩B)

$= \frac{40}{100} + \frac{30}{100} - \frac{10}{100}$

$= \frac{60}{100}$

$= \frac{3}{5}$ .

44. In a class of 60 students, 30 opted for NCC, 32 opted for NSS and 24 opted fo rboth NCC and NSS. If one of these students is selected at random, find the probability that

(i) The student opted for NCC or NSS.

(ii) The student has opted neither NCC nor NSS.

(iii) The student has opted NSS but not NCC.

44. Given that, total number of student, n (S) = 60

Let A: student opted for NCC

n (A) = 30

B: student opted for NSS

n (B) = 32

And student who opted both NCC and NSS, n (A∩B) = 24

(i) Probability that student opted for NCC or NSS,

P (A∪B) = P (A) + P (B) – P (A∩B)

$= \frac{n ()}{n ()} + \frac{n ()}{n ()} - \frac{n (A \capB)}{n ()}$

$= \frac{30}{60} + \frac{32}{60} - \frac{24}{60}$

$= \frac{30 + 32 - 24}{60} = \frac{38}{60} = \frac{19}{30}$

(ii) Probability that student opted neither NCC or NSS

P (not A and not B) = P (A'∩B') = P (A∪B)' = 1 – P (A∪B)

$= 1 - \frac{19}{30} = \frac{30 - 19}{30} = \frac{11}{30}$

(iii) Probabilities that student opted NSS but not NCC

P (B but not A) = P (B) – P (A∩B)

$= \frac{32}{30} - \frac{24}{30}$

$= \frac{32 - 24}{30} = \frac{8}{30} = \frac{2}{15}$

45. A box contains 10 red marbles, 20 blue marbles and 30 green marbles. 5 marbles are drawn from the box, what is the probability that

(i) All will be blue? (ii) Atleast one will be green?

45. Given,

No. of red marbles= 10

No. of blue marbles = 20

No. of green marbles = 30.

So, total no. of marbles = 10 + 20 + 30 = 60

Now, we are to select 5 marbles from the given 60 marbles.

So the sample space is:

n (s) = ⁶⁰c₅.

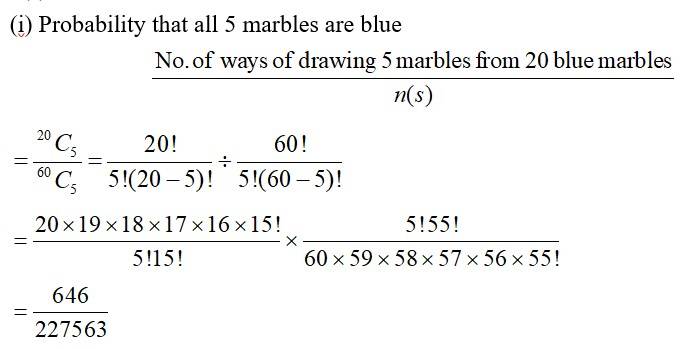
47. A die has two faces each with number ‘1’, three faces each with number ‘2’ and one face with number ‘3’. If die is rolled once, determine

(i) P(2) (ii) P(1 or 3) (iii) P(not 3)

47. Since the die has two faces each mark 1, three faces each marks 2 and one face mark 3.

The possible sample space of outcome is.

S = {1, 2, 3} so, n (s) = 6

(i) P (2) $\frac{3}{6} = \frac{1}{2}$

(ii) P (1 or 3) = P (1) + P (3) = $\frac{2}{6} + \frac{1}{6} = \frac{2 + 1}{6} = \frac{3}{6} = \frac{1}{2}$

(iii) P (not 3) = 1 P (3) = 1 - $\frac{1}{6}$ = $\frac{6 - 1}{6} = \frac{5}{6}$

48. In a certain lottery 10,000 tickets are sold and ten equal prizes are awarded. What is the probability of not getting a prize if you buy (a) One ticket (b) Two tickets (c) 10 tickets.

48. Total no. of ticket for lottery sold = 10, 000

No. of ticket that are awarded prize = 10

So, no. of ticket that are not awarded prize = 10.000 - 10

= 9990

(a) Now, probability of met getting a prize if we buy one ticket

49. Out of 100 students, two sections of 40 and 60 are formed. If you and your friendare among the 100 students, what is the probability that

(a) You both enter the same section?

(b) You both enter the different sections?

49. Here, out of 100 students, first section has 40 students and the rest I e, 60 students enters in second section.

As me and my friend are among the 100 students.

The no. of ways of selecting 2 students from the 100 students

= 100C₂

(a) When both enters first section if 2 of us are among the 40 students that are to be selected. Similarly, if both enters second section among the 60 students for that section.

(if 2 of us)

Hence, no. of ways of selecting both in same section = 40C₂ + 60C₂

Probability that both of us are in same section

50. Three letters are dictated to three persons and an envelope is addressed to each of them, the letters are inserted into the envelopes at random so that each envelope contains exactly one letter. Find the probability that at least one letter is in its proper envelope.

qqqqqqqqqqqqqqqqqqqqqqqqq

53. If 4-digit numbers greater than 5,000 are randomly formed from the digits0, 1, 3, 5, and 7, what is the probability of forming a number divisible by 5 when, (i) The digits are repeated? (ii) The repetition of digits is not allowed?

53. (a) No. of ways of forming a four-digit number greater than 5000 from the given digit 0, 1, 3, 5, 7. and digit repetition is allowed can be done in such a way either 5 or 7 and occupy the thousands' place and any of the digits 0, 1, 3, 5, 7 can occupy the remaining 3 places.

Hence, the required no. of ways = (2* 5 * 5 * 5) - 1

= 250 - 1 = 249

Here 1 is subtracted because 5000 which can be formed by the permutation of the given digits is not allowed

Hence, n (s) = 249.

Similarly, in order to formed a number divisibleby 5 we need to have either 0 or 5 in the one place.

The required number of ways = 2* 5 *5 *2 - 1

= 100 - 1

= 99.

Hence, no. of favourable went, n (E) = 99.

Probability that four digit no. greater than 5000 formed by digits 0, 1, 3, 5, 7 (when repetition is) allowed and is divisible by 5 is

P (E) = $\frac{n (E)}{n (s)} = \frac{99}{249} = \frac{33}{83}$

(B) When repetition is not allowed

We can have one of either 7 or 5 on the thousands' place. Then the remaining four other digits can occupy the hundreds, place and then the remaining 3 other digits can occupy tens' places and lastly the remaining 2 other digits can occupy the ones' place.

So, the required number of ways = 2* 4 *3* 2

n (s) = 48

Now, number of 4-digit numbers starting with 5 and divisible by 5 will have 5 on thousands' place and 0 on ones' place then the remaining 3 other digits can fill the hundreds' place and then the remaining 2 other digits can fill the tens' place. So, the required number of ways = 1 *3 *2* 1

= 6

Similarly, 4-digit number starting with 7 divisible by 5 will have 7 on the thousand's place and (one of) 0 or 5 on ones' place. Then the remaining.

3 other digits can fill the hundreds' place and then the remaining 2 other digits can fill the tens' place.

Hence the required no. of ways =1*3* 2 *2=12

So, Total no. of four digit number divisible by 5=6+12=18

Probability that four digit no. greater than 5000 formed

by digits 0,1, 3, 5, 7when repetition is not allowed and is divisible by 5 is

$\frac{18}{48} = \frac{3}{8} .$

54. The number lock of a suitcase has 4 wheels, each labelled with ten digits i.e., from 0 to 9. The lock opens with a sequence of four digits with no repeats. What is the probability of a Person getting the right sequence to open the suitcase?

54. Since, the lock can be open by a combination of four digits from the given ten digits I e, from 0 to 9. The number of ways of selecting 4 digits, = 10C₄

This combination of 4 digits can again be arranged within themselves in 41 ways. So, total number of

Class 11 Maths Probability - FAQs

These are the frequently asked questions from Probability:

Commonly asked questions

What is Probability in Class 11 Maths?

Probability in Maths is used to calculate how an event is likely to occur. It is measured by dividing the favorable outcomes number by the number of possible outcomes. It is expressed from 0% to 100% or by either 0 (impossible) or 1 (certain).

According to Class 11 Maths, what are the types of probability.

There are four types of probability - Classical, Empirical, Subjective, and Axiomatic Probability. The classical probability is based on the logical and known outcomes, Empirical are based on data from actual experiments, and subjective is based on intuition, personal opinion, or experience.

What are the basic rules of Probability in Class 11 Maths?

There are two basic rules for finding the Probability of two events A and B - Multiplication Rule and Addition Rule.

According to Class 11 Maths, which are the applications of the probability?

There are various applications of the probability in the real life. It is used to take informed decisions and risks in the following areas - insurance, weather forecasting, finance, business, sports, computer Science and gaming.

What are real world examples of the probability in Maths.

The examples of the probability include - flipping a coin, rolling a die, drawing a card from a deck, and picking a ball from a bag.