
Class 11 Mechanical Properties of Fluids talks about the physical properties of liquids and gases. It covers the similarities in liquids and gases, and the differences between fluids and solids. It provides detailed explanations of the key topics, including streamline flow, pressure, Viscosity, Bernoulli's principle, and surface tension.
Mechanical Properties of Fluids Class 11 NCERT solutions are created by the experts. The students can rely on these step-by-step solutions given by Shiksha for their CBSE Board exam and NEET, and JEE Main preparation. The Class 12 science students who are looking for a comprehensive NCERT solution on all three subjects -Physics, Chemistry, and Maths of Class 11 and Class 12, should Explore Here.
- NCERT Class 11 Physics Chapter 9 Mechanical Properties of Fluids: Weightage, Key Topics, and Important Formulas
- Class 11 Physics Mechanical properties of fluids NCERT solutions PDF: Download Free Download
- NCERT Solutions for Class 11 Physics Mechanical properties of fluids
NCERT Class 11 Physics Chapter 9 Mechanical Properties of Fluids: Weightage, Key Topics, and Important Formulas
Mechanical Properties of Fluids is a conceptual and application-based chapter in Class 11 Physics. This chapter deals with how liquids and gases behave under various forces and pressures, and understanding fluid mechanics is crucial while preparing for engineering and medical entrance exams such as NEET and JEE Main. It forms the foundation for advanced fluid dynamics, hydraulics, and biophysics topics, often appearing in numerical and reasoning-type exam questions. Check here the topics covered in Class 11 Mechanical Properties of Fluids;
| Exercise | Topics Covered |
|---|---|
| 9.1 | Introduction |
| 9.2 | Pressure |
| 9.3 | Streamline Flow |
| 9.4 | Bernoulli's Principle |
| 9.5 | Viscosity |
| 9.6 | Surface Tension |
Mechanical Properties of Fluids Weightage in NEET, JEE Main Exam
| Exam | Number of Questions |
|---|---|
| NEET | 1-2 questions |
| JEE Main | 1 question |
Related Links
| NCERT Solutions Physics Class 11th | NCERT Notes for Class 11 & 12 |
| NCERT Class 11 Notes | Class 11 Physics Notes |
Class 11 Physics Mechanical properties of fluids NCERT solutions PDF: Download Free Download
Mechanical properties of fluids Class 11 NCERT Solutions PDF helps students build a strong foundation of concepts, which is crucial in the later stages of their preparation for competitive exams. Students can download the free PDF given below.
Those who want to get access to chapter-wise important topics, weightage information, and download the free PDFs, can explore the NCERT Solutions Physics Class 11th.
Download Here: NCERT Solution for Class XI Physics Chapter Mechanical Properties of Fluids PDF
NCERT Solutions for Class 11 Physics Mechanical properties of fluids
| Q.10.2 Explain why (a) The angle of contact of mercury with glass is obtuse, while that of water with glass is acute
(b) Water on a clean glass surface tends to spread out while mercury on the same surface tends to form drops. (Put differently, water wets glass while mercury does not)
(c) Surface tension of a liquid is independent of the area of the surface
(d) Water with detergent dissolved in it should have small angles of contact
(e) A drop of liquid under no external forces is always spherical in shape |
| Ans.10.2 The angle between the tangent to the liquid surface at the point of contact and the surface inside the liquid is called the angle of contact ( , as shown in the diagram = Interfacial tension between liquid-air interface = Interfacial tension between solid -liquid interface = Interfacial tension between solid-air interface At the line of contact of contact, the surface forces between the three media must be in equilibrium. Hence = The angle of contact is obtuse, if , as in the case of mercury on glass This angle is acute if , as in the case of water on glass Mercury molecules (which makes an obtuse angle with glass) have a strong force of attraction between themselves and a weak force of attraction towards solids. Hence, they tend to form drops Water molecules make acute angles with glass. They have a weak force of attraction between themselves and a strong force of attraction towards solids. Hence, they tend to spread out Surface tension is the force acting per unit length at the interface between the plane of a liquid and any other surface. This force is independent of the area of the liquid surface. Hence, surface tension is independent of the area of the liquid surface. Water with detergent dissolved in it has a small angle of contact( This is because for a small there is a fast capillary rise of the detergent in the cloth. The capillary rise of a liquid is directly proportion to the cosine of the angle If is small, then cos will be large and then the rise of detergent in the cloth will be faster. A liquid tend to acquire the minimum surface area because of the presence of surface tension. The surface area of a sphere is the minimum for a given volume. Hence, under no external forces, liquid drops always take spherical shape. |
| Q.10.3 Fill in the blanks using the word(s) from the list appended with each statement: (a) Surface tension of liquids generally . . . with temperatures (increases / decreases)
(b) Viscosity of gases . . . with temperature, whereas viscosity of liquids . . . with temperature (increases / decreases)
(c) For solids with elastic modulus of rigidity, the shearing force is proportional to . . . , while for fluids it is proportional to. .. (shear strain / rate of shear strain)
(d) For a fluid in a steady flow, the increase in flow speed at a constriction follows (conservation of mass / Bernoulli’s principle)
(e) For the model of a plane in a wind tunnel, turbulence occurs at a ... speed for turbulence for an actual plane (greater / smaller) |
| Ans.10.3: The surface tension of a liquid is inversely proportional to temperature. Decreases Most fluids offer resistance to their motion. It is like internal mechanical friction, known as viscosity. Gas viscosity increases with temperature, whereas liquid viscosity decreases with temperature. Because, intermolecular forces weaken with temperature increase, viscosity decreases. With reference to the elastic modulus of rigidity for solids, the shearing force is proportional to the shear strain. With reference to elastic modulus of rigidity for fluids, the shearing force is proportional to the rate of shear strain. For a steady-flowing fluid, an increase in its flow speed at a constriction follows the conservation of mass (Bernouli’ principle). For the model of a plane in wind tunnel, turbulence occurs at a greater speed then it does for an actual plane. This follows from Bernoulli’s principle and different Reynolds’ numbers associated with the motions of the two planes. |
| Q.10.4 Explain why (a) To keep a piece of paper horizontal, you should blow over, not under, it
(b) When we try to close a water tap with our fingers, fast jets of water gush through the openings between our fingers
(c) The size of the needle of a syringe controls flow rate better than the thumb pressure exerted by a doctor while administering an injection
(d) A fluid flowing out of a small hole in a vessel results in a backward thrust on the vessel
(e) A spinning cricket ball in air does not follow a parabolic trajectory |
| Ans.10.4: When air is blown under a paper, the velocity of air is more than the upper portion of the paper. As per Bernoulli’s principle, atmospheric pressure reduces under the paper and makes it fall. To keep the paper horizontal, the air needs to be blown on the upper surface of the paper. For a smaller opening, the flow of fluid is more than when it is bigger. When we try to close the tap with our fingers, water gushes through the small openings. Area and velocity are inversely proportional to each other. Small opening of a syringe needle controls the velocity of the blood oozing out. At the constriction point of the syringe system, the flow rate suddenly increases to a high value for a constant thumb pressure. When a fluid flows out from a small hole in a vessel, the vessel receives backward thrust, when fluid flows out from a small hole, it attains high velocity. Due to the law of conservation of momentum, the vessel attains backward velocity. A spinning cricket ball in air has two simultaneous motions – rotary and linear. These two types of motion, opposes each other. The velocity below the ball decreases, the pressure on upper side becomes lesser than the lower side of the ball. An upward force acts on the ball and it takes a curved path, does not follow parabolic path. |
Commonly asked questions
10.19 What is the pressure inside the drop of mercury of radius 3.00 mm at room temperature? Surface tension of mercury at that temperature (20 °C) is 4.65 × 10–1 N m–1. The atmospheric pressure is 1.01 × 105 Pa. Also give the excess pressure inside the drop.
Radius of the mercury droplet, r = 3.00 mm = 3 m
Surface tension, S = 4.65 N/m
Atmospheric pressure, = 1.01 Pa
Total pressure inside the mercury drop = Excess pressure inside mercury + Atmospheric pressure
= + = + 1.01 = 1.01310 Pa
Excess pressure inside mercury = = = 310 Pa
(a) The blood pressure in humans is greater at the feet than at the brain
(b) Atmospheric pressure at a height of about 6 km decreases to nearly half of its value at the sea level, though the height of the atmosphere is more than 100 km
(c) Hydrostatic pressure is a scalar quantity even though pressure is force divided by area
The pressure of a liquid is given by the following relation:
P = h g, where P = Pressure, h = height of the liquid column, = is the density of the liquid and g= acceleration due to gravity
From the above relation, because of the h factor (height of the human body), the pressure is more at the feet and less at the brain
The said phenomenon is due to the factor. Density of air is maximum at the sea level. At height, density decreases and pressure also decreases. At 6 km height, the density of air is nearly half of that of a t sea level
When pressure is applied on the liquid, the pressure is transmitted in all directions in the liquid, Hence in absence of fixed direction, it is a scalar quantity
10.2 Explain why
(a) The angle of contact of mercury with glass is obtuse, while that of water with glass is acute
(b) Water on a clean glass surface tends to spread out while mercury on the same surface tends to form drops. (Put differently, water wets glass while mercury does not)
(c) Surface tension of a liquid is independent of the area of the surface
(d) Water with detergent dissolved in it should have small angles of contact
(e) A drop of liquid under no external forces is always spherical in shape
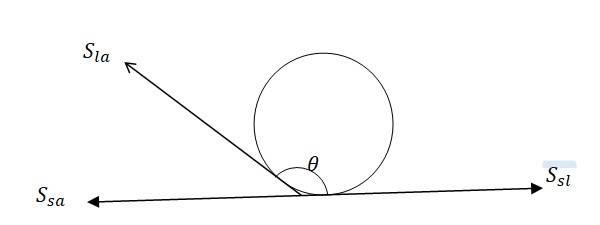
The angle between the tangent to the liquid surface at the point of contact and the surface inside the liquid is called the angle of contact ( , as shown in the diagram
= Interfacial tension between liquid-air interface
= Interfacial tension between solid -liquid interface
= Interfacial tension between solid-air interface
At the line of contact of contact, the surface forces between the three media must be in equilibrium. Hence
=
The angle of contact is obtuse, if , as in the case of mercury on glass
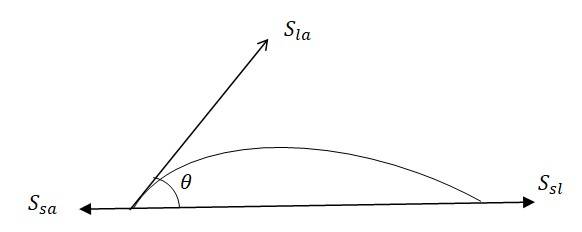
This angle is acute if , as in the case of water on glass
Mercury molecules (which makes an obtuse angle with glass) have a strong force of attraction between themselves and a weak force of attraction towards solids. Hence, they tend to form drops
Water molecules make acute angles with glass. They have a weak force of attraction between themselves and a strong force of attraction towards solids. Hence, they tend to spread out
Surface tension is the force acting per unit length at the interface between the plane of a liquid and any other surface. This force is independent of the area of the liquid surface. Hence, surface tension is independent of the area of the liquid surface.
Water with detergent dissolved in it has a small angle of contact( This is because for a small there is a fast capillary rise of the detergent in the cloth. The capillary rise of a liquid is directly proportion to the cosine of the angle If is small, then cos will be large and then the rise of detergent in the cloth will be faster.
A liquid tend to acquire the minimum surface area because of the presence of surface tension. The surface area of a sphere is the minimum for a given volume. Hence, under no external forces, liquid drops always take spherical shape.
10.9 A U-tube contains water and methylated spirit separated by mercury. The mercury columns in the two arms are in level with 10.0 cm of water in one arm and 12.5 cm of spirit in the other. What is the specific gravity of spirit?
Height of the spirit column, = 12.5 cm = 0.125 m
Height of the water column, = 10 cm = 0.1m
= atmospheric pressure
= density of spirit, = density of water
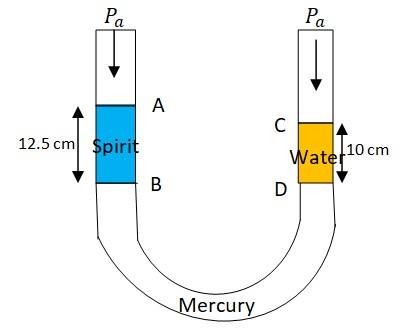
Pressure at point B = +
Pressure at point D = +
But pressure at point B and D are same. Hence
+ = + or =
= = = 0.8
So the specific gravity of spirit is 0.8
10.3 Fill in the blanks using the word(s) from the list appended with each statement:
(a) Surface tension of liquids generally . . . with temperatures (increases / decreases)
(b) Viscosity of gases . . . with temperature, whereas viscosity of liquids . . . with temperature (increases / decreases)
(c) For solids with elastic modulus of rigidity, the shearing force is proportional to . . . , while for fluids it is proportional to. .. (shear strain / rate of shear strain)
(d) For a fluid in a steady flow, the increase in flow speed at a constriction follows (conservation of mass / Bernoulli’s principle)
(e) For the model of a plane in a wind tunnel, turbulence occurs at a ... speed for turbulence for an actual plane (greater / smaller)
The surface tension of a liquid is inversely proportional to temperature. Decreases
Most fluids offer resistance to their motion. It is like internal mechanical friction, known as viscosity. Gas viscosity increases with temperature, whereas liquid viscosity decreases with temperature. Because, intermolecular forces weaken with temperature increase, viscosity decreases.
With reference to the elastic modulus of rigidity for solids, the shearing force is proportional to the shear strain. With reference to elastic modulus of rigidity for fluids, the shearing force is proportional to the rate of shear strain.
For a steady-flowing fluid, an increase in its flow speed at a constriction follows the conservation of mass (Bernouli' principle).
For the model of a plane in wind tunnel, turbulence occurs at a greater speed then it does for an actual plane. This follows from Bernoulli's principle and different Reynolds' numbers associated with the motions of the two planes.
10.4 Explain why
(a) To keep a piece of paper horizontal, you should blow over, not under, it
(b) When we try to close a water tap with our fingers, fast jets of water gush through the openings between our fingers
(c) The size of the needle of a syringe controls flow rate better than the thumb pressure exerted by a doctor while administering an injection
(d) A fluid flowing out of a small hole in a vessel results in a backward thrust on the vessel
(e) A spinning cricket ball in air does not follow a parabolic trajectory
When air is blown under a paper, the velocity of air is more than the upper portion of the paper. As per Bernoulli's principle, atmospheric pressure reduces under the paper and makes it fall. To keep the paper horizontal, the air needs to be blown on the upper surface of the paper.
For a smaller opening, the flow of fluid is more than when it is bigger. When we try to close the tap with our fingers, water gushes through the small openings. Area and velocity are inversely proportional to each other.
Small opening of a syringe needle controls the velocity of the blood oozing out. At the constriction point of the syringe system, the flow rate suddenly increases to a high value for a constant thumb pressure.
When a fluid flows out from a small hole in a vessel, the vessel receives backward thrust, when fluid flows out from a small hole, it attains high velocity. Due to the law of conservation of momentum, the vessel attains backward velocity.
A spinning cricket ball in air has two simultaneous motions – rotary and linear. These two types of motion, opposes each other. The velocity below the ball decreases, the pressure on upper side becomes lesser than the lower side of the ball. An upward force acts on the ball and it takes a curved path, does not follow parabolic path.
10.5 A 50 kg girl wearing high heel shoes balances on a single heel. The heel is circular with a diameter 1.0 cm. What is the pressure exerted by the heel on the horizontal floor?
Mass of the girl, m = 50 kg
Diameter of the heel, d = 1.0 cm = 0.01 m, Radius of the heel, r = d/2 = 0.005m
Area of the heel, = 7.85
Force exerted by heel on the floor, F = mg = 50 N = 490 N
Pressure exerted by heel on the ground, p = F/A = 490/ (7.85 N/
= 6.24 N/
10.6 Torricelli’s barometer used mercury. Pascal duplicated it using French wine of density 984 kg m–3. Determine the height of the wine column for normal atmospheric pressure.
Density of mercury, = 13.6 kg/
Density of wine, = 9.84 kg/
Height of the mercury column for atmospheric pressure, = 760 mm = 0.76 m
Height of the mercury column for atmospheric pressure =
From the relation, P = , since the pressure on both the system are equal
= , we get = = = 10.5 m
10.7 A vertical off-shore structure is built to withstand a maximum stress of 109 Pa. Is the structure suitable for putting up on top of an oil well in the ocean? Take the depth of the ocean to be roughly 3 km, and ignore ocean currents.
The maximum allowable stress for the structure, P = Pa
Depth of the ocean, d = 3 km = 3 m
Density of water = kg/
Acceleration due to gravity, g = 9.8 m/s
The pressure exerted because of sea water at the depth d = = 3 Pa
= 2.94 Pa
The maximum allowable stress is more than the pressure, hence the structure is suitable.
10.8 A hydraulic automobile lift is designed to lift cars with a maximum mass of 3000 kg. The area of cross-section of the piston carrying the load is 425 cm2. What maximum pressure would the smaller piston have to bear?
The maximum mass of the car can be lifted, m = 3000 kg
Area of cross-section of the load carrying piston, A = 425 = 425
Maximum force exerted by the load, F = mg = 3000 N = 29400 N
Maximum pressure exerted, P = F/A = (29400 / 425 ) Pa = 6.917 Pa
10.10 In the previous problem, if 15.0 cm of water and spirit each are further poured into the respective arms of the tube, what is the difference in the levels of mercury in the two arms? (Specific gravity of mercury = 13.6)
Height of the spirit column, = 12.5 + 15 cm = 27.5 cm
Height of the water column, = 10 + 15 cm = 25 cm
Density of spirit, = 0.8 gm/
Density of water, = 1 gm/
Density of mercury, = 13.6 gm/
Let h be the difference between the levels of mercury in two limbs
Pressure exerted by mercury column of h height= h = 13.6hg …. (i)
Difference between pressure exerted by water and spirit columns:
= 3g ……. (ii)
Equating equations (i) and (ii), we get
13.6hg = 3g
h = 3/13.6 = 0.221 cm
10.11 Can Bernoulli’s equation be used to describe the flow of water through a rapid in a river? Explain.
No, Bernoulli's equation cannot be used to describe the flow of water through a rapid in a river. In rapid, the flow is turbulent whereas Bernoulli's equation is applicable for laminar flow only.
10.12 Does it matter if one uses gauge instead of absolute pressures in applying Bernoulli’s equation? Explain.
It does not matter if one uses gauge pressure, instead of absolute pressure while applying Bernoulli's equation. There should be significantly different atmospheric pressures, where Bernoulli's equation is applied.
10.13 Glycerin flows steadily through a horizontal tube of length 1.5 m and radius 1.0 cm. If the amount of glycerin collected per second at one end is 4.0 × 10–3 kg s–1, what is the pressure difference between the two ends of the tube? (Density of glycerin = 1.3 × 103 kg m–3 and viscosity of glycerin = 0.83 Pa s). [You may also like to check if the assumption of laminar flow in the tube is correct].
Length of the horizontal tube, l = 1.5 m
Radius of the tube, r = 1 cm = 0.01 m
Diameter of the tube, d = 2r = 0.02m
Glycerine mass flow rate, M = 4 kg/s
Density of glycerine, = 1.3 kg
Viscosity of glycerine, = 0.83 Pa-s
Now, volume of glycerine flowing per sec V = = /s = 3.08 /s
According to Poiseville’s formula, we know the flow rate
V = where p is the pressure difference between two ends of the tube
p = = = 976.47 Pa
Reynolds’s number is given by the relation
Re = = = 0.3
Since the Reynolds’s number is 0.3, the flow is laminar
10.14 In a test experiment on a model aeroplane in a wind tunnel, the flow speeds on the upper and lower surfaces of the wing are 70 m s–1and 63 m s-1 respectively. What is the lift on the wing if its area is 2.5 m2? Take the density of air to be 1.3 kg m–3.
Speed of the wind on the upper surface of the wing, = 70 m/s
Speed of the wind on the lower surface of the wing, = 63 m/s
Area of the wing, A = 2.5
Density of air, = 1.3 kg/
According to Bernoulli’s theorem, we have the relation:
+ = +
( - )= - , where = pressure on the upper surface of the wing and - pressure on the lower surface of the wing
The pressure difference provides lift to the aeroplane
Lift on the wing = ( - )A = - A = - N = 1512.8 N = 1.5 N
10.15 Figures 10.23(a) and (b) refer to the steady flow of a (non-viscous) liquid. Which of the two figures is incorrect ? Why ?
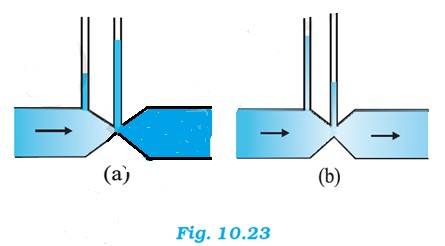
Take the case given in figure (b)
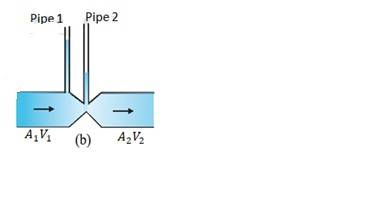
= Area of pipe 1, = Area of pipe 2, = Speed of fluid in pipe 1, = Speed of fluid in pipe 2
From the law of continuity, we have
=
When the area of cross-section in the middle of the venturimeter is small, the speed of the flow of liquid through this part is more. According to Bernoulli's principle, if speed is more, the pressure is less. Pressure is directly proportional to height, hence the level of water in pipe 2 is less. Therefore, figure (a) is not possible.
10.16 The cylindrical tube of a spray pump has a cross-section of 8.0 cm2 one end of which has 40 fine holes each of diameter 1.0 mm. If the liquid flow inside the tube is 1.5 m min–1, what is the speed of ejection of the liquid through the holes?
Area of cross-section of the spray pump, = 8 = 8
Number of holes, n = 40
Diameter of each hole, d = 1 mm = 1 m
Radius of each hole, r = d/2 = 0.5 m
Area of cross-section of each hole, a = =
Total area of 40 holes, = 40 = 3.14
Speed of liquid inside the tube, = 1.5 m/min = 0.025 m/s
Speed of ejection of liquid =
According to law of continuity, we have = or =
= 0.637 m/s
10.17 A U-shaped wire is dipped in a soap solution, and removed. The thin soap film formed between the wire and the light slider supports a weight of 1.5 × 10–2 N (which includes the small weight of the slider). The length of the slider is 30 cm. What is the surface tension of the film?
The weight that the soap film supports, W = 1.5 N
Length of the slider, l = 30 cm = 0.3 m
A soap film has two free surfaces, hence total length = 2l = 0.6 m
Surface tension, S= = = 2.5 N/m
10.18 Figure 10.24 (a) shows a thin liquid film supporting a small weight = 4.5 × 10–2 N. What is the weight supported by a film of the same liquid at the same temperature in Fig. (b) and (c)? Explain your answer physically.
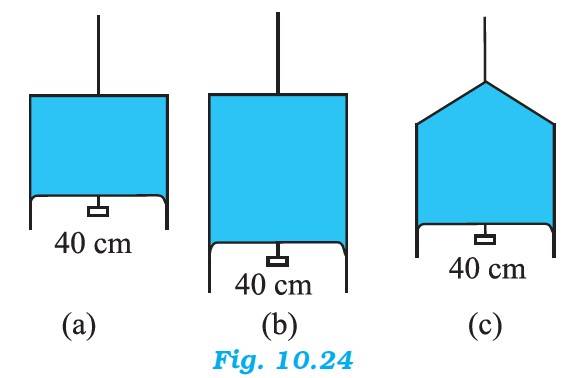
The length of the liquid film supported by the weight, l = 40 cm = 0.4 m
The weight supported by the film, W = 4.5 N
Since a liquid film has two free surfaces,
Surface tension = = = 5.625 N/m
In all 3 figures, the liquid is the same, temperature is also the same. Hence the surface tension in (b) and (c) are also going to be the same, with the value of 5.625 N/m and weight supported in each case is also going to be the same, since length of the film is same.
10.20 What is the excess pressure inside a bubble of soap solution of radius 5.00 mm, given that the surface tension of soap solution at the temperature (20 °C) is 2.50 × 10–2 N m–1 ? If an air bubble of the same dimension were formed at depth of 40.0 cm inside a container containing the soap solution (of relative density 1.20), what would be the pressure inside the bubble ? (1 atmospheric pressure is 1.01 × 105 Pa).
Soap bubble radius, r = 5.0 mm = 5 m
Surface tension of the soap bubble, S = 2.50 N/m
Relative density of soap solution = 1.20, hence density of soap solution, = 1.2 Kg/
Air bubble formed at a depth, h = 40 cm = 0.4 m
1 atmospheric pressure = 1.01 Pa
Acceleration due to gravity, g = 9.8 m/
We know, the excess pressure inside the soap bubble is given by the relation:
P = = Pa = 20 Pa
Hence, the excess pressure inside the air bubble is given by the relation, P' = = 10 Pa
At a depth of h, the total pressure inside the air bubble = Atmospheric pressure + h g +P'
= 1.01 + (0.4 + 10 Pa = 105714 Pa = 1.06 Pa
10.21 A tank with a square base of area 1.0 m2 is divided by a vertical partition in the middle. The bottom of the partition has a small-hinged door of area 20 cm2. The tank is filled with water in one compartment, and an acid (of relative density 1.7) in the other, both to a height of 4.0 m. compute the force necessary to keep the door close.
Base area of the given tank, A = 1.0
Area of the hinged door, a = 20 = 20
Density of water, = kg/
Density of acid, = 1.7 kg/
Height of the water column, = 4 m
Height of the acid column, = 4 m
Acceleration due to gravity, g = 9.8 m/
The pressure due to Water column, = = = 3.92 Pa
The pressure due to Acid column, = = 1.7 = 6.64 Pa
Pressure difference between two columns ΔP = - = 2.774 Pa
Force exerted on the small hinged door = ΔP = 2.774 20 N = 55.48 N
10.22 A manometer reads the pressure of a gas in an enclosure as shown in Fig. 10.25 (a) When a pump removes some of the gas, the manometer reads as in Fig. 10.25 (b) .The liquid used in the manometers is mercury and the atmospheric pressure is 76 cm of mercury.
(a) Give the absolute and gauge pressure of the gas in the enclosure for cases (a) and (b), in units of cm of mercury
(b) How would the levels change in case (b) if 13.6 cm of water (immiscible with mercury) are poured into the right limb of the manometer? (Ignore the small change in the volume of the gas)
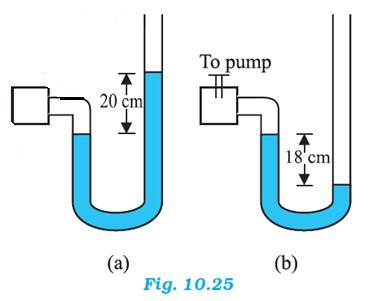
Atmospheric pressure, = 76 cm of Hg
For figure (a)
Difference between the levels of mercury in the two limbs gives gauge pressure
Hence, gauge pressure = 20 cm of Hg
Absolute pressure = Atmospheric pressure + Gauge pressure = 76 + 20 = 96 cm of Hg
For figure (b),
Difference between the levels of mercury in the two limbs gives gauge pressure
Hence, gauge pressure = - 18 cm of Hg
Absolute pressure = Atmospheric pressure + Gauge pressure = 76 - 18 = 58 cm of Hg
When 13.6 cm of water is poured into the right limb of figure (b)
Relative density of mercury = 13.6
Hence, a column of 13.6 cm of water is equivalent to 1 cm of Mercury.
Let h be the difference between the levels of mercury in the two limbs
The pressure in the right limb is given as:
= Atmospheric pressure + 1 cm of Hg = 76 + 1 = 77 cm of Hg
The mercury column will rise in the left limb. Hence, pressure in the left limb
= 58 + h
Since = , we get h = 77 – 58 = 19 cm
10.23 Two vessels have the same base area but different shapes. The first vessel takes twice the volume of water that the second vessel requires to fill up to a particular common height. Is the force exerted by the water on the base of the vessel the same in the two cases? If so, why do the vessels filled with water to that same height give different readings on a weighing scale?
Two vessels, having the same base area, will have identical force and equal pressure acting on their common base area. Since the shapes of the two vessels are different, the force exerted on the sides of the vessels has non-zero vertical components.
When these vertical components are added, the total force on one vessel comes out to be more than on the other vessel. Hence, when these vessels are filled with water to the same height, they give different readings on the weighing scale.
10.24 During blood transfusion the needle is inserted in a vein where the gauge pressure is 2000 Pa. At what height must the blood container be placed so that blood may just enter the vein? [Use the density of whole blood from Table 10.1].
Gauge pressure, P = 2000 Pa
Density of whole blood, = 1.06 kg/
Acceleration due to gravity, g = 9.8 m/s
Let the height of the blood container = h
Pressure on the blood container P =
By equating, we get h = (2000)/ ( 1.06 = 0.1925m
10.25 In deriving Bernoulli’s equation, we equated the work done on the fluid in the tube to its change in the potential and kinetic energy. (a) What is the largest average velocity of blood flow in an artery of diameter 2 × 10–3 m if the flow must remain laminar? (b) Do the dissipative forces become more important as the fluid velocity increases? Discuss qualitatively.
Diameter of the artery, d = 2 m
Viscosity of the blood, = 2.084 Pa-s
Density of the blood, = 1.06 kg/
Reynolds’s number for laminar flow, = 2000
= = = 1.966 m/s
As the fluid velocity increases, the dissipative forces become more important. This is because of the rise of turbulence. Turbulent flow causes dissipative loss in a fluid.
10.26 (a) What is the largest average velocity of blood flow in an artery of radius 2×10–3m if the flow must remain laminar? (b) What is the corresponding flow rate? (Take viscosity of blood to be 2.084 × 10–3 Pa s).
Radius of the artery, r = 2 m
Diameter of the artery, d = 4 m
Viscosity of blood, = 2.084 Pa-s
Density of the blood, = 1.06 kg/
Reynolds’s number for laminar flow, = 2000
The largest velocity is given by the relation: =
= = 0.983 m/s
Flow rate is given by the relation:
R = = 3.1416 = 1.235 /s
10.27 A plane is in level flight at constant speed and each of its two wings has an area of 25 m2. If the speed of the air is 180 km/h over the lower wing and 234 km/h over the upper wing surface, determine the plane’s mass. (Take air density to be 1 kg m–3).
The area of the wing of the plane, A = 2 = 50
Speed of air over the lower wing, = 180 km/h = 50 m/s
Speed of air over the upper wing, = 234 km/h = 65 m/s
Density of air, = 1 kg/
Let us assume, pressure over the lower wing = and pressure over the upper wing =
The upward force on the plane can be obtained using Bernoulli’s equation:
On lower wing= + , On upper wing = +
From equilibrium of momentum
+ = +
( - )
The net upward force = ( - = )
= ) = 43125 N
Using the relation F = mg, we get m = F/g
= (43125/9.8) Kg = 4400.51 kg
Hence the mass of the plane is about 4400 kg.
10.28 In Millikan’s oil drop experiment, what is the terminal speed of an uncharged drop of radius 2.0 × 10–5 m and density 1.2 × 103 kg m–3. Take the viscosity of air at the temperature of the experiment to be 1.8 × 10–5 Pa s. How much is the viscous force on the drop at that speed ? Neglect buoyancy of the drop due to air.
Radius of the uncharged drop, r = 2.0 m
Density of the uncharged drop, = 1.2 kg/
Viscosity of air, = 1.8 Pas
Density of air , can be taken as zero in order to neglect the buoyancy of air
Acceleration due to gravity, g = 9.8 m/
Terminal velocity, v can be written as
v = = = 0.05807 m/s = 5.8 cm/s
The viscous force on the drop is given by
F = 6 = 6 1.8 2.0 0.05807
= 3.9 N
10.29 Mercury has an angle of contact equal to 140° with soda lime glass. A narrow tube of radius 1.00 mm made of this glass is dipped in a trough containing mercury. By what amount does the mercury dip down in the tube relative to the liquid surface outside? Surface tension of mercury at the temperature of the experiment is 0.465 N m–1. Density of mercury = 13.6 × 103 kg m–3.
Radius of the narrow tube, r = 1 mm= 1 m
Surface tension of mercury at the given temperature, s= 0.465 N/m
Density of mercury kg/
Dipping depth = h
Acceleration due to gravity, g = 9.8 m/
Surface tension related with angle of contact and dipping depth is given by:
s = or h = = = -5.345 m= -5.345 mm
10.30 Two narrow bores of diameters 3.0 mm and 6.0 mm are joined together to form a U-tube open at both ends. If the U-tube contains water, what is the difference in its levels in the two limbs of the tube? Surface tension of water at the temperature of the experiment is 7.3 × 10–2 N m–1. Take the angle of contact to be zero and density of water to be 1.0 × 103 kg m–3 (g = 9.8 m s–2)
Diameter of the 1st bore, = 3 mm = 3 m
Radius of the first bore, = 1.5 mm = 1.5 m
Diameter of the 2nd bore, = 6 mm = 6 m
Radius of the 2nd bore, = 3.0 mm = 3 m
Surface tension of water, s= 7.3 N/m
Angle of contact between the bore surface and water,
Density of water, kg/
Acceleration due to gravity. g = 9.8 m/
Let and be the heights to which water rises in 1st and 2nd tubes respectively. These heights are given by the relations:
…(i)
…(ii)
The difference in level of water in the 2 limbs
= ( -
= ( - = 4.965 m = 4.965 mm
10.31 (a) It is known that density of air decreases with height y as
where = 1.25 kg m–3 is the density at sea level, and is a constant. This density variation is called the law of atmospheres. Obtain this law assuming that the temperature of atmosphere remains a constant (isothermal conditions). Also assume that the value of g remains constant.
(b) A large He balloon of volume 1425 m3 is used to lift a payload of 400 kg. Assume that the balloon maintains constant radius as it rises. How high does it rise?
[Take = 8000 m and = 0.18 kg m–3].
Volume of the balloon, V = 1425
Mass of the payload, m = 400 kg
Acceleration due to gravity, g = 9.8 m/
= 8000 m
= 0.18 kg m–3
= 1.25 kg m–3
Density of the balloon =
Height to which the balloon will rise = y
Density of air decreases with height and the relationship is given by:
= ……(i)
Differentiating equation (i), we get
, where k is the constant of proportionality
, height changes from 0 to y, while density changes from to . Integrating both sides between the limits, we get:
= -ky
= ….(ii)
From equation (i) and (ii), we get
= , k =
Substituting the value of k in equation (ii), we get
Density =
= = 0.461 kg/
From equation (iii), taking log on both sides
= -
y = -8000 = 8000 m = 8 km
The balloon will rise to 8 km
Explore exams which ask questions on physics ncert solutions class 11th
Select your preferred stream
physics ncert solutions class 11th Exam
Student Forum
Other Similar chapters for you
- Physical World
- Units and Measurements
- Motion in a Straight Line
- Motion in a Plane
- Laws of Motion
- Work, Energy, and Power
- System of Particles and Rotational Motion
- Gravitation
- Mechanical Properties of Solids
- Mechanical Properties of Fluids
- Thermal Properties of Matter
- Thermodynamics
- Kinetic Theory
- Oscillations
- Waves
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test
