Multiplication of Vectors by Real Numbers (Scalar Multiplication): Definition, Properties, and More

Multiplication of a vector by a real number or scalar multiplication is a straightforward operation that modifies or scales a vector by a real number. This affects its length or reverses its direction. 

At this time, it’s important to go back to differences between scalar and vector quantities. Because you will start understanding motion in two or three dimensions, when positive and negative signs don’t fully give the picture of direction. In one dimension, a negative sign was enough to indicate "backward" or "opposite direction."

Scalar multiplication gives us the mathematical tool to scale any vector quantity. This operation preserves its directional relationship to the original vector.

Simple Explanation and Representation of Scalar Multiplication

When we multiply a vector by a real number (scalar), the magnitude of the vector changes. 

But its direction either remains the same or reverses (depending on the sign of the scalar).

A basic example to represent a scalar multiplication to take note of is,
For vector A and scalar k, when we multiply, we get

• kA is a new vector with magnitude |k| × |A|
• The direction depends on the sign of k.

 

Vector multiplication by a real number is not simply numeric in its result. This kind of vector operation is always structure-preserving. That’s a key tenet of vector algebra that makes it behave in a predictable way. 

These properties of scalar multiplication are exactly part of what defines a real vector space.

1. Distributive over Vector Addition (stretch after combining)

When you first add two vectors 𝐀 and 𝐁, and then scale the result by k, it's the same as scaling each vector first and then adding

$k(\vec{A}+\vec{B})=k\vec{A}+k\vec{B}$

2. Distributive over Scalar Addition (composing scalings)

Scaling by k + m is the same as scaling by k and by m separately, then adding.

$(k+m)\vec{A}=k\vec{A}+m\vec{A}$

3. Compatibility of Nested Scalings 

If you scale 𝐀 by m, then scale the result by k, it’s the same as scaling once by (k·m). It's an associative property

$k\left(m\vec{A}\right)=\left(km\right)\vec{A}$

4. Scalar Identity

Multiplying by 1 leaves the vector unchanged. This is obvious but essential. It's part of the behaviour defined in all vector spaces. 

$1\cdot \vec{A}=\vec{A}$

5. Zero Scalar Law

Scaling by zero always gives the zero vector. It does not depend on what 𝐀 is.

0⋅A=0

 

6. Scalar Inverse (Negation)

Scaling by −1 flips the vector in the opposite direction. So, −𝐀 is precisely the vector with the same length but reversed orientation.

(−1)⋅A=−A

 

Let’s look at an example of scalar multiplication. 

For a vector $\vec{A}=A_x\hat{i}+A_y\hat{j}$  and a real number $k$ , the product is $k\vec{A}=\left(k{A}_x\right)\hat{i}+$ $\left(k{A}_y\right)\hat{j}$ . The magnitude of $k\vec{A}$  is $\left|k\right|\left|\vec{A}\right|$ , and the direction remains the same if $k>0$ or reverses if $k<0$

Implications of the Example

• Scalar multiplication affects all components proportionally.
• If $k=0$ , the result is the zero vector $\vec{0}$ .
• Unit vectors scale to $k\hat{i},k\hat{j}$ .

 

Scalar multiplication is used to scale physical quantities like velocity, acceleration, and force in multi-dimensional motion. The main applications include the following.  

• Projectile Motion: Scaling initial velocity components, e.g., $\vec{u}=u\mathrm{c}\mathrm{o}\mathrm{s}\theta \hat{i}+u\mathrm{s}\mathrm{i}\mathrm{n}\theta \hat{j}$ , where trigonometric factors scale components.  
• Relative Motion: Scaling velocities, e.g., ${\vec{v}}_{AB}=k{\vec{v}}_A$ in river-boat problems.
• Force Analysis: Scaling forces, as per the Second Law of Newton, $\vec{F}=m\vec{a}$ , where $m$ is a scalar, while acceleration is a vector. 

Let's look into some common questions you can expect in JEE Main or similar. 

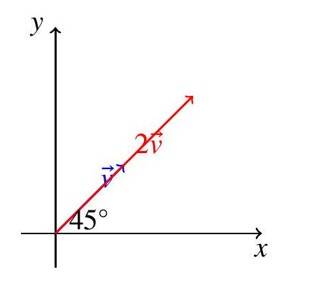
Example 1: A velocity vector $\vec{v}=10\hat{i}+10\hat{j}\mathrm{m}/\mathrm{s}$  is scaled by a factor of 2 . Find the resulting vector and its magnitude. - Solution:

$2\vec{v}=2(10\hat{i}+10\hat{j})=20\hat{i}+20\hat{j}\mathrm{m}/\mathrm{s}$

Magnitude: $\left|2\vec{v}\right|=\sqrt[]{{20}^2+{20}^2}=\sqrt[]{800}=20\sqrt[]{2}\approx 28.3\mathrm{m}/\mathrm{s}$ .

Diagram:

Diagram Description: The diagram shows $\vec{v}$  (blue) at ${45}^{\circ }$  with components $10\hat{i}+10\hat{j}$ . The scaled vector $2\vec{v}$  (red) is twice as long, maintaining the same direction.

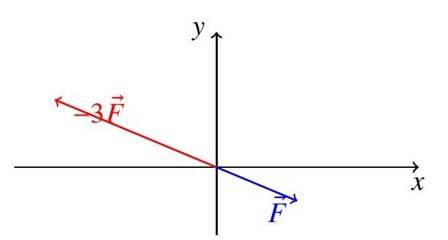
Example 2: A force $\vec{F}=12\hat{i}-5\hat{j}\mathrm{N}$  is multiplied by -3 . Find the resulting vector and its direction.

Solution:

$-3\vec{F}=-3(12\hat{i}-5\hat{j})=-36\hat{i}+15\hat{j}\mathrm{N}$

Magnitude: $|-3\vec{F}|=\sqrt[]{(-36{)}^2+{15}^2}=\sqrt[]{1296+225}=\sqrt[]{1521}=39$  N. Direction: $\mathrm{t}\mathrm{a}\mathrm{n}\theta =$ $\frac{15}{-36}=-\frac{5}{12}$ , so $\theta \approx {180}^{\circ }-{\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left(\frac{5}{12}\right)\approx {157.4}^{\circ }$  from positive $x$ -axis.

Diagram:

Diagram Description: The diagram shows $\vec{F}$ (blue) in the fourth quadrant. The scaled vector $-3\vec{F}$ (red) is three times longer and reversed, lying in the second quadrant.

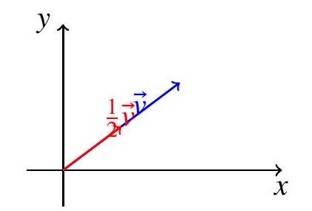
Example 3: A velocity $\vec{v}=8\hat{i}+6\hat{j}\mathrm{m}/\mathrm{s}$  is scaled by $\frac{1}{2}$ . Find the resulting vector and verify the distributive property with another vector $\vec{u}=4\hat{i}-2\hat{j}\mathrm{m}/\mathrm{s}.-\mathrm{*}\mathrm{*}$  Solution:**

$\frac{1}{2}\vec{v}=\frac{1}{2}(8\hat{i}+6\hat{j})=4\hat{i}+3\hat{j}\mathrm{m}/\mathrm{s}$

Magnitude: $\left|\frac{1}{2}\vec{v}\right|=\sqrt[]{4^2+3^2}=\sqrt[]{25}=5\mathrm{m}/\mathrm{s}$ . Verify distributive property: $\frac{1}{2}(\vec{v}+\vec{u})=\frac{1}{2}\vec{v}+\frac{1}{2}\vec{u}$ . Left: $\vec{v}+\vec{u}=(8+4)\hat{i}+(6-2)\hat{j}=12\hat{i}+4\hat{j}$ , so $\frac{1}{2}(12\hat{i}+4\hat{j})=6\hat{i}+2\hat{j}$ . Right: $\frac{1}{2}\vec{v}=4\hat{i}+3\hat{j}$ , $\frac{1}{2}\vec{u}=\frac{1}{2}(4\hat{i}-2\hat{j})=2\hat{i}-\hat{j}$ , so $(4\hat{i}+3\hat{j})+(2\hat{i}-\hat{j})=6\hat{i}+2\hat{j}$ . Both match.

Diagram:

Diagram Description: The diagram shows $\vec{v}$ (blue) with components $8\hat{i}+6\hat{j}$ . The scaled vector $\frac{1}{2}\vec{v}$ (red) is half as long, maintaining the same direction.

Check these links for revising before exams. Find topic wise guides for each chapter. 

Units and Measurements Class 11 Notes	Mechanical Properties of Solids Class 11 Notes
Motion in a Straight Line Class 11 Notes	Mechanical Properties of Fluids Class 11 Notes
NCERT Class 11 Notes for Motion in a Plane	Thermal Properties of Matter Class 11 Notes
Laws of Motion Class 11 Notes	Thermodynamics Class 11 Notes
Work, Energy, and Power Class 11 Notes	Kinetic Theory of Gas Class 11 Notes
System of Particles and Rotational Motion Class 11 Notes	Oscillations Class 11 Notes
Gravitation Class 11 Notes	Waves Class 11 Notes

Get an overview of all Science stream notes for Class 11 CBSE

NCERT Class 11 Notes for PCM

NCERT Class 11 Physics Notes