Before learning about projectile motion, it is essential to identify what a projectile is and how gravity is a contributing factor. It is equally important to understand the differences between scalars and vectors when studying motion and direction. While you learn all this in the chapter, Motion in a Plane, which roughly talks about motion in the two-dimensional space, there is more to uncover.
Starting with the definition of a projectile, which is an object launched into the air, moving under the force of gravity alone. This movement in physics is projectile motion. But, to inquisitive and studious minds like yours, you may be concerned about acceleration, the direction and angle of the path, and different scenarios where the projectile moves. We cover all this here.
- What is Projectile Motion?
- NCERT Definition of Projectile Motion
- Galileo's Statement
- Projectile Thrown at an Angle with Horizontal
- Equation of Trajectory
- Projection Thrown Parallel to the Horizontal from some Height
- Time of flight
- Horizontal range
- Velocity at a general point P (x ,y)
- Velocity with which the projectile hits the ground
- Trajectory equation
What is Projectile Motion?
The movement of a projectile in air, acted upon by gravity as the only force, is known as projectile motion. As an example of two-dimensional motion where acceleration is constant, it combines two simultaneous motions that are mutually perpendicular and independent of each other.
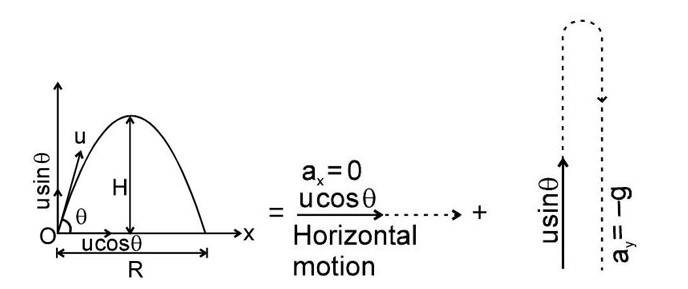
In a graph, you will see horizontal and vertical motion when trying to decipher projectile motion.
Horizontal motion alone = straight line sideways
Vertical motion alone = straight line up and down
Horizontal motion + Vertical motion = Parabolic path (the curved trajectory)
NCERT Definition of Projectile Motion
The NCERT book describes projectile motion as
"An object that is in flight after being thrown or projected is called a projectile. Such a projectile might be a football, a cricket ball, a baseball or any other object. The motion of a projectile may be thought of as the result of two separate, simultaneously occurring components of motions. One component is along a horizontal direction without any acceleration and the other along the vertical direction with constant acceleration due to the force of gravity."
Galileo's Statement
Galileo stated in his Dialogue on the Great World Systems, 1632, that two perpendicular directions of motion are always independent of each other. So in physics, the vector quantity directed along a direction will not be affected by a vector perpendicular to it.
Projectile Thrown at an Angle with Horizontal
- Let's say a projectile that is thrown with a velocity u is making an angle theta with the horizontal.
- The initial velocity gets resolved into components within a coordinate system. The horizontal direction, then, is taken as x-axis, while vertical direction as y-axis and point of projection as the origin.
- We can also consider this projectile motion as the combination of horizontal and vertical motion. So, Horizontal direction and Vertical Direction can be seen as
(a) Initial velocity for horizontal
Initial velocity for vertical
(b) Acceleration for horizonal
Acceleration for vertical
(c) Velocity after time for horizontal
Velocity after time for vertical
Time of Flight
The displacement then along the vertical direction will be zero for the entire flight.
Hence, along vertical direction net displacement
Horizontal Range
Maximum Height
The trajectory's highest point sees the object moving in horizontal direction, so the vertical component of velocity will be zero.
Using equation of motion i.e. as we have for vertical direction
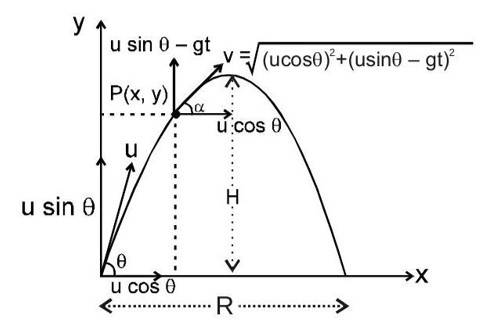
Resultant Velocity
Where,
and
.
Also,
General Result
1. For maximum range
2. We find the same range for two projection angles
and (
). However, in these two cases, the maximum height the particles go up to would be different.
This is because,
, and
3. If
i.e.
4. We can also express range as
Equation of Trajectory
The path a particle or projectile follows during motion is its Trajectory. So the equation of trajectory is the relation between instantaneous coordinates (x and y), of the particle. When we consider the horizontal direction,
For vertical direction :
Eliminating ' t ' from equation (1) & (2)
This is the parabola equation and is known as the trajectory equation of projectile motion.
Here are some other forms of the trajectory/parabola equation.
ey
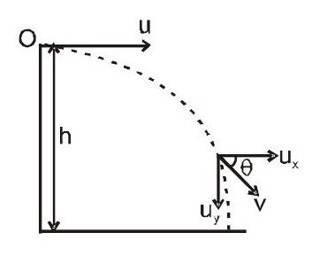
Projection Thrown Parallel to the Horizontal from some Height
Consider a projectile thrown from point O at some height from the ground with a velocity u. Let's review projectile motion's characteristics, only by resolving motion along both directions: horizontal and vertical.
Horizontal direction
(i) Initial velocity
(ii) Acceleration
Vertical direction
(i) Initial velocity
(ii) Acceleration (downward)
Time of flight
Here, it is equal to the time the projectile takes to return to the ground. So, from the equation of motion , alongside the vertical direction, we get
Horizontal range
Velocity at a general point P (x ,y)
Velocity with which the projectile hits the ground
Trajectory equation
Physics Motion in Plane Exam
Student Forum
Other Class 11th Physics Chapters
- Physics Mechanical Properties of Solids
- NCERT Class 11 Physics
- NCERT Class 11 Notes
- NCERT Notes
- Physics Motion in Plane
- Physics Mechanical Properties of Fluids
- Physics Motion in Straight Line
- Physics System of Particles and Rotational Motion
- Physics Oscillations
- Physics Waves
- Physics Thermal Properties of Matter
- Physics Motion
- Physics Gravitation
- Physics Thermodynamics
- Physics Work, Energy and Power
- Physics Units and Measurement
- Physics Laws of Motion