Let's quickly advance with the chapter on Motion in a Plane in Class 11 Physics with vector addition and subtraction using the graphical method.
So far in Class 11 Physics, you have a good idea of how vectors differ from scalar quantities with an added element of direction with magnitude. Likewise, the ordinary algebraic rules that you have already learnt to apply to scalars will not work with vectors. Vectors obey specific rules, particularly the law of parallelogram. Beyond that, you have to know what visually happens when we add or subtract vectors. Learning these mathematical operations properly will help forever, especially if you are deciding to get into engineering and/or physics, where it will be the part and parcel of analysing velocities, displacements, and types of forces in the real-world.
We will cover these mathematical operations that have specific graphical representations, along with important laws and properties, here today.
- Vector Meaning and Types
- Vector Addition and Subtraction Rules
- Vector Addition by Graphical Method
- Vector Subtraction by Graphical Method
- Applications of Addition and Subtraction of Vectors in Physics
- JEE-Level Examples of Addition and Subtraction of Vectors
- Class 11 Physics Notes for Quick Revisions Before Exams
- NCERT Solutions for Class 11 Physics Simplified
Vector Meaning and Types
Before moving on to the graphical representations of vector addition and subtraction, let's review the definition and types.
Definition of Vectors
We can define vectors by two characteristics.
- Magnitude - The size or length of the vector, which is always positive.
- Direction - The orientation of the vector in space (or coordinates in 2D and 3D spaces), which we represent using angles and unit vectors.
Types of Vectors
- Resultant Vector - This is a single vector that shows the combined effect of two or more vectors.
- Unit Vector - This is a vector with magnitude equal to 1. This is used to specify direction in space. We usually represent unit vectors as
- Zero/Null Vector - A vector with zero magnitude. Even the direction is undefined. A simple example is when the initial and final positions coincide. In this case, the displacement is a null vector.
Vector Addition and Subtraction Rules
Vector addition combines two or more vectors to produce a resultant vector. This mathematical operation can be represented graphically by two methods.
One is the parallelogram law, and the other is the triangle law.
Parallelogram Law of Vector Addition and Subtraction
The law of parallelogram states that when we add two adjacent sides of a parallelogram, the resultant vector is the diagonal of the parallelogram. This resultant vector originates from the same point where the two adjacent sides meet.
Triangle Law of Vector Addition and Subtraction
The triangle law applies to the two adjacent sides of a triangle, where the resultant vector originates from the same point as the intersecting point.
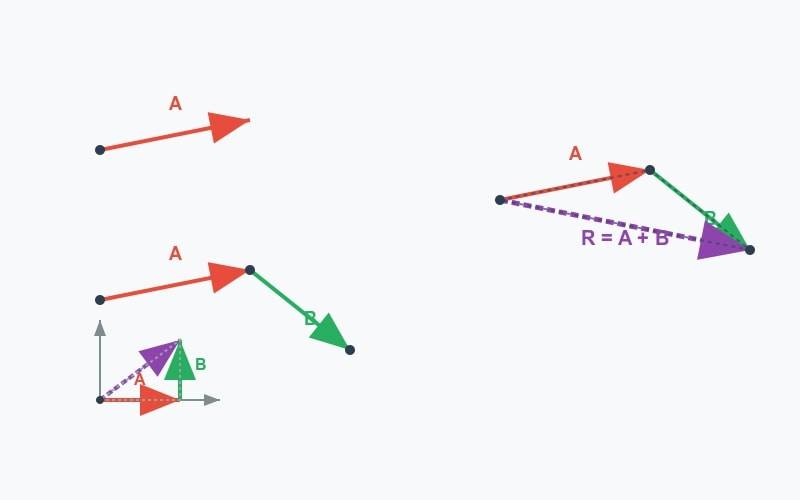
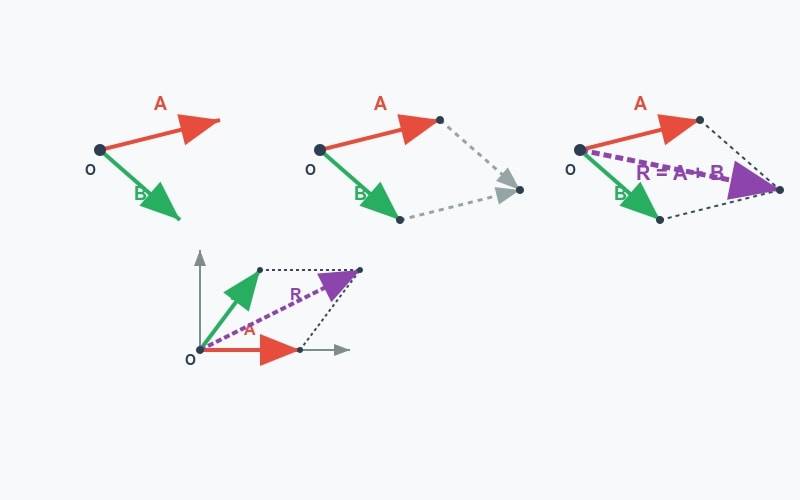
Vector Addition by Graphical Method
Let's see how we can graphically represent vector addition using the two laws we learnt above.
Graphical Representations of Vector Addition using Parallelogram and Triangle Laws
Let’s consider two vectors, and .
We will see how the triangle and parallelogram laws apply in this context.
- Triangle Law Method: You can place the tail of at the head of . Then the resultant is the vector from the tail of to the head of . This method in your NCERT textbook is also referred to as the Head-to-Tail Method.
- Parallelogram Law: Let's place both vectors' tails at a common origin. That should form a parallelogram. The result here is the diagonal from the origin to the opposite vertex.
Properties of Vector Addition
- The result of the vector addition depends on the angle between the vectors.
- Vector addition is always commutative. Meaning, .
- Vector addition also follows the associative law. That is, (A+B) + C = A + (B+C)
- The maximum vector resultant occurs when vectors are parallel. The angle between the two vectors is 0 degree.
- The minimum vector resultant comes when vectors are anti-parallel. The angle then would be 180 degree.
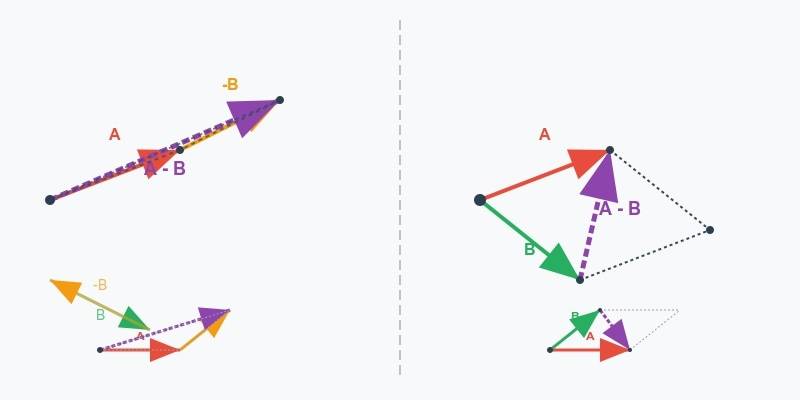
Vector Subtraction by Graphical Method
We use vector subtraction to find the difference between two vectors. We can represent this as the addition of one vector to the negative of another.
Same as above, let’s look at how we can use the triangle and parallelogram laws to subtract vectors.
What we need to consider here.
To find , compute , where has the same magnitude as but opposite direction.
- Graphically, we can place and tail-to-head (triangle law).
- Or, in a parallelogram, the difference is the diagonal from the head of to the head of resultant's magnitude and direction are measured geometrically.
Here is a graphical representation of vector subtraction using both these laws.
Properties of Vector Subtraction
- You should remember that vector subtraction is non-commutative:
- The negative vector always reverses direction.
- We typically use vector subtraction in relative motion problems.
- The difference vector points from the head of B to the head of A when both start from the same origin.
Applications of Addition and Subtraction of Vectors in Physics
Here are some applications where vector addition and subtraction using the graphical method are quite common.
Physics Applications
- We can easily determine the net force acting on various objects using vector addition and subtraction.
- Knowing the graphical methods with triangle and parallelogram laws helps in visualising how to merge velocities and accelerations for problem-solving
- Understanding how electric and magnetic fields interact
Engineering Applications
- With addition and subtraction of vectors, it’s easier to break down forces in trusses and frameworks
- Planning paths and coordinating arm movements in areas of robotics can be graphically represented with the addition or subtraction of vectors.
- Calculating navigation and trajectory paths is easier when using the graphical methods for vector
Everyday Applications
- For GPS navigation, we generally apply the same physics of displacement vectors to plan routes
- Even in areas of game development, professionals implement character movement and physics engines
- Vector addition and subtraction using the graphical method helps in analysing projectile motion in sports, such as ball games
JEE-Level Examples of Addition and Subtraction of Vectors
When you are preparing for JEE Main or similar tests, these are types of exercises you can practice. The solutions also have an additional concept, which you can read later in our guide to vector addition using the analytical method.
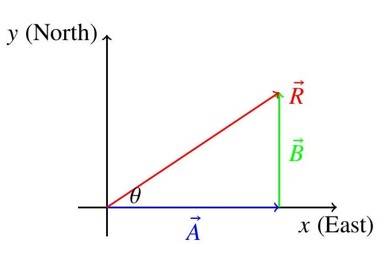
Example 1
Two displacements east and north are added. Sketch the resultant using the triangle law and estimate its magnitude and direction (scale: ).
Solution: Draw ( 3 cm east), then ( 4 cm north) from its head. The resultant is from the tail of to the head of .
Magnitude (measured): .
Direction (measured): north of east.
Analytical check: .
Diagram:
Diagram Description: Shows (blue) east, (green) north from 's head, and (red) from origin to 's head.
Example 2
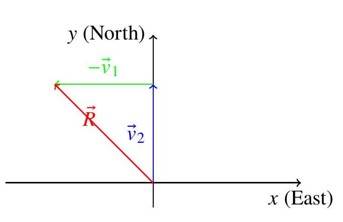
A velocity east is subtracted from north. Sketch (scale: ).
Solution: Compute as . Draw ( 4 cm north), then ( 4 cm west) from its head. Resultant is from tail of to head of .
Magnitude: .
Direction: north of west.
Analytical check: .
Diagram:
Diagram Description: Shows
(blue) north,
(green) west, and
(red) from origin to
's head.
Example 3
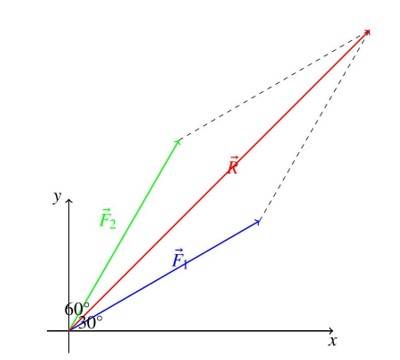
Add forces at to horizontal and at using parallelogram law (scale: ).
Solution: Draw at and at from a common origin, completing the parallelogram. The resultant is the diagonal.
Magnitude: .
Direction: to horizontal.
Analytical check: Angle between vectors , so .
Diagram:
Diagram Description: Shows (blue) at (green) at , a dashed parallelogram, and (red) as the diagonal.
Class 11 Physics Notes for Quick Revisions Before Exams
Stuck up before exams? Don't cram. Instead, go through these Physics chapter notes. Find topic-wise guides under each chapter too!
| Units and Measurements Class 11 Notes | Mechanical Properties of Solids Class 11 Notes |
| Motion in a Straight Line Class 11 Notes | Mechanical Properties of Fluids Class 11 Notes |
| NCERT Class 11 Notes for Motion in a Plane | Thermal Properties of Matter Class 11 Notes |
| Laws of Motion Class 11 Notes | Thermodynamics Class 11 Notes |
| Work, Energy, and Power Class 11 Notes | Kinetic Theory of Gas Class 11 Notes |
| System of Particles and Rotational Motion Class 11 Notes | Oscillations Class 11 Notes |
| Gravitation Class 11 Notes | Waves Class 11 Notes |
Some more Science stream notes for Class 11 CBSE to check.
| NCERT Class 11 Notes for PCM |
| NCERT Class 11 Physics Notes |
NCERT Solutions for Class 11 Physics Simplified
Commonly asked questions
Why can't a vector be added by simple algebra?
Scalar quantities only have magnitude, which makes sense to combine using ordinary algebra. But vector quantities have both magnitude and direction. Due to this directional aspect, vectors must obey special rules of vector algebra. Vectors have to specifically follow the triangle law or the parallelogram law of addition to be represented in the graph format. These graphical methods account for both magnitude and direction. This makes sure that the resultant vector accurately reflects the combined effect of the individual vectors. If we apply ordinary algebra, we won't be able to know the directional information.
How reliable is the graphical method for vector addition and subtraction?
The graphical method using the head-to-tail or parallelogram laws only helps in visualising vectors and their resultants. But, it has limited accuracy. Because they cannot be precise when you consider the scale and angles. That's why it is important to use vector addition using the analytical method. That involves combining vector components. The graphical approach is primarily for conceptual understanding.
How to find direction in vector subtraction?
To find the direction in vector subtraction, let's consider (A – B). We have to use vector addition by rewriting it as A + (–B). Then, this negative vector (–B) will have the same magnitude as B. Only that it will point in the opposite direction. Then we will use the head-to-tail method. Following that, we will place the tail of (–B) at the head of A. The resultant vector from the tail of A to the head of –B will give us both the magnitude and direction of A – B.
Physics Motion in Plane Exam
Student Forum
Other Class 11th Physics Chapters
- Physics Mechanical Properties of Solids
- NCERT Class 11 Physics
- NCERT Class 11 Notes
- NCERT Notes
- Physics Motion in Plane
- Physics Mechanical Properties of Fluids
- Physics Motion in Straight Line
- Physics System of Particles and Rotational Motion
- Physics Oscillations
- Physics Waves
- Physics Thermal Properties of Matter
- Physics Motion
- Physics Gravitation
- Physics Thermodynamics
- Physics Work, Energy and Power
- Physics Units and Measurement
- Physics Laws of Motion