The graphical method for vector addition and subtraction is not always accurate. If you’ve gone through the concept of vector resolution, the next thing to learn is the analytical method for adding vectors. This method focuses on combining two or more vectors to form a single resultant vector. That shows the net effect. It’s also much more accurate, as it combines trigonometry and geometry to calculate the magnitude and direction.
- Vector Addition using Analytical Method
- Vector Addition Formula
- Procedure for Analytical Method for Vector Addition
- Example of Vector Addition Formula
- Sample JEE-Style Examples for Vector Addition using Analytical Method
- Revise Physics Class 11 Chapters and Topics
- Find Expert-Written NCERT Solutions for Class 11 Physics
Vector Addition using Analytical Method
The analytical method of vector addition resolves vectors into components along coordinate axes, sums the components, and shows the resultant vector's magnitude and direction. This addition, which you may recall from early in the Motion in a Plane 11 notes, either follows the parallelogram or triangle law.
Importance of Vector Addition using the Analytical Method
Here are some essentials to help you understand why vector addition is important when using the analytical method.
- It applies to any number of vectors.
- Complex geometric problems can be simplified into algebraic ones.
- Essential for equilibrium problems (net force =0).
- Used in navigation and kinematics problems.
Learning about vector addition using the analytical method is also essential for the JEE Main.
In case you missed it, check out our article on scalar and vector quantities.
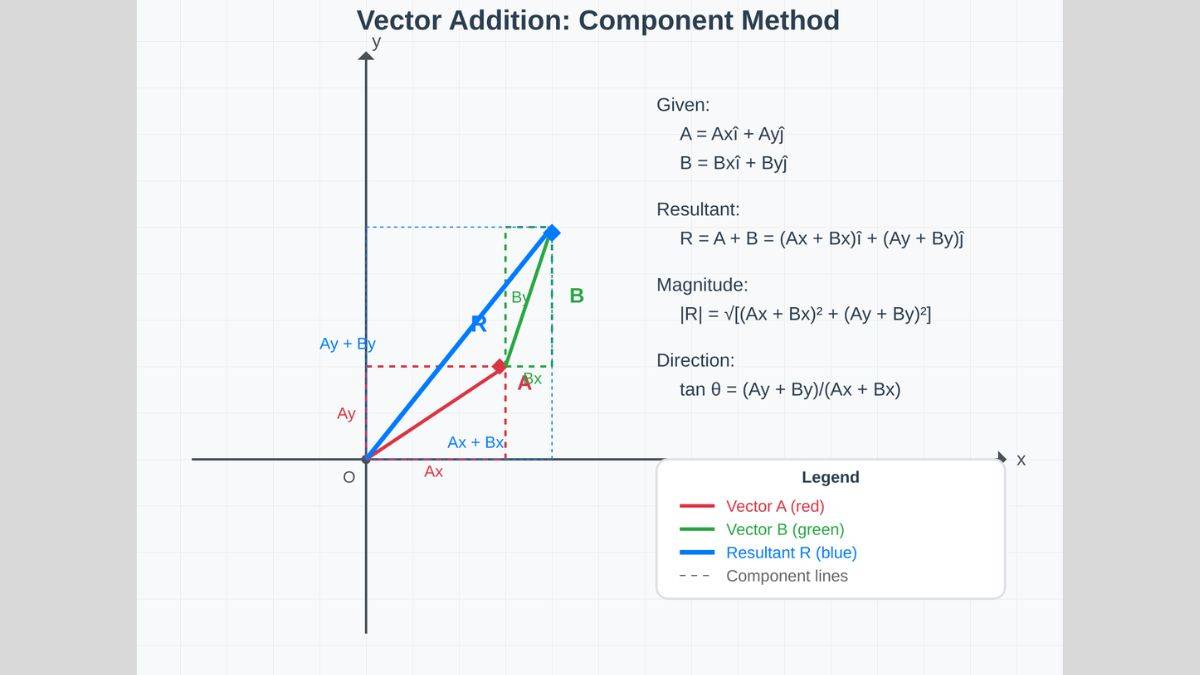
Vector Addition Formula
For vectors and , the resultant is found by resolving each into components along and axes.
If , then:
Magnitude: .
Direction: .
Procedure for Analytical Method for Vector Addition
The analytical method involves resolving vectors into components, summing them, and reconstructing the resultant vector.
- You can resolve each vector into - and -components using .
- After vector resolution, the next step is to sum the components .
- Then we compute the resultant magnitude .
- After that, we can find the direction using . This will help adjust the correct quadrant.
Example of Vector Addition Formula
Let's say, you take a walk of 3 metres in the east direction. Then you go up 4 metres north.
The displacement components in the situation are (3,4).
The total displacement magnitude is √(3² + 4²) = 5 metres at an angle of tan⁻¹(4/3) ≈ 53° north of east.
You know this component method works only because vectors follow the parallelogram rule.
To illustrate how we apply the vector addition formula for two displacement vectors, consider the following snapshot.
Vector A (walking east): A = 3î + 0ĵ
Ax = 3, Ay = 0
Vector B (walking north): B = 0î + 4ĵ
Bx = 0, By = 4
Using the vector addition formula:
Resultant R = A + B:
Rx = Ax + Bx = 3 + 0 = 3
Ry = Ay + By = 0 + 4 = 4
So R = 3î + 4ĵ
Magnitude:
|R| = √[(Ax + Bx)² + (Ay + By)²] = √(3² + 4²) = √(9 + 16) = √25 = 5 meters
Direction:
θ = tan⁻¹[(Ay + By)/(Ax + Bx)] = tan⁻¹(4/3) ≈ 53° north of east
The formula gives us the net displacement: instead of walking 7 meters total (3 + 4), you end up 5 meters from your starting point in a straight line.
Sample JEE-Style Examples for Vector Addition using Analytical Method
Here are some sample exercises to practice when you are preparing for competitive tests.
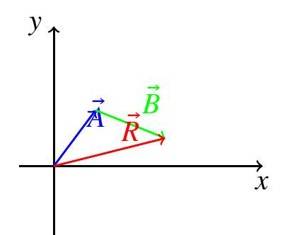
Example 1: Two vectors and represent displacements. Find the resultant displacement's magnitude and direction.
Solution:
Magnitude: . Direction: , so (first quadrant).
Diagram:
Diagram Description: The diagram shows (blue), (green) added head-to-tail, and resultant (red) from origin to the tip of .
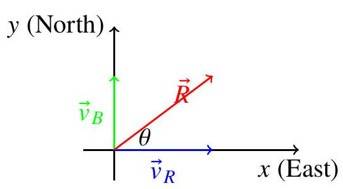
Example 2: A boat moves at north, and the river flows at east. Find the boat's resultant velocity relative to the ground.
Solution: Boat: . River: .
Magnitude: . Direction: , so north of east.
Diagram:
Diagram Description: The diagram shows
(blue) along east,
(green) along north, and resultant
(red) at angle
.
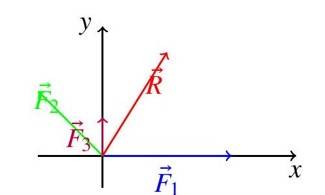
Example 3: Three forces act on a particle: . Find the net force.
Solution:
Magnitude: N. Direction: , so .
Diagram:
Diagram Description: The diagram shows (blue), (green), (purple), and resultant (red) summed head-to-tail.
Revise Physics Class 11 Chapters and Topics
Check out these links to revise all your Physics chapters easily before exams.
| Units and Measurements Class 11 Notes | Mechanical Properties of Solids Class 11 Notes |
| Motion in a Straight Line Class 11 Notes | Mechanical Properties of Fluids Class 11 Notes |
| NCERT Class 11 Notes for Motion in a Plane | Thermal Properties of Matter Class 11 Notes |
| Laws of Motion Class 11 Notes | Thermodynamics Class 11 Notes |
| Work, Energy, and Power Class 11 Notes | Kinetic Theory of Gas Class 11 Notes |
| System of Particles and Rotational Motion Class 11 Notes | Oscillations Class 11 Notes |
| Gravitation Class 11 Notes | Waves Class 11 Notes |
Some more Science stream notes for Class 11 CBSE to check.
| NCERT Class 11 Notes for PCM |
| NCERT Class 11 Physics Notes |
Find Expert-Written NCERT Solutions for Class 11 Physics
Find the NCERT Solutions for all the chapters in Class 11 right here.
Keep exploring the regularly updated NCERT Solutions for Physics Class 11!
Commonly asked questions
What is the analytical treatment of triangle law of vector addition?
It resolves vectors into components, adds corresponding x and y values algebraically, then reconstructs the resultant using magnitude and direction. That is, applying vector addition rules.
How are vectors added graphically and analytically?
Graphically, we place vectors head-to-tail. Analytically, we add components along axes using coordinate geometry, trigonometric functions, and unit vectors for precise vector resultant calculation.
Physics Motion in Plane Exam
Student Forum
Other Class 11th Physics Chapters
- Physics Mechanical Properties of Solids
- NCERT Class 11 Physics
- NCERT Class 11 Notes
- NCERT Notes
- Physics Motion in Plane
- Physics Mechanical Properties of Fluids
- Physics Motion in Straight Line
- Physics System of Particles and Rotational Motion
- Physics Oscillations
- Physics Waves
- Physics Thermal Properties of Matter
- Physics Motion
- Physics Gravitation
- Physics Thermodynamics
- Physics Work, Energy and Power
- Physics Units and Measurement
- Physics Laws of Motion