Resolution of Vectors: Components, Diagram, Applications

Vector resolution is the process of breaking down a vector into two or more components and laying them out in a 2D plane. The sum of these smaller vector components is always equal to the original vector.

Here is an example of the resolution of a vector in mathematical terms. 

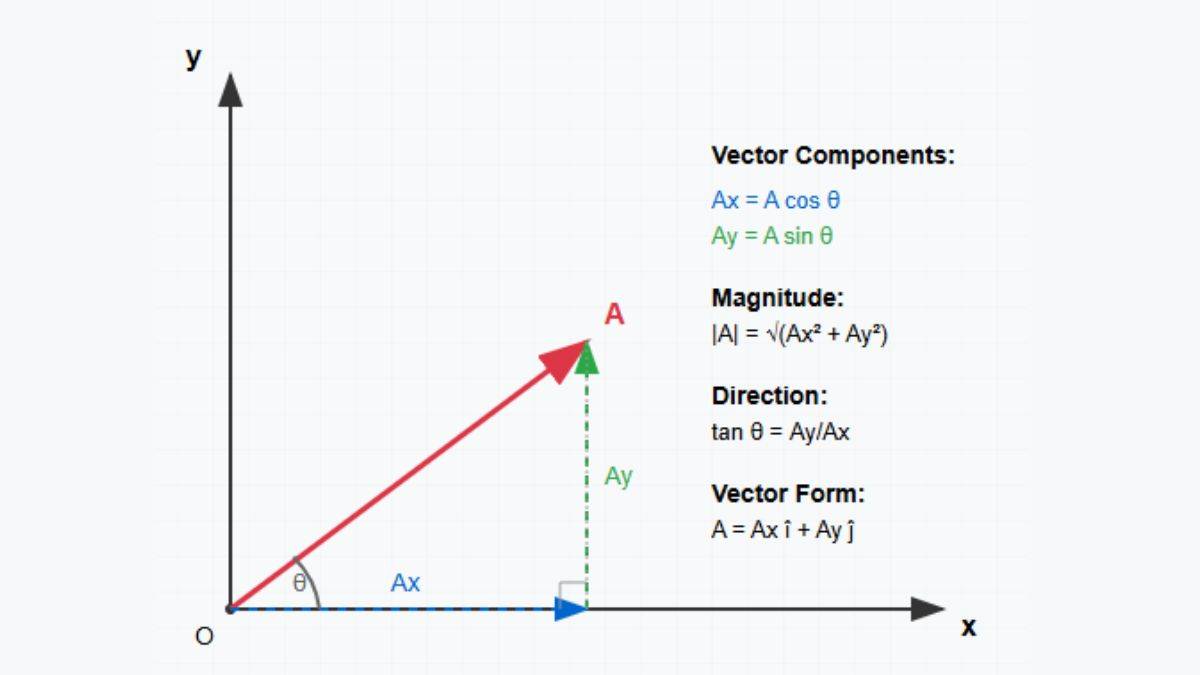
A vector $\vec{A}$  in the $x-y$ plane can be resolved into components $A_x\hat{i}+A_y\hat{j}$ .

Here , $A_x=A\mathrm{c}\mathrm{o}\mathrm{s}\theta ,A_y=A\mathrm{s}\mathrm{i}\mathrm{n}\theta$ and $\theta$  is the angle with the positive $x$ -axis. The magnitude is $\left|\vec{A}\right|=\sqrt[]{A_x^2+A_y^2}$ , and the direction is $\mathrm{t}\mathrm{a}\mathrm{n}\theta =\frac{A_y}{A_x}$ .

What this image is saying. 

• Vector Components: A 2D vector is the sum of its horizontal (x) and vertical (y) parts. Axiˆ+Ayjˆ
• Calculating Components: The x-component is A⋅cos(θ) and the y-component is A⋅sin(θ).
• Calculating Magnitude: The vector's length (magnitude) is found using the Pythagorean theorem on its components.
• Calculating Direction: The vector's angle is found from the ratio of its y-component to its x-component.

Key Features of the Resolution of Vectors

• Vector components depend on the chosen coordinate system.
• The perpendicular components of the single vector, after breaking them down, are independent. This helps in analysing motion in a 2D or 3D plane.
• Vector resolution preserves the vector's magnitude and direction.

In two dimensions or a 2D plane, a vector is typically resolved along the $x$  - and $y$ -axes. That enables us to analyse each component independently. 
Let’s consider this example. 
For a vector $\vec{A}$  making angle $\theta$ with the $x$ -axis, components are

$A_x=A\mathrm{c}\mathrm{o}\mathrm{s}\theta ,\mathrm{}{A}_y=A\mathrm{s}\mathrm{i}\mathrm{n}\theta$

In motion in a plane, velocity $\vec{v}=v_x\hat{i}+v_y\hat{j}$  is resolved similarly.

For example, in projectile motion, initial velocity $\vec{u}$  at angle $\theta$  has components $u_x=u\mathrm{c}\mathrm{o}\mathrm{s}\theta$ , $u_y=u\mathrm{s}\mathrm{i}\mathrm{n}\theta$ .

Key Observations

• Horizontal component $A_x$ is the projection along $x$ -axis.
• Vertical component $A_y$ is the projection along $y$ -axis.
• Components can be positive or negative based on direction.

Horizontal Component of Vectors

The horizontal component in physics is a force component that moves along the x-axis, in parallel. 

Vertical Component of Vectors

This vector component in the resolution of vectors is required to understand the force component that lies perpendicular to the x-axis. 

You can resolve vectors along any pair of axes. It does not necessarily have to be Cartesian. What that means is, these vectors do not have to be along an inclined plane or radial/tangential directions.

Then, when you consider projectile motion on an inclined plane, the coordinate system usually aligns with the incline ( $x$ -axis) and perpendicular to it ( $y$ -axis).

For a projectile launched at angle $\theta$ relative to the incline of angle $\alpha$ , velocity components are $u_x=u\mathrm{c}\mathrm{o}\mathrm{s}(\theta -\alpha ),u_y=u\mathrm{s}\mathrm{i}\mathrm{n}(\theta -\alpha )$ for motion up the incline

Key Observations

• Choice of axes simplifies equations (e.g., along incline reduces acceleration components).
• Acceleration components adjust based on the coordinate system (e.g., $a_x=-g\mathrm{s}\mathrm{i}\mathrm{n}\alpha$ ).

 

Vector resolution applies to motion anywhere. It can be used to analyse common forces, velocities, and displacements in kinematics, dynamics, and relative motion. 

1. Basic Projectile Motion: Vector resolution is performed by breaking down the initial velocity into horizontal and vertical components to determine range, time of flight, and height. Take, for example, a thrown ball motion. The only force here is gravity, which does not affect any sideways motion. So we split the initial velocity into a horizontal component (Vx) and a vertical component (Vy). Vx tells you the ball's range (how far it goes). Vy tells you its maximum height and how long it is in the air.
2. Relative Motion: Resolving velocities to find relative velocity. Let’s take an example of the boat's velocity relative to a river. The boat's final path is a combination of its own effort and the river's push. We resolve the boat's velocity and the river's velocity into components. They are across-stream and downstream here. We can add the across-stream component to the downstream one. That gives the boat's true diagonal path and speed.
3. Circular Motion: Resolving velocity into radial and tangential components, with centripetal acceleration along the radius. Let’s consider a car turning a corner. The force that makes the car turn is always pointed towards the centre of the circle. It’s also perpendicular to its direction of travel. We resolve the object's acceleration into a radial (inward) component and a tangential (forward) component.

Here are a few basic examples for JEE Main questions you can prepare. Before these, you also might look into the NCERT Solutions for Chapter 3.

Example 1: A velocity vector $\vec{v}=20\mathrm{m}/\mathrm{s}$  makes a ${30}^{\circ }$  angle with the horizontal. Find its components along the $x$ - and $y$ -axes. 

$v_x=v\mathrm{c}\mathrm{o}\mathrm{s}\theta =20\mathrm{c}\mathrm{o}\mathrm{s}{30}^{\circ }=20\cdot \frac{\sqrt[]{3}}{2}=10\sqrt[]{3}\mathrm{m}/\mathrm{s},\mathrm{}{v}_y=v\mathrm{s}\mathrm{i}\mathrm{n}{30}^{\circ }=20\cdot \frac{1}{2}=10\mathrm{m}/\mathrm{s}$

Example 2: A projectile is launched at $50\mathrm{m}/\mathrm{s}$  at ${60}^{\circ }$  from the horizontal. Find the horizontal and vertical components of velocity after $2\mathrm{s}\left(g=10\mathrm{m}/{\mathrm{s}}^2\right)$ .

Initial components: $u_x=50\mathrm{c}\mathrm{o}\mathrm{s}{60}^{\circ }=25\mathrm{m}/\mathrm{s},u_y=50\mathrm{s}\mathrm{i}\mathrm{n}{60}^{\circ }=25\sqrt[]{3}\mathrm{m}/\mathrm{s}$ .

Horizontal: $v_x=u_x=$ $25\mathrm{m}/\mathrm{s}$    (no acceleration).

Vertical: $v_y=u_y-gt=25\sqrt[]{3}-10\cdot 2=25\sqrt[]{3}-20\approx 23.3\mathrm{m}/\mathrm{s}$ .

Example 3: A boat sails at $4\mathrm{m}/\mathrm{s}$  perpendicular to a river flowing at $3\mathrm{m}/\mathrm{s}$ . Find the velocity components relative to the ground.

Boat's velocity: ${\vec{v}}_{AB}=4\hat{j}$ ,

River's velocity: ${\vec{v}}_B=3\hat{i}$ .

Resultant: . Components: $v_x=3\mathrm{m}/\mathrm{s},v_y=4\mathrm{m}/\mathrm{s}$ .

Go through these Physics chapter notes for Class 11. Find topic-wise guides for each. 

Units and Measurements Class 11 Notes	Mechanical Properties of Solids Class 11 Notes
Motion in a Straight Line Class 11 Notes	Mechanical Properties of Fluids Class 11 Notes
NCERT Class 11 Notes for Motion in a Plane	Thermal Properties of Matter Class 11 Notes
Laws of Motion Class 11 Notes	Thermodynamics Class 11 Notes
Work, Energy, and Power Class 11 Notes	Kinetic Theory of Gas Class 11 Notes
System of Particles and Rotational Motion Class 11 Notes	Oscillations Class 11 Notes
Gravitation Class 11 Notes	Waves Class 11 Notes

Some more Science stream notes for Class 11 CBSE to check.

NCERT Class 11 Notes for PCM

NCERT Class 11 Physics Notes

 

Find the NCERT Solutions for all the chapters in Class 11 below.  

Units and Measurements Class 11 NCERT Solutions	Mechanical Properties of Solids Class 11 NCERT Solutions
Motion in a Straight Line Class 11 NCERT Solutions	Mechanical Properties of Fluids Class 11 NCERT Solutions
Motion in a Plane Class 11 NCERT Solutions	Thermal Properties of Matter Class 11 NCERT Solutions
Laws of Motion Class 11 NCERT Solutions	Thermodynamics Class 11 NCERT Solutions
Work, Energy, and Power Class 11 NCERT Solutions	Kinetic Theory Class 11 NCERT Solutions
System of Particles and Rotational Motion Class 11 NCERT Solutions	Oscillations Class 11 NCERT Solutions
Gravitation Class 11 NCERT Solutions	Waves Class 11 NCERT Solutions

Keep exploring the regularly updated NCERT Solutions for Physics Class 11!