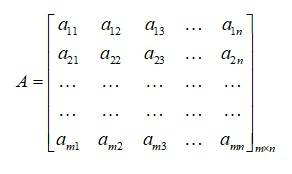There are various ways to arrange or represent numbers, objects, and other elements in mathematical form. One of these ways is the Matrix. Matrix is one of the most used methods to make complex calculations easy and less time taking.
A matrix is a representation of various variables in rows and columns in a rectangular array. You can picture this array as a table without the grid lines. The plural form of Matrix is Matrices.
Class 12 Maths chapter 5 deals with Matrices. This chapter includes fundamental concepts, including order, types of matrices, and algebraic operations of matrices. These short revision notes of class 12 matrices are also available in a downloadable PDF for free.
The Class 12 Matrices Notes cover all the concepts related to matrices and their properties. These NCERT Notes are best for CBSE exams and JEE exams for Matrices revision. You can use our NCERT Solutions for Matrices to practice the questions and strengthen your grasp. Read the article below.
- What is Matrix (Matrices)
- Order of a Matrix
- Type of Matrices
- Operation of Matrices
- Addition of Matrices
- Properties of Matrix Addition
- Subtraction of Matrices
- Scalar Multiplication (Multiplication of a Matrix by a Scalar)
- Multiplication of Matrices
- Properties of Matrix Multiplication
- Important Facts related to Matrices for CBSE, and JEE Mains
What is Matrix (Matrices)
Suppose Ram is visiting a fair with his children: Raman, John, and Durga. They bought 3 toys: Cars, Trucks, and Bikes, each in a different quantity.
| Variables |
Car |
Truck |
Bike |
|---|---|---|---|
| Raman |
2 |
0 |
0 |
| John |
0 |
1 |
0 |
| Durga |
0 |
0 |
3 |
The above table is a way to represent the data in the above word problem in mathematical form. Similarly, a Matrix is a method to display this data; this light green part of the table can be represented in a matrix.
A =
According to the NCERT definition, “A matrix is an ordered rectangular array of numbers or functions. The numbers or functions are called the elements or the entries of the matrix.”
The values/functions in the matrices are called elements, such as the number of toys in the above matrix are elements. The vertical line of elements is called a column, and the horizontal line of elements is called a row. The above example has 3 columns and 3 rows.
Order of a Matrix
If a matrix has m rows and n columns, the matrix will be called a matrix. The order of the matrix is . The matrix of order is displayed below.
In concise form, the Matrix is also represented as , where , .
The element in position is denoted as element, where i represents row and j represents column.
Type of Matrices
There are various types of matrices based on different factors, including resultant, elements, and other properties. Read types of matrices below.
| Matrix |
Property |
| Zero Matrix |
All the elements must be 0. |
| Row Matrix |
A matrix which have only a single row. |
| Column Matrix |
A matrix which have only a single column. |
| Square Matrix |
The number of columns must be equal to the number of rows. |
| Identity Matrix |
All the diagonal elements are 1. |
| Scaler Matrix |
All diagonal elements are equal. |
| Diagonal Matrix |
All other elements are zero except the diagonal elements. |
| Symmetric Matrix |
A square matrix where A = AT (T is the transpose of A) |
| Singular Matrix |
The modulus of the matrix is zero. |
| Non-singular Matrix |
The modulus of the matrix is not zero. |
Operation of Matrices
There are specific ways to perform basic mathematical operations like addition, subtraction, and multiplication of matrices. You can check important Matrix operations below:
- Addition of Matrices
- Subtraction of Matrices
- Multiplication of a Matrix by a Scalar
- Multiplication of Matrices
Read the detailed version of these operations of matrices below:
Addition of Matrices
Matrices are added by the sum of each corresponding element. If there are two matrices A and B, such that, and are two matrices of the same order.
Sum of matrices A and B (adding each corresponding element):
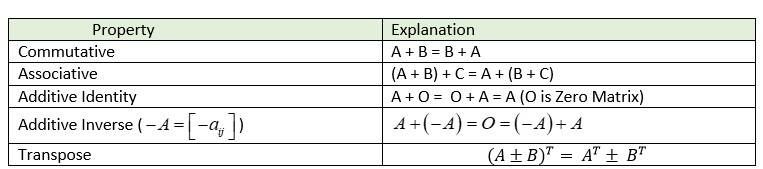
Properties of Matrix Addition
If there are three different matrices A, B, and C of the same order. The properties of the addition of matrices are given below:
Note Points:
- Two matrices must be of the same order to be added or subtracted. The addition of matrices is only defined for the same order.
- For every matrix, there exists an additive inverse matrix such that . Where is the additive inverse of the matrix A.
Subtraction of Matrices
The subtraction of matrices follows almost same set of rules as addition. If and are two matrices of the same order, then difference of matrices A and B will be: .
- Subtraction of matrices does not commutative and associative properties as addition.
- is a matrix obtained by subtracting the elements of B from the corresponding elements of A.
Scalar Multiplication (Multiplication of a Matrix by a Scalar)
Multiplication of Matrices
Properties of Matrix Multiplication
Important Facts related to Matrices for CBSE, and JEE Mains
Maths Matrices Exam
Student Forum
Other Class 12th Maths Chapters
- Quantitative Aptitude Prep Tips for MBA
- Maths Integrals
- Maths Differential Equations
- Maths Vector Algebra
- Maths Matrices
- Maths Determinants
- Maths Inverse Trigonometric Functions
- Maths Differentiation
- NCERT Class 12 Maths
- Maths Continuity and Differentiability
- Maths Applications of Derivatives
- Maths Application of Integrals
- Maths Linear Programming
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test