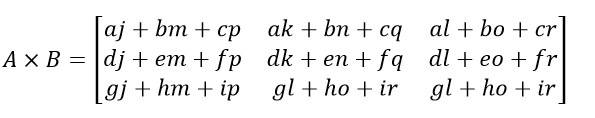Let R 1 = { ( a , b ) ∈ N × N : | a − b | ≤ 1 3 } a n d  R 2 =  { ( a , b ) ∈ N × N : | a − b | ≠ 1 3 } . Then on N :

Neither R 1 nor R 2 is an equivalence relation

Both R 1 and R 2 are equivalence relations

R 1 is an equivalence relation but R 2 is not

R 2 is an equivalence relation but R 1 is not

Operations on Matrices: Overview, Questions, Preparation

Updated on Aug 11, 2025 13:21 IST

By nitesh singh, Senior Executive

There are various mathematical calculations going on behind the curtain, such as how a 3D game renders realistic movements, predicting weather patterns and many more. The hero of making these large calculations easy as cake is matrix operations. What is matrix and its operation? In this article, we will discuss in detail.

A matrix is a rectangular array of elements or numbers. Matrices are used to simplify calculations for various types of algebraic operations. You can use matrices to solve systems of linear equations and coordinate geometry problems. However, you must have a clear understanding of the operations of matrices.

Matrix operations consist of addition, subtraction, multiplication by a scalar, and matrix multiplication. In our NCERT Notes for this and other matrix concepts, we have discussed the properties of matrix operations in detail. You can also download the matrix operations short note PDF for free here. Read this article below;

Table of content

Operations on Matrix :Overview
Addition of Matrices
Properties of Matrix Addition
Subtraction of Matrices
Properties of Matrix Subtraction
Scalar Multiplication of Matrices
Properties of Scalar Multiplication
Multiplication of Matrices (Cross Product)
Properties of Matrix Multiplication
Tips for Competitive Exam Preparation
Complete Class 11 Study Material

Operations on Matrix :Overview

Like we have rules for algebraic operations, Matrix operations also consist of specific rules. There are specific rules for addition, subtraction, and multiplication related to row, column, and order of the matrix. There are four basic operations of matrices:

Addition of Matrices
Subtraction of Matrices
Scalar Multiplication of Matrices
Multiplication of Matrices

These properties are a must for all CBSE and competitive exam students. You can take the help of these properties to practice the NCERT Solutions of Matrices and master the problem-solving for this chapter. Check matrix operations in detail below.

Addition of Matrices

In matrix addition, every element is added to the corresponding element of the other matrices. It is very important to note that matrices must be of the same order to be added or subtracted. You can check the mathematical representation for the addition of matrices:

Suppose, $A = [a_{i j}]$ and $B = [b_{i j}]$ are two matrices, then C = A+B

$\Rightarrow c_{i j} = a_{i j} + b_{i j}$

For example, If $A = [\begin{matrix} a & b & c \\ d & e & f \\ g & h & i \end{matrix}]$ and $B = [\begin{matrix} j & k & l \\ m & n & o \\ p & q & r \end{matrix}]$

Then, $A + B = [\begin{matrix} a + j & b + k & c + l \\ d + m & e + n & f + 0 \\ g + p & h + q & i + r \end{matrix}]$

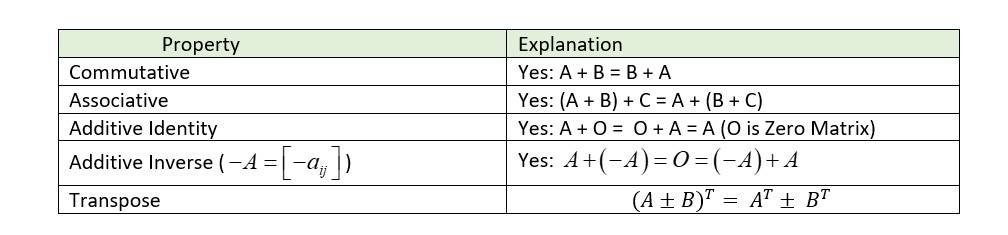
Properties of Matrix Addition

If there are three different matrices A, B, and C of the same order. The properties of the addition of matrices are given below:

Subtraction of Matrices

Subtraction also follows the same principle as addition. To add two or more matrices, the order of all the matrices must be the same. The corresponding elements will be subtracted to get the answer. In mathematical terms, if there are two matrices, $A = [a_{i j}]$ and $B = [b_{i j}]$ , the difference two matrices C =A – B, Then

$\Rightarrow c_{i j} = a_{i j} + b_{i j}$

For example, If $A = [\begin{matrix} a & b & c \\ d & e & f \\ g & h & i \end{matrix}]$ and $B = [\begin{matrix} j & k & l \\ m & n & o \\ p & q & r \end{matrix}]$

Then, $A - B = [\begin{matrix} a - j & b - k & c - l \\ d - m & e - n & f - 0 \\ g - p & h - q & i - r \end{matrix}]$

Subtraction of matrices does not have commutative and associative properties like addition.

$A - B$ is a matrix obtained by subtracting the elements of B from the corresponding elements of A.

Properties of Matrix Subtraction

Scalar Multiplication of Matrices

Scalar multiplication is the simplest of all the operations of a matrix. Like algebraic multiplication, you just need to multiply each element of the matrix by the same scalar (Constant) quantity or number. You can understand the process through the example below

For Example, If, $A = [\begin{matrix} a & b & c \\ d & e & f \\ g & h & i \end{matrix}]$ it is multiplied by k.

Then, it will be $k.A = [\begin{matrix} ak & bk & ck \\ dk & ek & fk \\ gk & hk & ik \end{matrix}]$

Properties of Scalar Multiplication

The scalar multiplication operation on matrices has the following properties:

$k (A + B) = k A + k B; Distributive$
$(k + l) A = k A + l A; Distrubutive$

Multiplication of Matrices (Cross Product)

The multiplication of two matrices is not the same as algebraic multiplication. If there are two matrices, then the row (horizontal) of the matrix will be multiplied by the respective column to get the required element. Let’s assume there are two matrices $A = [a_{i j}]$ and $B = [b_{i j,}]$ respectively of order m x n and n x p, and $A \times B = C$ .

Then $\Rightarrow c_{i j} = \sum (a_{i k} . b_{k j})$

For Example, if $A = [\begin{matrix} a & b & c \\ d & e & f \\ g & h & i \end{matrix}]$ and $B = [\begin{matrix} j & k & l \\ m & n & o \\ p & q & r \end{matrix}]$

Then,

NOTE: To multiply two different matrices, the number of columns in the first matrix must be equal to the number of rows in the second matrix.

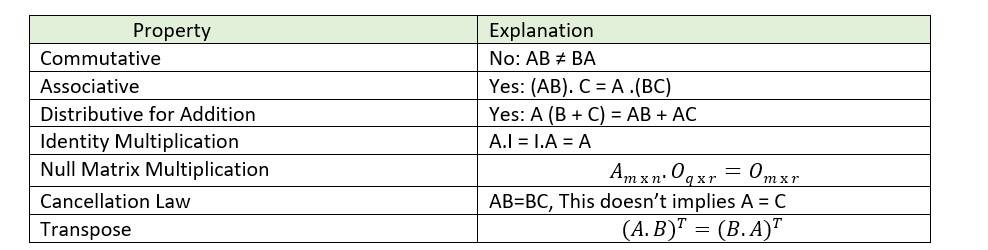
Properties of Matrix Multiplication

Matrix Multiplication is associative. For any three matrices A, B and C, we have (AB)C = A(BC), whenever both sides of the equality are defined.
Matrix Multiplication is distributive over matrix addition. For any three matrices A, B and C, we have A (B + C) = AB + AC and (A + B) C = AC + BC, whenever both sides of the equality are defined.
Existence of Multiplicative Identity. For every square matrix A, there exists an identity matrix of same order such that IA = AI = A.
Matrix Multiplication is not commutative in general. For any two matrices A and B, if both AB and BA are defined, it is not necessary that AB = BA. (i.e. Commutativity may hold in some cases, but may not hold in some other.)
Zero matrix as the product of two non–zero matrices

You can read the properties in summarized format below.

Tips for Competitive Exam Preparation

Here are a few important points that can be extremely useful to get the results quickly and avoid errors while solving the problem in JEE or other competitive exams.

Before adding or subtracting two or more matrices, you must check the order of both matrices; only if they are of the same order, then proceed to add or subtract.
For multiplication, the number of columns in the first matrix must be equal to the rows in the second matrix. If not, you can’t multiply those two matrices.
If two matrices are equal to each other, you can find the values of variables by comparing the corresponding elements.
If two matrices A and B of m x n and n x p orders, respectively. The product AB matrix of m x p order.
The transpose of a matrix (denoted as A') is obtained by swapping its rows and columns of the original matrix.